非参特征变换在分类问题中的研究及应用
严 红,刘云霞
(厦门大学 经济学院,福建 厦门 361005)
从海量、复杂的数据中提取有用信息是当前大数据背景下的一个主要任务。复杂数据常呈现出高维、结构复杂及不同类相互重叠、非线性可分的特点。传统的分类方法在非线性可分数据面前往往失效。考虑到分类问题是数据分析的主要问题,文本、图像和异常检测等领域中的许多问题都是基于分类展开分析的。因此,本文将在半朴素贝叶斯分类思想的基础上,引入一元和二元核密度估计进行非参特征变换以解决非线性可分数据二分类及多分类的问题。
一、文献综述
分类问题中常会出现不同类别重叠、非线性可分的情况。国内外的学者均提出了一些方法用于解决该问题。Vaidyanathan等发现染色体的分类是非线性可分的,由此提出一种基于非线性决策边界的分类器解决这一问题[1]。Shams结合核主成分分析提出了一种异常检测方法,用于解决异常检测领域中经常出现的非线性可分问题[2]。Aronov等针对二分类问题提出了一种最小化线性分类器分类误差的方法,指出通过最小化分类误差可以用线性分类器解决非线性可分的问题[3]。周志华根据前人的研究文献指出,在非线性可分的情况下,支持向量机通过引入核函数,将数据从低维空间映射到高维空间,从而达到较好的分类效果[4]。Fan等针对线性分类方法不能有效处理非线性可分的问题,提出用核密度估计方法对原始数据进行特征变换,在变换后的特征空间中进行分类的方法[5]。可见,利用非参数的相关方法解决非线性可分的分类问题是目前较为有效的方法。其中,基于核密度估计的非参特征变换方法在这方面的表现更为突出,但相关文献中采用的多是一元核密度估计的形式,因而没有考虑特征之间的相关性。
解决特征之间相关性的问题,可以基于半朴素贝叶斯的思想进行。半朴素贝叶斯分类器(Semi-Naïve Bayesian Classifier)放松了朴素贝叶斯分类器特征独立的假设,在计算后验概率时考虑特征之间的相关性。Kononenko指出,当特征之间有较强的相关性时,朴素贝叶斯分类器不再适用,由此提出半朴素贝叶斯分类器[6]。Friedman等研究了基于贝叶斯网络的分类器,提出通过树结构改进朴素贝叶斯分类器,并把这种方法称为TAN(Tree Augmented Naive Bayes)[7]。Keogh等基于TAN方法中“父特征”的概念提出了“超父”(Super-Parent),即除类别外所有特征都依赖于同一个特征,这种方法被称为SPODE(Super-Parent One-Dependent Estimator)[8]。Webb等发现SPODE方法在计算过程中需要寻找超父特征,模型的复杂度高,不利于计算,从而提出了AODE(Averaged One-Dependent Estimator)方法[9]。Yang等在对比了逐步选择、交叉验证、AODE等方法后发现AODE方法更有效[10]。Jiang等指出AODE分别将每个特征作为超父构建SPODE,将多个SPODE进行平均时,对每个SPODE都赋予相同的权重并不合适,据此他们提出了WAODE(Weighted Averaged One-Dependent Estimator),并给出了四种不同的加权方法[11]。由于WAODE依赖于加权方法的选择,分类效果并不稳定,所以采用AODE方法的思想引入二元核密度估计来刻画变量间的相关性更为适合。
关于非线性可分的多分类问题,现有文献常是以二分类问题为起点,再考虑多分类问题。Friedman提出了One-vs-One的分类思想,即对多个类别两两建立二分类模型,将每个测试样本都用多个二分类模型进行分类[12]。Hsu等通过比较发现One-vs-One和有向无环图的方法在实际多分类问题中更有效[13]。Lorena等指出从二分类问题到多分类问题主要有两种策略,一是修改二分类方法的目标函数使之适用于多分类,二是将多分类问题分解成多个二分类问题[14]。Galar等将One-vs-One和One-vs-All两种方法分别与SVM、决策树、kNN等分类方法结合用于解决多分类问题,他们发现One-vs-One的效果比One-vs-All更好[15]。
基于非线性可分数据的特点及相关文献梳理,本文认为可以从二分类问题开始,通过一元核密度估计和二元核密度估计对原变量进行特征变换,将得到的新变量用于构建决策边界的模型。这样,既保留了原始变量的信息,也考虑了变量间的相关性。而后,通过One-vs-One的方法将上述的二分类方法扩展成多分类方法,从而解决多分类类间重叠、非线性可分等问题。
二、方法介绍
(一)基于一元核密度估计的二分类方法
Fan等提出了一种用于解决二分类问题的方法[5]。该方法在分类过程中,采用核密度估计进行特征变换,并在模型中加入了Lasso惩罚项进行变量选择。他们把这种方法称作Feature Augmentation via Nonparametrics and Selection,简称FANS。
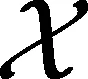
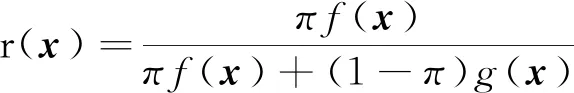
(1)

{x:f(x)/g(x)=1}={x:logf(x)-logg(x)=0}
(2)
根据朴素贝叶斯分类器的假设,当给定类别标签时,各个特征相互独立,有:
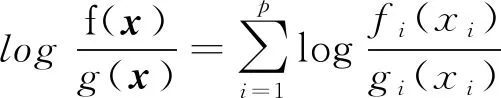
(3)
其中,fi(xi)和gi(xi)分别是在给定类别为1和给定类别为0的条件下变量xi对应的概率密度函数。
基于此,先估计每个变量的核密度函数,再用核密度函数之比进行特征变换,然后利用新变量建立Logistic回归模型。具体的决策边界可以表示为:
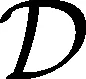
=0,β0,β1,…,βp∈}
(4)
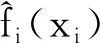

(5)
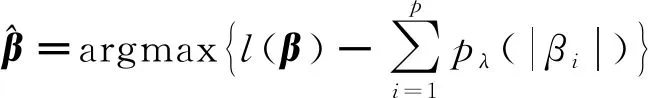
(6)
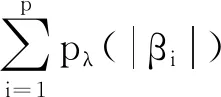

(二)提出基于二元核密度估计的二分类方法
FANS方法在进行特征变换时只采用了单个变量的核密度估计进行特征变换,并没有考虑到变量间可能存在的相关性,但现实生活中变量间常存在一定的相关关系。因此,本文在FANS思想的基础上,引入二元核密度估计进行特征变换。二元核密度估计刻画的是两个变量之间的联合分布。设有二元随机向量Z=(X,Y),其中X,Y均是一元随机变量,Z的概率密度函数为f(z)=f(x,y)。假设有n个观测样本z1,z2,…,zi,…,zn,其中zi=(x,y)。根据核密度估计是一个加权和的思想可得Z的二元核密度估计为:
(7)
其中,h1,h2是Z的两个分量上的带宽。k(·)是二元核函数,一般是通过乘积核函数来构造,即二元核函数等于一元核函数的乘积,k(u)=k1(u)·k2(u),这里,k1(u),k2(u)是两个一元核函数。核密度的估计需要选择合适的核函数和带宽,本文选择常用的Gaussian核函数,并通过拇指法则来确定带宽。由于计算带宽时需要用到四分位距,当四分位距为0时,带宽为0,无法进行核密度估计,所以只有当变量取值的四分位距不为0时,才能进行核密度估计[16]。以下假设{x1,x2,…,xp}在每个类别下取值的四分位距都不为0,实际应用中若变量不满足该条件,则不考虑该变量与其他变量的二元核密度估计。
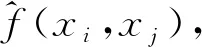
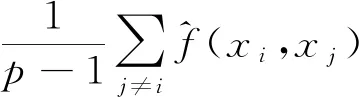
(8)
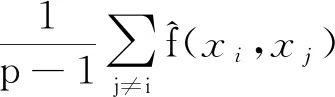
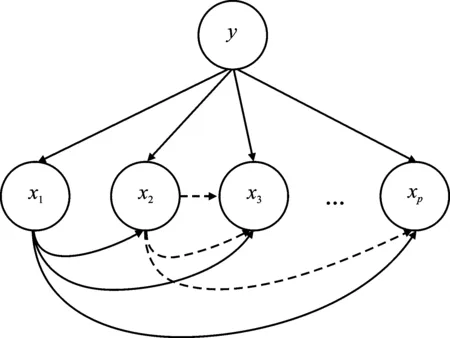
图1 AODE-FANS特征依赖关系示意图
其具体的决策边界为如下的模型:
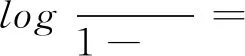

(9)
相应地,将原始特征和变换后的特征,同时用于构建决策边界的方法可称为AODE-FANS2。该分类模型如式(10)所示:

β2p+1x2+…+β3p-1xp
(10)
综上所述,AODE-FANS方法是对FANS方法的一种扩充,它在FANS方法的基础上引入了基于二元核密度估计的新特征。由于并没有改变FANS方法的模型设定,所以AODE-FANS方法和FANS方法在理论上的稳健性是一致的。
(三)多分类FANS方法和多分类AODE-FANS方法
前文的FANS、FANS2、AODE-FANS和AODE-FANS2等方法都只能处理二分类问题,如若解决多分类问题,还需将这些方法扩展。从文献综述可知,从二分类到多分类方法的扩展可以通过将多分类问题分解成多个二分类问题来实现。这其中比较有效的方法是One-vs-One方法。One-vs-One的基本思路是,假设有N个类别C1,C2,…,CN,将C1,C2,…,CN两两组合,每两个类别的数据放在一起作为一个子问题构建二分类器,每个测试样本需要分别用每个二分类器进行分类,然后采用多数投票法得到最终的分类预测结果。图2所示即One-vs-One方法的原理示意。

图2 二分类到多分类One-vs-One方法原理示意图
如图2所示,假定有4个类别时,根据One-vs-One的思路,需要构建6个分类器f1,f2,…,f6,将一个未知类别的测试样本分别代入f1,f2,…,f6,有3个分类器将其预测为C3,2个分类器将其预测为C1,1个分类器将其预测为C2。根据多数投票法,该样本的最终分类预测结果为C3。
本文采用One-vs-One的方法,将多分类问题分解成多个二分类问题,在每个二分类问题上分别使用FANS、FANS2、AODE-FANS及AODE-FANS2等方法,然后通过大多数投票集成这些二分类问题的分类结果,以此来解决多分类问题。在此,本文将这种One-vs-One方法下的FANS及AODE-FANS等方法分别称为OFANS、OFANS2、OAODE-FANS及OAODE-FANS2。
三、模拟验证
为验证上述所提的AODE-FANS及多分类的OFANS、OAODE-FANS等方法在解决复杂数据类别重叠、非线性可分问题中的有效性,本文进行了模型验证。需要说明的是,这里设计了两种形式的模拟,主要是模拟二分类及多分类中类别重叠、非线性可分的情形。在这两种模拟中,数据维度设置为100(p=100),每个类别的样本量设置为300(n=300)。随机抽取数据集中3/4的数据作训练集,其余1/4的数据作测试集,整个模拟过程重复100次,计算平均分类正确率来比较不同方法的分类效果。用于比较的方法分别是FANS、FANS2、AODE-FANS、AODE-FANS2以及带Lasso惩罚项的Logistic回归模型(PLR)。
另外,在进行特征变换的过程中需要将训练集数据(D)随机划分成两等份(D1,D2),用D1中的数据估计核密度函数,用D2中的数据代入核密度函数中得到核密度函数值,用于特征变换。为了保证方法的稳定性,需要将该划分过程重复多次,其中的划分次数记为L。考虑到数据划分次数对分类结果可能有影响,本文设定了三组不同的数据划分次数(L=3,L=5,L=7)。为反映变量间相关性对各种方法分类效果的影响,本文还设置了3组不同的相关系数(ρ=0,ρ=0.5,ρ=0.9)。需要说明的是,在计算二元核密度估计的过程中,如果变量xi在某个类别下取值的四分位距为0,则不考虑它与其他变量对应的二元核密度估计。
(一)模拟验证一
该模拟验证主要是模拟二分类中非线性可分的情形,以比较和说明本文所提二分类方法的分类效果。这里采用的是多元正态分布,两个不同类别分别来自不同的多元正态分布,即:
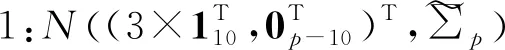
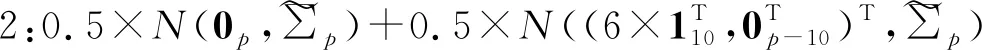
其中,类别1和类别2具有相同的均值向量和协方差,以近似模拟类别重叠非线性可分的情形。需要说明的是,类别2中,通过权重取值0.5和0.5组合两个多元正态分布(取值并不唯一,其他的权重组合也能达到类似的效果,但等权混合能保证在不同的相关系数下,两个类别始终是非线性可分的)。将模拟生成的数据进行主成分分析降维,根据前两个主成分得分做散点图,如图3所示,从左往右依次是ρ=0,ρ=0.5,ρ=0.9时模拟数据的降维散点图。
从图3可以看出,本文所模拟的两类数据确实存在类别重叠、非线性可分的情况。在此情形下,几种方法的分类准确率如表1所示。
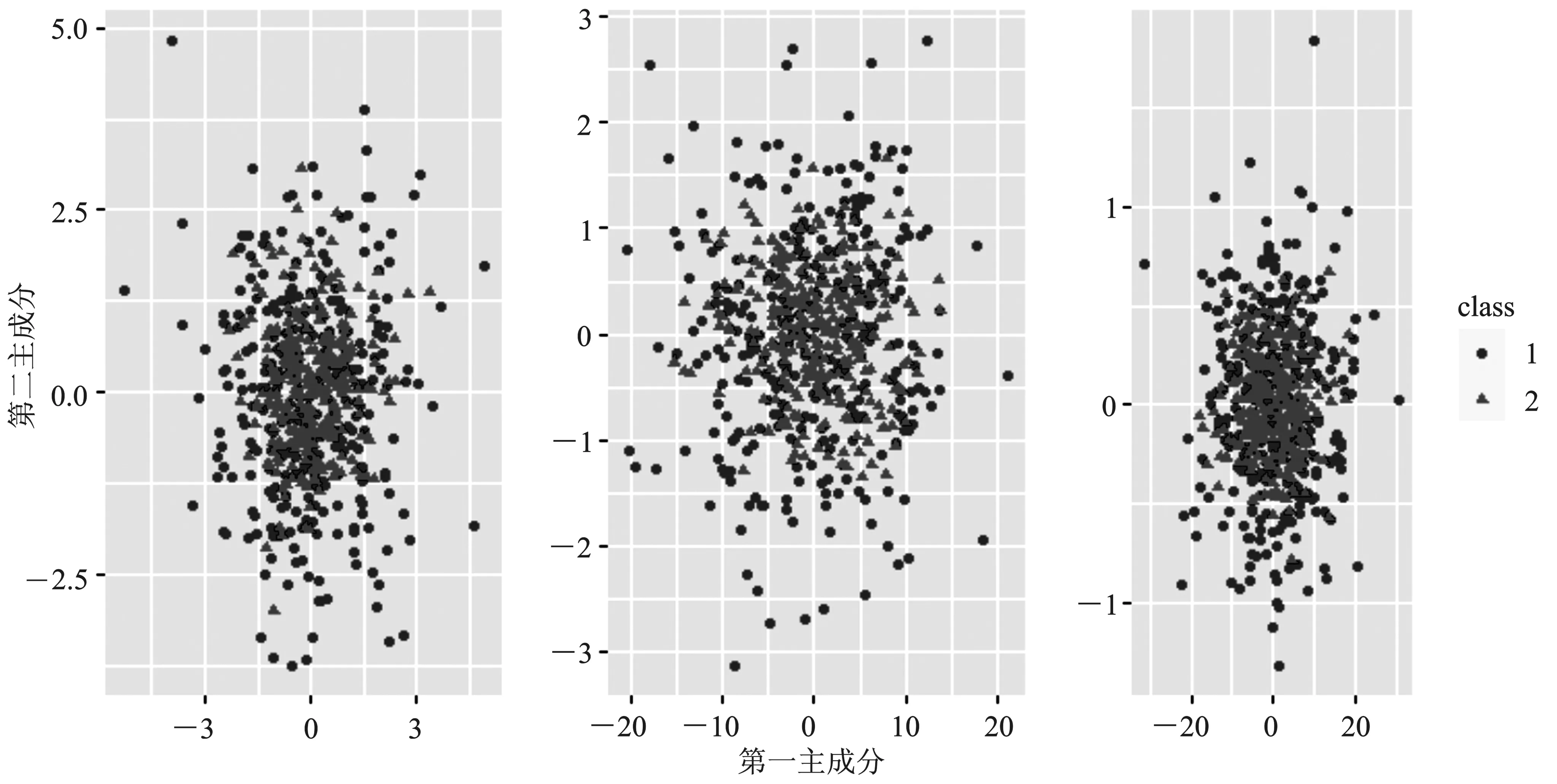
图3 模拟一生成的两类数据的降维散点图
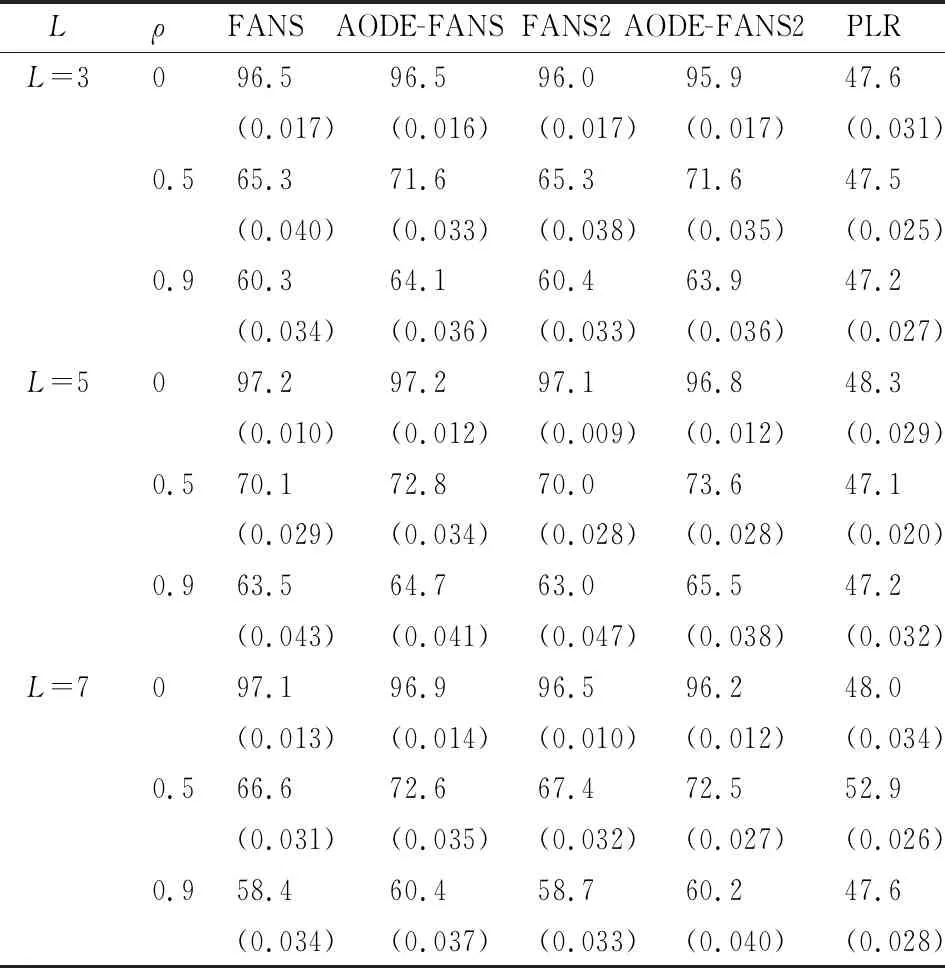
表1 二分类情形下几种分类方法的分类正确率(%)
从表1可以看出,由于两个类别相似度较高,带Lasso惩罚项的Logistic回归模型分类效果较差。当自变量之间的相关系数ρ=0时,引入二元核密度估计的AODE-FANS和AODE-FANS2方法的分类效果并没有优于FANS和FANS2方法。当自变量之间的相关系数ρ≠0时,引入二元核密度估计的AODE-FANS和AODE-FANS2方法相比于FANS和FANS2的方法,表现出了一定的优势。从分类正确率的标准差来看,原有方法与改进的方法均比较稳定。
(二)模拟验证二
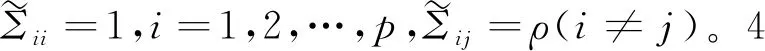
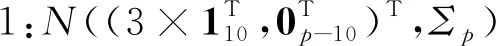
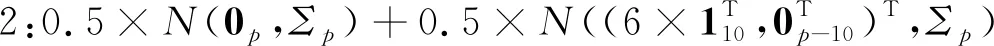
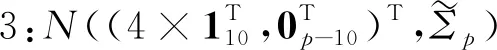
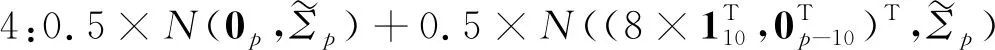
由于类别之间相似度较高,因此可以模拟类别间非线性可分的情形。两个正态分布组合的权重取值0.5和0.5(权重取值并不唯一,其他的权重组合也能达到类似的效果,但等权混合能保证在不同的相关系数下,四个类别始终是非线性可分的)。将模拟生成的数据进行主成分分析降维,根据前两个主成分得分做散点图,如图4所示,从左往右依次是ρ=0,ρ=0.5,ρ=0.9时模拟数据的降维散点图。
从图4可以看出,类别1、类别2、类别3和类别4都存在类别重叠、非线性可分的现象。在此情形下的各种分类方法的分类正确率如表2所示。

图4 模拟二生成的四类数据两个主成分得分散点图
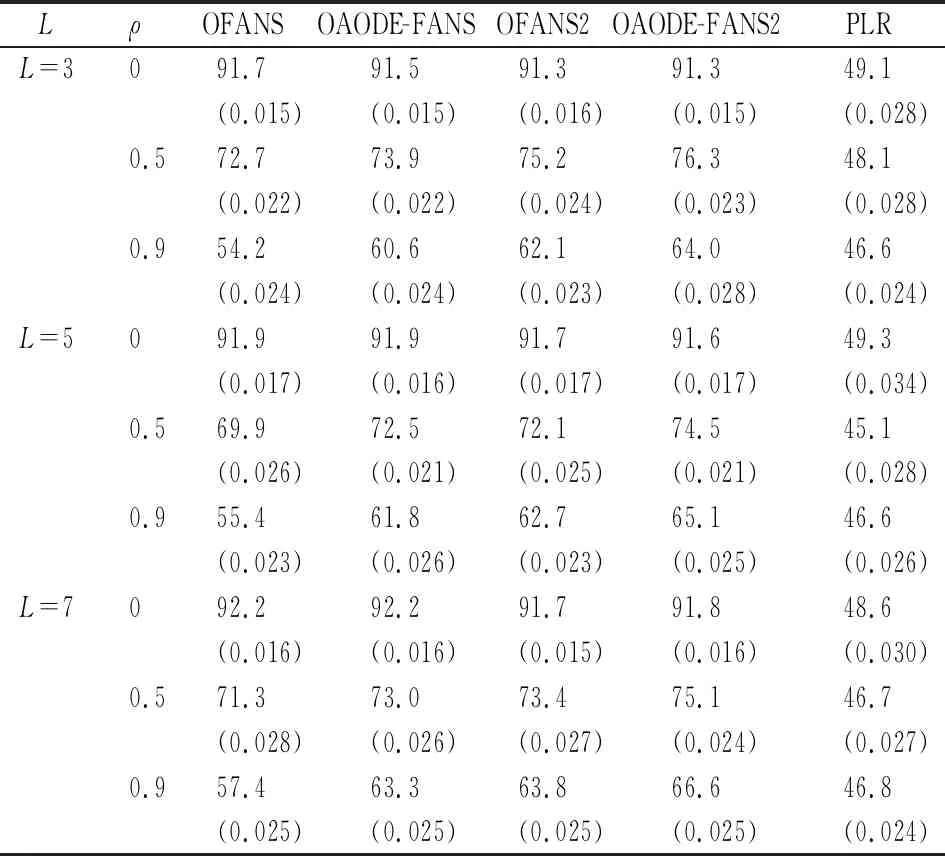
表2 多分类情形下几种方法的分类正确率(%)
从表2可以看出,在多分类非线性可分的情形下,采用非参特征变换的FANS和AODE-FANS等方法的分类效果要明显优于Logistic回归模型;且当变量之间存在相关关系时,OAODE-FANS、OAODE-FANS2方法的分类效果优于OFANS、OFANS2方法。同样,从分类正确率的标准差来看,原有方法与改进方法都比较稳定。此外,当自变量之间的相关系数ρ≠0时,OAODE-FANS2方法的分类效果要优于OAODE-FANS方法。
四、实例验证
为进一步说明AODE-FANS、OAODE-FANS在复杂数据非线性可分问题上的有效性,这里选择了两个实例进行比较和验证。这两个实例分别是文本分类中的垃圾邮件识别和图片分类问题。它们在一定程度上体现了复杂数据非线性可分、数据形式多样化的特点。
(一)垃圾邮件的识别
垃圾邮件的识别是目前较常见的二分类的文本分类问题。本文采用的是垃圾邮件分类(Spam)数据集,它是Hewlett-Packard实验室收集的关于电子邮件的数据(1)该数据来源于http:∥archive.ics.uci.edu/ml/datasets/Spambase。。该数据集中变量普遍存在一种非常弱的相关关系,因此对该数据集的验证可以反映出变量间相关关系强弱对FANS及ADOE-FANS方法分类效果的影响。
1.数据说明。Spam数据常被学者用于验证各种二分类分类方法的分类效果。Fan和Hastie等都曾将Spam数据用于实例验证[5,17]。该数据集包含 4 601 封电子邮件,其中含 2 788 封非垃圾邮件和 1 813 封垃圾邮件。每封邮件由58个变量来描述,其中包括57个条件变量,主要是词汇、数字和标点符号出现的频率等;1个类别变量,表明每封邮件是否为垃圾邮件。表3展示了部分变量的内容。
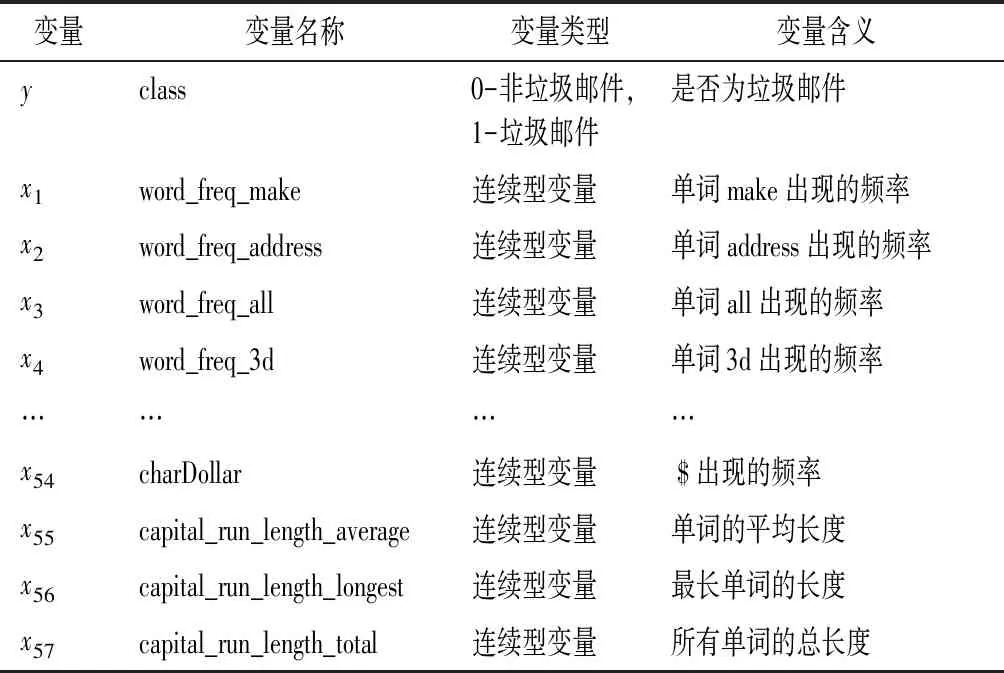
表3 Spam数据集变量列表(部分)
图5是根据Spam数据集中57个变量两两变量的相关系数所做直方图。从直方图可以看出,该数据集中绝大部分变量间相关系数绝对值小于0.2。
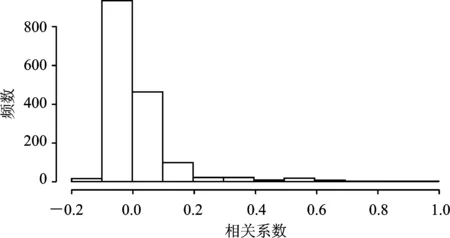
图5 Spam数据集变量相关系数直方图
2.分类结果。本文首先将Spam数据集按3∶1的比例划分训练集和测试集,将模拟验证中提到的五种方法用于训练模型,并用于对测试集数据进行分类,以评估模型的分类效果。为消除偶然因素,本文将此过程重复100次。图6是各种方法在Spam数据集上分类正确率箱线图。
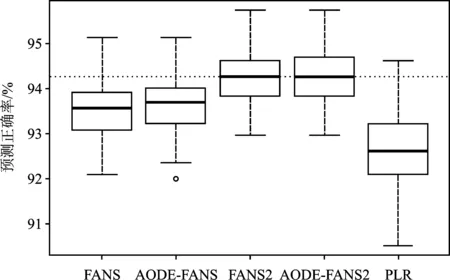
图6 各种方法在Spam数据集上分类正确率箱线图
从图6所示的箱线图可以发现,在Spam数据上,改进后的AODE-FANS方法分类效果比FANS方法略好,AODE-FANS2的分类效果与FANS2效果相当,但是它们都优于带Lasso惩罚的Logistic回归模型。表4是重复100次的平均分类正确率列表。

表4 Spam数据平均分类正确率及标准差
从表4中可以看出,在Spam数据集上由于变量间的相关关系较弱,甚至没有相关关系。因此,加入二元核密度估计特征变换的AODE-FANS方法的分类效果并没有明显提升,与FANS方法分类效果相当。
(二)图片分类
图片分类也是目前较流行分类问题。本文用Carla Brodley教授提供的图片分类数据集——Image Segmentation数据集(2)该数据集来自https:∥archive.ics.uci.edu/ml/datasets/Image+Segmentation。。该数据集与Spam数据集不同,它是多分类,且其变量间的相关关系较明显,因此选择该数据集可以验证和比较多分类情形下变量间有明显相关关系时,OFANS及OAODE-FANS方法的分类效果。
1.数据说明。Image Segmentation数据集是取自于7种不同类型的户外图片,每种类型均有330张图片。将这些图片划分成3×3的区域,对每个区域统计它的颜色、像素情况。因此,该数据集共有20个变量,其中19个变量用以描述图片的颜色、像素、饱和度等,1个变量是类别变量,以说明图片所属类别。具体的变量名称及含义如表5所示。

表5 Image Segmentation数据集变量说明
同样,将表5中19个变量间相关系数做直方图,如图7所示。可以看出,与Spam数据集变量间相关关系较弱的情况不同,Image Segmentation数据集中,部分变量间的相关关系是比较明显的。
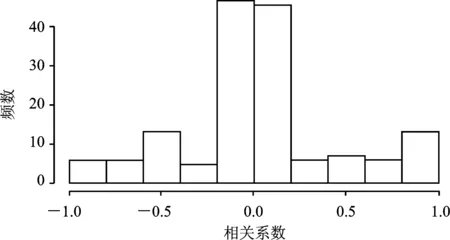
图7 Image Segmentation数据集变量相关系数直方图
2.分类结果。将Image Segmentation数据按 3∶1 的比例划分成训练集和测试集,利用训练集数据分别训练OFANS、OAODE-FANS、OFANS2、OAODE-FANS2及Lasso惩罚的Logistic回归模型,并据此对测试集中的图片进行分类。将此过程重复100次得到图8所示的结果。
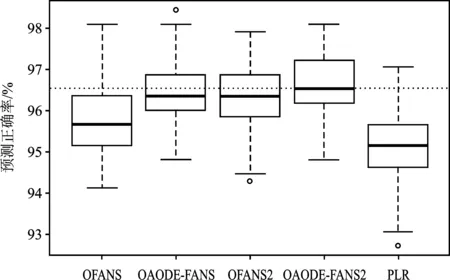
图8 不同方法分类正确率箱线图
从图8可以看出,OFANS、OAODE-FANS、OFANS2及OAODE-FANS2的分类效果不仅均优于Lasso惩罚的Logistic回归模型,并且在变量存在明显相关关系的情况下,OAODE-FANS方法的分类正确率要高于OFANS方法,OAODE-FANS2方法的表现也要优于OFANS2方法。这说明在变量存在相关关系的情况下,引入二元核密度估计的特征变换能够更好地处理类别间重叠、非线性可分的问题。
表6所示是重复100次的平均分类正确率列表。从表6中可以看出,在Image Segmentation数据集上,多分类FANS、AODE-FANS等方法的平均分类正确率是要大于Lasso惩罚的Logistic回归模型的,且引入二元核密度的多分类AODE-FANS、AODE-FANS2方法平均分类正确率大于多分类FANS、FANS2方法,这说明在处理多分类问题中当变量间相关性比较明显时,采用特征变换并引入二元核密度估计能在一定程度上提升分类正确率。

表6 Image Segmentation数据平均分类正确率及标准差
五、结 论
本文在Fan等提出的FANS方法基础上,提出结合半朴素贝叶斯分类思想中的AODE方法,引入二元核密度估计(刻画变量间的相关性)进行特征变换构建决策边界的方法,即AODE-FANS方法,用以解决二分类问题中变量存在相关关系且类间重叠、非线性可分的问题。并且,通过One-vs-One的方法将已有的FANS和本文所提的AODE-FANS方法扩展至多分类问题,从而得到OFANS和OAODE-FANS方法。通过模拟数据和实例验证表明它们在二分类和多分类问题上均具有较好的分类效果,且在存在明显变量相关性时,AODE-FANS的分类效果要好于FANS方法。

