基于云模型和前景理论的语言评价双边匹配决策研究
毕傲睿,骆正山,孙志远,张新生
(1.淮阴工学院 管理工程学院,江苏 淮安 223003;2.西安建筑科技大学 管理学院,陕西 西安 710055)
一、引 言
生活和工作中存在各种匹配现象,如婚姻匹配、读者与杂志广告匹配、大学招生配额匹配、供需匹配、风险投资商与风险企业匹配等[1-4]。这些匹配问题多数为双边匹配(Two-sided matching,TSM),即互有需求的主体双方相互评判和选择的过程。合理的匹配可以增加主体双方的满意度和认可度,从而提高社会工作和生活的和谐性,因此,无论从管理学、社会学还是经济学角度,双边匹配问题的研究都具有积极的意义。
自2012年Roth和Shapley在匹配研究的基础上实现稳定分配及市场设计实践理论而获得诺贝尔经济学奖以来,双边匹配问题在中国开始受到大量关注,一些学者从多角度进行了研究,如:乐琦对序值信息应用Borda分值进行转化,在此基础上构建匹配矩阵并进行匹配决策[5];樊治平等针对完全序值信息前提下双方主体还具有最低可接受偏好序要求的匹配问题提出一种严格双边匹配决策方法[6];孔德财等设计了偏好序列表的简化规则,在此基础上以主体序值和最小为目标函数,解决了一对多双边匹配问题[7];姜艳萍等为解决序区间形式偏好信息匹配问题,计算了序区间之间的优劣可能度并给出了基于可能度的弱稳定匹配、强稳定匹配等四种匹配解决方案,初步体现了考虑模糊评价信息的匹配问题的思想[8]。
虽然已有研究解决了多种形式的双边匹配问题,但几乎所有匹配问题的偏好信息都必须包含一个序值前提(如完全偏好序、强偏好序等),而这种序值本质上是为解决双边匹配问题提供的一个特殊假设条件,也是决定最终决策结果的主要条件。但通过调查分析发现给出序值前提在理论上可行而在现实中的可行性却较低。现实中匹配主体给出的偏好多是基于语言评价给出的概念,例如择偶:男A对女B的评价通常是满意、一般或者不满意,很少会给出具体值(如满分100分给出80分),因为现实中很少有人会专门去制定具体的评分标准并且也没有为大众所共同认可的评分。已有心理学实验证明普通人对事物进行判别时能正确区别的极限在5~9之间,因此存在较多评价对象时一般很难给出一个可信度高的序值[9]。匹配决策的意义在于后期通过有效方法处理匹配主体提供的偏好内容而不是在前期让主体对提供的偏好信息进行预处理,这增加了主体双方的工作难度。因此考虑序值的双边匹配决策在语言评价偏好问题中适用性较弱,而目前专门针对语言评价偏好进行匹配决策的研究还很少,主要难点是缺乏将定性语意转为定量标值的处理方法,现有一些研究基本都是以得分信息界定语言变量,这种硬性划分忽略了语言评价信息的模糊性和不确定性[10]。除上述外还需注意的是现有双边匹配研究中的主体通常是抽象化的,一般默认是完全理性的个体,即匹配过程中主体心理行为因素的作用被忽略了,而现实大部分匹配问题中的主体往往是人,是有限理性的,即匹配双方对彼此的判断通常基于自我认知和经验的风险考量,或者在有旁者参与的情况下产生一些积极或消极的影响。
为此,本文针对主体偏好信息为语言评价的双边匹配问题,应用云模型(Cloud Model)表示主体给出的自然语言评价信息,更加客观地解决了偏好信息的定量化处理问题,以体现双方主体的认知度的模糊性和不确定性;以灰关联度计算前景效用价值,体现主体心理态度,综合提出一种基于云模型和前景理论的语言评价双边匹配决策方法。
二、语言评价双边匹配问题描述
(一)双边匹配概念
设存在甲、乙两方主体,令甲方主体集合为A={A1,A2,…,Am},m≥2,其中Ai表示甲方第i个主体,i=1,2,…,m。乙方主体集合为B={B1,B2,…,Bn},n≥2,其中Bj表示第j个乙方主体,j=1,2,…,n。假设m≤n。
定义1[11]:对于一一映射关系μ:A∪B→A∪B,且∀Ai∈A,∀Bi∈B满足以下条件:
(1)μ(Ai)∈B∪Ai,若μ(Ai)=Ai,则称Ai没有匹配对象;
(2)μ(Bj)∈A∪Bj,若μ(Bj)=Bj,则称Bj没有匹配对象;
(3)μ(Ai)=Bj,当且仅当μ(Bj)=Ai,则μ满足双边匹配,其中μ(Ai)=Bj表示Ai与Bj在μ中的匹配;μ(Bj)=Bj表示Bj与自身匹配,在μ中为自由,也就是未匹配。
定义2[12]:设Ai,Ae∈A,Bj,Bl∈B,i≠e,j≠l;θij(A)、θij(B)分别表示Ai对Bj、Bj对Ai的满意度。若μ中未曾出现以下情况:
(1)μ(Ai)=Bl,μ(Ae)=Bj,满足θij(A)>θil(A)且θij(B)>θej(B);
(2)μ(Ai)=Bl,μ(Bj)=Bj,满足θij(A)>
θil(A);
则此时μ为稳定匹配。
(二)语言评价
语言评价是用语言变量来描述现实中各种现象的近似表征,不同于精确表征(例如以图片描绘事物)语言变量的取值为自然语言的词语。一般具有层次划分的语言形式评价词汇集例如{好、一般、差}、{很满意、满意、基本满意、不满意、很不满意}等,其中语言变量的个数称作该评价集的粒度。具体语言评价集定义如下:
定义3[13]:一个由奇数个语言变量构成的语言集合ST={s0,s1,…,si},其中i=0,1,…,T;T+1为ST的粒度,且si随着i的增加其代表的含义也越来越好。ST满足以下条件:
(1)有序性:当i≥j时,si≥sj;
(2)可逆性:存在逆运算算子Neg(si)=sj,j=T-i;
(3)极值运算:当si≥sj,即si不劣于sj时,有max{si,sj}=si,min{si,sj}=sj。
(三)基于语言评价的双边匹配问题
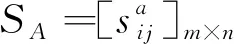
三、理论背景
(一)云模型
云模型(Cloud Model)是由中国工程院院士李德毅教授提出,是处理定性概念和定量数值描述的不确定转换模型[14]。它把模糊理论中的模糊性和概率论中的随机性完全融合在一起,实现了定性和定量的相互映射,自提出以来已成功应用到决策分析、数据挖掘、自然语言处理等领域,因此本文应用云模型表示主体偏好的语言评价。
1.云模型基本概念
设C是定量论域U上的定性概念,若论域U中任意元素x对C的隶属度u(x)∈[0,1]是一个具有稳定倾向的随机数,则C从论域U到[0,1]的映射在数域空间的分布称为云。云由大量云滴组成,每一个云滴即为定性概念在数量上的一次随机实现,云的整体形状反映了定性概念的整体特性。
2.云的数字特征
云用期望Ex、熵En和超熵He三个数字特征来整体定量表征一个定性概念,通常记为C(Ex,En,He),主要作用区域为[Ex-3En,Ex+3En]。云滴在论域空间分布的期望Ex是最能代表定性概念的典型点值,反映了云的中心位置。熵En是定性概念模糊性和随机性的综合度量,一方面反映了论域空间中可被定性概念接受的云滴的取值范围,另一方面又能反映云滴的离散程度。超熵He是熵的不确定性度量,表示样本出现的随机性,反映了云的凝聚程度。
由上述概念可知,对语言评价来说每个云滴就是语言变量在数量上的一次具体实现。因为每个云滴都是随机产生的,且代表定性概念的确定程度也是模糊的,虽然单个定量数值属于一个定性概念语言的不确定变化不会影响到云的整体特征,但是一定数量的云滴整体分布特性就体现了定性语言的模糊性和不确定性。例如对某个学生来说考试得95分可以接受是“满意”,但得90分也可以接受代表“满意”,只不过通过云映射考试得95分这个云滴代表“满意”的确定程度是1,得90分这个云滴代表“满意”的确定程度是0.9,加上所有如91、92分等云滴累计到一定数量,在论域中就形成一个云来表示语言变量“满意”这个概念。
(二)前景理论
前景理论由Kahneman和Tversky提出,该理论指出:现实中的人是有限理性的,在面临决策时其风险偏好会随得失心态变得不同[15]。也就是说前景理论认为现实人对待收益和损失的态度是不一致的:对于收益会表现得风险规避,对于损失却变得风险追求;而具体的收益和损失则需要一个参照点进行凸显,所以人们在不确定、模糊性或者犹豫性条件下对待风险的态度在概率上具有某种非线性的关系。这与直觉模糊双边匹配问题中主体风险偏好的态度是一样的,因此考虑前景理论得到的匹配更符合现实人的决策行为[16]。前景价值是由价值函数和决策权重共同决定的,即:
v=v(x)++v(x)-
=π(pi)+v(Δxi)+π(pi)-v(Δxi)
(1)
式(1)中,Δxi是决策值xi与参照点的差值,Δxi为正表示收益,反之表示损失;π(pi)+和π(pi)-是权重函数,是概率评价性的单调增函数,权重函数计算如下:
(2)
式(2)中,pi是决策值xi发生的概率;γ+、γ-是风险态度系数,用于控制权重函数曲线的曲率。
v(Δxi)是价值函数,是决策者主观感受形成的价值,Tversky和Kahneman给出的价值函数的形式为幂函数:
(3)
式(3)中,参数α、β分别为收益和损失区域价值幂函数的凹凸程度,α、β<1表示敏感性递减,系数θ表示损失区域比收益区域更陡的特征,θ>1表示损失厌恶。
四、匹配决策过程
(一)云模型转换
利用云模型实现语言变量的定性转换。因为正态云具有普适性,本文将语言评价集中的语言变量分别表示为正态云模型,即云模型数字特征满足:
(4)
以5粒度语言评价集为例,设语言评价集{很满意、满意、基本满意、不满意、很不满意},考虑到自然语言的和谐性采用黄金分割率将5个语言变量表示成5类云模型。令中间云为C0(Ex0,En0,He0),其左右相邻云分别为C-1(Ex-1,En-1,He-1)、C+1(Ex+1,En+1,He+1)、C-2(Ex-2,En-2,He-2)以及C+2(Ex+2,En+2,He+2),具体数字特征如下:
(5a)
(5b)
(5c)
令有效论域区间为[0,1],He0在5粒度下一般取值0.005,计算得“很满意”对应云模型(1,0.104,0.013),“满意”对应云模型(0.691,0.064,0.008)、“基本满意”对应云模型(0.5,0.039,0.005)、“不满意”对应云模型(0.309,0.064,0.008)、“很不满意”对应云模型(0,0.104,0.013)。评价语言的云模型模拟如图1所示,从图中可看出云模型就是在考虑模糊性和不确定性的前提下将语言变量在论域中表示,其中接近论域中心云的熵和超熵越小,即模糊性和不确定性越小,反之越大,因此云模型可以有效表示定性的语言变量。以各语言变量的云模型期望值作为匹配双方的满意度值分别构建偏好矩阵。
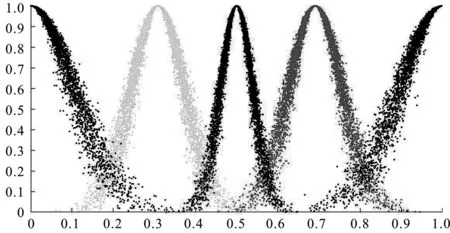
图1 评价语言的云模型图
(二)构建前景矩阵
以偏好矩阵的最优和最劣偏好构建正负理想方案,因为利用前景理论进行决策时,一般人们更在乎的是结果与理想方案的差距而不是结果本身,因此本文应用灰关联思想对前景理论中价值函数进行改进,在主体偏好与正负理想方案相应绝对差的基础上计算灰关联系数,正负灰关联系数计算如下:
(6a)
(6b)
式中,ξij为甲方第Ai主体对乙方Bj主体的偏好与理想方案的关联系数;X+、X-分别为正负理想方案,aij为偏好值;ρ为分辨系数,一般取值0.5;参数α=β=0.88;θ=2.25。同理计算乙方对甲方偏好与理想方案的关联系数。
将正负灰关联系数带入效用价值函数得:
(7)
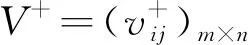
(三)决策模型

(8a)
(8b)
(8c)
tij∈{0,1}
(8d)
目标函数的含义是最大化A方主体对B方主体的前景值之和、最大化所有B方主体对A方主体的前景值之和;约束条件的含义是每个A方主体必须且只能与一个B方主体匹配,而每个B方主体最多只能与一个A方主体匹配。
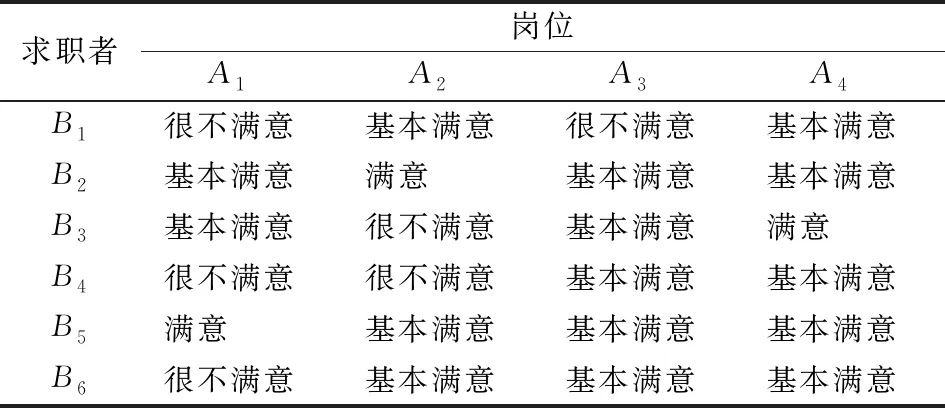
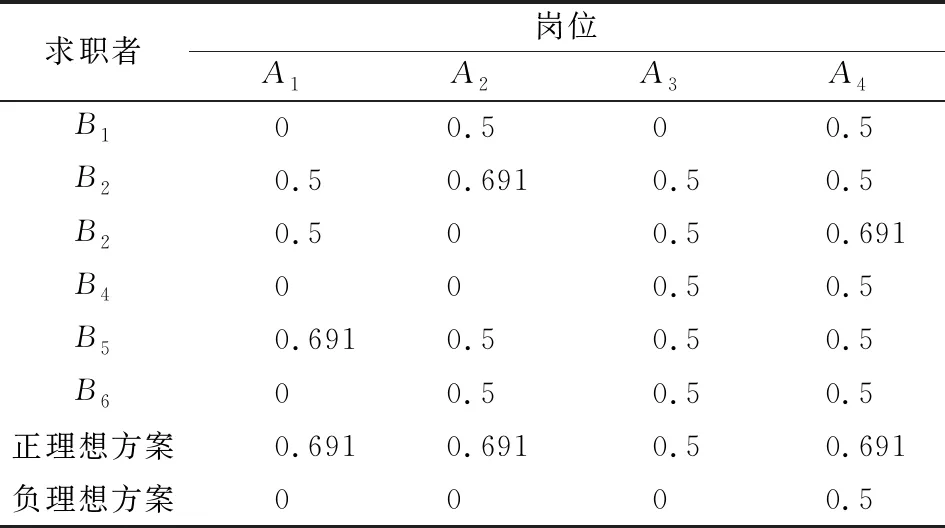
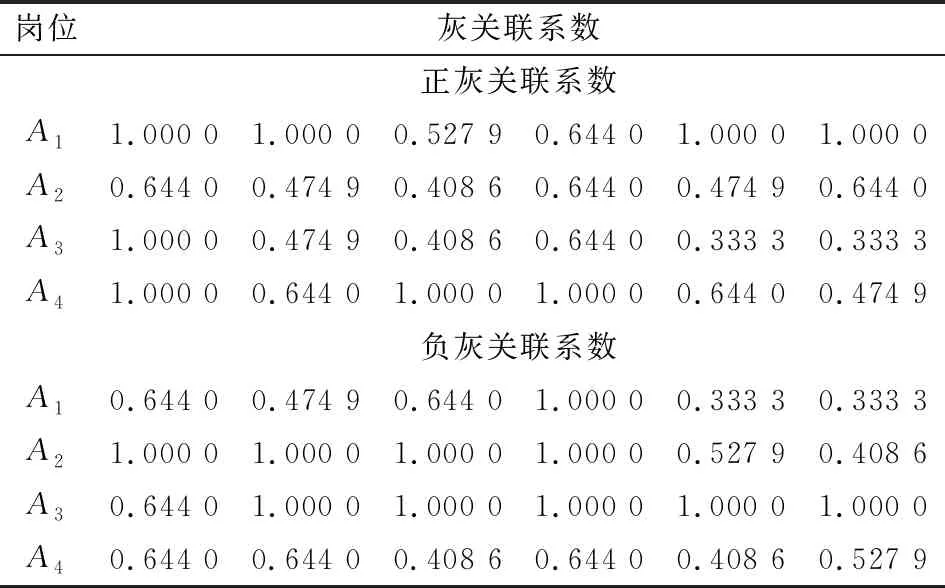
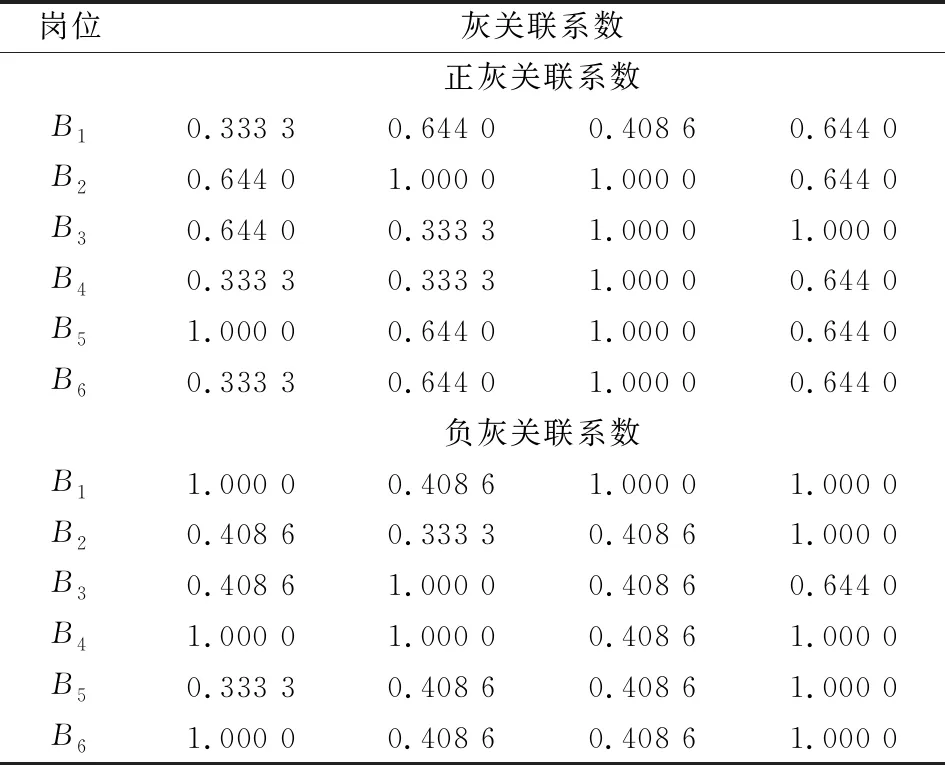
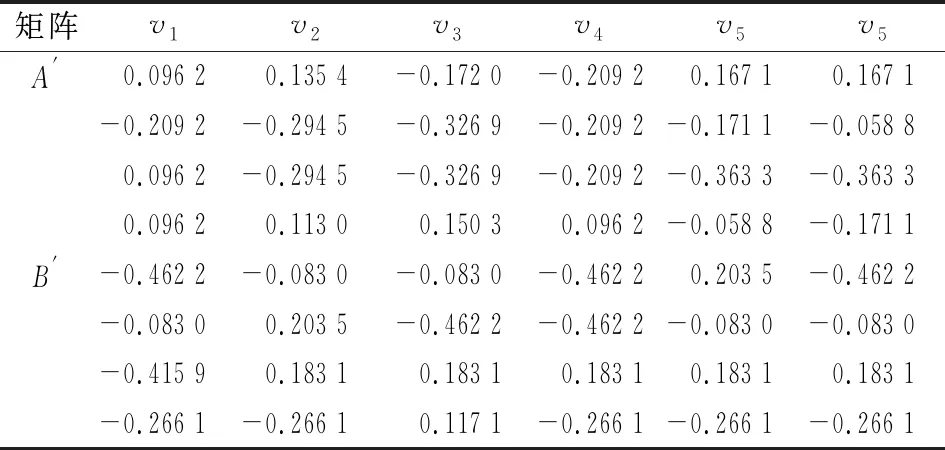
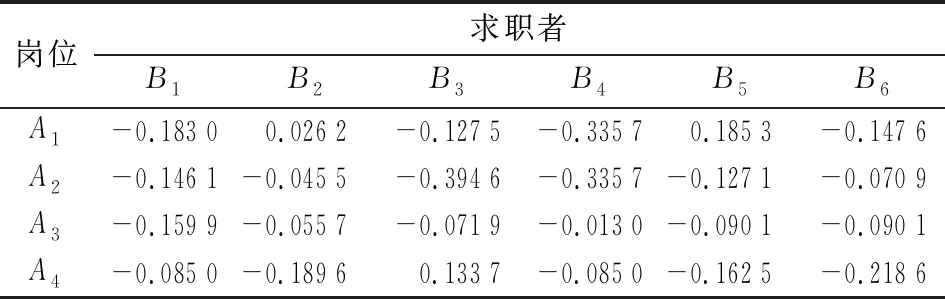
为求解目标优化模型,设wA和wB分别表示GA和GB的权重,满足0 (9) 根据式(5)将5粒度语言评价矩阵SA和SB分别用对应的云模型表示,以5个云模型的期望值作为匹配双方的偏好数值,同时以双方主体的整体偏好最优最劣分别确定正、负理想方案,见表3和表4。 表1 岗位领导的偏好语言评价矩阵 表2 求职者的偏好语言评价矩阵 表3 岗位领导的偏好期望矩阵 表4 求职者的偏好期望矩阵 由式(6)计算的各主体偏好到正负理想方案的灰关联系数见表5和表6。 表5 岗位领导的偏好到正负理想方案的灰关联系数 表6 求职者的偏好到正负理想解的马氏距离平方 依据关联系数建立主体A、B的正负前景矩阵,同时考虑到匹配双方主体之间是相互平等评价的,故概率值分别为1/6和1/4,依据式(2)求得的权重,建立规范化前景矩阵A′、B′。 表7 规范化前景值 由规范化前景矩阵A′、B′构建多目标优化模型,因为wA=wB,为方便求解进一步转换为单目标优化模型,其中系数矩阵C=[cij]4×6见表8。 表8 系数矩阵 应用Lingo11.0软件包求解得最大值为0.260 4,匹配结果为:μ={[A1,B5],[A2,B2],[A3,B4],[A4,B3],[B1,B1],[B6,B6]},即B5被A1岗位录取,B2被A2岗位录取,B4被A3岗位录取,B3被A4岗位录取,B1和B6没有获得实习资格,同时根据定义2,该匹配方案为稳定匹配的最优结果。 现实中的双边匹配问题多是基于主体偏好为语言评价信息的情况,而为了丰富语意内涵和增加表达效果语言评价信息通常具有模糊化的特点,主体人还具有风险规避和追求的心理特征,因此语言的模糊化和人的心态特征影响着匹配决策的结果。本研究通过云模型计算语言偏好信息的定量表达值,以灰关联系数建立规范化前景矩阵,进而通过求解目标优化模型获得匹配方案。该方法有如下特点:一是考虑了定性语言变量转为定量偏好值过程中的模糊性和不确定性信息,减少了硬性得分导致的信息损失;二是将主体面对收益和损失具有不同的风险态度等心理行为特征纳入考量,从实际应用角度进行了匹配决策。该方法合理而精确的为解决主体偏好为语言评价信息的双边匹配问题提供了一种新思路。 目前国内对匹配问题的研究还比较少,尤其针对语言评价信息的双边匹配问题研究更加缺乏。本研究虽然采用了云模型进行定性语言信息与定量数值间的转换,但是这种方式是基于自然规律的一种广义转换,前提是假设匹配双方所有主体的评价态度划分都是基于同样的基准(黄金分割)的,而现实中常有特殊偏好或者兴趣的主体,因此更为合理的做法是对各主体的评价态度分别划分,在此基础上进行定性语言的转换,而如何进行评价态度划分以及对不同主体划分粒度的对应结合是未来可进一步的研究方向。
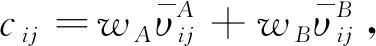
五、案例分析
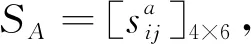


六、结论与展望

