一道质检试题多元表征下的求解思路探究*
2020-11-04 06:52福建省莆田第二中学351131蔡海涛
中学数学研究(江西) 2020年10期
福建省莆田第二中学 (351131) 蔡海涛
表征是外界事物的心理重现,是认知心理学中的一个非常重要的概念[1].数学问题的表征是解决问题的起点,同一个数学对象可以有多种表征形式.学生对数学问题的适当表征决定了对问题的理解和解答,学生解题困难往往是因为对数学知识不会“灵活应用”,而这种“灵活应用”就是需要我们学会选取适当的数学表征,进而解决问题.多元表征理论突出了学生的主体性,这需要教师用学生的角度去理解问题,以适应学生思维认知特点展开教学.教师尝试利用文字、符号、图形、操作等表现形式让学生体会到数学问题表征形式的多样性,创设更加多元丰富的教学情境,从不同角度激发学生的思维,促进学生自主探索和感悟.下面笔者以一道高三质检题为例,谈谈“多元表征”下实施解题教学的策略和体会.

本小题主要考察函数的零点、导数在研究函数性质中的应用等基础知识;考查推理论证、运算求解能力;考查转化与化归、函数与方程、数形结合思想.
1.获取题目表征信息,条件等价转化

(ⅰ)当0 通过对上述试题的求解思路分析,可以看出,一个具体的数学问题对象,往往具有多元表征.不同的数学表征在信息的表示上是等价的,但在思想方法的应用上各有不同,比如符号表征适合逻辑推理,图形的表征适合于直观想象.在数学的解题教学中,教师应该重视数学问题之多元表征,并在多元表征之间建立了联系,这样有助于数学解题变得更加有趣,同时充分利用这些表征也促进了学生对数学问题更深的理解.
2.变通条件表征方式,缩小参数范围



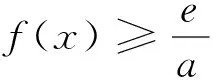


3.发掘图形表征信息,数形巧妙结合

猜你喜欢
理科爱好者(教育教学版)(2022年1期)2022-04-14
中学生数理化(高中版.高考数学)(2021年3期)2021-06-09
中学生数理化·高三版(2021年3期)2021-05-14
智富时代(2019年7期)2019-08-16
智富时代(2019年7期)2019-08-16
中学教学参考·理科版(2017年8期)2018-02-24
中学化学(2017年6期)2017-10-16
广西教育·B版(2017年1期)2017-05-03
中学化学(2017年2期)2017-04-01
小学生导刊(低年级)(2016年8期)2016-09-24

