2019年清华大学自主招生第11题的多解及推广*
华南师范大学数学科学学院 (510631) 蒋红珠 内江师范学院数学与信息科学学院 (641100) 刘成龙 张 玉
1.问题及简评

简评:本题内涵丰富、数学味浓、解法多样、可一般化.研究该题有助于学生加深知识理解、发展数学思维、完善认知结构、体验数学研究历程.因此,该试题是一个值得研究的好问题.
2.问题解决
问题解决常常被看作是能动的、不断发展的过程,是数学思维不断数学化的过程,是一个探索、发现、创新的过程.[1]从不同角度解决问题,有助于学生多角度理解问题,培养思维的深刻性和灵活性.
2.1最大值求解





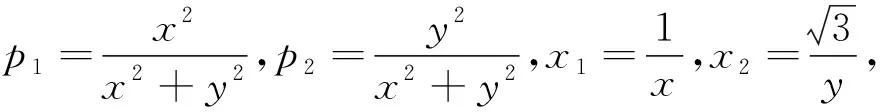
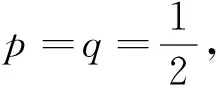
分析2:由“x2+(y-2)2≤1”的结构特征,想到三角代换.




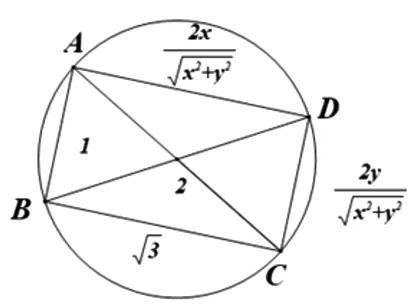
图1


图2

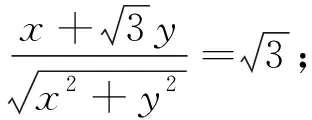

图3
评注:从分析1、2、3、4中可以看出,本题对学生逻辑推理、数学运算、数学抽象、直观想象和数学建模素养的考查十分深刻.在推理和运算中,促进了学生数学思维发展,形成规范化思考问题的品质,养成一丝不苟、严谨求实的科学精神.在数学抽象、直观想象和数学建模等核心素养的考查中,引导学生不断提高运用几何图形解决问题的意识、提升数形结合的能力、感悟问题的本质,培养创新思维.
2.2 最小值求解
3.问题拓展——基于推广的视角
问题推广是指在一定范围内或一定层次上对问题进行拓展,使之在更大范围或更高层次上成立,此外,也指对条件、结论进行结构分析以后,进行适当变化,使得到的新命题为真.[2]问题推广首先应认清问题的成立条件或适用范围;其次,需要把握条件或结论中呈现的结构;最后,需要弄清解决问题的方法我们可以从元个数、次数、系数和代数结构进行推广.
3.1 最大值的推广
由前文方法可知取最大值时,与条件“x2+(y-2)2≤1”没有关系,推广时可省略.

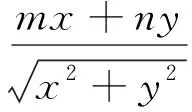


评注:推广1让学生认识到“特殊性”到“一般性”的思维方式;推广2揭示了多元变量关系的实质.这对学生回归理性、认识数学本质有引导作用.
3.2 最大值与最小值同时推广
分析1:从最大值的解法10中受到启发,圆盘是关于y轴对称的,但ON与圆盘相切,一般情形下结果又怎样呢?


分析2:如果圆盘不关于y轴对称,结果又是怎样的呢?(具体推广,请读者自行探究.)

