学好定义“百题通”
2020-11-04 04:48吴建明张启兆
中学生数理化·高一版 2020年10期
吴建明 张启兆
在高中数学的学习过程中,常会出现“老师一讲就会,自己一做就错”的现象。同学们知道原因出在哪里吗? 这主要是忽视了对定义的深刻理解,没有把握有关定义的本质。在解题时,如果能回归定义,许多问题便迎刃而解,可谓学好定义“百题通”。
一、把指数问题转化成对数问题
已知条件中含有指数式,而所求问题中没有指数式,可利用对数定义把指数式转化成对数式,再进一步化简求值。
解:已知条件是关于x,y 的指数式,而要求的结论中不含指数式。利用对数的定义,就可以将指数式转化成对数式,这样就能将x,y 从已知条件中“解”出来,再计算就容易了。
二、把对数问题转化成指数问题
已知条件中含有对数式,而所求问题中没有对数式,可利用对数定义把对数式转化成指数式,然后再进一步化简求值。
例3 已知logm2=x,logm3=y,求m3x-y的值。
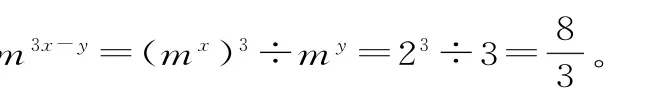
说明:解答本题的关键在于掌握指数式与对数式的互化。将未知问题(指数求值)转化为已知问题(对数求值)进行处理,这也是转化思想的具体应用。
说明:解答本题时,不注意“对数的真数必须大于零”这一隐含条件,就容易产生错解。
猜你喜欢
小学生学习指导(高年级)(2022年10期)2022-11-04
数学物理学报(2022年2期)2022-04-26
新世纪智能(数学备考)(2021年9期)2021-11-24
读写月报(初中版)(2021年12期)2021-05-25
新世纪智能(数学备考)(2020年9期)2021-01-04
中学生数理化·七年级数学人教版(2017年3期)2018-01-20
中学生数理化·七年级数学人教版(2017年12期)2017-02-15
中学生数理化·七年级数学人教版(2017年12期)2017-02-15
黄河之声(2016年24期)2016-02-03

