基于车-路耦合振动状态下沥青路面力学响应

严战友， 赵晓林， 陈恩利， 赵 勇， 赵国叶

(1. 石家庄铁道大学 土木工程学院， 河北 石家庄 050043; 2. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全重点实验室， 河北 石家庄 050043; 3. 北京交通大学 语言与传播学院， 北京 100089; 4. 爱尔康(中国)眼科产品有限公司， 北京 100020)

重载车辆是公路主要运输工具，其荷载不断增加，严重影响公路使用寿命.JTG D50—2017《公路沥青路面设计规范》规定，单轴双轮组100 kN为标准轴载，并将车辆荷载简化为均布双圆荷载.实际路面承受车辆随机动载，作用效果比静荷载复杂.针对路面响应问题，许多学者已得出一些有益结论.刘仕贵等[1]考虑4种常见荷载作用形式，即常载、超载、常载+刹车、超载+刹车，表明刹车引起水平荷载对弯拉应力、剪应力影响较大，超载对路表弯沉、弯拉应力影响显著.刘大维等[2]利用SIMPACK获得车辆动态荷载，导入沥青路面有限元模型，分析随机动载与移动恒载作用下柔性沥青路面动态响应特性.WANG H.等[3]测量轮胎-路面三向接触应力，实现三向接触荷载作用下沥青路面动力响应数值分析.综上，大部分学者在研究车-路相互作用时，未考虑橡胶轮胎的影响以及轮胎与路面非线性接触，因此研究结果与实际存在一定误差.

为此，利用ABAQUS，建立三维两自由度1/4车辆模型与黏弹性沥青路面模型，考虑橡胶轮胎以及轮胎与路面非线性接触，无需第3方多体动力学软件和子程序，研究车辆动载作用下，轮胎、路面响应及轮胎与路面接触行为.

1 模型构建

1.1 1/4车辆有限元模型及轮胎模型

建立三维两自由度1/4车辆有限元模型，见图1.

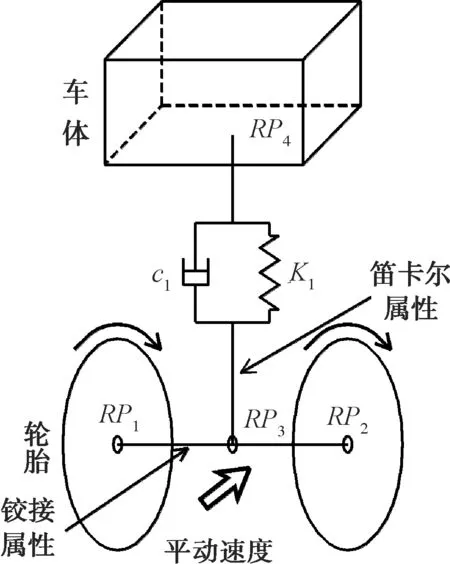
图1 1/4车辆模型简图

其中点RP1，RP2，RP3和RP4皆为中心参考点.车体为均质刚体，悬挂系统为线性弹簧和线性阻尼器并联，轮胎采用橡胶材料.车体质量为5.0 t；轮胎质量为0.7 t；悬架刚度K1=1 000 N·mm-1；悬架阻尼c1=15 N·s·mm-1.

采用11.00R20载重轮胎，利用Auto CAD绘制轮胎断面图，并导入ABAQUS生成三维实体轮胎，如图2所示.

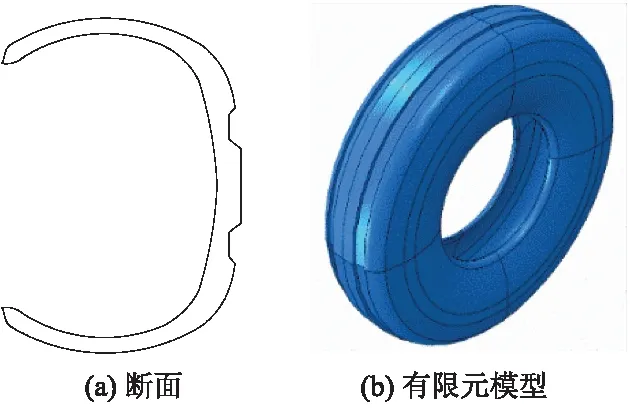
图2 轮胎模型

将橡胶轮胎模型适当合并与简化.Yeoh模型与橡胶试验数据拟合效果较好[4].采用该模型描述橡胶超弹性，其简化多项式函数如下：

(1)

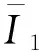
橡胶参数如下：C10=0.850 5，C20=-0.207 2，C30=0.077 5，D1=0.035，密度ρ=1.1×10-9t·mm-3[4].橡胶单元为C3D8R，并进行了网格划分.

1.2 沥青路面有限元模型

有限元模型见图3.半刚性基层沥青路面结构包括上、中、下面层，以及基层、垫层和土基等6个部分.路基尺寸为41.00 m×12.00 m×3.76 m.

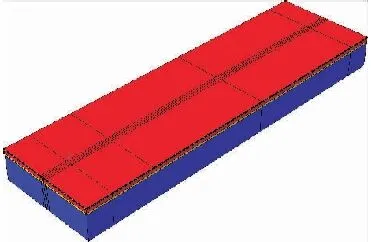
图3 沥青路面有限元模型

沥青混合料黏弹性属性采用Prony级数表示，材料参数见表1[5].黏弹性材料Prony级数参见文献[5].

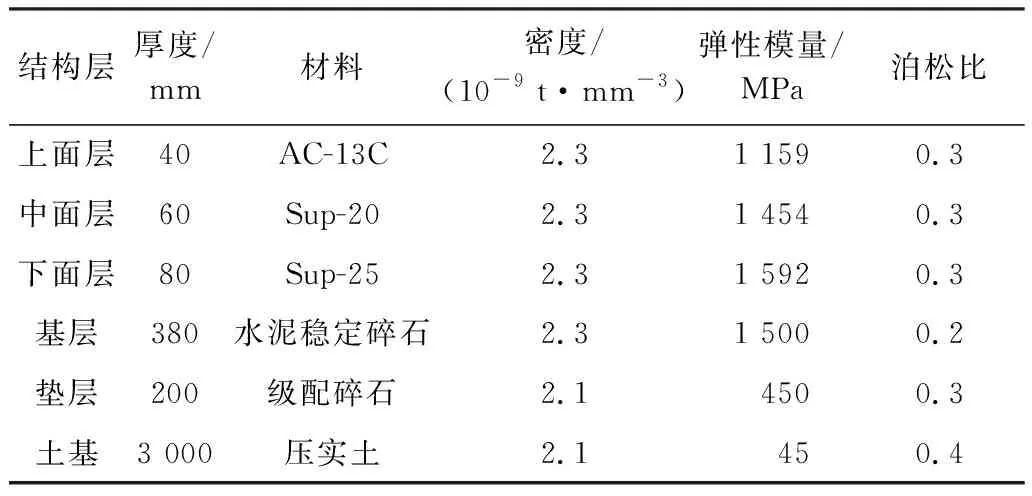
表1 路面材料参数

1.3 Prony级数

采用Prony级数拟合试验曲线可描述沥青混合料黏弹性，公式[6]如下：

(2)

式中：t为时间；G∞和Gi为剪切模量；K∞和Ki为体积模量；τGi和τKi为各Prony级数分量松弛时间.

定义相对模量为

(3)

式中：G0和K0分别为黏弹性材料的瞬态模量，且有

(4)

黏弹性材料泊松比函数为μ=μ(t)，与松弛模量关系为

(5)

式中：E(t)为松弛模量，由试验确定.

E(t)，G(t)和K(t)相应的系数比相同.将G0和K0统一于E(t)形式，松弛模量可表示为Prony级数形式，即

(6)

在G(t)和K(t)中有n′=nG=nK，t=tGi=tKi，α=αGi=αKi.类似于G0和K0，定义瞬态松弛模量及三者关系为

(7)

2 车-路耦合模型

2.1 轮胎-路面接触关系

利用Surface-to-Surface Contact模拟轮胎与路面接触.采用罚函数预测法向力

(8)

式中：Kn为法向接触刚度；C为接触节点相对于目标平面间隙值.

采用库伦摩擦模型预测切向力为

(9)

式中：μ为滑动摩擦因子；Kt为切向刚度；ηe为接触点相对于目标平面弹性变形量.

2.2 轮胎滚动边界条件

当轮胎平动速度小于轮胎切线速度，轮胎驱动前进，接触面摩擦力推动轮胎前进；当轮胎平动速度等于轮胎切线速度，轮胎为自由滚动，此时有

(10)

式中：R，vz和ω分别为轮胎滚动半径、平动速度和角速度.

速度边界条件如图4所示.

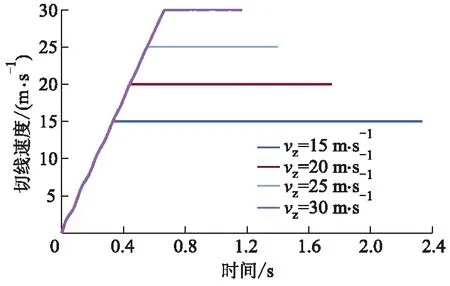
图4 轮胎不同速度边界条件

由图4可知，轮胎由静止达到速度为15，20，25和30 m·s-1时，分别需要时间0.334，0.445，0.554和0.672 s.

3 方程求解

3.1 轮胎滚动方程

轮胎滚动方程[7]为

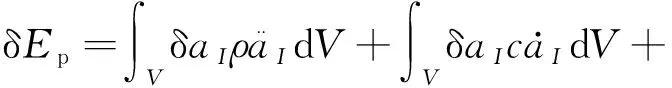
(11)

式中：Ep为总势能；aI为相对于初始构形总位移；I,J=1, 2,3；c为轮胎阻尼；EIJ为格林应变张量；SIJ为第二类Piola-Kirchhoff应力张量；bI为体应力；tI为边界应力.

欧拉坐标和格林应变分别为

x=x(X),

(12)

(13)

其中节点坐标插值、位移插值及位移导数分别为

(14)

式中：α=1,2,…，8;i,I=1,2,3.

格林应变和位移的关系可用应变矩阵B表示：

δE=Bδa.

(15)

离散的虚功原理为

(16)

式中：α,β=1,2,…, 8;i,I=1,2,3.

综上，轮胎滚动动力学方程为

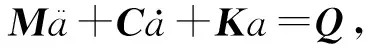
(17)

式中：M，C，K和Q分别为质量、阻尼、刚度和外力矩阵.

3.2 路面不平度

路面不平度功率谱密度[8]为

(18)

式中：n为空间频率；n0为参考空间频率，取n0=0.1 m-1；Gd(n0)为路面不平度系数函数；w为频率指数，一般取w=2.

路面不平度采用余弦叠加法表示，即

(19)

式中：r(z)为路面不平度；z为路面纵向位置；Gq(ni)为功率谱密度函数；θi为[0,2π]区间内随机分布的相位角；Δn为频率增量.

3.3 车-路耦合动力学方程

耦合振动模型可分解为车辆、路面多节点有限元模型，通过轮胎-路面接触耦合，得到动力学方程[9]为

(20)

式中：y，z分别为路面、车辆节点位移向量；Fvr，Frv分别为车轮-路面接触面相互作用力通过形函数分配得到的节点荷载向量；Fvg为车辆自重等效节点荷载列向量.

将车辆、路面视为整体，采用中心差分法求解，获得车辆、路面响应.

4 路面响应分析

4.1 模型验证

将模型分别与文献[10-11]进行对比，如图5，6所示.由图5可知，文献[10]上面层竖向位移为0.392 mm，1/4车辆动载为0.428 mm，误差为9.18%.由图6可知，文献[11]路面中点竖向压应力为0.571 MPa，1/4车辆动载为0.614 MPa，误差为7.53%，表明采用轮胎模型模拟车-路耦合振动可行.

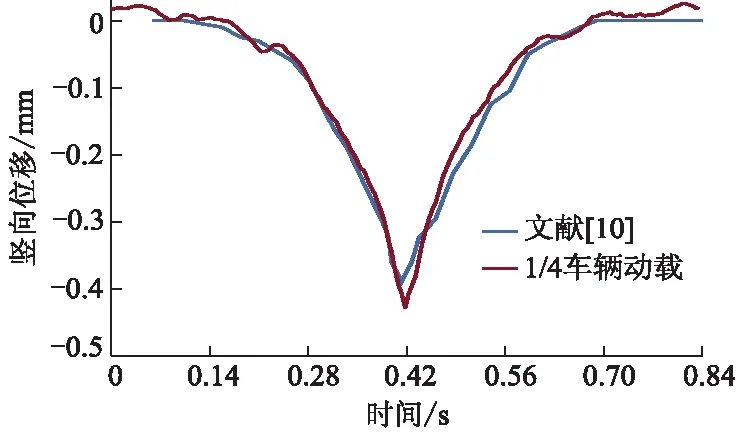
图5 与文献[10]的上面层位移时程曲线对比

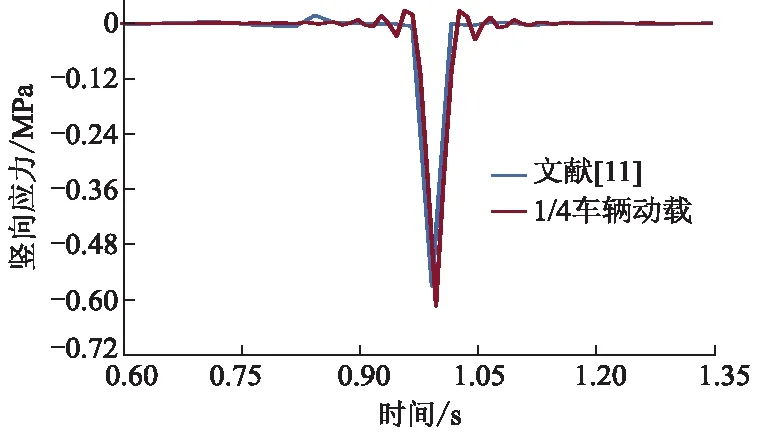
图6 与文献[11]的中面层应力时程曲线对比

4.2 不同作用力对路面响应的影响

取vz=20 m·s-1，F=49 kN.图7为静载与1/4车辆动载作用力时程曲线对比.图8为上面层竖向应力时程曲线对比.由图7，8可知：1/4车辆动载在静载附近上下振动；静载作用下，上面层最大竖向压应力为0.402 MPa，1/4车辆动载为0.563 MPa，比静载增大40.05%.

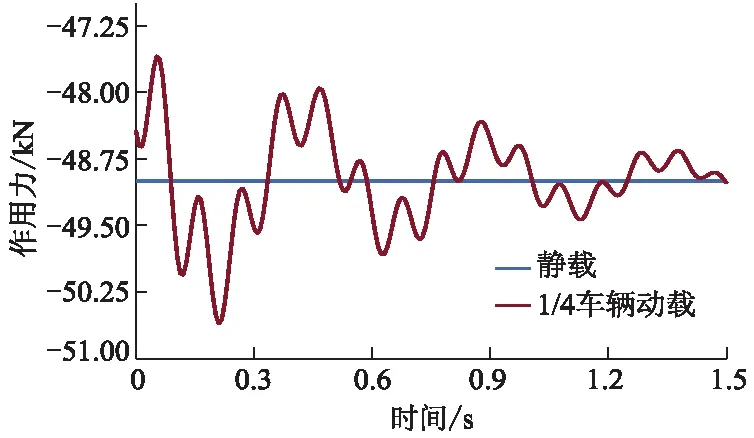
图7 静载与1/4车辆动载作用力时程曲线对比

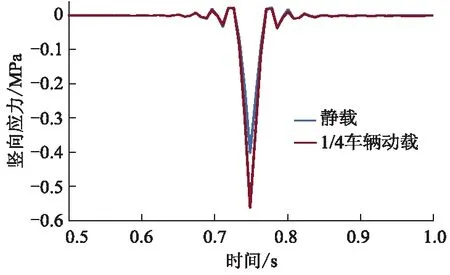
图8 上面层竖向应力时程曲线对比

4.3 不平度对路面响应的影响

图9-11分别为悬架弹力、上面层竖向位移以及上面层竖向应力的时程曲线.

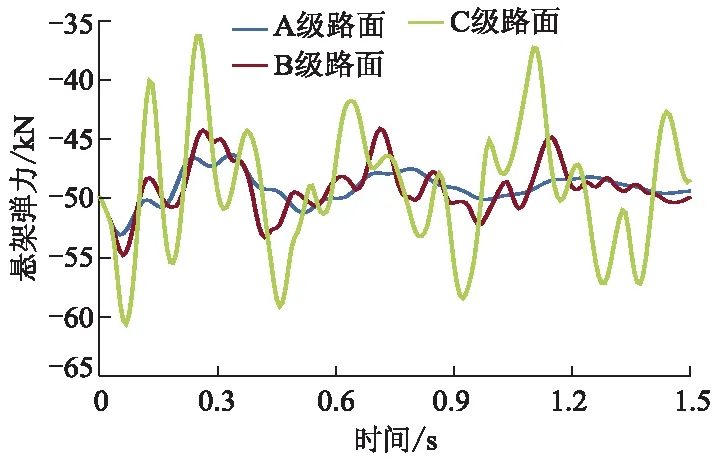
图9 悬架弹力时程曲线

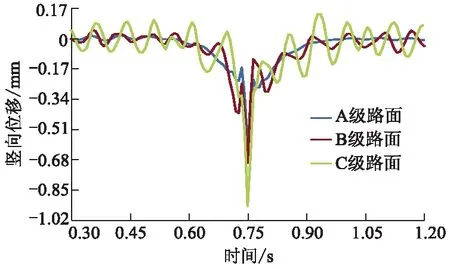
图10 上面层竖向位移时程曲线

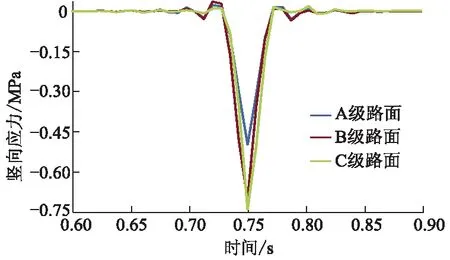
图11 上面层竖向应力时程曲线

由图9-11可知：C级不平度悬架弹力振动较为激烈，B级次之，A级最平缓；A，B和C级路面上面层最大竖向位移分别为0.589，0.698和0.941 mm，C级比A级大59.76%；A，B和C级路面上面层最大竖向压应力分别为0.497，0.702和0.739 MPa，C级比A级大48.69%.

4.4 速度对路面响应的影响

1) 上面层响应分析.图12-15分别为上面层竖向位移、竖向应力、横向应力及纵向应力的时程曲线.

图12 不同车速时上面层竖向位移时程曲线

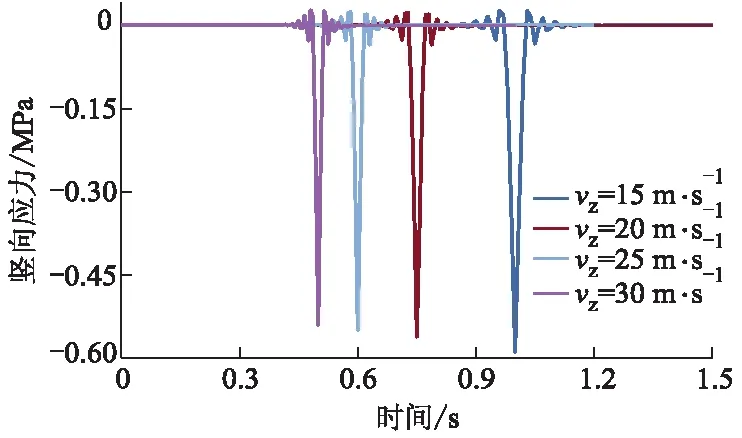
图13 不同车速时上面层竖向应力时程曲线

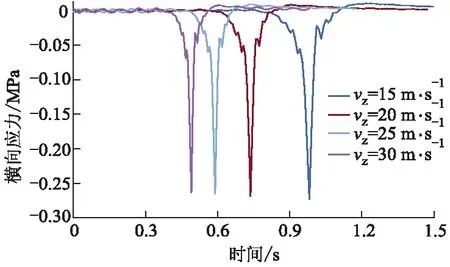
图14 不同车速时上面层横向应力时程曲线

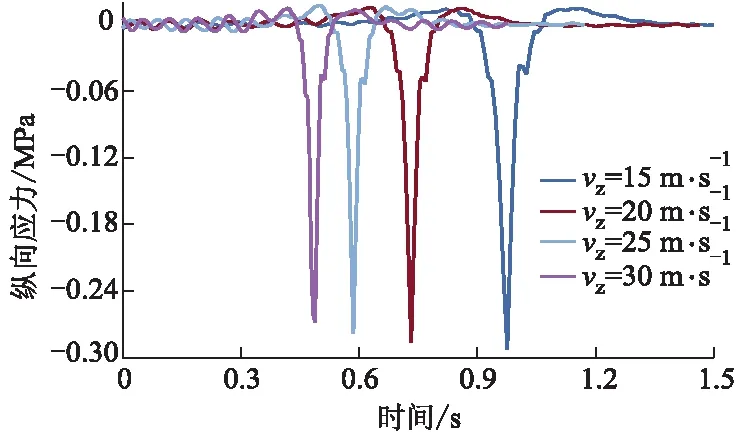
图15 不同车速时上面层纵向应力时程曲线

由图12-15可知：车速为15，20，25和30 m·s-1时，上面层竖向位移峰值分别为0.705，0.665，0.641和0.607 mm，最大竖向压应力分别为0.591，0.563，0.550和0.542 MPa，最大横向压应力分别为0.273，0.268，0.265和0.264 MPa，最大纵向压应力分别为0.292，0.286，0.278和0.268 MPa；车速越快，竖向位移和应力均减小.

图16-17分别为轮胎接地Mises应力云图和纵向切应力云图.

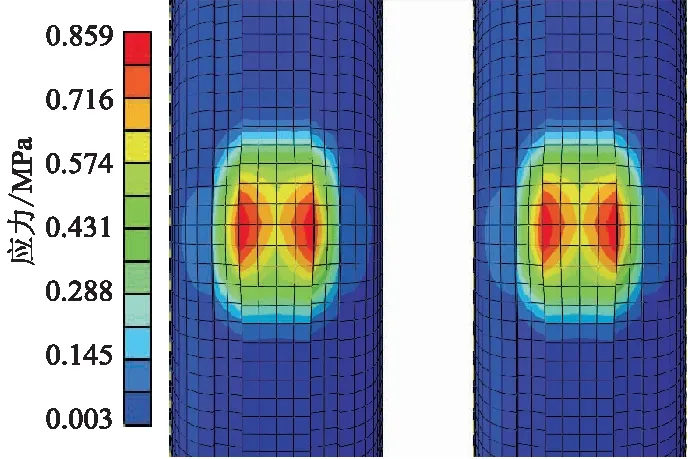
图16 Mises应力云图

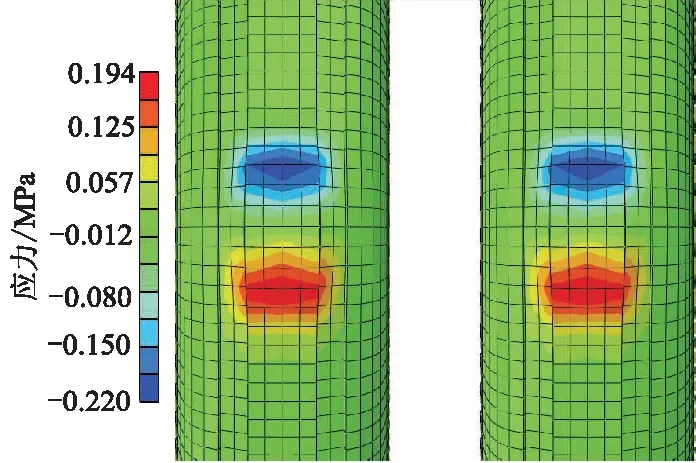
图17 纵向切应力云图

由图16，17可知：接地Mises应力对称显示，高应力分布在胎肩两侧；纵向切应力最大值和最小值为前后分布.

2) 路面各层响应分析.选取vz=15 m·s-1分析各层响应，图18为竖向位移时程曲线.图19-21为三向应变时程曲线.由图18可知，各层竖向位移峰值分别为0.705，0.514，0.498，0.346，0.398和0.289 mm.由图19可知：各层竖向压应变分别为-4.275×10-4，-4.255×10-4，-1.588×10-4，-6.210×10-5和-1.520×10-4，拉应变分别为7.25×10-5，7.93×10-5，2.86×10-5，1.00×10-6，3.50×10-6；中面层出现最大压应变，下面层出现最大拉应变.

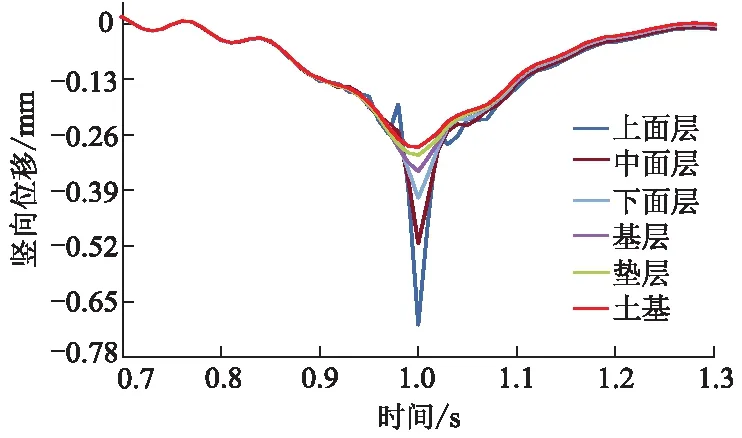
图18 各层竖向位移时程曲线

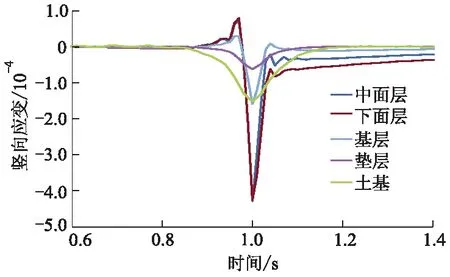
图19 各层竖向应变时程曲线

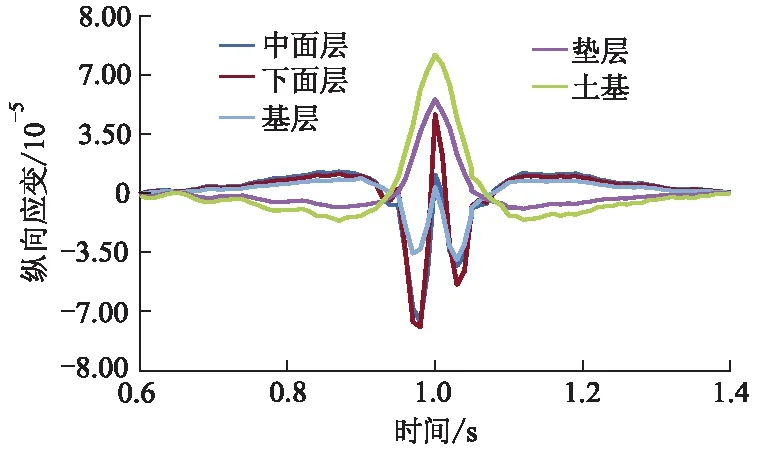
图20 各层纵向应变时程曲线

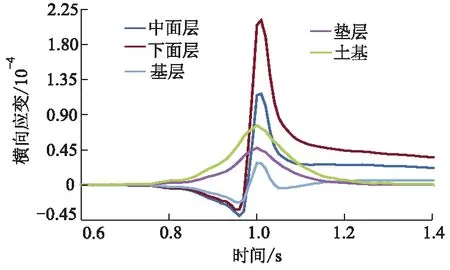
图21 各层横向应变时程曲线

由图20可知：各层纵向压应变分别为-7.62×10-5，-7.94×10-5，-3.95×10-5，-9.29×10-6，-1.64×10-5，拉应变分别为1.28×10-5，4.65×10-5，8.93×10-6，5.55×10-5，8.18×10-5；下面层出现最大压应变，土基出现最大拉应变.

由图21可知：各层横向压应变分别为-3.95×10-5，-3.16×10-5，-2.22×10-5，-1.50×10-7，-2.70×10-7，拉应变分别为1.170×10-4，2.113×10-4，2.830×10-5，4.760×10-5，7.640×10-5；中面层出现最大压应变，下面层出现最大拉应变.

4.5 轴荷对路面响应的影响

选取vz=15 m·s-1分析轴荷对路面响应的影响，图22-23分别为轴荷与上面层竖向位移、竖向应力关系曲线.由图22-23可知，轴荷增加300.00%，上面层竖向位移增加222.89%，竖向应力增加了337.26%.

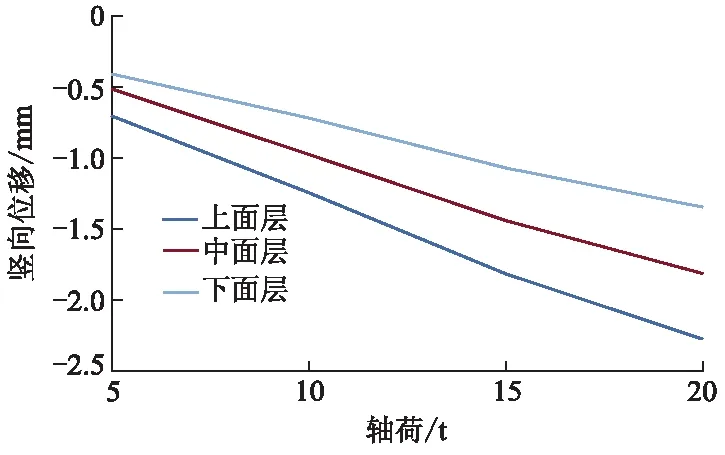
图22 轴荷与上面层竖向位移关系曲线

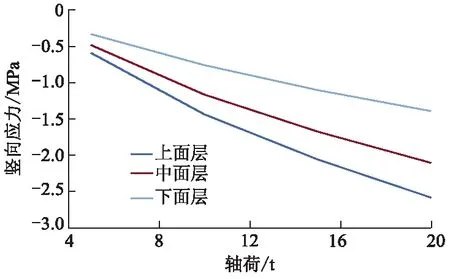
图23 轴荷与上面层竖向应力关系曲线

5 结 论

1) 与相关文献对比，表明本研究中的模型合理；静载作用下上面层最大竖向压应力为0.402 MPa，1/4车辆动载为0.563 MPa，比静载增大40.05%，表明研究车-路耦合振动时，如果忽略车辆动载，结果存在较大偏差.

2) 车速越快，响应越小；接地Mises应力对称分布显示，高应力分布在胎肩两侧；纵向切应力最大值和最小值为前后分布.

3) 竖向位移随路面深度增加而减小；下面层出现最大竖向拉应变；土基出现最大纵向拉应变；下面层出现最大横向拉应变；随着轴荷增加，面层竖向位移、竖向应力均增大.