废水处理过程的KPLS-GPR软测量建模

刘鸿斌， 杨 冲

(南京林业大学 江苏省林业资源高效加工利用协同创新中心， 江苏 南京 210037)

在造纸废水处理过程中，往往存在着大量难以测量或无法在线测量、且密切影响着出水指标控制的参数，被称作主导变量，如化学需氧量(chemical oxygen demand, COD)和悬浮固形物(suspended so-lids, SS)等.为提高造纸污水处理的达标率，提升系统的稳定性，需要对这些主导变量进行及时监测.传统传感器测量方法普遍存在成本高、维护难、稳定性能差和使用寿命短等问题.相比之下，软测量技术以建模简单、方法多样及预测效果可观等优势，为精确的数据测量提供了较好的选择.在软测量模型中，基于数据的软测量模型旨在挖掘潜在信息，以解释数据特征，更适合工业过程预测，主要包括回归分析模型、人工智能模型与潜变量模型等.

多元线性回归(multiple linear regression, MLR)是回归分析中基本的统计分析方法，适用于多种因素关联的变化结果，其分析的技术核心是最小二乘法，属于线性方法，不适于复杂非线性的造纸废水处理过程建模.人工智能模型中的人工神经网络(artificial neural network, ANN)和支持向量机(support vector machine, SVM)应用较为广泛，属于非线性处理方法.在废水处理领域，HUANG M.Z.等[1]将基于遗传算法的模糊神经网络应用于生物污水处理中养分浓度的实时估计.汪瑶等[2]使用ANN和最小二乘支持向量机(least square support vector machine, LSSVM)对出水COD和SS含量进行了软测量建模，并比较了两种方法的优劣.在其他工业领域，J. C. B. GONZAGA等[3]采用ANN完成了对于聚对苯二甲酸乙二酯黏度的在线估计，为进行实时工艺控制提供了有效方案.LIU H.B.等[4]采用即时学习技术提高了最小二乘支持向量机对地铁内PM2.5含量的预测效果.不同于以上两种非线性方法，高斯过程回归(gaussian process regression, GPR)用来描述函数的分布问题，C. E. RASMUSSEN等[5]将其应用于机器学习.具有易实现、灵活的非参数推广及超参数自适应调节等优点，可以对预测输出变量做出概率解释[6].此外，GPR还可通过对核函数进行组合的方式，使模型具备不同的函数特性[7].因此，对于数据特征较为复杂的造纸废水处理过程，GPR具有很大优势.宋留等[8]采用核函数相加的方式构建GPR模型，对造纸废水处理过程中的出水指标进行预测，结果显示高斯过程回归模型的预测效果优于多元线性回归、主成分回归、偏最小二乘回归及人工神经网络等常规软测量模型.

潜变量模型的优点在于，经过模型分解与参数选择，潜变量不仅包含对数据的解释，而且具备低维度与独立正交关系，因此可有效减弱原始工业数据对于模型预测结果的不利影响.常用的潜变量模型有主成分分析法(principal component analysis, PCA)、偏最小二乘法(partial least squares, PLS)和典型相关分析法(canonical correlation analysis, CCA)[9-10].在基于潜变量模型的软测量模型中，XIE B.等[11]将PCA-LSSVM与非支配排序遗传算法结合，用于完成氨浓度与总氮浓度的预测，以更好地控制废水处理中厌氧氨氧化过程.刘鸿斌等[12]采用基于PCA主成分的ANN与LSSVM软测量模型，对造纸废水处理过程中的出水COD和SS含量进行预测，结果显示PCA-ANN与PCA-LSSVM模型在预测性能上优于常规模型.

上述方法中，虽然潜变量模型的应用均有积极效果，但并未考虑到监督型潜变量方法的建模效果.PCA主成分的提取来自于对输入数据X的分析，与输出数据Y无关，因此，无法确保根据特征值降序排列所提取的PCA主成分对于Y是否具有最佳解释效果.而PLS和CCA在概括自变量系统信息的同时，注重要求所提取的得分向量对输出数据Y的解释能力，因此更具备质量相关特性.此外，相比于CCA，PLS在确保X与Y相关性的同时，也注重对于数据方差结构的解释，在潜变量模型中的应用最为广泛.

常规的潜变量模型均为线性方法，面对非线性数据缺乏一定的解释能力.近年来，核方法的应用为潜变量模型提供了更大的应用空间，包括故障检测、故障重构及故障分析等[13].对于预测模型的构建，WANG M.Y.等[14]将核偏最小二乘(kernel partial least squares, KPLS)运用于两种非线性案例，验证了KPLS对于数据预测的高效性.HUANG X.等[15]根据线性PLS回归过程中的变量贡献率优化了KPLS模型，提高了模型预测能力.从理论上讲，KPLS预测模型完成了两个步骤：首先，经非线性映射，将输入数据转移至高维特征空间，使得非线性特征更易被模型提取；其次，完成高维特征空间数据与输出数据的线性PLS拟合.因此，KPLS的潜变量既保持了常规潜变量对于数据维度和结构的优化，同时提升了对非线性数据的解释能力.

基于KPLS潜变量与GPR的优点，采取KPLS-GPR模型对造纸废水处理过程进行软测量建模，分别完成对于出水COD和SS含量的预测.此外，引入常规的潜变量方法(PLS)与预测模型(ANN)作为对比元素，以验证KPLS-GPR模型的预测能力.

1 KPLS潜变量模型

KPLS的构建可分为两步：首先通过非线性映射将输入变量映射到高维特征空间，其次建立高维变量与输出变量间的线性PLS模型.根据Cover定理，原始数据中的非线性特征在高维空间中可能呈现线性特征.因此，经模型分解，KPLS的潜变量可对数据的非线性特征具备更高的解释能力.

假设输入矩阵X=[x1,x2,…,xn]T∈Rn×m包含n个测量样本，m个过程变量；输出矩阵Y=[y1,y2,…,yn]T∈Rn×s包含n个测量样本，s个过程变量.输入数据xi经非线性映射，可表示为φi=Φ(xi)，则高维特征空间内两个变量的内积可使用核技巧表示[10]：

(1)

式中：xi和xj为输入变量，i，j=1,2,…,n；K(x)为核函数.

在不同种类的核函数中，较为常用的为高斯径向基函数(radial basis function, RBF)，即

(2)

式中：σR为核函数宽度.

基于此，所有输入数据在特征空间中可表示为

φ(X)=(φ(x1),φ(x2),…,φ(xn))T.

(3)

则特征空间数据的內积可以由n×n的Gram矩阵代替：

(4)

KPLS的模型分解可表示为

(5)

式中：T为K的得分矩阵，T=[t1,t2,…,td]∈Rn×d；U为Y的得分矩阵，U=[u1,u2,…,ud]∈Rn×d；P和Q分别为K和Y负载矩阵，P=[p1,p2,…,pd]∈Rm×d，Q=[q1,q2,…,qd]∈Rp×d；E和F分别为K和Y的残差矩阵；d为KPLS的潜变量的个数.

使用非线性迭代最小二乘法(non-linear iterative partial least squares, NIPALS)可以完成模型求解，具体步骤可参考文献[16].

2 预测模型

2.1 GPR建模原理

假设输入矩阵为X=[x1,x2,…,xn]T∈Rn×m，模型输出值为y∈Rn×1，n为样本量，m为变量个数.由于高斯过程是任意有限个具有联合高斯分布的函数集合[5]，因此可表示为

f(x)～GP(m(x),C(x,x′))，

(6)

式中：m(x)为均值函数；C(x,x′)为协方差函数.

由于数据标准化后均值为0，因此高斯过程可简化为

f(X)～GP(0,C(xi,xj))，

(7)

式中：i,j=1,2,…,n.

将噪声考虑到观测目标值中，考虑如下的回归模型：

y=f(X)+ε，

(8)

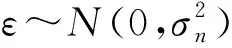
(9)

观测值y与预测值y*的联合先验分布为

(10)

式中：X为输入训练集；X*为输入测试集；C(X,X*)代表着训练集X与测试集X*样本点间的协方差矩阵，C(X,X*)=C(X*,X)T；C(X*,X*)为测试集X*样本自身的协方差矩阵；In为n维单位矩阵.

由此，高斯过程回归的预测值可表示为

(11)

其中，

(12)

(13)

预测点的均值与方差分别用来计算预测值和对应的置信区间[6].

2.2 协方差函数

高斯过程回归可以选择不同的协方差函数进行预测，以下介绍3种协方差函数[5]：

1) 平方指数协方差函数(squared exponential covariance function, SE),即

(14)

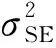
2)线性协方差函数(linear covariance function, L)，即

(15)

3)周期性协方差函数(periodic covariance function, P)，

CP(xi,xj)=C0(u(xi),u(xj))，

(16)

式中：C0为任意随机核函数.

周期性协方差函数将一维输入变量映射到二维u(x)空间，从而得到关于x的周期性随机函数：

(17)

式中：p为周期参数.

若C0=CSE，则Cp可以转化为

(18)

2.3 协方差函数的组合

高斯过程允许组合不同的协方差函数产生新的协方差函数，文献[7]将协方差函数累加的方式视作逻辑“或”运算.通过协方差函数相加的方式组成的高斯过程，可视为具备不同结构独立函数的累加过程.因此，组合后高斯过程具备丰富的模型结构和较强的数据解释能力.假设f1，f2相互独立，并符合分布f1～GP(u1,k1)，f2～GP(u2,k2)，则两个函数相加可表示为f=f1+f2～GP(u1+u2,k1+k2).

2.4 超参数的获取

超参数的集合一般通过最大似然法求得，即

(19)

3 基于潜变量的软测量建模过程

基于潜变量的软测量建模流程如图1所示.图中ρ(COD)in和ρ(COD)eff分别为进、出水的COD质量浓度；ρ(SS)in和ρ(SS)eff分别为进、出水的SS质量浓度；Q为流量；t为温度；ρ(DO)为DO的溶解氧质量浓度.该流程图包括以下4个部分：① 完成数据的标准化与预处理； ② 构建KPLS模型，对样本数据进行分解，完成得分矩阵T的选取； ③ 建立所述得分矩阵T与输出数据Y的GPR预测模型； ④ 根据输出数据的预测值与测量值，计算出均方根误差(RMSE)与决定系数(R2)，完成对KPLS-GPR模型预测能力的评估.

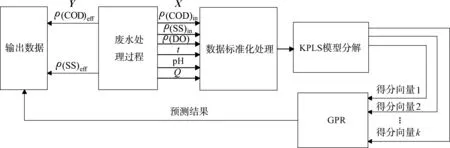
图1 基于KPLS潜变量的软测量流程图

RMSE和R2表示如下：

(20)

(21)

RMSE越接近于0，代表该模型预测试验数据具有更高的精确度.R2的结果一般在0到1之间，R2越接近1，拟合程度越高.

4 仿真试验与讨论

为验证模型的预测能力，仿真试验基于造纸废水数据，分别完成对出水COD和出水SS质量浓度的数据预测.此外，建立常规预测模型(ANN和GPR)、基于PLS的潜变量模型(PLS-ANN和PLS-GPR)以及基于KPLS的潜变量模型(KPLS-ANN和KPLS-GPR)，完成预测能力的对比.

4.1 造纸废水数据采集与处理

造纸废水数据取自广东省东莞市某造纸厂好氧段废水监测数据.取样间隔2～3 d.数据包括8个废水变量，每个变量包括170个测量值[17].造纸废水处理过程数据如图2所示.对数据进行预处理后，共有162个测量数据用于仿真试验，其中前100个测量样本为训练集，后62个测量样本作为测试集.预测模型的输入端包括ρ(COD)in，ρ(SS)in，ρ(DO)，Q，t和pH等6个变量；ρ(COD)eff和ρ(SS)eff为输出端变量.

图2 造纸废水处理过程数据

4.2 预测模型

4.2.1常规预测模型

使用软测量模型进行数据预测前，需对模型参数进行调整，以取得最优预测结果.ANN模型的网络总层数为3层，包含1个输入层、1个隐含层和1个输出层，其中输入层节点数为6个，隐含层节点数为3个，输出层节点数为1个.隐含层采用tan-sigmoid激活函数，输出层采用purelin激活函数.对于GPR模型，采取CSE+L+P(见2.3部分)作为协方差函数，使用最大似然法求得7个最优超参数.

4.2.2基于PLS潜变量的预测模型

表1列出了采用PLS建模时，不同潜变量个数对方差贡献率以及累计贡献率的影响.由表1可知：输入数据的累计方差贡献率，在潜变量个数超过3个后变化趋于平缓；输出数据的累计方差贡献率，在潜变量个数超出3个后无明显变化.故选择前3个潜变量作为预测模型的输入较为合适.此外，PLS-GPR预测模型中GPR核函数选取和参数选择方式与4.2.1部分相同；由于潜变量的选择，PLS-ANN的输入层节点变为3个，其余的网络结构与ANN保持一致.

表1 PLS模型潜变量的方差贡献率及累计贡献率 %

4.2.3基于KPLS潜变量的预测模型

不同于PLS模型，KPLS模型分解建立在经非线性映射后的高维特征空间.具体而言，KPLS模型的核函数采用高斯径向基函数，核宽为7.75.此外，采取表1中的潜变量选取方式，KPLS模型选取前4个潜变量构建预测模型.KPLS-GPR预测模型中GPR核函数选取和参数选择方式与4.2.1部分的选取方式相同.由于潜变量的选择，KPLS-ANN的输入层节点个数变为4个，其余网络结构与ANN保持一致.表2为KPLS-ANN和KPLS-GPR的具体潜变量模型参数.

表2 基于KPLS的潜变量模型参数

4.3 结果与讨论

结合以上的参数设置与模型调整，表3和表4分别列出了不同预测模型对于出水COD和SS质量浓度的预测结果.

表3 不同预测模型对出水COD质量浓度的预测结果

由表3可知：通过对测试集出水COD质量浓度的预测，ANN的RMSE为4.794 mg·L-1，R2为0.420；GPR的RMSE为4.559 mg·L-1，R2为0.475，预测精度相对较高.结合PLS潜变量后，常规模型的预测效果均有所提高，PLS-ANN的RMSE和R2分别为4.665 mg·L-1和0.451，PLS-GPR分别为4.490 mg·L-1和0.491.PLS-GPR在PLS潜变量预测模型中具备较优预测效果，R2相比于GPR提高3.37%.在PLS潜变量预测模型的基础上，KPLS潜变量预测模型对测试集COD质量浓度的预测效果有更进一步的提升.KPLS-ANN的RMSE和R2分别为4.559 mg·L-1和0.476，R2较PLS-ANN提升5.54%；KPLS-GPR分别为4.102 mg·L-1和0.575，R2较PLS-GPR提升17.11%.可见，在6种模型中，KPLS-GPR对测试集出水COD质量浓度具备最优预测效果，相比于常规的预测模型，R2提升最多，提升了36.90%.

表4 不同预测模型对出水SS质量浓度的预测结果

由表4可知：GPR，PLS-GPR和KPLS-GPR在常规预测模型、PLS潜变量预测模型和KPLS潜变量预测模型中分别具备较优预测结果，其中KPLS-GPR预测精度最高，PLS-GPR次之，GPR最低.相比于PLS潜变量，KPLS潜变量对常规模型的预测效果提升更为明显.以R2为准，KPLS-GPR的预测效果较GPR提升7.21%，PLS-GPR较GPR提升2.11%，KPLS-ANN较ANN提升16.51%，PLS-ANN较ANN提升7.78%.对测试集出水SS质量浓度的预测，最优模型KPLS-GPR的RMSE为0.656 mg·L-1，R2为0.610，相比于常规的预测模型，R2提升最多，为43.87%.总之，KPLS潜变量预测模型对输出变量均具备相对较好的预测结果.图3-6分别为KPLS-ANN和KPLS-GPR对出水COD和SS质量浓度的预测.

图3 KPLS-ANN对出水COD质量浓度预测结果

图4 KPLS-ANN对出水SS质量浓度预测结果

图5 KPLS-GPR对出水COD质量浓度预测结果

图6 KPLS-GPR对出水SS质量浓度预测结果

KPLS潜变量对常规预测模型存在较为显著的优化，主要原因在于：经过非线性映射，数据原始的非线性特征在高维特征空间中更易被提取，故KPLS潜变量较常规PLS具备更高的数据解释能力；通过选取合适的潜变量作为预测模型的输入，可有效消除特征空间的高维度“灾难”；潜变量的独立性可优化数据结构，减少共线性对预测模型的影响.对于预测模型，由于协方差函数的组合，GPR模型在一定程度上可视为多种独立函数的叠加，因此具备同时解释多类数据特征的特点.试验结合造纸废水数据的非线性特征、采样的周期性以及较为有限的样本量，采取平方指数协方差函数、周期性协方差函数以及线性协方差函数的相加的方式构建组合协方差函数，使得GPR模型较ANN模型具备更强的建模能力.因此，KPLS潜变量与GPR模型的结合，使得模型具备最优预测效果.

5 结 论

采用KPLS-GPR模型对造纸废水数据中的出水COD和SS的质量浓度进行预测.首先，采用KPLS的潜变量作为GPR模型的输入端，在降低数据的维度与优化数据结构的同时，提供了对于数据非线性特征的充分解释.其次，GPR模型对于数据结构的考虑，使得模型适用于复杂多变的造纸废水处理环境.因此，KPLS-GPR较常规模型可取得更优的预测结果.此外，潜变量对输入数据的预处理对于其他流程工业(钢铁、化工等)的大数据建模也提供了相应的优化思路.