基于VMD-AR谱的多轴转子系统故障特征信息提取方法

吴 飞， 程 科， 丁 军， 刘苏行

(武汉理工大学 机电工程学院， 湖北 武汉 430000)

多轴转子系统是一种多应用于大型船舶推进系统、汽轮机转子和航空发动机等大型旋转机械的典型转子模型[1]，其工作状态的稳定关乎经济效应和生命安全.多轴转子系统是大型旋转机械的重要部件，容易在运行过程中发生多种故障，主要故障有转子不平衡、转轴不对中、转子系统松动等.一旦发生故障，轻则导致大型旋转机械效率降低或者停机，重则导致整个生产线无法正常工作，甚至造成人员伤亡.所以，在设备运行过程中，对多轴转子系统的运行状态进行监测和特征信号的特征信息提取可以保障设备的安全运行，有利于增强大型旋转机械运行的安全性和稳定性，对保障生产的安全具有重要意义.

当多轴转子系统出现故障时，故障位置相互接触的元器件会随着系统旋转，形成周期性的冲击力，产生非线性、非稳定性的特征信号[2].针对双跨转子试验平台的振动信号，EEMD(ensemble empirical mode decomposition)可以有效地抑制模态混叠现象[3]，但是无法区分近频部分的模态混叠.DING J.等[4]通过VMD(variational mode decomposition)将齿轮故障振动信号分解为几个IMFs(intrinsic mode functions)，并提取每个IMF的样本熵值，以形成后续故障诊断的特征向量.VMD构造了一组变分Wiener滤波器[5]，可以有效抑制近频部分的模态混叠，且表现了较好的鲁棒性[6].分解出的IMFs采用Hilbert边际谱进行特征提取，但是边际谱容易产生峰值重叠，故障特征难以分辨[7].

针对Hilbert变换的局限性，文中提出VMD和AR(autoregressive)谱相结合的方法，对非线性、非稳态振动信号进行分析，利用瞬时频率均值法选取分解模式数k，避免k值的经验选取；AR模型克服了Hilbert分离算法存在的加窗效应，在频带划分上具有较强的分辨率.AR谱利用不同特征信息对IMFs进行特征频带划分，可以有效地进行故障特征提取，并为改进的粒子群优化算法的混合核支持向量机算法提供特征信息，便于准确地识别故障模式[8].

1 基本理论分析

EMD和EEMD在近频部分都会产生不同程度的模态混叠，VMD采用递归循环分解信号处理方式，可以有效抑制近频部分的模态混叠.

1.1 变分模态原理

采集的信号常包含噪音，该信号可以表示为

fo=f+η，

(1)

式中：f为原始信号；η为加入的高斯白噪声.

为了复原真实的原始信号f，使用Tikhonov正则化原理将f最小化[9]为

(2)

为了评估模式的带宽，受约束的变分问题被表述为

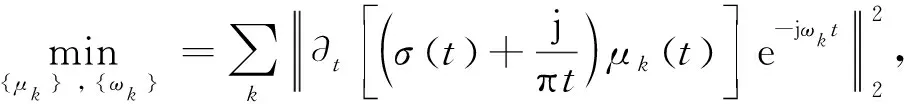
(3)

式中：{μk}={μ1,μ2,…,μk}代表分解的IMFs；{ωk}={ω1,ω2,…,ωk}代表分量信号的中心频率.引入二次惩罚项和拉格朗日算子λ求解增广拉格朗日函数，使得各分量的带宽和最小，基于交替方向乘子法，将增广拉格朗日函数分解成3个子问题μk,ωk,λk，通过不断迭代求取μk,ωk,λk的最优解，最后整合获得原函数的最优分解，表达式为

(4)

(5)

(6)

式中：τ为噪音容限参数.当相对误差e小于收敛容差ε，则VMD过程停止，且e的计算式为

(7)

1.2 分解模式数

在现有的时域信号分解方法中，分解模式数k是一个极其重要的因素，k值选取较小，则会遗漏某些重要的分量信号IMF，无法准确反映信号的整体信息；k值选取较大，则引起VMD的过度分解，信号变得间歇，使得分量信号偏离原始信号的真实含义，同时也会导致运算时间过长，产生的分量信号较多，对于提取分量信号的特征造成一定的干扰.

VMD在算法上实现了k值可选，但是k值的选取并没有一个确定的依据.在实际应用过程中，需要根据人工经验，反复尝试不同的k值，寻求最优分解.文中根据VMD分解分量信号的瞬时频率均值，提出一种改进的VMD方法，用来评估VMD分解模式数k的确定.

1.3 瞬时频率均值

VMD方法将给定信号分离成k个IMF分量，步骤如下：

1) 分量信号的Hilbert变换：

(8)

式中：P为柯西主值，舍弃在τ=t以及τ=±∞处的奇点，一般取P=1.

2)构造解析信号：

(9)

式中：ai(t)为瞬时幅值函数；φi(t)为瞬时相位函数.

3)计算瞬时频率：

(10)

式(10)可以计算每一个IMFci的瞬时频率，定义瞬时频率的均值为M，并将其用作筛选IMF分解模式数的终止标准，即

(11)

式中：fi为各个分量信号的瞬时频率；Pi为fi出现的概率.将信号以不同k值进行分解，观察瞬时频率均值与k值的关系.随着分解个数增大，在高频部分，瞬时频率均值越来越低，曲率变化明显，表明分解模式数k值过大，无法准确表征原信号信息，因此以刚好不发生明显曲率明显变化的k值作为理想值进行信号分解.

构建一个仿真信号x(t)=(2+e2t)sin(2π×80t)，调制信号是80 Hz的基本信号，将构建的信号按照VMD分解成较多的IMFs分量信号，针对各个分量信号进行均值计算，VMD分解的前9个分量信号的瞬时频率如图1所示.

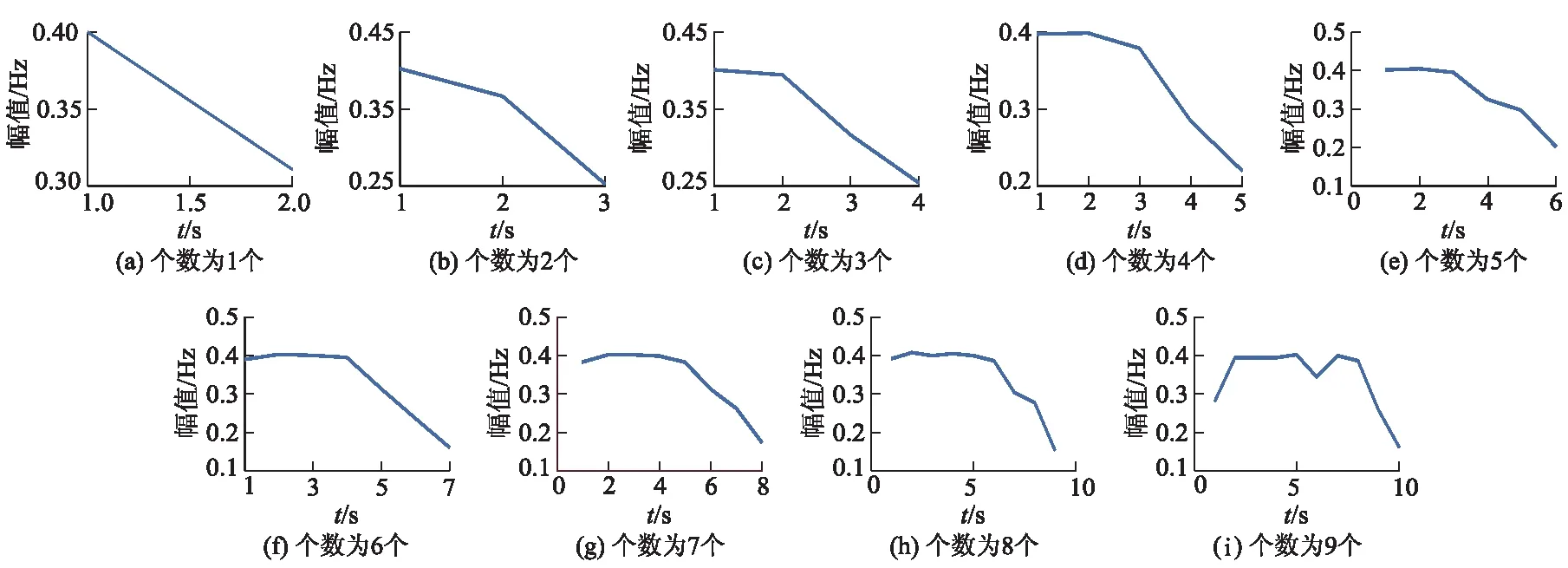
图1 瞬时频率平均曲线

如图1所示，通过这9个特征曲线，借助曲率进行量化分析，当分量的个数持续增加时，明显观察到瞬时频率的均值曲线具有明显向下的弯曲现象，定义此时刚好不发生弯曲的分解个数为临界k值.当分解个数为2个时，均值曲线有明显的向下弯曲，故k取1.

2 AR谱特征提取

时变参数模型可以对设备的运行状态进行预测，具有较高的预测精度，但是其计算量大，使用常常受到较大限制.针对时变参数模型对故障诊断的局限性，提出VMD与AR谱相结合的方法，既解决了时变参数模型对故障信号直接诊断的不准确性，又克服Hilbert分离算法的局限性，解决了Hilbert-Huang变换中产生的边际谱峰值混叠、故障难以分辨的问题.VMD方法在时域内将复合信号分解为若干个均值为0且具有确定频率IMF分量.AR模型是时间序列模型，表征系统的特征和工作状态，在时间轴上也可以用来外延故障特征信息，可以使用AR模型参数对设备进行诊断，还可以对故障隐患进行早期预测.VDM-AR将复合信号进行时域内的VMD分解，进而采用AR谱进行分量信号的特征提取.AR模型表达式为

(12)

式中：y(n)为自回归时间序列;V(n)为关于方差e2的正态分布;N为模型的顺序.

3 多轴转子系统故障特征提取

3.1 VMD-AR流程

试验采用搭载多轴转子系统的试验台，如图2所示，通过弹性联轴器对多个传动轴连接，允许各个轴段有一定角度的偏移，以此模拟轴系系统的不对中、不平衡和松动故障.搭建转子数据采集试验台，如图3所示，该试验台采用NI PXIe-4492振动数据采集模块对振动信号进行采集，通过三轴加速度传感器和电涡流位移传感器采集数据，并对数据进行卡尔曼滤波和通过信噪比进行融合[10].

VMD-AR流程如下：

1) 振动信号采集.诊断对象为多轴转子系统，如图2所示，设计搭建转子信号采集试验台如图3所示，设置采样频率为1 000 Hz，采样点数为1 000个.

图2 多轴转子系统

图3 转子系统数据采集试验台

2) 选取合适分解模式数k.依据文中瞬时频率均值法选取适合的k值.

3) VMD分解.在时域内对系统信号进行分解为k个分量信号.

4) VMD-AR谱分析.对分解的所有IMF进行AR谱分析，分别对比后进行能量累加，提取故障特征.

3.2 VMD-AR数据处理

对转子试验台进行故障模拟，并在给定的转速情况下，利用加速度传感器采集试验台的振动信号.对所得数据进行瞬时频率均值提取，如图4所示，得分解模式数k=4.

图4 分解模式数确定

不同工况下采集的多轴转子试验台信号时间-幅值图如图5所示.图6-9分别为多轴转子试验台在正常、转子不对中、转轴不平衡和系统松动4种不同工况下，分解模式数k=4的VMD分解IMFs图.

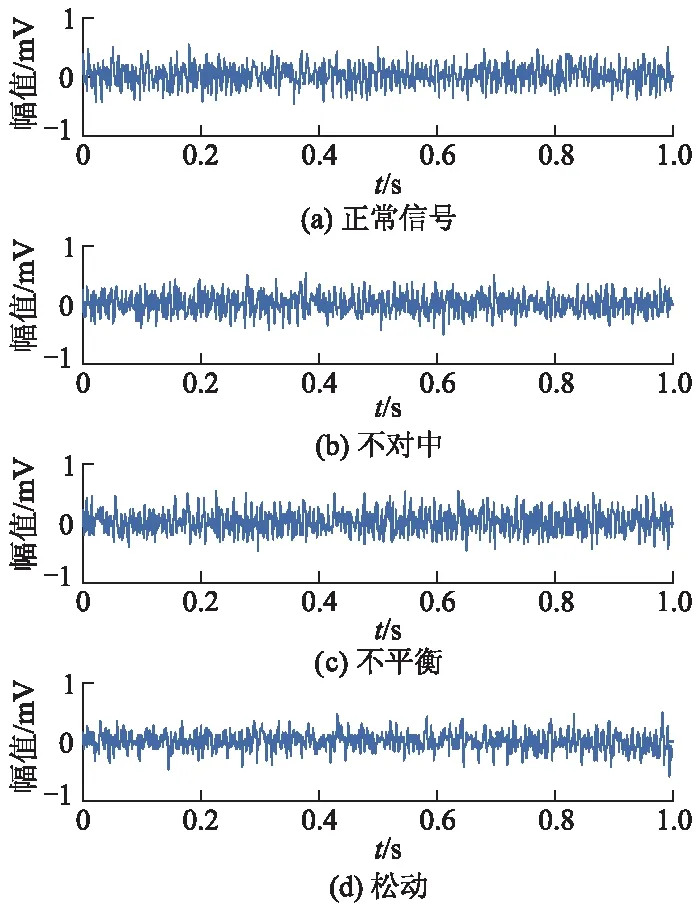
图5 转子试验台不同工况下的原信号

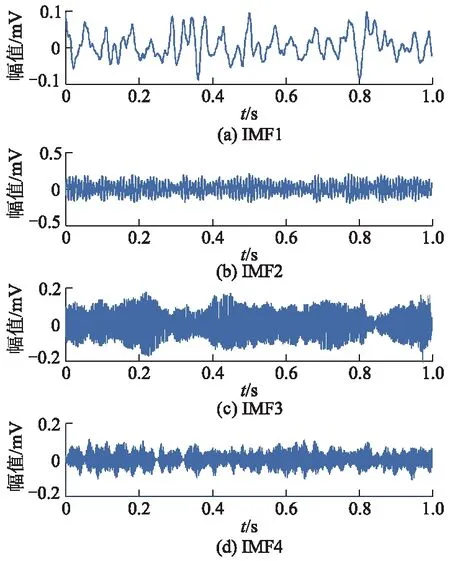
图6 正常信号的VMD分解

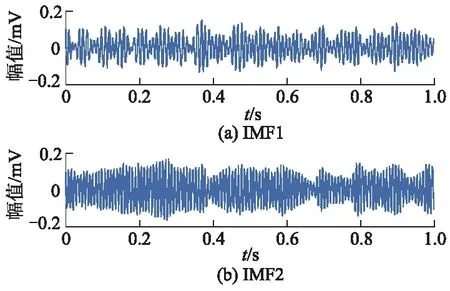
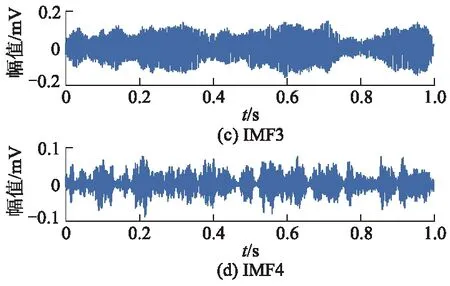
图7 不对中信号的VMD分解

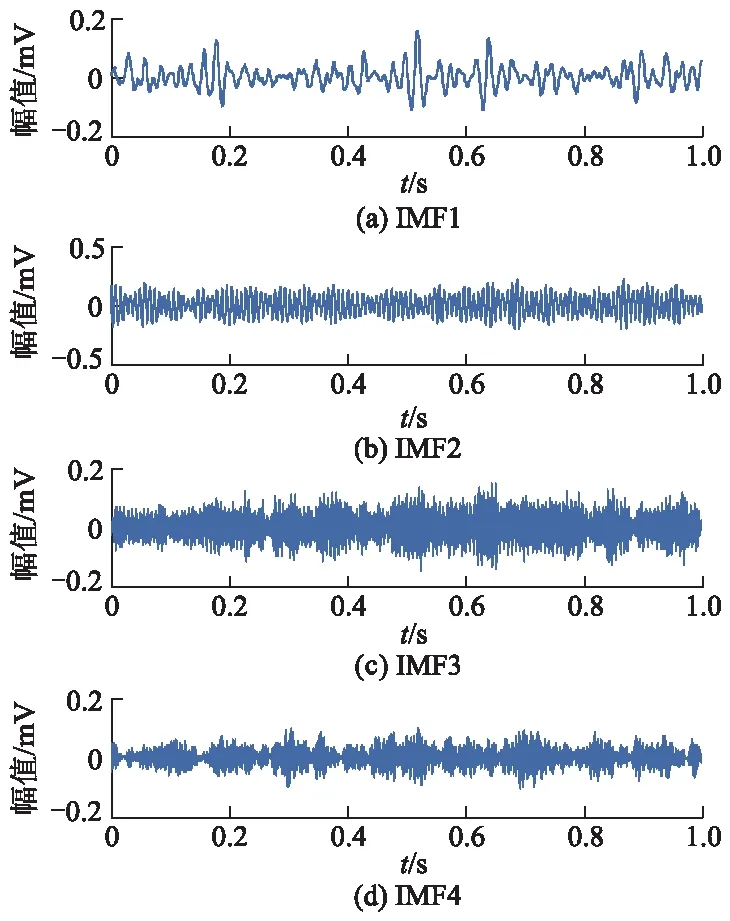
图8 不平横信号的VMD分解

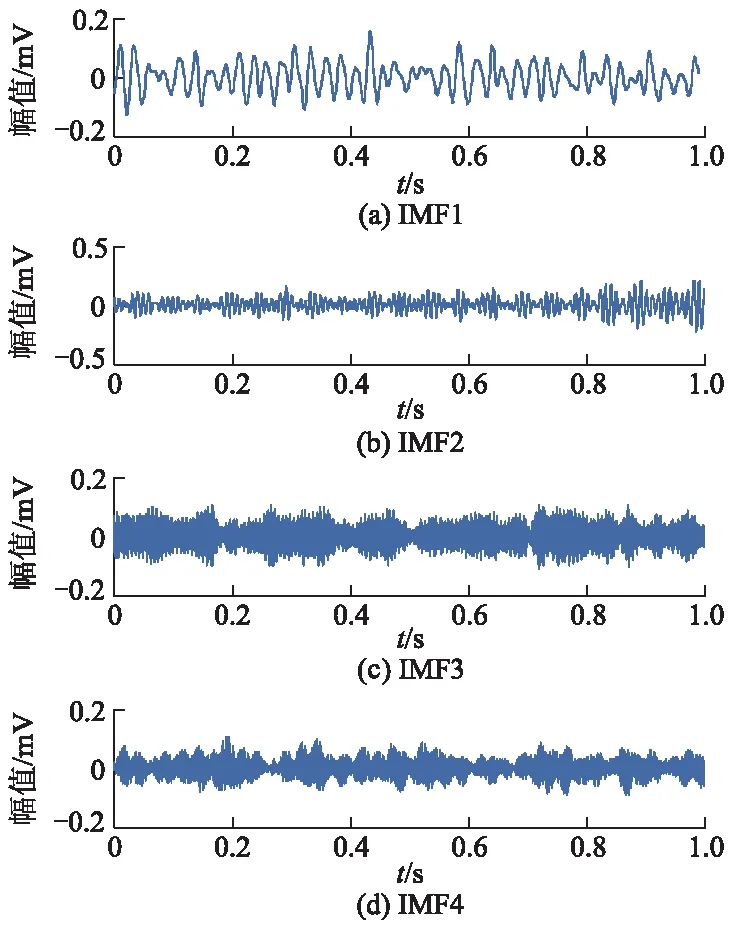
图9 松动信号的VMD分解

对不同工况下得到IMFs进行AR谱分析，得到不同工况信号分解后的各个IMF分量信号的功率谱，图10为4个分量IMF的VMD-AR谱对比图，图11为不同工况下的VMD-AR谱累加能量图.

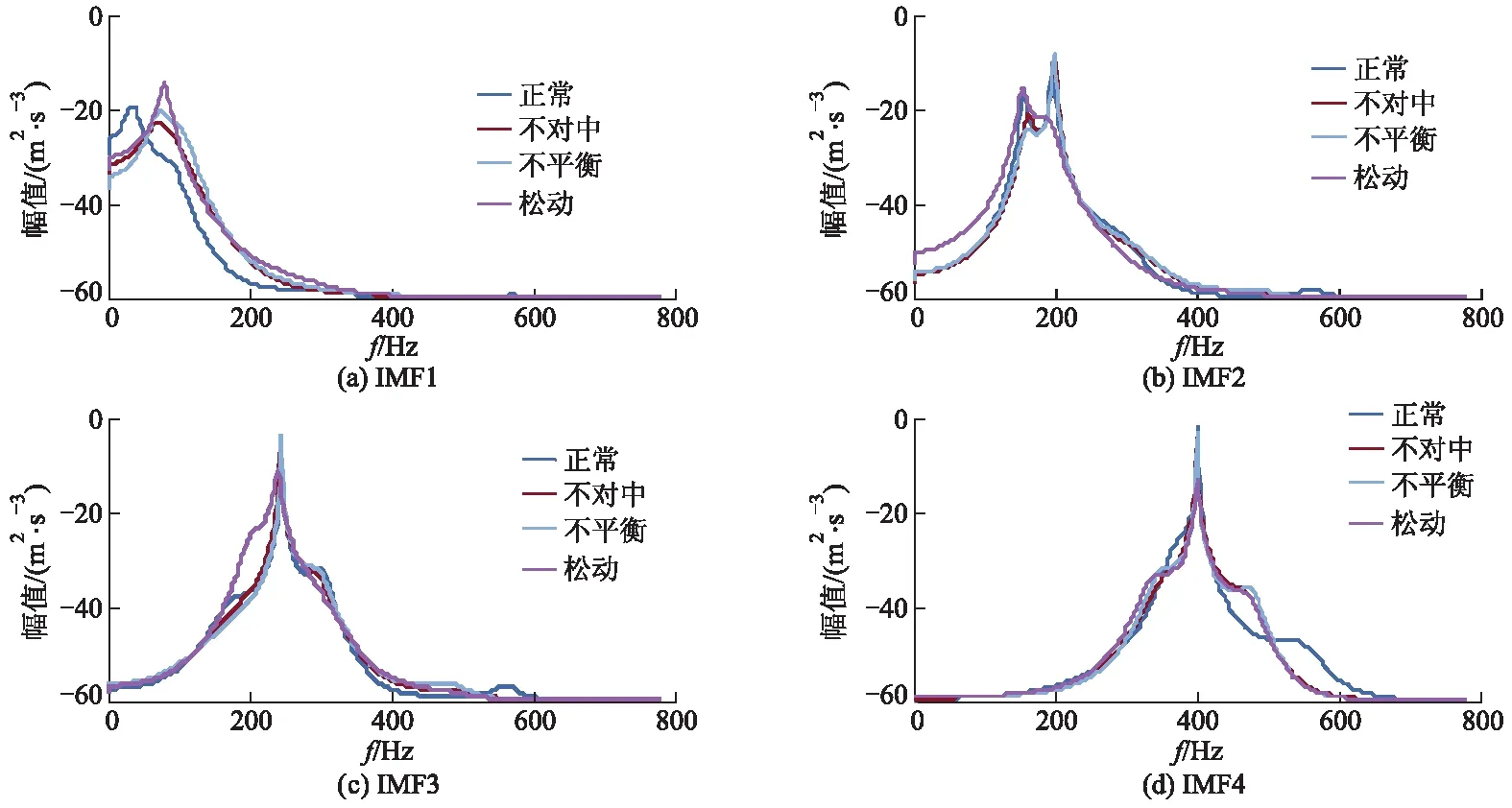
图10 不同故障的VMD-AR谱分析图

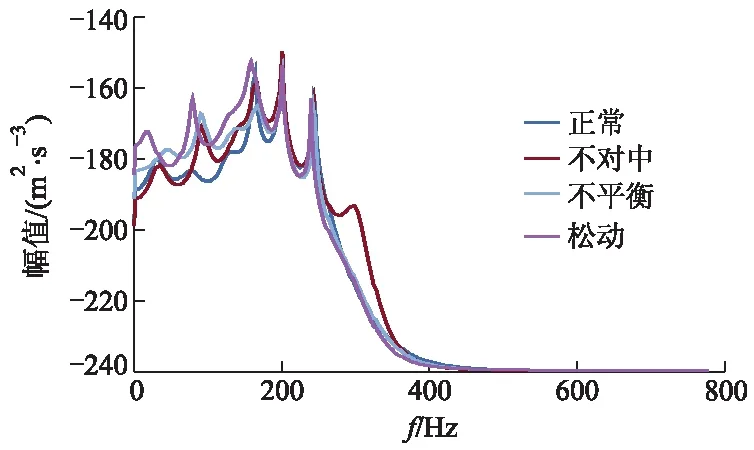
图11 VMD-AR谱累加能量图

由图观察，可见：

1) 设定多轴转子系统以转速2 500 r·min-1工作，通过对图10各个工况下的IMFs分量信号的功率幅值和图11中VMD-AR谱的累加功率幅值分析，可知4种工况的能量主要集中在600 Hz以内.

2) 从图10可见，能量由正常到不对中的特征频带有: IMF1分量范围为52～290 Hz，IMF2分量范围为160～200 Hz，IMF3分量范围为0～150 Hz，IMF4分量范围为260～360 Hz；能量由正常到不平衡的特征频带有:IMF1分量范围为50～290 Hz，IMF2分量范围为190～220 Hz，IMF3分量范围为0～160 Hz，IMF4分量范围为300～380 Hz，能量由正常到松动的特征频带有:IMF1分量范围为53～400 Hz，IMF2分量范围为0～176 Hz，IMF3分量范围为164～246 Hz，IMF4分量范围为260～370 Hz.

3) 从图11可见，能量由正常到不对中的特征频带有88～182 Hz；能量由正常到不平衡的特征频带有35～183 Hz；能量由正常到松动的特征频带有0～190 Hz.

4 结 论

1) 改进了VMD方法对于k值的人工经验选取，提出了瞬时频率均值法确定分解模式数k，有效地解决了分解模式数确定难题.

2) 建立AR时序模型，针对VMD分解信号得到的IMFs信号进行特征能量分析，并比对不同工况下的IMFs信号的AR谱能量，分析出不同故障形式下的特征频带.

3) 提出的VMD-AR谱故障特征提取方法以特征频带表征不同的故障形式，对多轴转子系统进行故障信号进行诊断，为多轴转子系统提供了一种故障信号诊断方法.