国产核心器件构建多通道模拟量采集系统的精度分析与设计
王 农,雷海军,袁 媛,于海祥,张明伟
(北京控制工程研究所,北京 100190)
0 引言
现代卫星驱动控制系统对模拟量的采集通道和采集精度的要求日益增高。多通道模拟量采集系统通常由模拟开关和模数转换器(ADC)等核心器件构成。目前,国内外关于多通道模拟量采集系统的设计与验证相关文献较多[1-9],但讨论的重点几乎全部集中在系统组成方面,而关于采集精度及其影响因素的系统论述几乎没有。多通道模拟量采集系统的采集精度通常由ADC输入端和参考端的模拟信号链决定,而该部分电路通常根据厂商提供的参考电路实现。由于缺乏对系统精度分析和核心器件选型的理论依据,经常出现根据实际应用修改电路参数后采集精度无法满足预期的问题。
鉴于上述背景,基于国产多通道模拟开关和开关电容ADC构建多通道模拟量采集系统,重点对系统采集精度及其影响因素进行分析,分别建立系统静态误差和动态误差的分析模型,并通过试验进行验证,为核心器件选型和国产化替代建立理论依据。
1 系统组成及原理

图1 多通道模拟采集系统图

图2 静态误差分析模型
基于国产核心器件构建的多通道模拟量采集系统如图1所示,包括通道切换模块、阻抗变换模块、滤波模块、AD转换模块和数字控制模块。通道切换模块由8片16通道模拟开关(MUX1-MUX8)组成,构成128个模拟量采集通道;阻抗变换模块由运算放大器(OP1-OP8)构成的电压跟随器实现,用于对模拟开关的输出信号进行隔离,消除模拟开关导通电阻和输入限流电阻对采集精度的影响;滤波模块由一阶RC电路构成抗混叠滤波器,其滤波电容同时作为电荷泵用于提供或吸收AD转换过程中产生的瞬态电流;AD转换模块由8通道开关电容ADC实现,完成从模拟量到数字量的转换;数字控制模块由FPGA和MCU实现,用于完成模拟开关通道切换和数据处理。该系统的基本工作原理与现有技术[7-9]相比并无本质区别,不再赘述。这里重点对采集系统的精度影响因素进行分析。
概括来讲,多通道模拟量采集系统的精度影响因素主要包括两个:由模拟信号链静态参数的非理想性引入的静态误差和由动态参数的非理想性引入的动态误差,下面分别详细论述。
2 静态误差影响因素分析
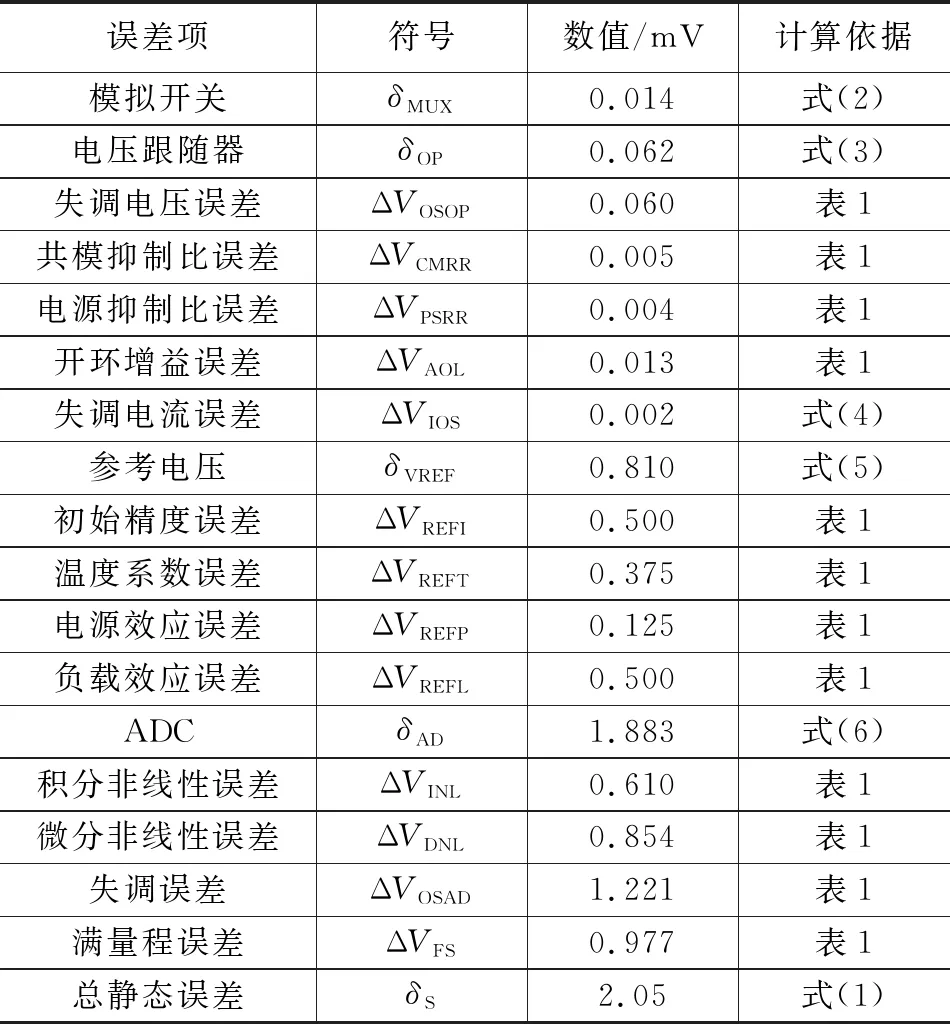
图2为图1所示系统中单个测量通道的静态误差分析模型。可见,系统静态误差主要来源于模拟开关、电压跟随器、参考电压和AD转换器。通常,认为上述误差项彼此独立且互不相关,因此系统静态误差δS应满足:
(1)
式中,δMUX、δOP、δVREF和δAD分别为模拟开关、电压跟随器、参考电压和AD转换器引入的静态误差,且均为等效到ADC输入端的电压值。下面分别对各误差项进行详述。
2.1 模拟开关引入的静态误差
如图2所示,假设输入信号VIN的输出阻抗足够小而运放的输入阻抗足够大,则模拟开关引入的静态误差δMUX主要由输入限流电阻RCL、导通电阻RON和导通漏电流ID决定,可表示为:
δMUX=ID(RCL+RON)
(2)
2.2 电压跟随器引入的静态误差
电压跟随器通常由运算放大器(简称运放)构成,其静态误差主要来源包括失调误差ΔVOSOP,共模抑制比、电源抑制比和开环增益引入的误差ΔVCMRR、ΔVPSRR和ΔVAOL,以及失调电流IOS引入的误差电压ΔVIOS。通常,认为上述误差项彼此独立且互不相关,则运放引入的静态误差δOP可表示为:
(3)
式中,各误差项均为等效到运放输入端的误差电压。其中,ΔVOSOP、ΔVCMRR、ΔVPSRR和ΔVAOL可根据运放数据手册相关数值计算得到。
图2中,若有(RCL+RON+RIP)=RFB,其中RCL和RON分别为模拟开关输入限流电阻和导通电阻;RIP为运放输入限流电阻;RFB为运放偏置电流补偿电阻,则运放正向和负向偏置电流IBP和IBN的影响可以忽略。又知偏置电流和失调电流IOS近似满足(IBP-IBN)=IOS,则运放失调电流引入的误差电压ΔVIOS可表示为:
ΔVIOS=IOS(RCL+RON+RIP)
(4)
2.3 参考电压引入的静态误差
图2中,参考电压VREF为AD转换器提供电压参考,其误差将直接传递到AD转换器的输出码值。参考电压引入的静态误差主要来源于初始精度误差ΔVREFI、温度系数误差ΔVREFT以及电源调整率和负载调整率引入的误差ΔVREFS和ΔVREFL。通常,上述误差项彼此独立且互不相关,则参考电压引入的静态误差δVREF可表示为:
(5)
式中,各误差项的具体数值可根据参考电压数据手册相关数据计算得到。
2.4 AD转换器引入的静态误差
若AD转换器输入端和参考端模拟信号链引入的误差可以忽略,则系统精度将取决于AD转换器自身误差。AD转换器的静态误差主要来源于积分非线性误差ΔVADINL、微分非线性误差ΔVADDNL、失调误差ΔVADOS和满量程误差ΔVADFS。若认为上述误差项彼此独立且互不相关,则AD转换器引入的静态误差δAD可写为:
(6)
式中,各误差项的具体数值可根据AD转换器数据手册相关数据进行计算。
3 动态误差影响因素分析
概括来讲,系统动态误差主要取决于ADC采样阶段输入信号的建立精度和转换阶段参考信号的建立精度。
3.1 输入信号的建立时间和建立精度
图3所示为模拟开关从切换通道后到ADC启动采样前的动态误差分析模型。可见,ADC输入信号的建立精度主要取决于前端模拟信号链的建立时间,主要影响因素包括:模拟开关的建立时间tMUX、电压跟随器的建立时间tOP和抗混叠滤波器的建立时间tFLT。通常,认为上述建立时间彼此独立且互不相关,因此输入信号的建立时间tSIG可表示为:
(7)
式(7)中,模拟开关的建立时间tMUX主要包括通道切换时间和寄生参数引起的延迟时间,即:
tMUX=tMUXSW+tMUXRC
(8)
式中,tMUXSW为通道切换时间;tMUXRC为导通电容CON、导通电阻RON和限流电阻RCL引入的延迟时间,可表示为:
tMUXRC=KNBIT(RCL+RON)CON
(9)
式中,KNBIT为一阶RC电路达到N位建立精度的时间常数系数,可表示为:
KNBIT=ln(2N)
(10)
式(7)中,电压跟随器的建立时间可根据运放的压摆率SROP进行估算:
(11)
抗混叠滤波器的建立时间tFLT可表示为:
tFLT=KNBITRFLTCFLT
(12)
式中,RFLT和CFLT分别为滤波电阻和滤波电容。
要保证ADC启动采样前输入信号具有N位的建立精度,模拟开关切换通道后的延迟时间tD应满足:
tD≥tSIG
(13)
此外,如图3所示,ADC开始采样瞬间,即内部开关SWT闭合瞬间,滤波电容CFLT和跟随器同时对采样保持电容CTH充电,ADC输入端电压出现反冲。要保证采样结束时输入信号再次达到N位建立精度,要求抗混叠滤波器的时间常数τFLT与ADC的采样时间tACQ满足如下关系式[10]:
(14)

图3 动态误差分析模型
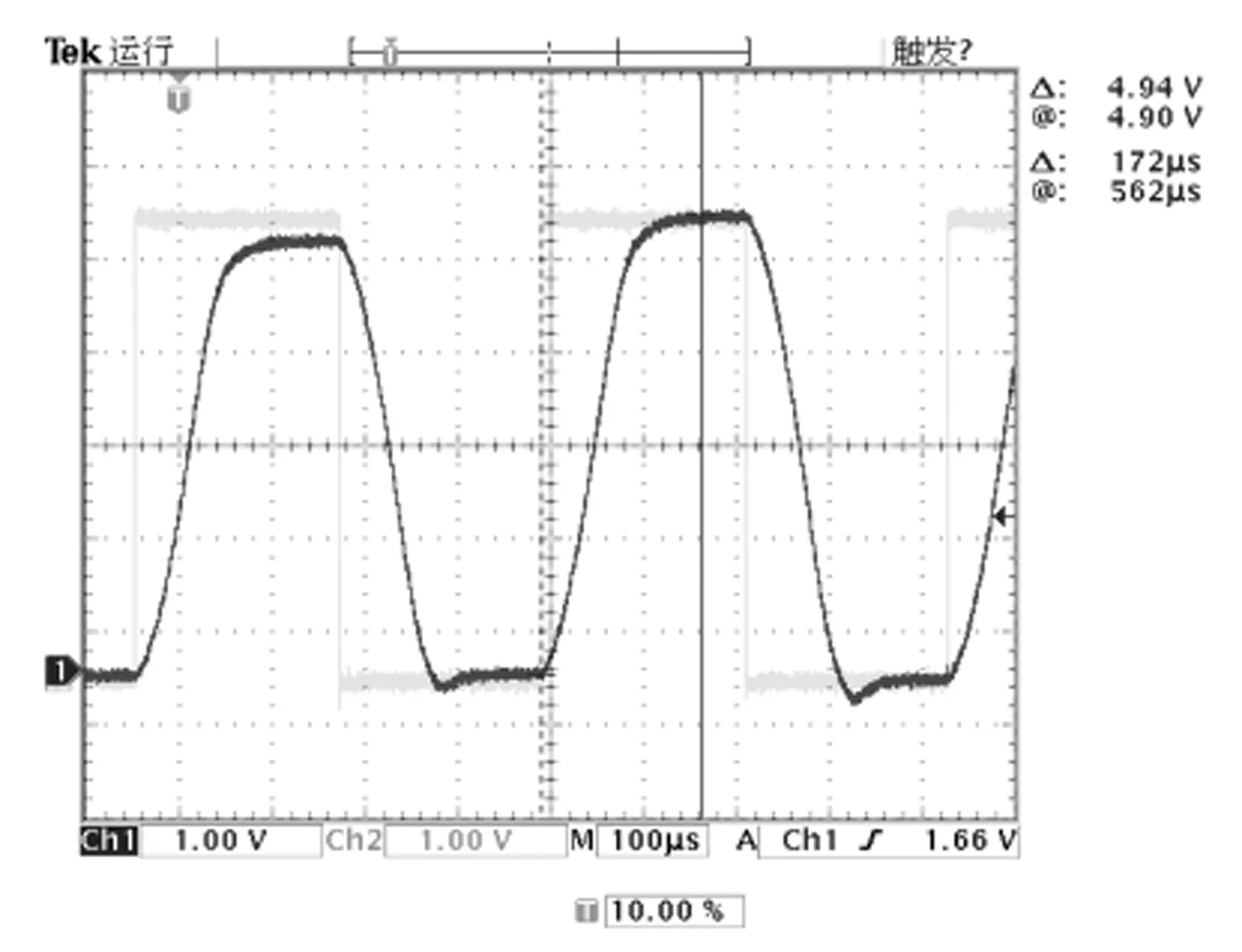
式(14)推导过程中,假设跟随器的-3 dB带宽大于抗混叠滤波器的4倍,且滤波电容CFLT与采样保持电容CTH之间的关系满足10CTH 然而,在宇航产品设计中,受元器件选用限制,上述假设经常难以满足。在此情况下,提出一个经验法则,即在满足系统采样速率和可靠性设计的前提下,滤波电容CFLT的取值应尽可能大,但要保证前级跟随器具有足够的相位裕度。 与ADC输入端负载特性类似,参考端负载特性也呈动态阻抗。ADC转换阶段,内部切换开关以转换时钟频率对各权值电容进行切换,因而需要参考电压对各权值电容进行快速充放电以保证建立精度。为了提高参考电压对瞬态电流的驱动和吸收能力,通常在其输出端设置电荷缓冲电容,用于在ADC转换阶段迅速提供或吸收参考端瞬态电流。要保证ADC转换阶段参考信号的建立精度达到N位,缓冲电容CREF应满足如下关系式[10]: (15) 式中,N为ADC的分辨率;IREF为参考端平均电流;tCON为ADC转换时间;VREF为参考电压。 图1所示系统选用的核心器件及相关参数[11-12]如表1所示。 表1 系统选用的核心器件及相关参数 除参考电压VREF的初始精度(0.5 mV)为实际校准值外,表中数据均来源于器件手册典型值。此外,图1中RCL=RIP=ROP=1 k是为兼顾系统可靠性增加的必需器件;抗混叠滤波器参数为RFLT=200 Ω,CFLT=100 nF;参考端缓冲电容CREF=4.7 μF;AD584设计为5 V输出,最大瞬态电流约为5 mA;模拟开关和运放共用12 V供电(VDD= +12 V,VSS=-12 V),最大变化量为0.5 V;环境温度最大变化量约为5℃。需要说明的是,该设计将抗混叠滤波器的时间常数设计为较大值(20 μs),是因为前级跟随器的单位增益带宽较小,典型值0.6 MHz,不满足式(14)的假设条件。因此,只能通过增大滤波电容CFLT以降低采样期间ADC输入端的反冲电压来保证采样期间输入信号的建立精度。 对表1所示相关数据进行单位统一和数值换算后,可得系统静态误差如表2所示。 表2 系统静态误差估算 可见,系统静态误差估算值约为2.05 mV,主要来自ADC自身失调误差(1.221 mV)。上述结果表明,该系统中模拟开关、跟随器、参考电压及其外围电路的选型和设计合理,引入的静态误差基本可以忽略。 根据表1所示相关数据,可得ADC输入最坏情况下(相邻通道间的最大压差为5 V)的建立时间约为167.19 μs,如表3所示。因此,根据式(13),将模拟开关切换通道后的延迟时间设计为256 μs,理论上可以保证ADC开始采样时输入信号的建立精度达到12位分辨率(1.221 mV)。 表3 建立时间估算(建立精度为12位分辨率) 由式(15)可知,缓冲电容CREF的最小值应为3.33 μF,实际设计值为4.7 μF,理论上可以保证ADC参考信号的建立精度达到12位分辨率(1.221 mV)。 随机选取模拟量采集系统的2个通道进行测试,结果如表4所示。 表4 随机选取两个通道的实测结果 试验过程中,与被测通道相邻的两个通道均设为0 V以模拟最坏工况。表中各设置值(被测信号)由6位半直流电压发生器ADCMT 6166的10 V量程输出,各设置值由7位半万用表Keysight 34470A进行监测,实测各设置值的绝对精度优于0.2 mV,小于12位ADC分辨率(1.221 mV)的1/3,因此表中数据未考虑该误差的影响。表中,Ch1采集值和Ch33采集值为采集系统的第1和第33通道的实际测量值;Ch1误差和Ch33误差为各实测值相对于设置值的绝对误差。 表4表明,被测通道满量程内的最大误差绝对值约为1.60 mV(Ch1设置值为2 000 mV时,采集值为1998.40 mV),该结果略小于表2所示的系统总静态误差估算值2.05 mV,说明抗混叠滤波器参数设计合理,且ADC采样和转换期间未引入明显的动态误差,这与3.1和3.2所述的预期结果相符。实测最大误差值1.60 mV小于理论估算值2.05 mV,原因很可能是估算时采用的数据均为器件参数典型值,而系统实际使用的器件参数优于手册典型值。 图4为模拟开关切换通道后输入信号的波形图。其中,Ch1为模拟开关地址A0信号,Ch2为ADC输入端信号(抗混叠滤波器输出端信号)。可见,模拟开关切换通道后,输入信号由0 V上升到5 V的建立时间约为172 μs,与表3所示的理论估算值167.19 μs非常吻合。该结果同时表明将通道切换后的延迟时间设为256 μs满足理论要求值并具有足够的设计裕量,从而保证系统在宽温度范围或其它恶劣环境中工作时具有足够的可靠性。 图4 模拟开关切换通道后输入信号的波形图 最后,需要说明的是,理论上可以采用软件校准的方法提高系统测量精度,但对于具有上百个通道的测量系统来讲该方法并不实用。从表2可以看出,当ADC器件确定后,进一步提高系统测量精度的方法是选用初始精度更高、而温度系数和负载调整率更低的参考电压。 针对核心器件国产化替代过程中多通道模拟量采集系统的精度设计缺乏理论依据的问题,对基于多通道模拟开关和开关电容ADC构建的多通道模拟量采集系统的精度影响因素进行了系统研究,分别建立了系统静态误差和动态误差的分析模型,为关键器件选型建立了理论依据。研究结果表明:系统精度影响因素包括静态误差和动态误差。其中,静态误差主要由ADC输入端和参考端的模拟信号链决定,主要来源于模拟开关、跟随器、参考电压和ADC自身静态参数的非理想性;动态误差主要由ADC采样阶段输入信号的建立精度和转换阶段参考信号的建立精度决定。上述结论分别通过了理论和试验验证,对设计或改进多通道模拟量采集系统的测量精度具有普遍指导意义。3.2 参考信号的建立时间和建立精度
4 实验结果与分析
4.1 系统设计

4.2 静态误差估算
4.3 动态误差估算

4.4 试验验证

5 结束语

