基于改进灰色模型的模拟电路故障预测研究
王 昊,李旷代,张晓光,李春华,沈海阔,张 朔
(1.北京交通大学 机械与电子控制工程学院,北京 100044;2.北京宇航系统工程研究所,北京 100044;3.中国船舶重工集团有限公司第七一五研究所,杭州 310023)
0 引言
飞行器信息处理设备是导弹制导系统的重要组成。在实际工况中,信息处理设备主要是对弹上采集系统采集的制导图像进行信息处理,并将图像处理结果同时发送给飞行控制组合和人机交互界面进行显示。信息处理设备供电电源主要为息处理机各功能模块提供安全电源,是一个典型的模拟电路。随着军用电子系统的复杂度和集成度的加速增长,我国对军用装备的可靠性和维修性的认知发生了很大的改变,由传统的事后维修逐渐向视情维修转变。在武器装备系统全生命周期费用中,使用和保障费用高达72%,与研发使用费用相比,维修保障费用在技术上更具有可压缩性[1]。视情维修作为一种降低维修保障费用的重要技术手段主要是通过故障预测来实现。在故障预测常用的方法中灰色理论以其小样本、无规律样本分布和较高预测精度被广泛使用[2]。
1 故障预测特征参数选取
故障预测特征参数表征了被预测系统的实时运行状况,应随着系统的退化发生单调变化,而且在一定变化范围内能有效区分。
信息处理设备电源模块主要负责整个设备的电源供应,主要涉及DC/DC模拟电路,BUCK电路可实现降压功能,是DC/DC电路中最基本的电路之一。以BUCK电路为例,在MATLAB仿真平台下,利用Simulink建立电路模型。设定电路不同的工作条件及元器件参数,并进行电路仿真和状态信号的采集,最终确定模拟电路采用的特征参数。
1.1 BUCK电路Simulink仿真
BUCK电路的原理如图1所示。

图1 BUCK电路原理图
其中:E为输入电压,Sw为MOSFET开关,Ts为周期性的矩形波,为MOSFET开关提供周期的通断状态。当处于高电平时,开关管处于导通状态,电感L被充磁,流经L的电流线性增加,同时给电容C充电,给负载R提供能量。当处于低电平时,开关管处于断开状态,L通过二极管D续流放电,输出电压靠滤波电容放电以及减小的电感电流维持。
根据BUCK电路原理图,利用simpowersystems中的模块建立仿真模型,如图2所示。其中IGBT/Diode模块模拟MOSFET开关,Pulse Generator模块产生脉冲驱动开关管,Simout模块和Scope模块方便读取纹波电压值,输出电压读取有效值。
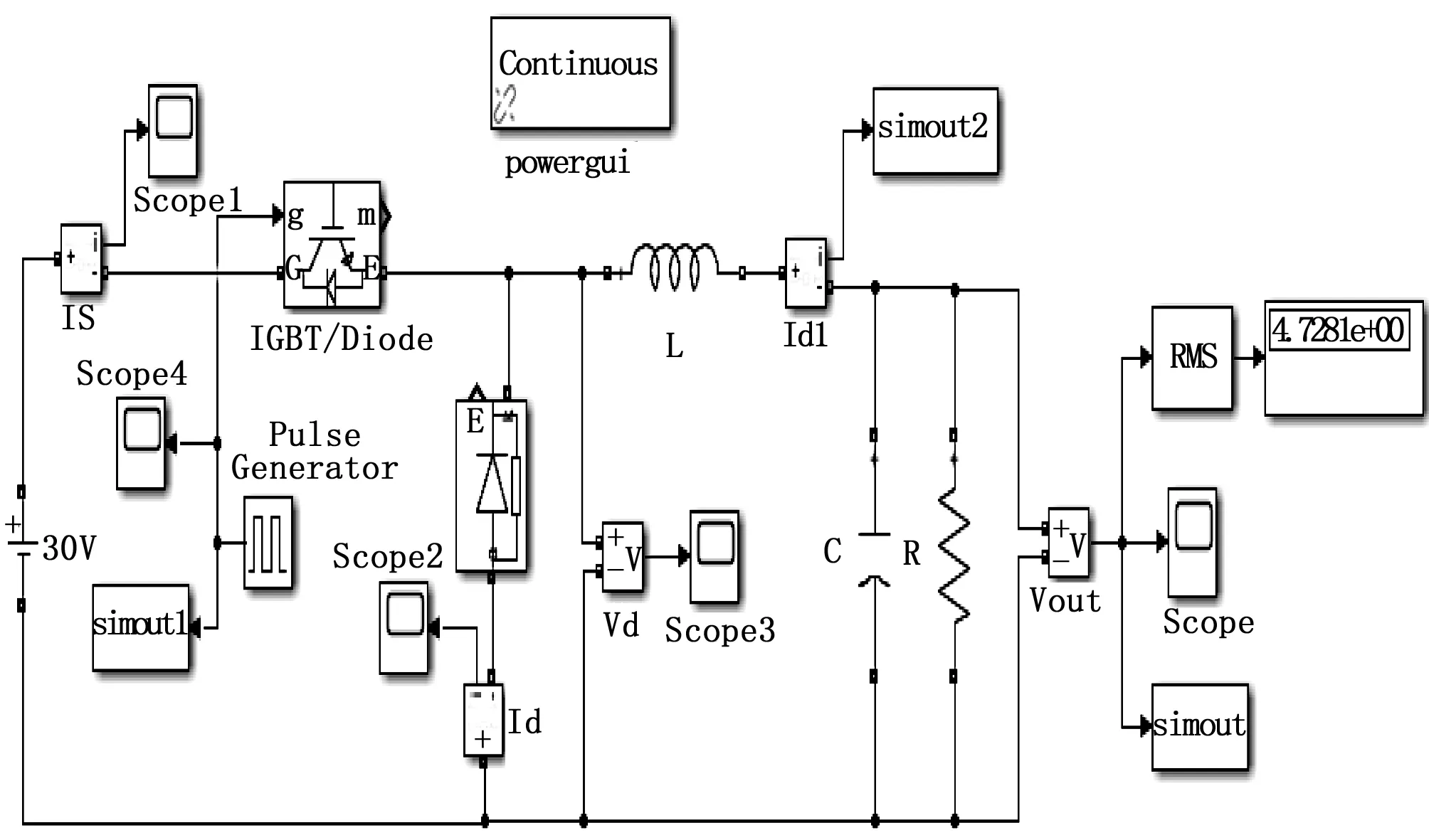
图2 BUCK电路Simulink仿真
1.2 电路元器件初始值计算
设置初始参数,输入电压20 V,输出电压5 V,负载电阻10 Ω,工作频率10 kHz,要求纹波电压值不超过输出电压的0.5%。BUCK电路Simulink仿真模型纹波电压的误差应控制在10%以内,认为建立的仿真为有效模型。
根据以下公式计算仿真电路电容值C0和电感值L0。
(1)
其中:D,Ts分别为占空比,脉冲周期;V0,Vd,I0分别为输出电压、输入电压、负载电流。
由式(1)可以得出在纹波电压小于0.025 V条件下,占空比为0.25,电容初估值为C0=500 μF,电感的初估值L0=0.375 mH。
当占空比为0.25(输入电压20 V,输出电压5 V),工作频率fs=10 kHz,电容C0=500 μF,电感L0=0.375 mH条件下,计算的理论纹波电压值为0.025 V,通过示波器读取的BUCK电路Simulink仿真模型的纹波电压值为0.026 7 V,理论误差为6.8%控制在10%以内,由公式(1)中计算的电感电流波动的理论值为1 A与读取的图像的波动值1 A相吻合,由此判断此BUCK电路Simulink仿真模型有效。
1.3 模拟电路退化过程
仿真模型建立后,需要模拟电路各元器件的退化过程,以期找到能够表征BUCK电路退化的特征参数。初选输出电压和输出电压纹波值为电路的特征参数。查阅大量文献,研究电路中各元器件的理论退化模型如下:
电解电容工作时间越长,其电解液的损耗也就越多[3], J.R.Celaya等人通过试验研究建立了电解电容的退化模型—电容减小百分比[4],见式(2):
△C(t)=eat-β
(2)
其中:t为电容使用时间,α、β为常数。规定当电容相对初始值降低20%时视为失效[5]。
电感线圈的温度会随着工作的时间增加导致电感储能容量降低[6]。具体退化模型见式(3):
L(t)=L0-at
(3)
其中:t为电感的工作时间,a为模型的退化参数,L0为电感的初始值。经过国内外多位研究学者的试验,证明当L的值较初始值降低了20%时,则表明其已失效[7]。
由BUCK电路电容初始值,根据电容失效条件设计输出电压V0与纹波电压△V0随电容C变化的单因子变量实验,MOSFET管内阻设为0.02 Ω,二极管导通内阻设为0.02 Ω,电感L0=0.375 mH。由式(2)认为当电容C0=500 μF纹波电压值超出输出电压的0.5%,电路发生失效。规定当电容相对初始值降低20%时视为失效,在490~610 μF范围每10 μF设定一个数据点,具体数据见表1。
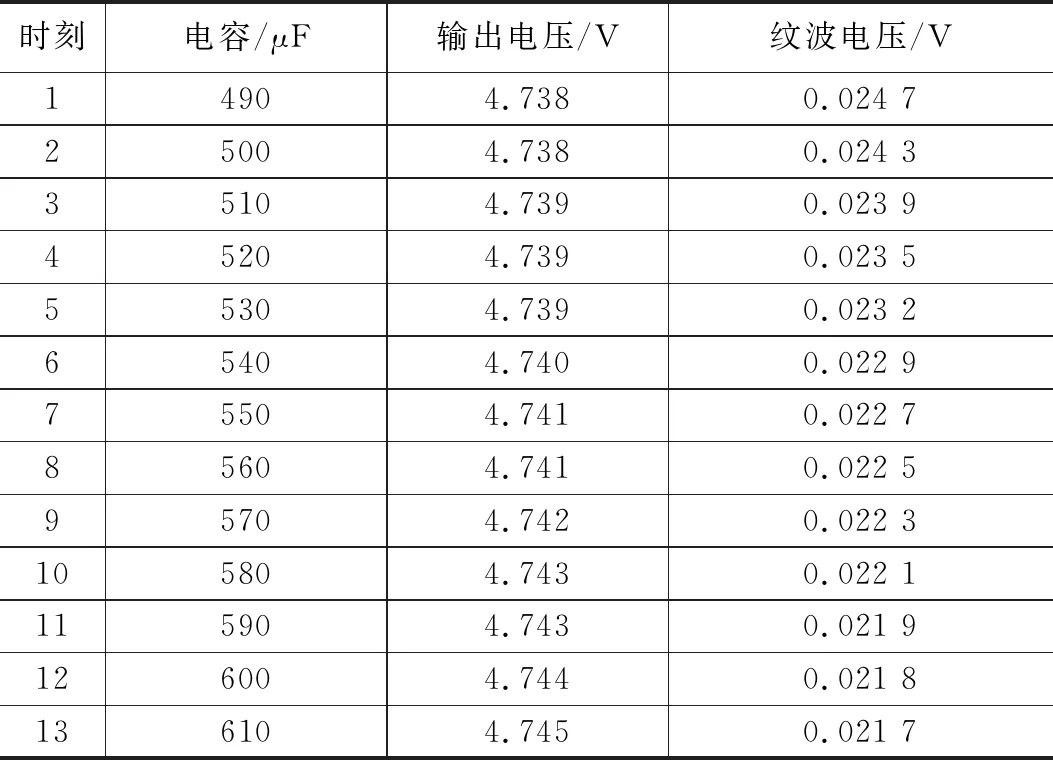
表1 特征参数与电容变化
采用最小二乘法分别对输出电压纹波电压用基本函数进行拟合,拟合结果见表2。

表2 随电容变化拟合精度
R2是拟合程度的指标,它的数值大小可以反映趋势线的估计值与对应的实际数据之间的拟合程度,拟合程度越高,趋势线的可靠性就越高。R2取值范围在0~1之间,当趋势线R2等于 1 或接近 1 时,其可靠性最高,反之则可靠性较低。从表2可以知道,随电容变化,输出电压拟合结果中线性变化的R2值最接近1为0.972,可认为输出电压呈线性变化趋势,纹波电压拟合结果中指数变化的R2值最接近1为0.979。可认为纹波电压呈指数变化趋势。
由BUCK电路电感初始值,根据电感失效条件设计输出电压V0与纹波电压△V0随电容C变化的单因子变量实验,MOSFET管内阻设为0.02 Ω,二极管导通内阻设为0.02 Ω,电容C0=500 μF。由式(2)认为当电容L0=0.375 mH纹波电压值超出输出电压的0.5%,电路发生失效。当L的值较初始值降低了20%时,则表明其已失效,在0.375~0.460范围每0.005 mH设定一个数据点,具体数据如表3所示。

表3 特征参数与电感变化
采用最小二乘法分别对输出电压纹波电压拟合,结果见表4。

表4 随电感变化拟合精度
从表4可以知道,随电感变化,随电容变化,输出电压拟合结果中幂函数趋势变化的R2值最接近1为0.976,可认为输出电压呈幂函数趋势变化,纹波电压拟合结果中线性变化的R2值最接近1为0.979。可认为纹波电压呈线性变化趋势。
综合以上两组单因子仿真实验结果,参照式(2)电容退化模型和式(3)电感退化模型,纹波电压更能反映BUCK电路退化趋势,故选取纹波电压作为故障预测的特征参数进行研究。
2 故障预测模型
飞行器信息处理设备供电系统的故障预测是一个典型的模拟电路故障预测,常用的故障预测方法主要有基于内建“故障标尺”的故障预测、基于失效物理模型的故障预测和基于数据驱动的故障预测[8]。分析信息处理设备供电系统的结构特点可知其中既包括已知的白色信息,也包括未知的黑色信息。基于数据驱动的故障预测中的灰色理论以其小样本、无规律样本分布和较高预测精度在复杂系统中被广泛使用。所以此处选用灰色理论作为信息处理设备供电系统的故障预测模型。
自邓聚龙教授提出灰色模型系统理论后,很多专家学者对灰色模型进行了深入的探讨,结合自己研究领域提出相应的学术观点,成功的解决了大量生产与科研中的实际问题。GM(1,N)模型是最常用的预测模型,应用也相对比较成熟,其中N表示灰色预测模型中变量的个数[9]。
2.1 GM(1,1)模型
灰色模型对原始数据的随机性表现的比较敏感,即原始数据的粗劣程度越大,灰色模型的预测精度越低[10]。邓聚龙教授指出:原始数据矩阵的构造对于灰色模型的建立起着至关重要的作用,由于原始数据的随机性,会导致矩阵中某行(或某列)的数据之间产生较大差距,最终造成解的漂移。GM(1,1)模型为了解决该问题,要对原始数据序列进行数据预处理以减少序列的随机性,增加序列的规律性。
GM(1,1)模型建模过程如下:
1)原始序列累加:
GM(1,1)模型模型一对原始序列累加生成一次,减少原始数据的随机性,增加模型的预测精度。设有原始序列:
X(0)=(X(0)(t1),X(0)(t2),...,X(0)(tn))
(4)
则一阶累加序列为:
X(1)=(X(1)(t1),X(1)(t2),...,X(1)(tn))
(5)
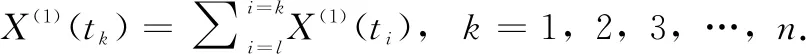
2)一阶灰色模型建立:
(6)
(7)
X(0)(K+1)+aZ(1)(k+1)=u
(8)
3)最小二乘法求a,u的估计值:
(a,u)T=B-1Y=(BTB)-1BTY
(9)
4)求解预测模型:
(10)
累减生成与累加生成互为逆运算,一般用来获取序列中相邻数据的差值。
(11)
(12)
有时候数据序列会出现明显的异常点,应删除送些异常点增加序列的平滑性,但是这样会使该序列出现空缺点。均值生成是填补该序列空缺的常用方法,称Z(0)(tk+1)=0.5X(0)(tk+1)为原始序列紧邻均值生成值。
2.2 改进的GM(1,1)模型
GM(1,1)模型是灰色理论中比较成熟的模型,具有建模简单、准确的优点, 通过对建模过程进行分析,影响模型精度的因素主要有两方面:1)数据的预处理;2)训练模型所用数据的维数。原始数据波动性较大会导致预测模型精度降低,此外,装备的性能退化通常被认为是一个累积过程,历史信息包含了装备的性能退化信息,从时间尺度上看,距装备当前状态时间越长的历史信息对故障预测建模的贡献率越低,因此,训练模型的数据维数和建模贡献率会影响灰色模型精度.改进的GM(1,1)模型建模过程如下:
1)原始数据平滑预处理:为了减少原始数据的随机性和粗大误差,增加灰色模型的预测精度,在训练模型之前需要对训练数据进行平滑预处理。改进模型中,选用了4种基本函数对原始数据进行平滑处理,接下来以对数函数y=ln(x+1)为例介绍处理过程:
设原始数据为X(0)=(X(0)(t1),X(0)(t2),...,X(0)(tn)
数据平滑处理后的序列为:
Y(0)=ln(X(0)+1)
Y(0)=(Y(0)(t1),Y(0)(t2),...,Y(0)(tn))
2)处理后数据一阶线性累加:同式(5),将原始数据序列编程平滑预处理后的新数据Y(0)。

Y(0)=(Y(0)(t1),Y(0)(t2),...,Y(0)(tm0))
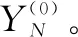
4)建立一阶灰色模型同式(6)~(8)。
5)最小二乘法求解模型参数同式(9)。
6)求解预测模型同式(10)~(11)。
求得序列Y(1)后,预测序列X(1)=eY(1)-1。
3 实验结果与分析
理想情况下 DC/DC电路的主要性能参数是规律变化或恒定不变的,但由于电路中元器件的性能退化和工作条件的变化,导致电路性能参数在电路由正常到故障过程中发生不同程度的变化,并且包含着一定的电路性能退化信息。
对飞行器信息处理设备的电源模块等时间间隔测量了20组纹波电压值,如表5所示。前10组数据用于训练故障预测模型,后10组数据用于检验模型精度。改进的模型用Matlab编程用于输出预测数据。
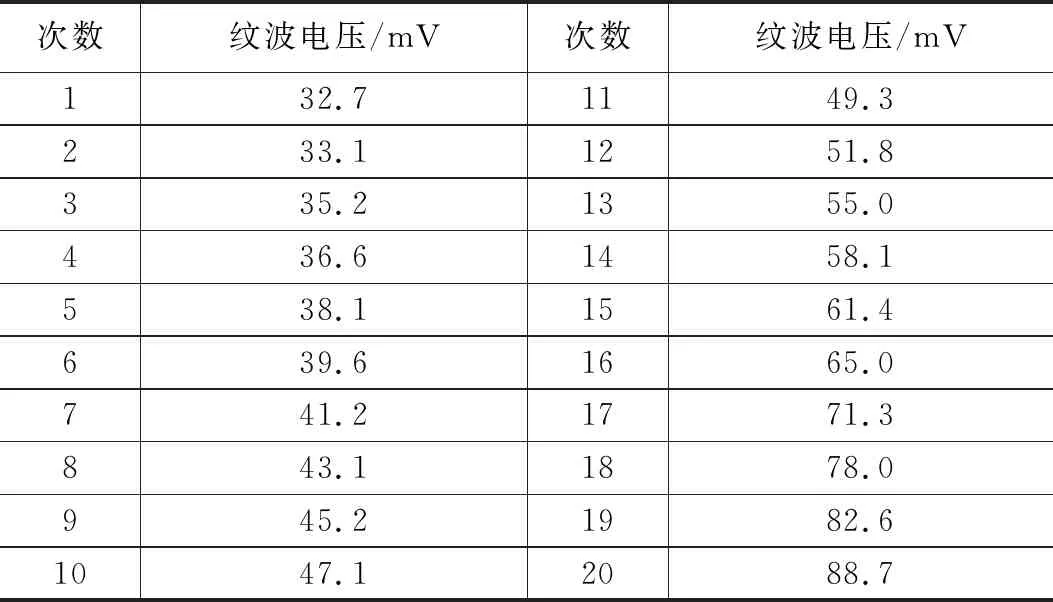
表5 信息处理设备纹波电压值
3.1 数据平滑预处理对比实验
前10组数据应用于GM(1,1)模型预测,数据分别采用y=ln(x+1),y=ex-1,y=x2,y=1/x四种基本函数进行平滑预处理,求取各自平均相对残差如表6所示,预测的10组数据绘制曲线图如图3所示。

表6 预处理数据预测精度
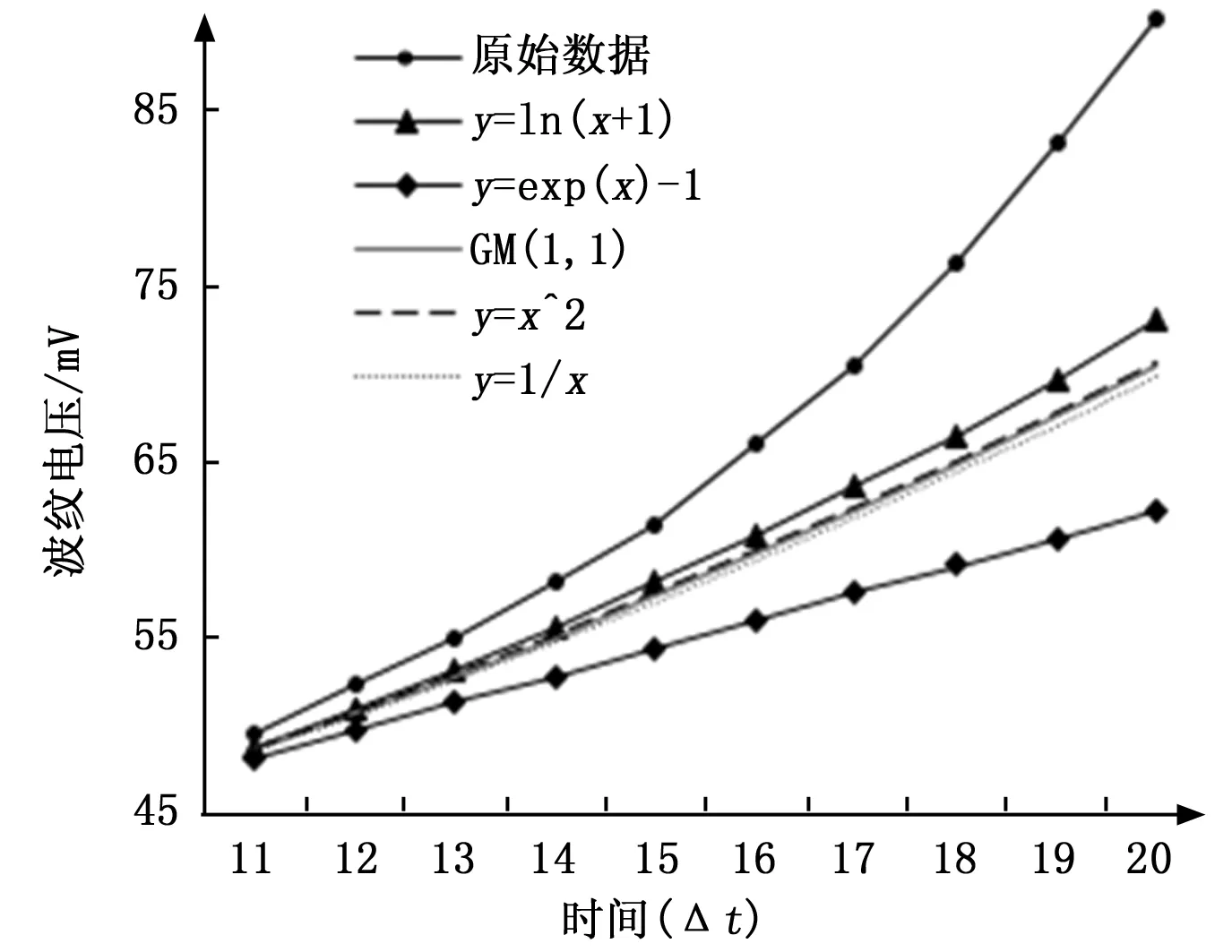
图3 数据平滑预处理对比
从图3中可以看出,在几种常用的基本函数种,经y=ln(x+1)预处理后的得到的预测数据曲线相对于GM(1,1)的出的预测数据曲线更接近于原始数据。从表6中也可以看出,经y=ln(x+1)预处理后的平均相对残差为8.26%相对于未处理的数据的9.65%有一定程度的提高。
3.2 训练数据降维对比实验
将用于训练模型的10维数据通过Matlab编程采用GM(1,1)模型进行降维处理,记录每组数据的平均相对残差绘制预测维数与平均相对残差曲线如图4所示。
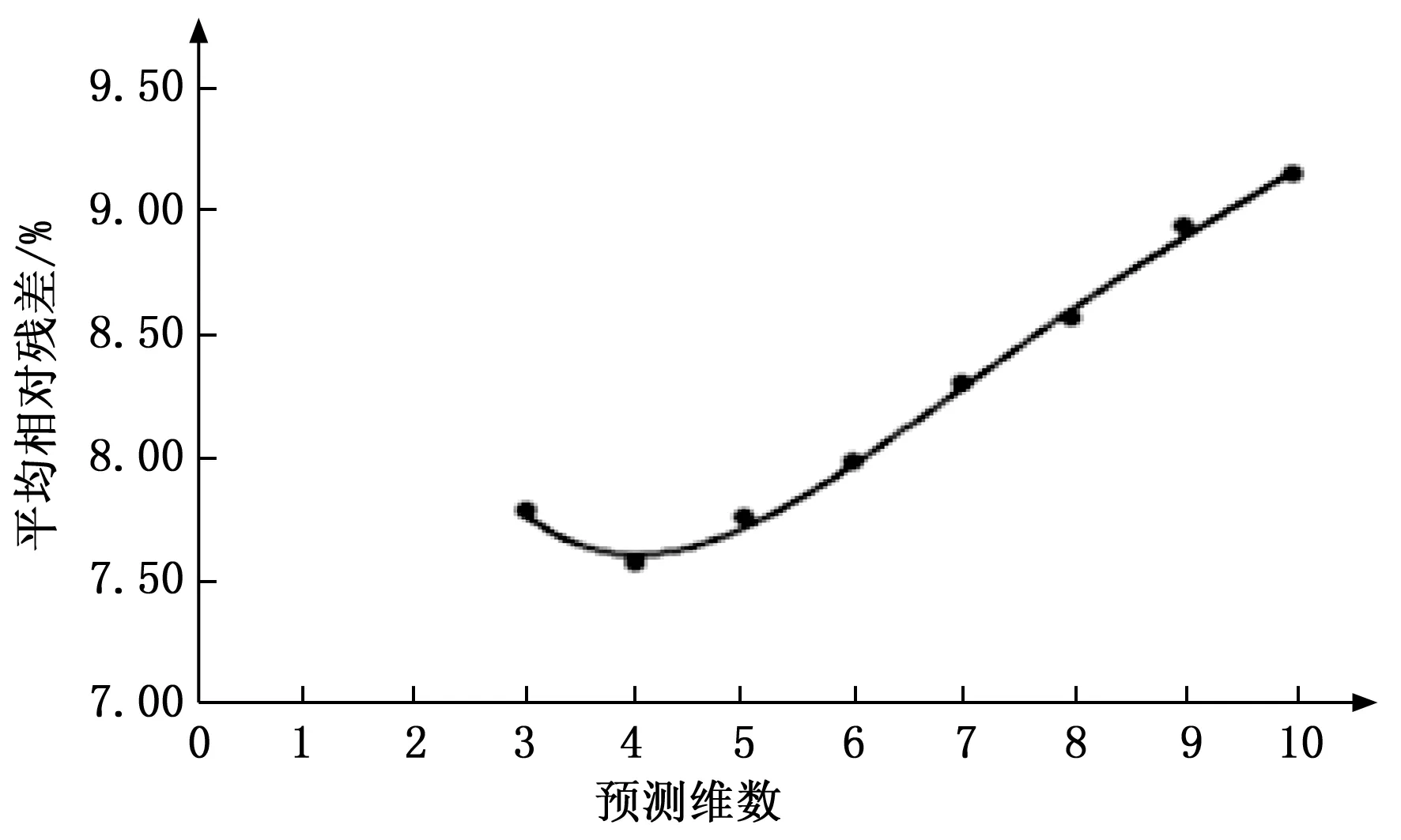
图4 训练数据维数与平均相对残差关系曲线
从图4中可以看出,当训练数据维数降到4维的时候平均相对残差达到最小值为7.57%预测模型的精度也最高。
综合以上两组实验结果,选用y=ln(x+1)做平滑预处理,训练数据的维数选用4维,更改Matlab程序,应用改进的具有适应度的数据平滑预处理灰色模型,并对比GM(1,1)模型,新陈代谢模型,绘制曲线图如图5所示。
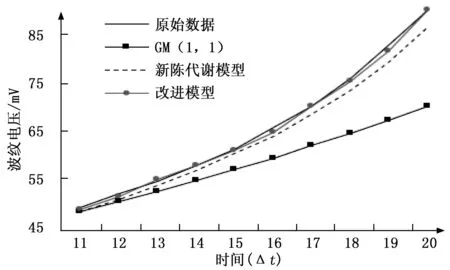
图5 改进模型对比
从图5中可以看出,提出的具有适应度的数据平滑预处理灰色模型的预测曲线相较于GM(1,1)模型和新陈代谢模型更接近原始数据曲线。改进后的模型平均相对残差为0.63%,相比于GM(1,1)模型的9.65%,新陈代谢模型的2.43%预测模型精度都要高。
4 结束语
本文以典型的BUCK降压电路为例研究模拟电路故障预测特征参数,通过Simulink仿真模拟电容电感退化过程,设计单因子变量实验确定纹波电压作为模拟电路故障特征参数。研究了灰色模型建模过程,从数据的预处理和训练数据维数入手改进得到了一种具有适应度的数据平滑预处理灰色模型。结合飞行器信息处理设备电源模块设计了数据预处理对比实验和训练数据降维对比实验,结合两组实验结果验证了改进模型的有效性和正确性。

