两级物流网络车辆路径问题研究综述

李红启 陈鋆 赵佳敏

摘 要：城市物流和多式联运等往往表现为多级物流网络模式。在多级物流网络上综合运用多种类型的、载运能力不同的车辆，可节约物流成本。在两级物流网络车辆调度运用过程中，货物需要在不同层级的车辆之间进行中转，两个不同层级的车辆路径方案之间需互动协同。由于其实践参考价值和建模求解的复杂性，两级物流网络车辆路径问题（2E-RP问题）相关研究成果在近年来不断涌现。文章梳理总结包括2E-VRP问题、2E-LRP问题、TTRP问题和VRPCD问题等在内的2E-RP问题的研究进展;基于2E-RP问题所对应的行业实践背景，为拓展2E-RP问题数学建模思路，提出促使两个层级车辆路径互动的新的驱动因素，即时效和运力匹配;指出后续研究2E-RP问题时可在建模方面的关注点。

关 键 词：两级物流网络;车辆路径问题;2E-VRP问题;2E-LRP问题;TTRP问题;VRPCD问题

中图分类号：F252.1;U116.2 文献标识码：A 文章编号：2096-7934（2020）09-0088-13

一、引言

由Dantzig and Ramser 于20世纪50年代末提出车辆路径问题（VRP问题）[1]以来的半个多世纪，针对VRP问题的研究成果很多（较新研究综述可参考Baldacci et al.（2007）[2]和Laporte（2009）[3]的相关研究）。相比于VRP问题，两级物流网络车辆路径问题（the two-echelon routing problem，本文简写为2E-RP问题）涉及两个不同层级上车辆路径方案之间的协同，该类问题的建模和求解难度更大。迄今多数研究工作均将2E-RP问题的研究背景定位于城市物流领域：由于越来越多的城市出台法规限制大型货车进入中心城区，待配送货物需要在不同类型车辆之间进行中转，从而衍生出多层级的物流网络形态。在学术界提出的两级物流网络上的车辆路径优化相关问题[4-5]中，在城市周边拟定若干中转站，货物在中转站进行中转等作业后，由小型车辆开展市内配送。

本文首先分析2E-RP问题所对应的行业实践背景;其次，梳理总结包括2E-VRP问题（the two-echelon vehicle routing problem）、2E-LRP问题（the two-echelon location routing problem）、TTRP问题（the truck and trailer routing problem）和VRPCD问题（the vehicle routing problem with cross-docking）等在内的与2E-RP问题相关的研究进展。为较为客观地审视2E-RP问题领域的研究脉络，本文重点关注发表于2016年之前的相关研究成果;发表于2016年之后的相关研究成果可能隐含着2E-RP问题领域新的研究趋向，可另行开展分析。需要指出的是，有学者认为2E-VRP问题和2E-LRP问题在本质上是一类问题，也有学者认为TTRP问题只是2E-LRP问题的一种变形[6]。这里暂不深究这四类问题的内在逻辑联系，仍分别梳理学术界针对这四类问题的研究概况;再次，结合其对应的实践背景，分析既有与2E-RP问题相关模型的可延伸或拓展之处;最后，指出2E-RP问题在建模方面的后续研究方向。

二、实践背景

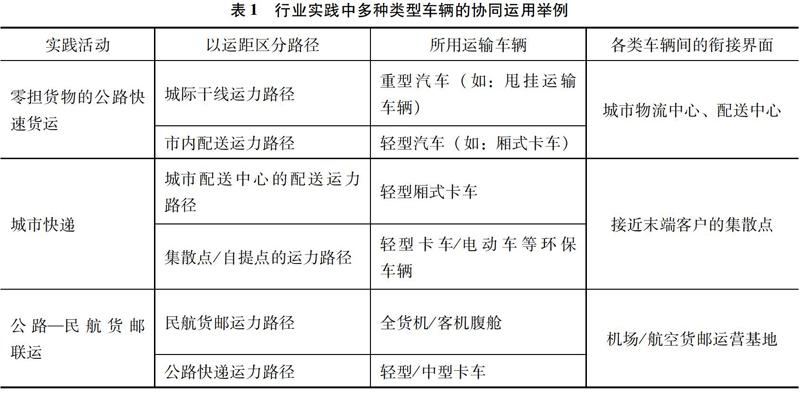
综合运用多样化的、载运能力差异明显的运输工具，有利于物流成本的节约和优化[7]，更有助于科学平衡物流服务水平和物流成本节约之间的背反关系。实际上，多类型的车辆运力的综合调度工作在物流行业实务操作过程中的边界是模糊的，如：京东商城自2012年开始配备干线运力，开始了“仓储+干线运输+城市配送”式的全国性配送网络体系建设过程;亚马逊通过大型配送中心将分散的、小批量多批次的订单需求予以集中，再借助大型物流企业的运营网络实现统筹配送的规模效应;苏宁在全国开通贯穿主要城市的定点干线运输，实现不同城市仓储商品的统筹调拨，同时结合便捷的末端配送，确保物流服务时效性。再如，多式联运是综合调度多种类型车辆运力的典型表现形式，在欧洲中部和西南部多个国家，多式联运物流中心数量增长快速[8]，这从一个侧面说明综合运用多种类型车辆运力的广泛性。表1列举了在行业实践中多种类型车辆综合运用的若干例子。

無论从企业实践还是从学术研究看，均可从层级化物流网络的视角审视多种类型车辆运力的协同运用问题。不同层级网络上可使用不同类型的车辆运力，是多级物流网络获得成本优势的保障条件[9]。物流网络上的车辆运输活动可分为点点直达运输和多级配送运输，其中多级配送运输主要表现为带仓库多级配送、分拨配送[10-11]等。物流网络的层级越多，涉及的货物中转、换装、仓储等环节越多，这并不利于保障货物流转速度。以分拨作业为例，其能够在相对普遍的范围内被采用，主要是由于分拨作业模式可提高时效性和客户满意度[12]、降低库存。此外，从待运货物批量规模的角度，可分为整车运输和零担运输，这两类货运活动往往并存于同一物流网络中。

三、既有相关研究综述

（一）2E-VRP问题

1. 问题界定和主要模型

在基本2E-VRP问题（也被称为2E-CVRP问题）中，两级物流网络上设有一个中心场站和固定数量的有作业能力限制的中转站;两个层级网络上分别使用确定数量的某类车辆，每一中转站可运用的车辆数量是待定的;所有客户点的需求固定且已知，需求不能分割。问题的求解目标是在车辆载重能力的约束下满足客户点的物流需求，且使总成本最小。

2E-VRP问题数学模型的变量一般有三类：① 描述网络上某条弧是否有车辆通过的整数变量;② 确立客户点与中转站间指派关系的二进制变量;③ 描述货物流经某一弧情况的连续变量。目标函数为运输成本和中转站作业成本之和的最小化。约束条件主要包括：客户点与中转站之间的指派关系约束;车辆路径闭合;中转站的作业能力限制;可用车辆总数限制;中转站的货物发送量等于其所服务的客户点货运需求总量;等等。

Perboli et al.[13-14]补充了求解2E-VRP问题数学模型的有效不等式，该类有效不等式可描述路径与弧变量之间的相互关系，将刻画可行解连通性与可行性的有效不等式作为边缘割约束添加到模型中以强化模型的下界。Jepsen et al.[15]指出Perboli等[14]提供的数学模型在中转站数量超过两个的情况下可能给出不正确的上界，并提出一种边界流模型。通过算例测试，在中小规模的算例中，针对Jepsen et al.[15]模型的算法都体现出良好的运算效果。Crainic et al.[16]研究客户点分布、中转站位置与数量、中转站可达性、中转站和客户点之间的运输成本对目标函数的影响。研究结果表明，当客户点数量与中转站数量的比值在20～25之间时，有利于获得最小成本。在达到最小成本之前，开通中转站可减少总成本，达到最小成本之后，新增中转站会使得总成本有所增加。此外，若场站位于客户點区域的外部，中转站位于这两者之间，总成本的计算结果较一般VRP问题能体现出一定优势。Crainic et al.[17]分析了装卸作业、环境、拥堵等多种因素对中转站布局的影响，比较了两级配送网络模式与单级配送网络模式的效果。研究结果表明，当市区范围内的路段实时成本增加时，中转站的使用方案会有较大的改变，建议在下午执行配送操作以避免交通拥堵。

Baldacci et al.[18]将各种车辆的固定成本考虑在内，提出另一种形式的2E-VRP问题数学模型，分别设定第一级网络和第二级网络上的路径集合，采用二进制变量分别表示不同层级上的可行路径是否为最终解所采用，采用非负整数变量表示由第一层级车辆配送到某中转站的货物量。通过对基准算例的运算测试，本文所采用的精确算法在所能求解的算例规模与运行时间上都较其他精确算法有一定提高。Soysal et al.[19]将分时段分弧段的交通拥堵因素加入到2E-VRP问题中，将驾驶员成本和车辆油耗考虑在内，设定第一层车辆在行驶中保持自由流速度，第二层车辆的行驶速度受时段和区段影响。该文提出了采用不同目标函数的多种模型，测试了与距离、时间、油耗、成本相关的关键指标。运算结果表明，运用两级配送系统可提供低成本的配送解决方案。

Gonzalez-Feliu[10]和Perboli et al.[14]对2E-VRP问题基本形式及拓展形式进行了梳理。2E-VRP问题的拓展形式包括：① 带时间窗的2E-VRP问题，同时考虑中转站的配送服务时间窗和虑客户点时间窗;② 带中转换装时间约束的2E-VRP问题，要求在中转站换装作业时间窗内应当有第二层级车辆备用;③ 带回程货的2E-VRP问题，允许中转站同时作为配送货物和回程货物的中转换装点;④ 多场站的2E-VRP问题，允许有多个中心场站;⑤ 带直接配送的2E-VRP问题，允许中心场站直接为其客户点提供配送服务。

2.求解方法

精确算法多针对基本2E-VRP问题。Perboli and Tadei[13]将有效不等式嵌入到分支定界框架中，所用算例最多包含50个客户点，求解结果相对于已知最优解优化了4%～15%。Perboli et al.[14]以中转站和客户点间指派关系的搜索为求解关键，所用算例最多包含50个客户点和4个中转站。Santos et al.[20]使用两种分支定价法，一种是基于路径的，它需要满足初等性条件，另一种考虑了q-路径。算例中客户点的数量最多为51个。Jepsen et al.[15]应用分支定界法，获得93个测试算例中47个算例的新的最优解，该算法要优于之前的精确算法。Santos et al.[21]基于分支定界定价法，增设几类有效不等式，获得了基准算例的若干个新的最优解和上限解。算例运算结果表明，该算法比之前的精确算法更好。Baldacci et al.[18]基于动态规划提出双重上升方法和一种将基本2E-VRP问题分解为一组多场站有容量限制VRP问题的精确算法，所用算例最多包含100个客户点和6个中转站，获得了153个算例中144个算例的最优解，所采用的精确算法在所能求解的算例规模与运行时间上都较其他精确算法有一定改善。Sitek and Wikarek[11]将约束逻辑规划和数学规划结合起来进行求解，用66个小规模算例进行测试，在求解规模与效率上都有所提升。

求解2E-VRP问题的启发式算法类型多样。Crainic et al.[22]首先求解第二层级的VRP问题，再据此构建第一层级的车辆路径;第一层的路径方案又反作用于第二层路径的优化设计。该文献的运算实验表明，两级配送网络模式能明显降低配送成本。Crainic et al.[23]使用Multi-start启发式方法，邻域搜索被用于建立可行解，在确立客户点和中转站指派关系时采用随机扰动，所用算例最多包含50个客户点和5个中转站。Wang et al.[24]采用的混合蚁群算法包括三部分：应用聚类将原问题划分为若干个VRP问题，应用多邻域衰减策略改进蚁群算法求解子问题，应用基于阈值的局域搜索对可行解进行优化;所用算例规模在20～50个客户点。Hemmelmayr et al.[25]使用自适应大规模邻域搜索算法，针对基准算例的计算结果表明该算法好于既有的一些算法。Zeng et al.[26]使用嵌入了“先路径后聚类”算法的贪婪随机自适应程序（GRASP）和变邻域下降（VND）方法。GRASP的分离算法将随机生成的所有客户点序列分离，将客户点分配给中转站，直到合理分配方案出现;VND则对可行解进行优化。从三组基准算例的运算结果看，该算法是有效的，且优于之前的其他算法。何江和黄翰[27]使用基于贪婪算法、蚁群算法和邻域搜索算法的混合启发式算法，22个基准算例和3个大规模算例的计算结果表明，该算法在保证较高精确性的同时具有较高求解效率。林镇泽[28]使用基于大规模邻域搜索的改进人工蜂群算法，对Perboli et al.[14]和Hemmelmayr et al.[25]提供的算例进行运算。计算结果表明，该算法对VRP问题有较强的搜索性能，当客户点数量比较多时，改进后的算法与原算法相比更稳定、性能表现更好。

（二）2E-LRP问题

1. 问题界定和主要模型

在基本2E-LRP问题中，两级物流网络上设有单个或者多个中心场站和若干备选的、有能力限制与开通成本的中转站;两个层级网络上分别使用数量待定的某种车型;所有客户点的需求是已知的，需求不能分割;设定中心场站和中转站的能力能够满足所有客户点需求，需确定拟开通的中转站和中心场站（多中心场站情景下）、各级网络上的车辆路径方案。

既有研究给出了2E-LRP问题数学模型（如Nguyen et al.[29-30]），以Nguyen et al.[30]构建的单中心场站情景下2E-LRP问题模型为例：两级物流网络上有1个中心场站、m个可选用的中转站和n个客户点;在中心场站处保有第一层网络的车辆，所有中转站共享第二层网络的车辆;考虑车辆固定成本，车辆数量待定;设定中心场站和中转站的容量能够满足所有客户点的总需求。模型涉及变量包括：中转站开通与否的二进制变量;中轉站与客户点对应关系的二进制变量，表达车辆途经弧次数的整数变量。目标函数是寻求中转站开通成本、各类车辆的固定成本和运行成本总和的最小化。约束条件包括：所用车辆数量限制;车辆路径闭合;中转站作业能力约束;等等。

Boccia et al.[31]较早针对多中心场站的情景，考虑了选址、不同类型车辆、不同类型的车队规模和两层网络中路径之间的联系等因素。采用禁忌搜索算法对各类算例进行了测试，结果表明所提出的算法对大多数算例是有效的。而Contardo et al.[32]给出了该类问题的车辆流模型，兼顾不同中心场站的作业能力限制和开通成本。对算例的求解运算结果表明，所采用的分支切割算法能在合理时间内求解中小型规模的算例，自适应大规模邻域搜索算法能较快找到大规模算例的满意解，且优于之前的算法。Dalfard et al.[33]兼顾车队规模、车辆行驶路径长度等约束，以及中转站处理货物时的变动成本，所构建的非线性规划模型对大规模问题非常有效，所提出的两阶段启发式算法能在较短时间内给出高质量的解。Rahmani et al.[34]兼顾多类型产品、集配货一体的情景，目标函数中包括选址与路径两类成本。提出了两类邻域搜索算法，分别用来优化路径与选址，分析了邻域搜索算法的Multi-start策略。Winkenbach et al.[35]兼顾城市物流过程中货物整合与配送外包、运输方式选择等因素，构建混合整数线性规划模型描述2E-LRP问题的一种拓展形式。时间窗约束也在2E-LRP问题中有所体现。如：Nikbakhsh and Zegordi[36]建立了带软时间窗约束2E-LRP问题（2E-LRP STW问题）的四下标数学模型，目标函数增加了违反客户点软时间窗的惩罚成本，提出一种启发式算法来提供模型的下界。Govindan et al.[37]针对有明显时效要求的易腐食品供应链网络，提出2E-LRP TW问题，兼顾软时间窗但不考虑直接配送。文中提出了多目标混合启发式算法，并与既有的多目标遗传算法进行求解效果对比。

2.求解方法

个别文献采用了精确算法。如：Contardo et al.[32]采用分支定界法和自适应大邻域搜索启发式方法求解147个算例（中心场站数从2个到5个不等，中转站数从3个到20个不等，客户点数从8个到200个不等），计算结果表明分支定界法能够提供紧下限。Diabat Theodorou[38]将2E-LRP问题的非线性混合整数规划模型转换为能够用CPLEX求解的混合整数规划模型。通过运算实验说明CPLEX求得的解与既有文献的解是相同的。金莉等[39]采用嵌入拉格朗日启发式算法的分支定界法，使用4组测试算例（最多包含5个备选仓库、10个备选零售点和200个客户点）进行了算例求解测试，测试结果证明该方法是有效的。

迄今用于求解2E-LRP问题的方法多数是启发式算法。Boccia et al.[31]将问题分解为两级子问题，应用禁忌搜索算法对30个算例进行求解（中心场站数为5个，中转站数从8个到20个不等，客户点数从50个到200个不等），结果表明该算法对大多数算例是有效的。Nguyen et al.[40]综合了GRASP和进化/迭代邻域搜索（ELS/ILS），以及禁忌表。GRASP轮流采用三种构造启发式方法生成初始解，再由ELS/ILS进行优化。对基准算例的求解运算表明，该算法优于既有文献的求解结果。Nguyen et al.[29]使用Multi-start迭代邻域搜索（简写为MS-ILS），循环使用三种贪婪随机启发式方法获得初始解。MS-ILS可通过路径重连程序（PR）进行内部优化或再优化。运用该算法求解了114个算例（客户点数最多为200个，中转站数最多为5个）。Nguyen et al.[30]提出GRASP结合学习进程（LP）和PR，GRASP和LP使用三种贪婪随机启发式方法用来生成试探解，使用两种变邻域下降程序进行优化，可选择的PR通过结合强化策略和后优化增加了一种记忆机制;选用的算例与Nguyen et al.[29]的前三组算例相同。算例运算结果表明该算法优于单一的启发式算法。Vidovi c' et al.[41]运用启发式算法求解了以利润最大化为目标、兼顾多个作业周期的2E-LRP问题混合整数规划模型，使用随机生成的算例验证算法有效性。Wang and Mu[42]综合运用模拟退火和PR，针对84个基准算例（中心场站数为1个到5个不等，中转站数从9个到20个不等，客户点数从20个到200个不等）的运算结果显示了该算法的有效性。

Dalfard et al.[33]应用混合遗传算法和模拟退火算法求解带车辆总数约束和车辆路径长度约束的2E-LRP问题，使用20个随机算例（中心场站数量从3个到10个不等，中转站数量从10个到50个不等，客户点数量从25个到100个不等）进行算法测试，运算结果表明该算法能在较短时间内给出高质量的解。Wang et al.[43]将2E-LRP问题的需求拓展为模糊需求，采用改善的遗传算法予以求解，实验结果表明模型与算法对车辆分配与车辆路径问题均是有效的。Rahmani et al.[34]使用邻域搜索分别对车辆路径和中转站选址进行优化，使用2-Opt策略应对多产品和集/配货约束，算例测试显示该策略可给出质量更好的解、但耗时更多。金莉等[44]采用遗传算法，使用整数编码的三级染色体编码结构，并在交叉和变异操作中引入禁忌搜索算法，算例包含5个备选仓库、10个备选零售点及20和40个客户点。

Nikbakhsh and Zegordi[36]使用启发式算法求解2ELRPSTW问题，通过搜索六个邻域对初始解进行优化，并使用21个随机算例（中心场站最多10个，中转站最多50个，客户点最多100个）对算法进行测试，运算结果印证了该算法的有效性。Govindan et al.[37]结合多目标粒子群优化和自适应多目标变邻域搜索来求解2E-LRPTW问题，构建12个算例（最多包含12生产厂、18个配送中心和30个客户点），并与既有的多目标遗传算法进行求解效果对比，表明本文所提出算法的求解效果更优。

3.TTRP问题

TTRP问题可描述为：在物流网络上，一些客户点既可以由汽车列车（卡车加挂全挂车）服务，也可以由单独的卡车服务，而有些客户点仅能由卡车提供服务;设定卡车和挂车数量已知。问题求解目标是寻找成本最低的车辆路径方案，这些路径的起讫点都在中心场站，每个客户点都只被提供1次服务。[45]

TTRP问题的基本形式是：运输网络上有一个中心场站和若干客户点，客户点分为两类：一类是卡车客户点（简称TC），只允许卡车进行配送;另一类是汽车列车客户点（简称VC），既允许汽车列车又允许卡车进行配送。车辆路径分为三类：第一类为PTR，路径中的客户点（可以同时包含VC和TC）均由卡车进行配送;第二类为PVR，路径中的客户点（只包含VC）均由汽车列车进行配送;第三类为CVR，路径包含一条主路径（只包含VC）和至少一条以主路径上某一客户点为起止点的子路径（可以同时包含VC和TC）。中心场站上保有不同载重能力、不同数量的卡车和挂车，可行车辆路径要满足车辆载重能力约束。[46-47]问题求解目标是路径总长度最小化。个别文献采用精确算法来求解TTRP问题，如：Belenguer et al.[48]给出了带卫星站的单一卡车全挂车TTRP问题的整数规劃模型，提出收紧该模型的几类不等式，并运用分支定界法进行求解，既有算法的求解能力局限在中转站最多为10个、客户点最多为50个，该文的求解规模可扩大到20个中转站与100个客户点。

用于求解TTRP问题的启发式算法主要有：① 以禁忌搜索算法为主。Semet and Taillard[49]使用禁忌搜索对实践算例进行求解，涉及21台卡车与7台挂车的路径，运算实验证明禁忌搜索能在短时间内获得算例的解，该解优于之前的实践方案。Chao[46]提出两阶段算法：构造算法和禁忌搜索优化，并在算法中融入确定性退火偏差概念;构建了21个TTRP测试算例（客户点规模为50～199个），测试结果表明该算法是有效的。Scheuerer[50]提出两种构造算法，采用禁忌搜索予以优化，对禁忌搜索的各个参数进行灵敏度分析，并对Chao[46]提供的21个算例进行求解，算例运算结果有进一步的改进。② 以模拟退火算法为主。Lin et al.[45]使用模拟退火算法在针对21个基准算例的计算结果中，有11个新的最优解和6个已知的最优解。此外，Lin et al.[51]和Lin et al.[52]分别应用模拟退火算法对放松车辆数约束的TTRP问题和带时间窗的TTRP问题进行求解，与既有结果相比，解的优化率约为5%。③ 以邻域搜索算法为主。Villegas et al.[53]综合运用贪婪随机自适应、变邻域搜索和先路径后聚类的方法，也采用21个基准算例，计算结果表明该综合化算法的优化结果要好于已知最优结果。Villegas et al.[54]综合运用贪婪随机自适应和迭代邻域搜索算法来获得局部最优解，采用两组测试算例，其中一组是既有的21个基准算例，另一组是来自Lin et al.[51]提供的36个随机算例，结果表明该文提供的算法能够得到与既有最优结果十分相近的结果，但求解速度要快于既有算法。

4.VRPCD问题

在VRPCD问题[12]中，每辆车都属于分拨中心，且不允许分割配送;车辆运行分为集货运输和配送两个过程，在分拨中心实施货物的中转换装作业。问题求解目标是确定所使用的车辆数、车辆运行路线、每辆车到达分拨中心的时间，寻求运输成本最小化，有些研究也兼顾分拨中心的时间窗。

在Dondo et al.[55]所研究的供应链VRP问题（VRP-SCM问题）及其整数线性规划基础上，Dondo et al.[9]增加分拨作业环节，提出VRPCD-SCM问题，考虑多种商品，且允许采用货物从工厂直接运输到客户点和通过分拨中心运输到客户点等多种形式。该文基于混合整数规划模型提出了整体的优化框架，并对算例进行了测试，均能在在合理的时间内得到优化解。Ahmadizar et al.[56]将同一产品来源地多样化、产品价格差异化等因素考虑在VRPCD问题中。Moghadam et al.[57]研究带时间窗且客户需求可分割的VRPCD问题，取、送货必须满足时间窗要求，配送过程中客户点的需求可以由多辆车辆承担;目标函数涵盖车辆行驶成本和分拨中心的换装时间。通过对不同数据集的测试，实验结果证明文中所采用的混合算法优于既有文献中的模拟退火算法。

Lee et al.[12]应用禁忌搜索算法求解VRPCD问题，随机算例最多包含50个点。采用枚举法获得最优解来比较禁忌搜索算法显示，禁忌搜索算法得到的解与最优解的误差在5%以内。Ahmadizar et al.[56]结合遗传算法和邻域搜索来求解VRPCD问题的混合整数非线性规划模型，并利用算例验证了算法的有效性。Morais et al.[58]提出三种迭代邻域搜索算法ILS，一种为标准ILS，第二种在迭代过程保留精英解，第三种采用基于整数规划的程序进行强化;对既有算例（最多包含200个OD对）进行求解，得到一半数量算例的新的最优解。Moghadam et al.[57]结合蚁群算法和模拟退火求解带时间窗且需求可分割的VRPCD问题，使用的算例最多包含200个OD对。通过对不同算例集的测试，表明该文所采用的混合算法优于既有文献中的模拟退火算法。

四、 既有模型的局限

（一）既有模型与应用背景的对照

有学者针对既有研究中所界定的2E-VRP问题和2E-LRP问题提出以下疑义：网络上货物最根本的来源是哪里？[59]既有研究往往假设中心场站的货物供应量是足够的，这一假设无形中忽视了本该存在于网络上的更高层次的另一类物流运输过程。

从实践看，最接近消费地的物流节点（如配送中心）的商品品类繁多、且往往来源于多个异地[14]，由最初来源地到配送中心一般采用整车运输[60]。也即，货物的供应源通常是制造商/工厂，或是将不同产品由工厂集中于一处的高层次的场站，这个初始的、规模化供应过程一般采用整车运输[61]。然而，既有2E-RP问题一般只考察两个或更多個相互衔接的零担运输环节，并没有将整车运输考虑在内。既有研究所关注的零担运输多级网络通常应用于区域配送或城市物流配送领域，且认为网络上的配送中心要能够暂存货物，能够供长途货车卸货、末端配送车装货[14]，但建模过程并没有考虑长途货车运量大、运距长与配送车运量小、运距短的差异。

资源禀赋的空间分布和社会分工细化进程使产地、消费地之间的时空分离现象更加显著。实际上，跨区域物流网络所承担的运量要占据较大的比例，如：自2007年有统计数据以来，我国同城快递和异地快递业务量（包括国内异地及国际）占快递总量的比例分别保持在24%左右和76%左右。这从一定程度上要求学术研究工作应注意兼顾面向城际干线运输活动的车辆路径和面向城市配送的车辆路径。

（二）既有建模思路

若中转站选址及其所服务的客户点已确定，则2E-RP问题可分解为若干个VRP问题。从既有研究看，建模关键在于如何使得网络上不同层级的车辆路径衔接和互动起来[10][15]。

既有模型是以中转站选址或中转站所服务的客户点集的变化为关键衔接。中转站选址实际上是决策中转站的货物中转量是否为0，使中转站所服务客户点集发生变化实际上是促使中转站的货物中转量发生变化。从本质上看，既有模型是以中转站的货物中转量的规模变化为建模关键。正是由于中转站的货物中转量是变量，才使得数学规划模型有了可行域。从两级物流网络的构成要素看，除了中转站这一基本资源，车辆运力是另一类基础资源，如果能够将不同层级的车辆路径以运力的协同使用为关键衔接，有望拓展既有建模思路。

此外，既有模型设定第一级的运输活动要与第二级的运输活动相似，但较第二级的运输活动要更简化[29]，也即：两个层级上均为配送活动，站点及其辐射服务点之间在数量上体现为“一对多”关系，第一级网络上由一个场站服务多个中转站，第二级网络上由一个中转站服务多个客户点。实际上，第一级的运输活动往往并非简单的配送，中转站之间也可能有货物交流[61]，即第一级网络上节点间物流需求可体现为“多对多”式需求。不同层级上物流需求特征的不同将影响数学模型的形式。

五、 后续研究的拓展方向

对比分析2E-RP问题及VRP问题相关研究成果的问题界定、模型构建、运算试验等，不难发现：第一，VRP问题主要定位于局域运输、末端配送领域[62]，即使是在2E-RP问题的两级物流网络上，不同层级的车辆路径表现出很大的相似性、仍主要体现为“一站服务多点”的配送路径。兼顾城际干线运输与城市内配送于一个网络上的不同类型车辆路径问题研究工作显得很薄弱;第二，针对2E-RP问题研究工作的建模方式相对单一，即都是以中转节点上货物中转量的变化作为确保不同层级上车辆路径互动的关键，这也是既有数学规划模型的建模关键。鉴于两级物流网络上有更多的、值得优化运用的物流资源，可寻求促使两个层级路径互动起来的新的驱动因素，以丰富和拓展建模方式。例如：参考VRPCD问题所对应的企业实务操作方式，考虑在中转节点上货物中转量不发生变化的条件下，采用时效因素、运力匹配因素来确保不同层级上车辆路径的互动联系。

由既有研究成果对于2E-RP问题建模的局限来看，可得出以下启示。

（1）物流活动主要由消费需求激发，消费需求在不同层级物流网络上传递。同一消费点需要的产品可由分布于不同地点的生产者提供，消费点需要的同种产品也可由多个不同的生产者提供[55]。社会分工使各个生产部门之间进行联系，由于分布在不同的经济地理区域，部门之间的联系表现为空间上的种种联络路线。经济活动的专业化分工及其空间分布，与空间运输联系及运输网络布局之间存在密切的互动关系[63]。2E-RP问题中物流需求网络的构建应以消费需求为驱动。由此，2E-RP问题的物流网络可分为城际干线整车运输层和城市内零担配送层。每个城市均可以是一种或多种类型货物的货源地，客户点需求由中转站予以满足。城际干线整车运输层的节点间表现为“多对多”物流需求，城市内零担配送层的节点间表现为“一对多”物流需求。

（2）若干学者认为，选址是长期的、战略性问题，车辆路径优化是短期的、操作性问题，选址、路径这两个子问题不在同一个战略层面[55][60][64]。这里提出运用时效因素和运力匹配因素形成新的2E-RP问题模型，其中不涉及选址问题。

第一，以物流服务时效为建模过程中两级网络车辆路径方案互动的关键衔接因素，充分运用可表征时效的参量[65-67]。在这类新的2E-RP问题模型中，第一、二级网络的车辆路径之间的衔接关键为中转站上的干线运力和配送运力到发时刻之间的差异。设定每个客户点有明确的时间窗要求，一旦拟定好第二级网络的车辆路径方案，就确定了第一级网络上承载不同货物的干线运力应当到达中转站的最迟时间（须预留货物在不同车辆间的中转换装时间）。将中转站上干线运力和配送运力到发时刻之间的差异量化为车辆等待时间惩罚成本，则可驱动混合整数规划模型的构建。

第二，既有2E-RP问题相关研究一般设定同一层级网络上所使用车辆类型是相同的。如果放松这个设定，即同一层级网络所使用的车辆类型是多样的，则可充分运用运力匹配的要求来实现两级网络车辆路径方案的互动。在第二级网络上，使用不同类型的车辆开展配送服务;一旦确立了第二级网络上的车辆类型及其路径方案，就可确定第一级网络上承载不同货物的不同类型的干线运力应当到达中转站的最迟时间。这样，可运用时效要求和运力匹配要求来开展2E-RP问题建模。

（3）既有研究中2E-RP問题的目标函数一般为成本类，如总成本、总运距。随着应对气候变化和物流运输节能减排战略的普遍实施，将碳排放因素纳入VRP问题模型中成为近年来学术研究工作的一个热点。若能在2E-RP问题的目标函数中兼顾碳排放因素，则可对比研究经济效益和社会效益目标对不同类型车辆的配置要求，对比分析不同类型运力配置方式的节能减排效果。

参考文献：

[1]DANTZIG G B， RAMSER J H. The truck dispatching problem [J]. Management science， 1959， 6（1）： 80-91.

[2]BALDACCI R， TOTH P， VIGO D. Recent advances in vehicle routing exact algorithms [J]. 4OR， 2007， 5（4）： 269-298.

[3]LAPORTE G. Fifty years of vehicle routing [J]. Transportation science， 2009， 43（4）： 408-416.

[4]CRAINIC T G， RICCIARDI N， STORCHI G. Advanced freight transportation systems for congested urban areas [J]. Transportation research Part C： Emerging technologies， 2004， 12（2）： 119-137.

[5]CRAINIC T G， RICCIARDI N， STORCHI G. Models for evaluating and planning city logistics systems [J]. Transportation science， 2009， 43（4）： 432-454.

[6]CUDA R， GUASTAROBA G， SPERANZA M G. A survey on two-echelon routing problems [J]. Computers & operations research， 2015， 55： 185-199.

[7]WU T H， LOW C， BAI J W. Heuristic solutions to multi-depot location-routing problems [J]. Computers & operations research， 2002， 29（10）： 1393-1415.

[8]RICCIARDI N， TADEI R， GROSSO A. Optimal facility location with random throughput costs [J]. Computers & operations research， 2002， 29（6）： 593-607.

[9]DONDO R， MNDEZ C A， CERD J. The multi-echelon vehicle routing problem with cross docking in supply chain management [J]. Computers & chemical engineering， 2011， 35（12）： 3002-3024.

[10]GONZALEZ-FELIU J. Two-echelon transportation optimisation： a meta-narrative analysis [J]. WPOM-Working papers on operations management， 2011， 2（1）： 18-30.

[11]SITEK P， WIKAREK J. A novel integrated approach to the modelling and solving of the two-echelon capacitated vehicle routing problem [J]. Production & manufacturing research， 2014， 2（1）： 326-340.

[12]LEE Y H， JUNG J W， LEE K M. Vehicle routing scheduling for cross-docking in the supply chain [J]. Computers & industrial engineering， 2006， 51（2）： 247-256.

[13]PERBOLI G， TADEI R. New families of valid inequalities for the two-echelon vehicle routing problem [J]. Electronic notes in discrete mathematics， 2010， 36： 639-646.

[14]PERBOLI G， TADEI R， VIGO D. The two-echelon capacitated vehicle routing problem： models and math-based heuristics [J]. Transportation science， 2011， 45（3）： 364-380.

[15]JEPSEN M， SPOORENDONK S， ROPKE S. A branch-and-cut algorithm for the symmetric two-echelon capacitated vehicle routing problem [J]. Transportation science， 2013， 47（1）： 23-37.

[16]CRAINIC T G， PERBOLI G， MANCINI S， et al.. Two-echelon vehicle routing problem： a satellite location analysis [J]. Procedia-social and behavioral sciences， 2010， 2（3）： 5944-5955.

[17]CRAINIC T G， MANCINI S， PERBOLI G， et al. Impact of generalized travel costs on satellite location in the two-echelon vehicle routing problem [J]. Procedia-Social and behavioral sciences， 2012， 39： 195-204.

[18]BALDACCI R， MINGOZZI A， ROBERTI R， et al. An exact algorithm for the two-echelon capacitated vehicle routing problem [J]. Operations research， 2013， 61（2）： 298-314.

[19]SOYSAL M， BLOEMHOF-RUWAARD J M， BEKTA T. The time-dependent two-echelon capacitated vehicle routing problem with environmental considerations [J]. International journal of production economics， 2015， 164： 366-378.

[20]SANTOS F A， DA CUNHA A S， MATEUS G R. Branch-and-price algorithms for the two-echelon capacitated vehicle routing problem [J]. Optimization letters， 2013， 7（7）： 1537-1547.

[21]SANTOS F A， MATEUS G R， DA CUNHA A S. A branch-and-cut-and-price algorithm for the two-echelon capacitated vehicle routing problem [J]. Transportation science， 2014， 49（2）： 355-368.

[22]CRAINIC T G， MANCINI S， PERBOLI G， et al. Clustering-based heuristics for the two-echelon vehicle routing problem [DB/OL]. CIRRELT， Montréal， CIRRELT-2008-46 http：//www.cirrelt.ca/DocumentsTravail/ CIRRELT-2008-46. pdf.

[23]CRAINIC T G， MANCINI S， PERBOLI G， et al. Multi-start heuristics for the two-echelon vehicle routing problem [M]. Berlin：Springer Berlin Heidelberg，2011， 179-190.

[24]WANG M， TIAN X， WU S. Hybrid ant colony optimization algorithm for two echelon vehicle routing problem [J]. Procedia engineering， 2011， 15： 3361-3365.

[25]HEMMELMAYR V C， CORDEAU J F， CRAINIC T G. An adaptive large neighborhood search heuristic for two-echelon vehicle routing problems arising in city logistics [J]. Computers & operations research， 2012， 39（12）： 3215-3228.

[26]ZENG Z Y， XU W， XU Z Y， et al. A hybrid GRASP+ VND heuristic for the two-echelon vehicle routing problem arising in city logistics [J]. Mathematical problems in engineering， 2014（1）：1-11.

[27]何江，黃翰.双层车辆路径问题的混合启发式算法[J].计算机应用研究，2013，30（2）：350-353.

[28]林镇泽.求解双层车辆路径问题的改进人工蜂群算法[D].广州：华南理工大学，2014.

[29]NGUYEN V P， PRINS C， PRODHON C. A multi-start iterated local search with tabu list and path relinking for the two-echelon location-routing problem [J]. Engineering applications of artificial intelligence， 2012， 25（1）： 56-71.

[30]NGUYEN V P， PRINS C， PRODHON C. Solving the two-echelon location routing problem by a GRASP reinforced by a learning process and path relinking [J]. European journal of operational research， 2012， 216（1）： 113-126.

[31]BOCCIA M， CRAINIC T G， SFORZA A， et al. A metaheuristic for a two echelon location-routing problem[M]//BOCCIA M，CRAINICT G，SFORZA A，et al. Experimental Algorithms. Berlin：Springer Berlin Heidelberg， 2010， 288-301.

[32]CONTARDO C， HEMMELMAYR V， CRAINIC T G. Lower and upper bounds for the two-echelon capacitated location-routing problem [J]. Computers & operations research， 2012， 39（12）： 3185-3199.

[33]DALFARD V M， KAVEH M， NOSRATIAN N E. Two meta-heuristic algorithms for two-echelon location-routing problem with vehicle fleet capacity and maximum route length constraints [J]. Neural computing and applications， 2013， 23（7-8）： 2341-2349.

[34]RAHMANI Y， CHERIF-KHETTAF W R， OULAMARA A. A local search approach for the two-echelon multi-products location-routing problem with pickup and delivery [J]. IFAC-PapersOnLine， 2015， 48（3）： 193-199.

[35]WINKENBACH M， KLEINDORFER P R， SPINLER S. Enabling urban logistics services at La Poste through multi-echelon location-routing [J]. Transportation science，2016，50（2）：363-761.

[36]NIKBAKHSH E， ZEGORDI S H. A heuristic algorithm and a lower bound for the two-echelon location-routing problem with soft time window constraints [J]. Scientia iranica transaction E： industrial engineering， 2010， 17（1）： 36-47.

[37]GOVINDAN K， JAFARIAN A， KHODAVERDI R， et al. Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food [J]. International journal of production economics， 2014， 152： 9-28.

[38]DIABAT A， THEODOROU E. A location–inventory supply chain problem： reformulation and piecewise linearization [J]. Computers & industrial engineering， 2015， 90： 381-389.

[39]金莉，朱云龍，申海.三级物流网络选址-路径问题建模与求解算法研究[J].控制与决策，2010，25（8）：1195-1206.

[40]NGUYEN V P， PRINS C， PRODHON C. A multi-start evolutionary local search for the two-echelon location routing problem [M]// BLESAM J，BLUM C，RAIDL G，et al. Hybrid Metaheuristics. Berlin：Springer Berlin Heidelberg， 2010， 88-102.

[41]VIDOVIC' M， RATKOVIC'B， BJELIC'N， et al. A two-echelon location-routing model for designing recycling logistics networks with profit： MILP and heuristic approach [J]. Expert systems with applications， 2016， 51： 34-48.

[42]WANG C， MU D. Design of the distribution network for a “collect-on-delivery” company in a metropolitan context using simulated annealing with path relinking [J]. Applied mathematics & information sciences， 2015， 9（3）： 1529-1539.

[43]WANG S， MA Z， ZHUANG B. Fuzzy location-routing problem for emergency logistics systems [J]. Computer modelling & new technologies， 2014， 18（2）： 265-273.

[44]金莉，朱云龍，申海，等.集成三级物流系统的网络规划问题研究[J].计算机应用研究，2010，27（9）：3287-3289.

[45]LIN S W， VINCENT F Y， CHOU S Y. Solving the truck and trailer routing problem based on a simulated annealing heuristic [J]. Computers & operations research， 2009， 36（5）： 1683-1692.

[46]CHAO I M. A tabu search method for the truck and trailer routing problem [J]. Computers & operations research， 2002， 29（1）： 33-51.

[47]LI H， LU Y， ZHANG J， et al. Solving the tractor and semi-trailer routing problem based on a heuristic approach [J]. Mathematical problems in engineering， 2012.

[48]BELENGUER J M， BENAVENT E， MARTNEZ A， et al.. A branch-and-cut algorithm for the single truck and trailer routing problem with satellite depots [J]. Transportation science，2016，50（2）：363-761.

[49]SEMET F， TAILLARD E. Solving real-life vehicle routing problems efficiently using tabu search [J]. Annals of operations research， 1993， 41（4）： 469-488.

[50]SCHEUERER S. A tabu search heuristic for the truck and trailer routing problem [J]. Computers & operations research， 2006， 33（4）： 894-909.

[51]LIN S W， VINCENT F Y， CHOU S Y. A note on the truck and trailer routing problem [J]. Expert systems with applications， 2010， 37（1）： 899-903.

[52]LIN S W， VINCENT F Y， LU C C. A simulated annealing heuristic for the truck and trailer routing problem with time windows [J]. Expert systems with applications， 2011， 38（12）： 15244-15252.

[53]VILLEGAS J G， PRINS C， PRODHON C， et al. A GRASP with evolutionary path relinking for the truck and trailer routing problem [J]. Computers & operations research， 2011， 38（9）： 1319-1334.

[54]VILLEGAS J G， PRINS C， PRODHON C， et al. A matheuristic for the truck and trailer routing problem [J]. European journal of operational research， 2013， 230（2）： 231-244.

[55]DONDO R， MNDEZ C A， CERD J. Managing distribution in supply chain networks [J]. Industrial & engineering chemistry research， 2009， 48（22）： 9961-9978.

[56]AHMADIZAR F， ZEYNIVAND M， ARKAT J. Two-level vehicle routing with cross-docking in a three-echelon supply chain： a genetic algorithm approach [J]. Applied mathematical modelling， 2015， 39（22）： 7065-7081.

[57]MOGHADAM S S， GHOMI S F， KARIMI B. Vehicle routing scheduling problem with cross docking and split deliveries [J]. Computers & chemical engineering， 2014， 69： 98-107.

[58]MORAIS V W， MATEUS G R， NORONHA T F. Iterated local search heuristics for the vehicle routing problem with cross-docking [J]. Expert systems with applications， 2014， 41（16）： 7495-7506.

[59]PRODHON C， PRINS C. A survey of recent research on location-routing problems [J]. European journal of operational research， 2014， 238（1）： 1-17.

[60]PERL J， DASKIN M S. A warehouse location-routing problem [J]. Transportation research Part B： Methodological， 1985， 19（5）： 381-396.

[61]SHEN S Y， HONDA M. Incorporating lateral transfers of vehicles and inventory into an integrated replenishment and routing plan for a three-echelon supply chain [J]. Computers & industrial engineering， 2009， 56（2）： 754-775.

[62]VAN DUIN J H R， TAVASSZY L A， TANIGUCHI E. Real time simulation of auctioning and re-scheduling processes in hybrid freight markets [J]. Transportation research Part B： Methodological， 2007， 41（9）： 1050-1066.

[63]李紅启，高洪涛，宋强.货运企业的伪超循环结构及其作用[J].北京交通大学学报（社会科学版），2011，10（3）：34-39.

[64]NAGY G， SALHI S. Location-routing： issues， models and methods [J]. European journal of operational research， 2007， 177（2）： 649-672.

[65]LI H， ZHANG L， LV T， et al. The two-echelon time-constrained vehicle routing problem in linehaul-delivery systems [J]. Transportation research Part B： Methodological， 2016， 94： 169-188.

[66]LI H， YUAN J， LV T， et al. The two-echelon time-constrained vehicle routing problem in linehaul-delivery systems considering carbon dioxide emissions [J]. Transportation research Part D： Transport and environment， 2016， 49： 231-245.

[67]GRANGIER P， GENDREAU M， LEHUD F， ROUSSEAU L M. An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization [J]. European journal of operational research， 2016， 254（1）： 80-91.