细思创新 让学于生
王映
【摘要】未来的关键在于教育,教育的核心乃是人才,人才的培养倚仗创新.创新意识的养成是一个循序渐进的过程,教师恰如其分的点拨起到不可或缺的作用.创新意识的培养,需要从根本上激励和激发学生,调动他们的积极性和主动性.笔者对比中美小学数学课堂,倡导将让学于生融入数学课堂,在教与育中点化生情,在学与习中鼓励质疑.
【关键词】创新意识;对比研究;生本课堂
教育的本质不是简单的知识传授,更重视综合能力的培养.未来的竞争不仅仅是知识间的竞争,更是应变能力、表达能力、创造性思维等综合实力的比拼.因此,在小学数学课堂中要注重提升学生的创新意识,在探究中培养学生求异的思维品质.在探寻创新意识培养的过程中,笔者反复思考:何为创新?何以创新?下面我们基于课题“培养创新素养最有效的中外教学合作模式”,以中美小学数学课堂教学的比较为例,在研究中求新异,整理出几点思考,为今后的探索点亮一盏灯.
一、缘起:浅尝辄止创新难,细思梳理渐明晰
在教改的思潮下,创新意识的培养早已渗入课堂教学之日常,或以教师为着力点,发挥师者之引领示范;或从课堂情境入手,打造思维模式;或从合作探究出发,实现知识构建.不同的研究角度诠释了创新意识的不同维度.然而,烦琐的课业之于坚持创新,成了一块沉重又难以摆脱的巨石,一切美好的整装待发终究归为学科知识的获取,创新默默走向一个浅尝辄止的省略号.所谓“学非探其叶,问必拔其根”,来看这样两个问题:
1.何为创新
创造性思维是指主动开拓新领域、发现新方法、开创新成果的一种思维活动,它是数学能力的核心和关键.创新意识主要指个体对自然中的各种现象怀着强烈的探索意识,在好奇心的驱动下不断求索,并对发现的新问题进行深入详细的探究.就小学生而言,从综合运用已有知识、技能、方法解决未曾遇过的新问题,到大胆质疑、自主探索、反复推敲至新方法、新观点的水到渠成,再到灵活变通,带着发现问题的眼光看待身边的事物,感悟知识本质,形成核心素养,形成数学创新意识,这是一个循序渐进的过程,不似绚烂多彩转瞬即逝的烟火,而是茁壮成长四季常青的青松.这个过程中的每一个阶段,教师恰如其分的點拨将是其不可或缺的沃土.
2.何以创新
课程标准明确指出,创新意识的培养具有十分重要的意义.创新灵感不是与生俱来的.培养创新意识,需要从根本上激励和激发学生,调动他们的积极性和主动性.只有提升学生的学习主动性,激发他们浓厚的学习兴趣,才能以情感态度的养成促进创新思维的生成.塑造创新思维,不乏潜移默化的渗透,得源于新的课堂教学形态:科学合理又层层递进的问题设置,积极向上又和谐民主的学习氛围;由一段“小插曲”引发的头发风暴,讨论中学生敢表达、教师善倾听.当强烈的探索欲望与严谨的逻辑思维融合在一起,创新思维这座由知情意堆砌而成的灯塔将在学海中指引学生奋勇前行.
基于对上述问题的思考,笔者借助国际化办学丰富的资源,对比中美数学课不同的教学方法,探讨创新意识培养方式的变革.
二、探究:中美课堂同对比,细节之中求新异
笔者所在的课题组邀请美国数学教师Mr.George共同参与研究,并执教“A Kind of Review about the Area”,本课选自美国Harcourt版数学六年级教材,主要在现实情境中对长方形、三角形、圆等图形的面积计算进行系统复习.中美数学教材在内容编排上虽略有不用,但数学知识的本质是相近的,笔者执教苏教版五年级上册第二单元“多边形面积的复习”一课,对平行四边形、三角形、梯形等平面图形的面积计算进行回顾梳理.同为图形面积的复习,中美课堂教学方式有何不同呢?
“多边形面积的复习”主要由三个板块构成:回顾梳理——面积公式的推导;简单应用——图形面积的计算;深化学习——实际问题的解决.学习,不仅要知其然,更要知其所以然.本课伊始,学生在小组合作中,通过画一画、剪一剪、拼一拼,回顾面积公式如何得来,整个过程不仅是对知识的梳理,学生深思熟虑后的流畅表达也有助于形成系统的知识结构.“关于图形的面积计算,我们需要注意哪些?”这个问题将静态知识引向动态生成,学生根据公式计算已知底和高的平行四边形、三角形和梯形的面积,有了明确的指向,在计算中更加注重条件、单位等细节.“分别画一个平行四边形、三角形和梯形,使它们都与图中长方形的面积相等”,学习资源的整合,将单一的学习过程转变为问题情境的体验过程.通过自主探究,有的学生想到根据已知长方形的面积以及面积相等来推算平行四边形、三角形和梯形的底和高,也有学生联系之前所学,使所有图形的高都与长方形的宽一样,再根据图形面积公式的关联算出底的长度,充分交流、分享,促进知识的进一步重组.“已知上底、下底长度之和及高,求梯形田地面积”“刷正反面的平行四边形广告牌”“在长方形纸上剪直角三角形小旗”……在一系列生活中常见问题的探究中,学生正亲自体验“做中学”.这堂课侧重知识的关联性,为高阶思维的培养奠定了基础,在一次次挑战中,学生向着深度思辨逐步行进.
George老师的这堂课,结构简洁明了,课堂流程没有冗杂花哨,以设计小镇为主线,以一系列问题为引导,小镇平面图随着课的进行渐渐清晰.“上节课建造的小镇对建筑的周长提出了特殊要求.而这一课我们还要来造一个小镇,不过这一次将要用到面积的相关知识.”George老师首先营造了一种轻松、民主、多元化的课堂氛围,所呈现的图片和情境多为学生熟悉的场景——“我们如此热爱校园,首先请大家设计一个面积是24平方厘米的长方形学校平面图.”对学校的爱是一种自然沉淀的情怀,George老师将学生的情感培养无形地渗透于学科教学.又如,在要求学生画出一个周长为15.7厘米的圆形健身房平面图前,George老师出示不久前学生在冬运会上齐心拔河的情境.在教学过程中,他更多地站在一个引导者、倾听者的角度.“小镇的博物馆由一个正方形和两个半圆组成,正方形的边长相当于圆的直径,长度为4厘米.”这里他设计了三问:“想一想:博物馆的形状可能是什么样的?”学生在画的过程中发现了多种可能,George老师座位间巡视,对学生出现的问题耐心指导.“根据平面图,你能设法求出图形面积吗?”学生在图中标出数据,在讨论中回顾圆和正方形的面积如何计算.“求博物馆的面积,你有不同的算法吗?”因为两个半圆的直径与正方形的边长相等,求总面积,学生想出了不同的方法.George老师这节课呈现了多个开放性问题,课末,他还让学生在空白处自己设计一个建筑的平面图,求出总面积.最后,学生可以走下座位互相交流自己的小镇平面图,遇到问题时询问老师.在其乐融融的互动中,学生不断尝试,体验挫折,教师借助课堂巡视,及时进行个别交流,给予学生适时的指导和帮助.George老师不断整理学生的疑点和兴趣点,在充分的交流中学生的思维插上了想象的翅膀.
三、思辨:论民主点化生情,质疑声中有启迪
张奠宙教授在《小学数学教材中的大道理》一书中写道:“时代在进步,教育要面向世界、面向未来、面向现代化.”中外教师合作共研,给彼此的教学带来更多新的思考.从学生的课后反馈看,两位教师不同的教学方法给了学生不一样的启迪.尽管两堂课在内容、授课方式上各有特色,但都充分体现了问题解决的引导、知识构建的过程,以及数学思维的提升,对学生创新素养的培养具有一定示范和借鉴意义.
学生创新素养的培养依托宽松、民主又充满个性化的课堂环境,课上要鼓励学生去发现、提问.良好的数学课堂氛围能够促使学生积极主动地参与思考,激发他们的创造意愿.给学生越多的自由空间,他们就越能在教师的循循善诱下,经过自身的探究和同伴间的互帮互助理解知识,感悟数学思维方法,最终收获丰富的数学活动经验.在学生有创造性思考时,更应该加以肯定,尊重学生的想法.当然,探究的问题需要“跳一跳”才能摘得,即问题要能激起学生挑战、探索的欲望,他们在独立思考、积极探究中,将体会到数学学习的无穷魅力.比如,笔者在教学“钉子板上的多边形”时,通过发现问题、操作探究、表达交流等一系列数学活动,引导学生共同归纳出“求钉子板上多边形的面积可以用边上的钉子数n除以2,再加上内部钉子数a,然后减1”.这时,有学生迫不及待地问:“那多边形内没有钉子,这个方法还管用吗?”这时,不妨缓一缓,鼓励学生:“这个问题提得很好,多边形内部没有钉子是比较特殊的情况,老师也没有试过.同學们,我们一起来举例算一算吧!”学生最终在数学探究活动中,发现本课探索的规律同样适用于“a=0”的情况.
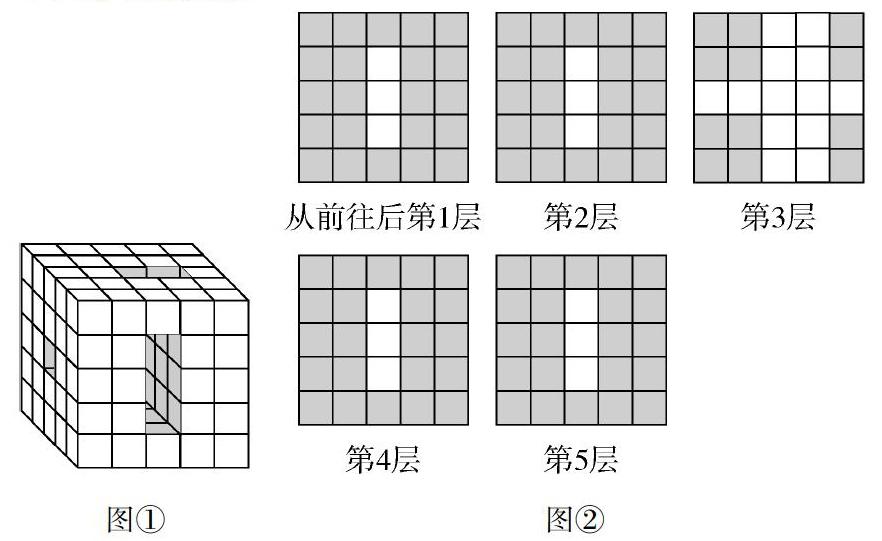
再如,学生探究问题“一个5×5×5的立方体,在一个方向上开有1×1×5的孔,在第二个方向上开有2×1×5的孔,在第三个方向上开有3×1×5的孔,求剩余部分的体积(如图①所示)”时,通过引导,部分学生能想到:先算出正方体的总个数,是5×5×5=125(个);接着,算出开3×1×5的孔所去掉的正方体个数,即3×5×1=15(个),再求开1×1×5的孔时所去掉的正方体个数,即1×1×5-1=4(个)(有1个正方体在前一次开孔时已被去掉),然后计算开2×1×5的孔时所去掉的正方体个数,即2×1×5-4=6(个)(有4个正方体在前两次开孔时已被去掉);最后,125-15-4-6=100(个).这样的方法能完全理解并运用的同学并不多,而想出这个方法的同学更是寥寥无几.因此,笔者激励学生:“这样的方法需要一定的空间想象能力,否则很难想明白.那你们再想一想:有没有更好的方法,让大家一下就能看清呢?”学生在小组中进行了激烈的讨论,最终有小组想到“我们以前学过画图的策略,这里也可以画图来解答”.师:“这里不是已经给我们画好图了吗?”学生解释:“我说的是平面图,根据观察和想象,我们可以把这个图从前往后分成5个板块,分别找出每个板块正方体的个数,最后相加,不就能算出总个数了吗?”笔者对学生的方法进行了肯定,并和学生一起回顾以前研究不规则平面图形的面积时,其实就用过两种方法“割”和“补”,这道题前一种思路是“补”,而同学们想到的这种方法就相当于“割”.学生对这样的方法进行了尝试(如图②所示),发现前两层和后两层都是一样的个数,只需要考虑从一个方向上挖去的个数,即5×5-3=22(个);中间一层稍复杂,需要考虑从三个方向挖去的个数,即5×5-13=12(个).最后相加,也能得到100个.后来,还有学生想到,也可以从左往右或者从上往下进行分层.这样的解答确实比原先的方法要清晰、直观、简单.在课堂上,笔者引导学生自主发现,联系新旧知识帮助学生理解,鼓励学生尝试探索,目的不再是单纯的解题,而是真正将教师的主导作用与学生的主体作用相统一,锻炼学生的思考力、想象力,培养学生勇于探索的精神.
图① 图②
教学中,为学生营造良好的学习环境,巧妙地运用探索式学习模式锻炼学生的思考能力至关重要.当教学过程偏离了原先的设定,当学生产生了新的思考时,所有的“意料之外”恰是创新的源泉,教师的激励、鼓励、肯定,课堂的民主、和谐、快乐,将激发学生继续探索的欲望,产生积极的学习效果,也让新的课堂生成变得别样精彩.创新意识的培养,需要每一位教师用智慧串起课堂中的每一个环节.在教与育中点化生情,是遇到难题时出奇制胜的关键.在学与习中鼓励质疑,那么这份异想天开将给学生的未来增添一抹不凡的色彩.
【参考文献】
[1]卢凤华.高校校园招聘会的优点、问题与对策[J].莆田学院报,2011(4):40-43.
[2]于盈.基于项目管理的高校校园招聘体系设计[D][硕士学位论文].北京:北京邮电大学,2010.

