圆背景下的线段最值问题

江苏省张家港市第二中学 王 伟

学生们要清楚地知道线段的最值问题是求线段长度的最大值或者最小值、线段和或差的最大值或者最小值。这些问题在学生的学习过程中出现的频率很高。在学生学习圆这一章节后，线段最值问题又以不同的面貌出现了。实际上就是灵活利用圆的定义和性质把新面貌下的线段最值问题转化成学生熟悉的线段最值问题，比如两点之间线段最短、垂线段最短、三角形两边之和（ 或差） 大于（ 或小于） 第三边等。教师在实际的教学过程中要不断地灌输解题策略，促进学生们的解题能力产生质的飞跃。

一、利用切线性质，转化为垂线段最短

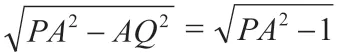
点拨：此题主要考查了圆的切线的性质、勾股定理以及垂线段最短的模型。遇到圆的切线，常连接圆心和切点，利用垂直构造直角三角形，根据勾股定理将线段的最值转化成垂线段最短的模型来解决问题。因此要求学生能根据题意，结合圆的切线性质去突破。

二、找到隐圆，利用最短距离模型

此前，学生已经掌握了“圆外一点到圆上的点的最短距离模型”，其中：最短距离就是“圆外的点和圆心的距离减去圆的半径”。但是，找到隐藏的圆对学生来讲很难，这就要利用圆的定义去找到圆。

例 2：如图3，四边形ABCD 是边长为1 的正方形，动点E、F分别从点C，D 出发，以相同速度分别沿CB，DC 运动（点E 到达C 时，两点同时停止运动）。连接AE，BF 交于点P，过点P 分别作PM ∥CD，PN ∥BC，则线段MN 的长度的最小值为_______。

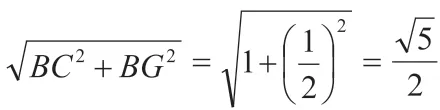
点拨：本题利用了“直角三角形斜边上的中线等于斜边的一半”、由圆的定义确定了圆、“圆外一点到圆上的点的最短距离模型”、勾股定理求解。利用圆的定义找到动点的运动轨迹是圆为解题的关键，将线段的最小值转化为“圆外一点到圆上的点的最短距离模型”解决。

三、利用轴对称，求线段和的最小值

在初中数学中，我们研究的主要图形是三角形、四边形、圆。纵观中考题，有一类题目就是利用轴对称性质构建线段和的最短路径模型，而圆恰好也具有轴对称性，所以也可以利用圆的轴对称性进行命题。

解析：如图6，作点A 关于MN 的对称点A'，连接A'B，交MN 于点P，连接OA'，OA，OB，PA，AA'。因为点A 是半圆上的三等分点，所以∠AON=60°。由圆的轴对称性可得：PA=PA'，∠AON=∠A'ON=60°。又因为点B 是劣弧AN 的中点，所以∠BON=30°，则∠A'OB=90°。因为OB=OA'= ，所以A'B=2，从而PA+PB=PA'+PB=A'B=2。

点拨：本题是要在MN 上找一点P，使PA+PB 的值最小。这是路径最短问题，解题的关键是利用轴对称性找到对称点。圆具有轴对称性，直径所在的直线是圆的对称轴。

通过上述例题的讲解，学生们应该知道了圆背景下的线段最值问题需要利用圆的定义及各种性质进行解题。当然，题型不仅仅有这三种，但是我们可以通过这三道例题知道，解题时要关注题意，利用圆的定义和性质，将新问题转化为见过的线段最值模型，从而顺利解决问题。同时，教师也需要不断去摸索，总结出经验，及时穿插到教学中，把正确的解题思路分享给学生。而学生们要想掌握圆背景下的线段最值问题的常用方法，就需要不断地练习，找寻到问题的关键所在才能解决根本问题，才能突破自己，收到事半功倍的效果。