一种针对直接入轨飞行器的主动段轨道快速实现方案
王 鹏,李 强,王 智,宋剑爽,宁 雷
(北京宇航系统工程研究所,北京 100076)
0 引言
轨道设计作为飞行器发射中一项重要的技术保障,直接关系到飞行器的发射准备时间和性能指标,进而影响到执行任务的能力。考虑性能指标的主动段轨道设计属于带过程约束的终端时刻自由、终端状态受约束的非线性最优控制问题,早期多采用间接法将最优控制问题转化为边值问题,进而通过数值方法求解,随着计算机水平的提高,目前多采用直接法求解,在不考虑时间指标的情况下均取得了较好的使用效果[1]。
为提升飞行器射前快速反应能力,希望在保证一定性能指标的情况下尽可能缩短轨道计算时间。诸多学者针对此问题进行了相关研究,当前主流的方法是通过离线计算或全局优化算法获得合理的参数初值,以此为基础采用序列二次规划等梯度数值算法求解[2]。考虑到相关方法对于优化指标并没有放松,因此仍属于最优化问题,所耗费的时间仍然比较长。
本文以直接入轨飞行器为研究对象,在不考虑地球旋转的情况下通过优化算法求解得到具有优化指标的轨道设计结果,在旋转椭球模型下基于球面三角确定射向,以此为基础考虑旋转影响对地球不转情况下的设计结果进行修正得到次优化的轨道结果。由于优化过程可以在射前离线进行,且射前仅通过参数修正即可得到当前射向对应的轨道设计参数,省去了射前的轨道迭代计算过程,因此发射准备时间大大缩短,有效地提升了射前快速反应能力。
1 问题描述
1.1 动力学方程
忽略内部介质相对于飞行器流动所引起的附加科氏力,假设在控制系统作用下飞行器始终处于力矩瞬时平衡状态,忽略控制力的影响,惯性坐标系中以矢量描述的质心动力学方程为
(1)
式中,P为推力矢量,R为气动力矢量,mg为引力矢量。设动参考系相对于惯性坐标系以角速度ωe转动,由矢量导数法可知
(2)
将式(1)代入式(2),可得动参考系中的质心运动学方程[3]
(3)
将上述各项投影到发射坐标系中即可得到发射坐标系中的动力学方程。
1.2 设计变量选取
直接入轨飞行器主动段轨道设计与传统轨道飞行器相似,可采用相同的飞行程序角模型,如图1所示。
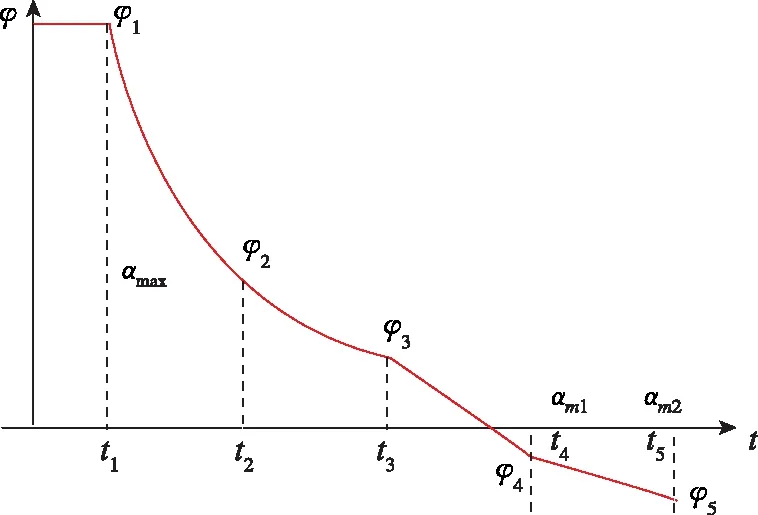
图1 主动段飞行程序角Fig.1 Boost phase flight program angle
即垂直起飞后不久开始在稠密大气层内以αmax实行负攻角转弯,在飞行速度接近跨声速段之前,将攻角收缩为零,在重力作用下继续转弯,直到满足分离条件φ3,为提高飞行器的稳定性,在发动机启动、关机以及级间分离前后,要求飞行器尽量减小飞行攻角,分离后通过末级飞行段设计攻角αm1和αm2进行能量管理以满足交班点约束条件。据此,飞行程序角模型可取为
φ=φ(αmax,φ3,αm1,αm2)
(4)
式中,φ为俯仰程序角,因[t2,t3]段重力转弯无设计变量,而在无动力滑行时,φ3和t3取一个即可,这里将φ3作为设计变量。同时,由于地球形状不规则以及自转影响,主动段轨道还与发射点地理纬度B0、高度h0和发射方位角A0有关,其中发射点是已知的,发射方位角可根据规划要求计算得到。
1.3 约束条件
主动段约束条件包括:
1)飞行最大动压约束:
Q≤Qmax
(5)
2)级间分离起控条件:
(6)
3)终端交班点高度和当地轨道倾角约束:
|hf-hfstd|≤Δhf,|Θf|≤ΔΘf
(7)
其中,Qmax为飞行最大动压约束;下标fl表示分离点参数,hflmin为级间分离最低高度,Qflmax为级间分离最大动压;下标f表示终端参数,Δhf为终端高度偏差,ΔΘf为终端当地轨道倾角约束。
1.4 优化指标
优化指标为终端的速度最大,即
J=-Vf
(8)
2 轨道优化设计与实现
在主动段满足飞行约束助推至交班点后,考虑到直接入轨飞行器自身可在入轨后大范围机动飞行,因此交班点的条件并非像传统卫星轨道要求那样严苛,在交班点高度和当地弹道倾角适当放宽的情况下,可转化为满足约束要求的可行区域。交班点条件的放宽带来了主动段轨道实现的新思路,即在不考虑地球自转、轨道设计与射向无关的情况下进行轨道相关参数的优化设计,实际使用过程中基于射向和发射点参数对轨道设计参数进行一定的修正,以降低交班点参数的偏差,最终满足交班点的约束条件。
2.1 不考虑地球旋转的设计参数优化
本文研究的内容为若干个设计变量情况下满足约束条件的参数优化问题,优化算法可选用序列二次规划算法(SQP),在离线优化过程中参数初值可通过经验法选取。
SQP算法的基本思想是在给定的近似点处通过二次近似逐渐得到一个更好的迭代点,这需要通过求解二次规划子问题得到,在当前迭代点处算法通过求解一系列的二次规划子问题,使得迭代点逐步接近原优化命题的最优点,算法最终收敛到最优解[4]。
设f,g,h分别为目标函数、等式约束和不等式约束且均二次连续可微,非线性规划问题(P)可表示为
(9)
对于问题(P),SQP方法通过序列地求解一系列的二次规划子问题来逐步逼近原问题的最优解,在迭代点xk处,与上式相对应的二次规划子问题(QP)可表示为
(10)
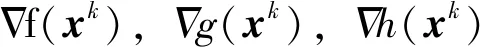
为实现SQP算法,还须解决两个问题[5],其一是矩阵Bk的修正,其二是QP子问题相容性。
在不考虑地球旋转的情况下,轨道优化设计过程中无须考虑发射点经纬度和射向的影响,由此可优化得到给定发射点高度下的轨道设计结果,作为考虑旋转椭球模型下设计参数修正的输入。
2.2 考虑地球旋转的设计参数修正
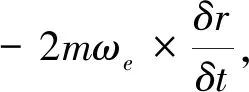
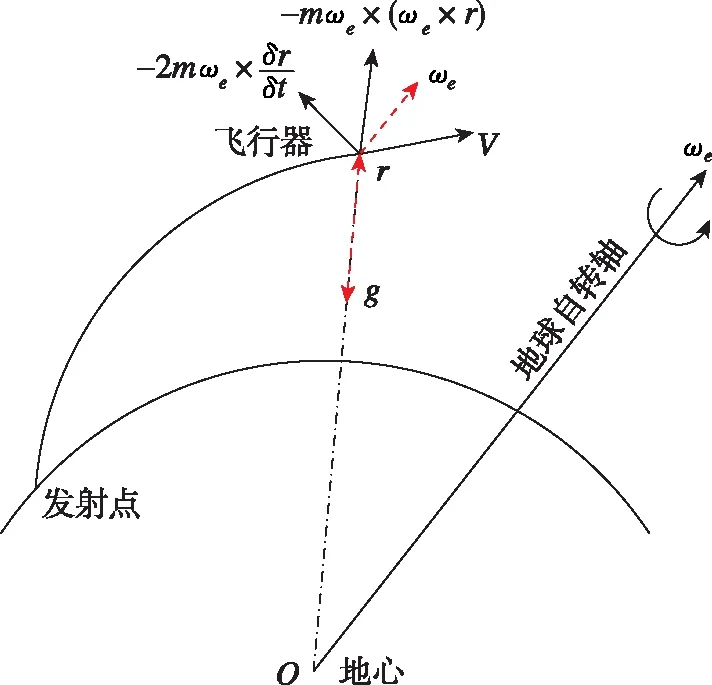
图2 飞行过程中的受力情况Fig.2 The force of flight process
对于直接入轨飞行器而言,相关的控制指令主要是俯仰程序角,在不考虑三通道参数相互影响的情况下,对俯仰程序角和飞行过程中的力对轨道的影响进行定性分析:
1)在同一套发射惯性系俯仰角φT(t)控制参数下,进行发射系俯仰角变化分析:
① 当A0∈(0°,180°),即射向向东时,任意时刻的φ(t)>φT(t);
② 当A0∈(180°,360°),即射向向西时,任意时刻的φ(t)<φT(t);
③ 当A0=0°或180°,即射向北或向南时,任意时刻的φ(t)=φT(t)。
2)在同一套发射系俯仰角φ(t)控制参数下,进行受力分析。考虑到在接近交班点过程中,速度方向逐渐接近当地水平线,此时:
① 当V向东时,科氏惯性力方向向上,等效于减小引力加速度的作用,交班点高度偏高;
② 当V向西时,科氏惯性力方向向下,等效于增加引力加速度的作用,交班点高度偏低;
③ 当V向北或南时,科氏惯性力为0,交班点高度保持不变。
由上述分析可知,对于同一套发惯系俯仰角φT(t),受地球旋转的影响,不但实际的控制指令由φT(t)变为φ(t),而且即使对于同一套φ(t),受附加力的影响,轨道的终端高度也会发生变化。
上述两方面影响中,程序角可以进行人为修正,由φ(t)=φT(t)-ωe(-cosB0sinA0)t可知,令
φ′T(t)=φT(t)+ωe(-cosB0sinA0)t
(11)
即可消除程序角指令变化带来的影响,其中φ′T(t)为修正后的发射惯性系俯仰角。
受力关系虽然不可补偿,但注意到上述程序角指令变化和产生的附加力对终端高度的影响都是同向的,例如当向东发射时,任意时刻φ(t)>φT(t)本身已经使得终端高度变高,而科氏惯性力的影响则使得终端的高度变得更高,因此可通过进一步修正程序角参数来“补偿”地球自转引起的附加力作用下的轨道偏差。
综上所述,修正项可选为K·ωe(-cosB0sinA0)t,则修正后的发射惯性系系程序角为
φ′T(t)=φT(t)+Kωe(-cosB0sinA0)t(K>1)
(12)
考虑到上述修正项中已经包含了时间t,可消除时间增长对后续轨道的影响,因此K一般取常值即可。
2.3 主动段轨道实现方案
考虑发射点高度的影响,通过在不考虑地球旋转的情况下进行轨道优化设计得到相关设计结果,将程序角参数考虑地球旋转影响进行修正,则可得到适用于旋转椭球下的程序角参数,由此可形成主动段轨道实现方案:
1)在地球不转情况下,考虑发射点高度区间,按高度间隔分别使用SQP优化算法计算得到发射点高度对应的程序角变化参数,最终形成以发射点高度为自变量的一维程序角数组;
2)基于实际的发射点高度插值程序角数组得到此高度对应的地球不转情况下的程序角参数;
3)考虑直接入轨飞行器机动飞行要求,根据交班点经纬度信息,采用球面三角理论确定发射方位角;
4)考虑地球旋转影响,基于发射方位角和发射点纬度,对程序角参数进行修正,得到最终程序角参数。整个主动段轨道实现方案的执行流程如图3所示。
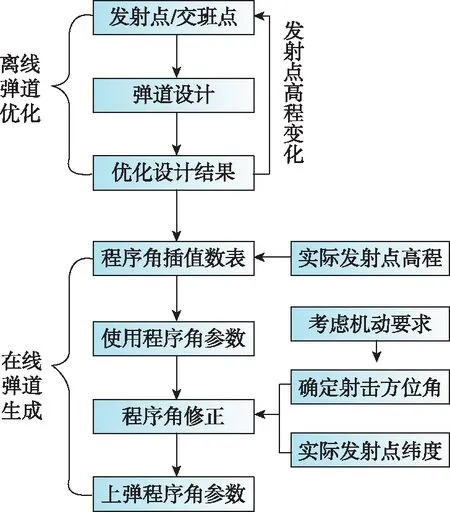
图3 主动段轨道实现方案Fig.3 Trajectory implementation of boost phase
3 仿真算例与分析
为验证上述轨道实现方案的有效性和可行性,基于地球不转模型,在发射点经纬度均为0,初始高度为h0、发射点高度间隔取h1的情况下,利用优化算法分别得到满足交班点参数要求的不同发射点高度情况下随相对发射点高度变化的发惯系俯仰角程序角插值数组,见图4。交班点参数要求包括终端高度和终端当地弹道倾角两个要求:其中终端当地弹道倾角要求为0°;关于终端高度,优化过程中要求严格等于标准值,而在程序角修正后的终端高度容许在标准值的基础上存在3 km的高度偏差。在上述基础上,交班点的速度越大越好。
基于上述程序角插值数组,已知发射点高度参数,可插值获取当前高度下不考虑地球旋转的程序角参数,采用上述程序角修正方案对相关程序角进行修正即可得到当前高度下考虑地球旋转的实际程序角参数。
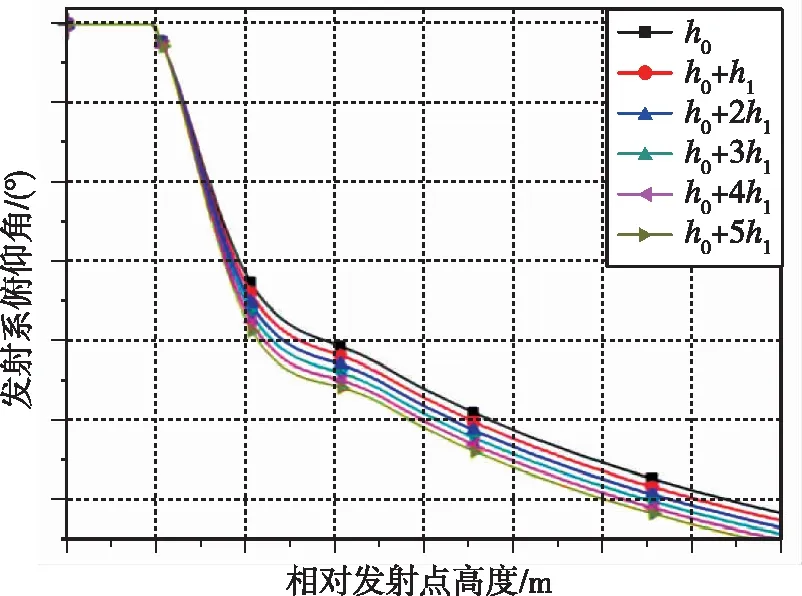
图4 发惯系俯仰角随相对发射点高度变化曲线Fig.4 Relationship between flight program angle and height
3.1 计算时间对比
在Windows XP操作系统上,采用主频≥2.6 GHz的I5处理器、容量≥4 GB的DDR2/3内存,基于C语言编写的计算程序,在同一发射点和交班状态参数下,采用程序角迭代计算和本文所使用的程序角插值后修正分别计算一条轨道所需的最长时间,对比结果如表1所示。

表1 计算时间对比
根据上述对比可知,采用程序角插值修正的方式由于没有迭代计算过程,大大缩短了计算量,使得计算一条轨道所需的时间显著减少,能够实现快速计算的要求。
3.2 交班点偏差分布对比
采用模拟打靶方式对国内纬度[18°,53°]和高度[0 m,3 000 m]范围内任意发射点、任意射向情况下进行轨道计算,计算过程中未考虑制导修正,以最高点作为终止计算条件,直接使用地球不转情况下的程序角和修正后的程序角分别计算得到的交班点高度偏差和速度偏差分布见图5和图6,相对标准值的标准差计算结果见表2,其中标准值是指不考虑地球旋转情况下通过优化得到的满足交班点约束的数值。
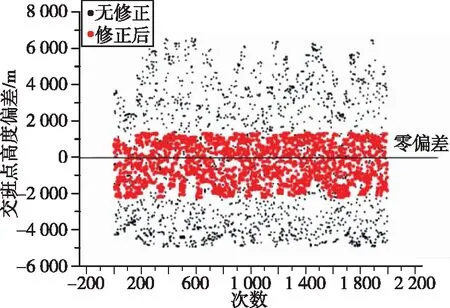
图5 交班点高度偏差散布图Fig.5 Intersection height scatter
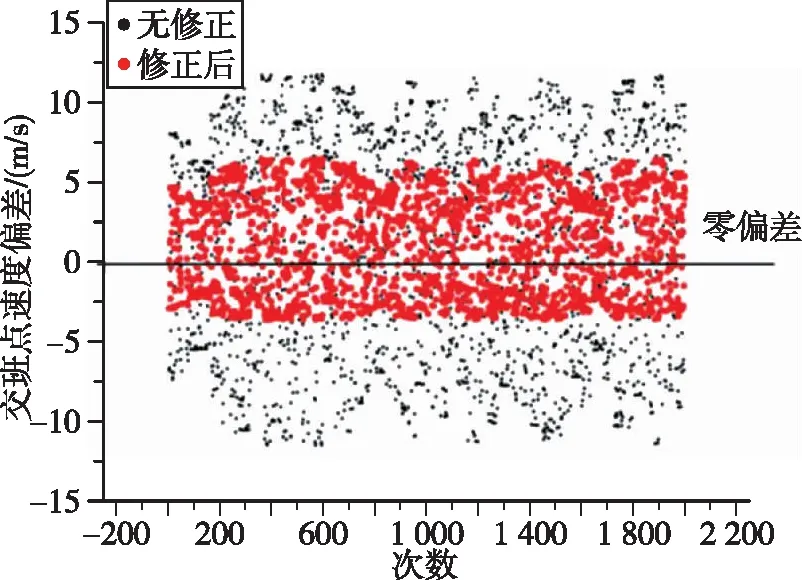
图6 交班点速度偏差散布图Fig.6 Intersection speed scatter
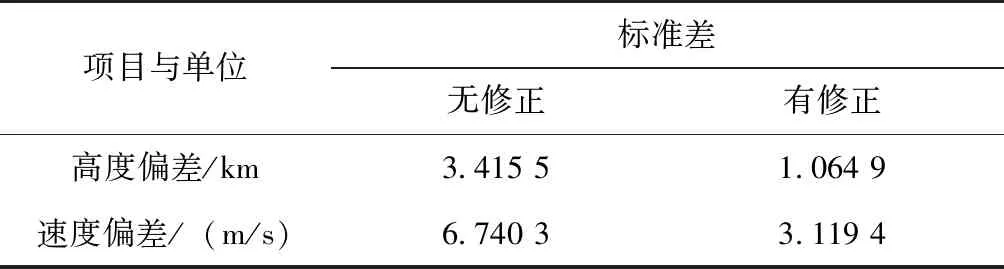
表2 标准差结果
由以上结果可得,相对不考虑地球旋转情况下的标准值,受点位和射向影响考虑地球旋转情况下速度和高度都会在标准值附近出现散布,但使用修正后的程序角参数可显著降低地球旋转因素的影响,最终交班点的高度和速度偏差大幅降低,在满足交班点要求的同时为后续飞行创造良好的初始条件。
3.3 优化指标情况对比
为验证修正程序角后轨道计算结果的优化指标情况,选取h0高度下的程序角参数,采用前述方法修正程序角,计算发射方位角A0∈[0,360)范围内的交班点参数。同时以此发射点参数和发射方位角作为初始条件,考虑过程约束和终端交班点约束,基于优化算法计算同样发射方位角范围下的交班点参数,两者高度偏差和速度偏差的对比结果见图7和图8。
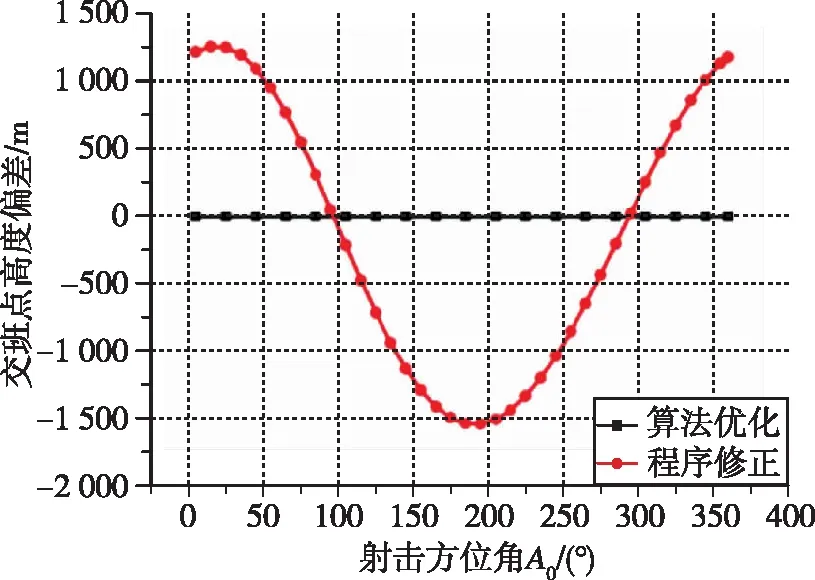
图7 交班点高度偏差随发射方位角变化情况Fig.7 Relationship between intersection height and launching direction
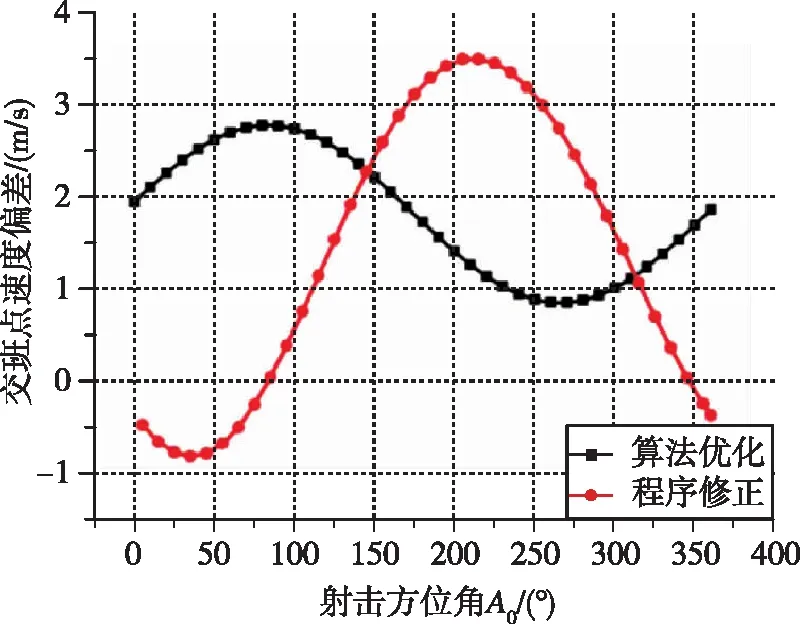
图8 交班点速度偏差随发射方位角变化情况Fig.8 Relationship between intersection speed and launching direction
由图7、图8可以看到,采用SQP算法优化可以精确满足终端高度约束条件,因此不随发射方位角变化,而终端速度受地球自转影响随发射方位角先增大后减小。对于采用程序修正的结果,终端高度和速度受能量守恒约束呈现此消彼长的规律,在不考虑终端高度差异的情况下,较优化结果使用程序角修正的最大速度偏小2.5 m/s左右,若考虑高度差异,则两者的速度差异将更小。由此说明,采用程序角修正的轨道实现方法仍具有一定的优化指标。
4 结论
本文研究了一种针对直接入轨飞行器的主动段轨道实现方案,采用地球不转模型计算指定高度下的程序角参数,使用时根据发射点高度插值得到对应的程序角,基于发射点纬度和射向对此程序角进行修正后作为考虑地球旋转模型的实际程序角。仿真结果表明,该方法仅需进行离线轨道优化,无需进行实时迭代计算,大大缩短了轨道实现所需的准备时间,同时所计算出的交班点参数偏差较小,能够满足交班点要求且具有一定的优化指标,具有一定的工程参考价值。

