空中发射运载火箭弹道优化设计

李庆龙，郑亚茹，徐 明

(北京航空航天大学宇航学院，北京 100191)

0 引言

空中发射是指由载机将运载火箭带到空中某一高度后进行发射。相比于地面发射方式，空中发射运载火箭有如下优势：1) 发射场地不受限制，全球任意位置都可发射；2) 入轨倾角无约束，发射场地的自由选择使得空中发射运载火箭可以发射任意倾角的载荷；3) 发射准备时间短，对地面基础设施依赖小，发射快速、灵活；4) 有效载荷比更高，由于空中发射带来的高度、速度及火箭气动升力的优势，相同总质量的火箭，空中发射运载火箭拥有更大的有效载荷[1]。鉴于以上原因，空中发射运载火箭受到广泛关注，美、俄等国对空中发射技术进行过大量的研究与工程实践，代表性的有美国“飞马座”(Pegasus)火箭、“空射号”(Airlaunch)火箭以及俄罗斯“飞行号”火箭[2]。目前投入商业运营的只有“飞马座”火箭，成功率高(发射42次，成功40次)。

空射运载火箭与传统地面发射运载火箭的区别是：1) 空中发射运载火箭携带机翼，提供较大气动升力；2) 空中发射运载火箭水平投放发射。空射运载火箭的这些优势也导致了其弹道设计的复杂性，形成多约束、多变量的非线性优化问题。针对弹道设计中多约束、多目标的特点，多种优化方法被有效应用于弹道设计中，其中既包括传统的共轭梯度算法、动态规划法、SQP法等方法，也包括遗传算法(GA)、蚁群优化算法、粒子群算法(PSO)等智能优化算法[3-7]。智能优化算法具有全局最优的特点，但是其收敛速度慢、精度较低，而传统非线性优化算法具有收敛速度快、局部寻优能力强的特点，但对优化变量初值的依赖性较强，一般需要预先根据经验或理论公式提供合理的设计变量初始值，而当前问题动力学公式复杂，无法提供近似解析解，同时约束复杂，依赖经验给出初值极难。因此，本文以飞马座空中发射运载火箭为研究对象，建立其质心动力学模型及气动力计算模型，以此为基础，设计了有翼空射火箭水平投放发射方式的弹道分级优化方法，即以遗传算法全局寻优筛选合适的设计变量初值，再运用起作用集法和内点法在该初值附近寻优，从而快速获得满足飞行约束的具有最大有效载荷的弹道参数，并以“飞马座”火箭数据为参照，验证了该分级优化算法的可行性。

1 空中发射运载火箭的动力学模型

1.1 空中发射运载火箭的质心动力学模型

建立发射坐标系下的火箭质心运动方程

mar=P+A+mg-mae-mac

(1)

式中，ar为火箭的质心加速度，P为发动机推力，A为气动力，g为引力加速度，ae为牵连加速度，ac为科式加速度。在控制系统理想无惯性的假设下，忽略发动机以外的因素对推力和质量流量的影响，可进一步得到式(1)在发射坐标系下的投影形式

(2)

式中，Llb为箭体坐标系到发射坐标系的转换矩阵，Lba为气流坐标系到箭体坐标系的转换矩阵，{g}l和{ωe}l分别为引力加速度和地球自转角速度在发射坐标系下的投影。运载火箭质心动力学模型中涉及的其他定义及参数见参考文献[8]。

1.2 空中发射运载火箭的气动力模型

如引言所述，就运载能力而言，空中发射运载火箭利用了两方面的优势：

1)载机平台提供的发射初始速度(Ma=0.82)以及高度优势(海拔11 000 m)；

2)运载火箭一级的翼型提供额外的气动升力，可以快速抬升高度。

因此，建立合理的空射运载火箭气动力模型是必要的。本文基于飞马座火箭翼型(如图1所示)，建立空中发射运载火箭的气动力计算模型。

图1 飞马座运载火箭气动外形[1]Fig.1 Aerodynamic configuration of the Pegasus rocket[1]

基于运载火箭气流坐标系建立气动力模型

(3)

式中，ρ为当地大气密度，v为飞行器速度，Cl为升力系数，Cd为阻力系数，S为飞行器外露翼的面积，α为飞行器攻角；Cl-α，Cd均为速度(马赫数Ma)的函数，文中参考了文献[9]中飞马座的气动实验数据。

1.3 空中发射运载火箭的飞行控制模型

对于弹道优化设计而言，选取合理的设计变量来描述优化问题是关键点。因此，作为分级优化方法的补充，需要根据空中发射运载火箭的飞行特点，建立恰当的飞行控制模型，准确描述整个飞行过程，支撑后续弹道优化设计。空中发射运载火箭一般由飞机载至指定空域，达到预定高度和速度后水平投放。投放后为保证飞机的飞行安全，需使用空气舵进行姿态控制，保持要求姿态飞行一定时间。此后一级发动机点火，火箭迅速拉起，利用发动机推力和气动升力爬高，在一级发动机熄火前已基本飞出稠密大气层。一级发动机熄火后,火箭一、二级分离，二级发动机点火，继续爬高加速，飞出大气层后抛掉卫星整流罩。由于固体发动机燃烧时间短，火箭二级熄火时一般达不到卫星要求的轨道高度，因此需要在二级熄火后安排一个无动力滑行段，让火箭爬至要求高度，接着三级发动机点火，将卫星加速至预定速度，送入预定轨道[10]。

因此，将空中发射运载火箭俯仰程序角φ(t)分为：1)大攻角爬升段；2)大攻角保持段；3)降低攻角；4)小攻角平飞段；5)改平攻角；6)零攻角飞行段；7)真空第一段；8)滑行段；9)真空第二段，共9段进行设计[11]。

其中，一级发动机工作段由1)～6)组成，具体来讲，该段飞行轨道一般分为4段：①飞机投放后姿态保持段:此段火箭保持要求姿态飞行，以保证投放后飞行安全，此段火箭飞行时间约5 s；②发动机点火后大攻角爬升段，此段火箭飞行速度还不太大，可采用较大攻角α1爬升，以迅速爬高，减少后面飞行中火箭所受到的空气阻力；③保持升力飞行段，此段火箭已获得一定飞行速度和高度，可保持一定攻角α2，调整至最佳升阻比飞行，继续爬高和加速；④零攻角飞行段，此段火箭已获得较大的飞行速度和高度，发动机接近熄火，为改善火箭一、二级分离的条件，火箭保持零攻角飞行[10]。该阶段攻角变化规律如图2所示，其数学表达式如式(4)所述。

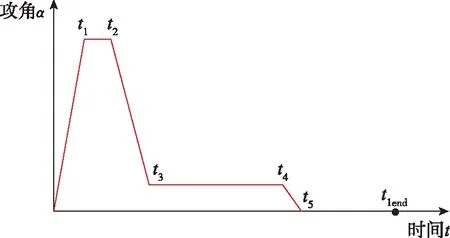
图2 一级飞行段攻角变化规律Fig.2 Change of angle of attack of the first stage

(4)

火箭的俯仰程序角满足

φ(t)=

(5)

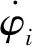
2 空中发射运载火箭的弹道优化设计

空中发射运载火箭弹道优化问题的数学描述为

(6)

式中，x=[x1,x2,…,xn]T为优化设计问题的设计变量；gi(x)为约束条件；f(x)为优化设计问题的目标函数。以下针对此一体化设计问题中不同要素进行具体说明。

2.1 目标函数

一般而言，运载火箭在优化设计过程中，主要有如下性能指标要求：1)主动段结束时位置、速度；2)最大有效载荷；3) 最小成本；4)最小起飞总质量。当确定火箭型号后，其起飞总质量范围已限定；此时，对于给定目标轨道的发射任务，设计具有最大有效载荷的弹道可以提高收益比。因此，对于空中发射运载火箭的弹道优化问题，目标函数设定为：给定火箭型号，即确定火箭起飞推重比范围、发动机型号与目标轨道的情形下，使得入轨时的有效载荷最大。

2.2 约束条件

此问题中的约束条件共有6个，同时包括不等式约束和等式约束，分别是：1)最大飞行动压qopt≤qmax；2)最大轴向过载overloadopt≤overloadmax；3)大攻角爬行段的最大攻角；4)入轨点位置火箭的轨道高度hopt=hset；5)入轨点位置火箭的弹道倾角θopt=θset；6)入轨点位置密切轨道的轨道倾角iopt=iset。

2.3 设计变量

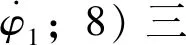
3 空中发射运载火箭的弹道优化设计方法及仿真校验

3.1 弹道优化设计方法及流程

空中发射运载火箭弹道优化问题属于多设计变量、多约束的非线性优化问题，同时目标函数的解析表达式形式较为复杂。而传统的非线性全局优化算法，如起作用集法、内点法等具有局部收敛速度快、精度高的优势，但对优化初值依赖性较强，需要预先找到较为准确的可行解，否则易陷入局部最优或是无法求解；而智能优化算法，如遗传算法可以实现全局寻优，但是由于遗传算法生物进化的搜索策略，其计算过程耗时长，求解精度粗糙。针对以上特点，制定了同时包含遗传算法(GA)、起作用集算法(ASM)和内点法的分级优化流程。其中，通过遗传算法全局寻优，筛选优化问题初始设计变量，继而利用起作用集算法和内点法获取初始优化变量的局部区域内的最优解，最终得到满足飞行过程约束和入轨条件的有效载荷最大的弹道。分级优化流程如图3所示,在单次迭代求解过程中，设置前后两次迭代最大有效载荷之差作为结果是否最优的判断准则；同时，对每种优化方法设置最大迭代次数上限，若超出此限制，使用下一种优化算法求解。此外，当内点法未能取得最优解但比起作用集法结果更优时，以本次优化结果作为起作用集法初始设计变量，再次寻优，即实现起作用集法和内点法的交叉寻优，获得更好的优化结果。

(a) 分级优化设计流程

(b) 单次迭代弹道求解流程图3 空中发射运载火箭弹道优化设计流程Fig.3 The optimization design flow of air-launched rocket

3.2 仿真校验

根据文中描述的空中发射运载火箭弹道优化设计模型，以“飞马座”(Pegasus)火箭为蓝本进行优化。Pegasus火箭基本参数见表1和表2。发射任务的目标轨道为高度600 km，轨道倾角为45°的近圆轨道，轨道的升交点赤经和近地点幅角由发射时间确定，发射时间选择为2019年9月1日4时(UT)，投放位置高度11 km，纬度40°，投放速度Ma=0.82，采用滑行入轨方式，目标轨道参数见表3。优化过程中，首先使用遗传算法对弹道可行解全局寻优，获得精度较差的全局最优解，以遗传算法求得的最优设计变量作为起作用集法和内点法的设计变量初值，进行二次局部寻优，从而获得满足入轨精度要求的弹道最优解。

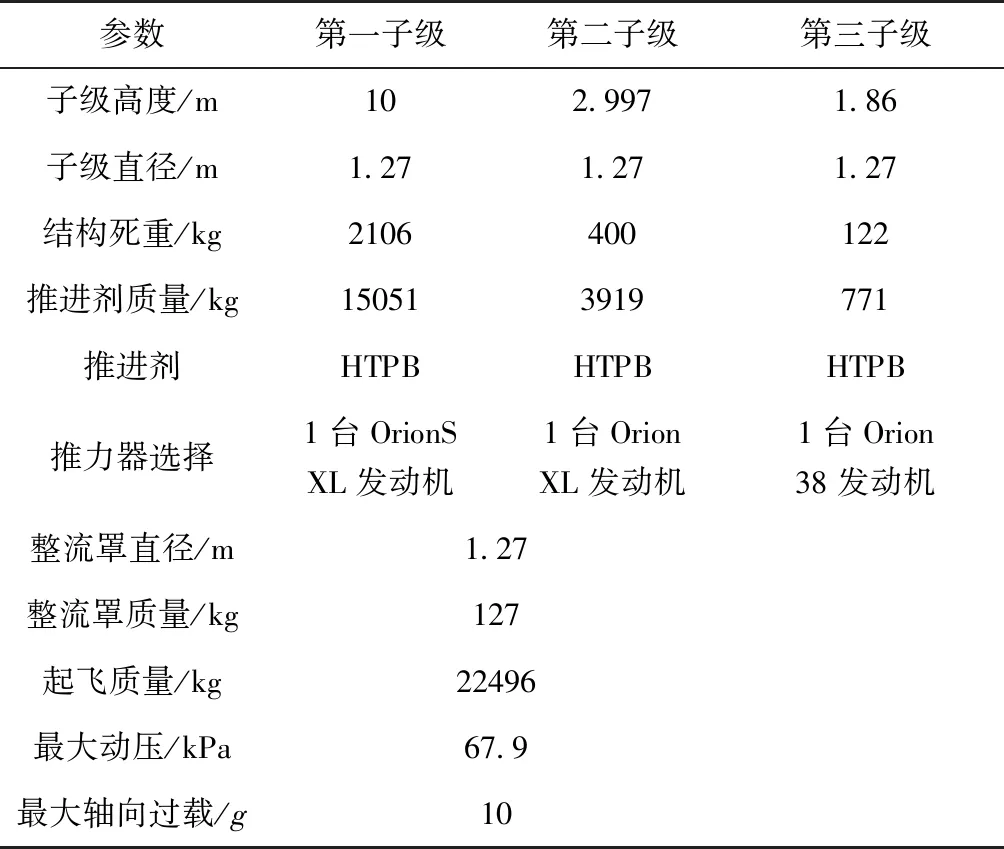
表1 Pegasus运载火箭基本参数

表2 Pegasus火箭发动机参数

定义入轨精度tol表达式

(7)

式中，a为实际入轨的半长轴，a0为目标轨道半长轴；i为实际入轨的轨道倾角，i0为目标轨道倾角；e为实际入轨的轨道偏心率，e0为目标轨道偏心率。

求解结果表明，遗传算法全局寻优得到的弹道入轨参数如表3所示，入轨精度tolga为0.4193，入轨半长轴误差约为1 km，而轨道偏心率相差0.4191，需要对此弹道再次寻优，使用起作用集方法和内点法二次寻优后，入轨精度达到tol=3.131×10-9，满足入轨精度要求。此外，遗传算法计算耗时约为40 min，而起作用集法和内点法总耗时约为38 s。以上结果验证了使用遗传算法、起作用集法和内点法的分级优化策略可以有效提高弹道求解的精度和速度。空中发射火箭弹道曲线及最优弹弹道参数见图4、表4。

表3 轨道参数

表4 最优弹道参数

由图4高度曲线(a)和速度曲线(b)可知，采用滑行入轨方式的空中发射运载火箭弹道曲线符合航天器飞行的一般规律，入轨精度3.0131×10-9，符合入轨要求。由图4动压曲线(c)和轴向过载曲线(d)可知，在飞行过程中，最大动压38.96 kPa，满足设计最大动压67.9 kPa的约束，最大轴向过载9.94g，满足飞行过程约束。由图4(g)攻角曲线可知，火箭以最大攻角17.89°快速爬升16 s后，以5.89°攻角的最佳升阻比形式飞行31 s，随后保持零攻角飞行，最大限度地利用了空射火箭翼面提供的升力。由图4(e)弹道倾角曲线和(f)俯仰程序角曲线可知，火箭滑行结束时，弹道为负倾角;此时，实际轨道为椭圆形，为了进入最终圆轨道，按照图4(f)所示俯仰角线性控制策略圆化轨道，抬升弹道倾角，最终获得符合入轨要求的弹道。

(a)飞行高度曲线

(b)速度曲线

(c)动压曲线

(d)轴向过载曲线

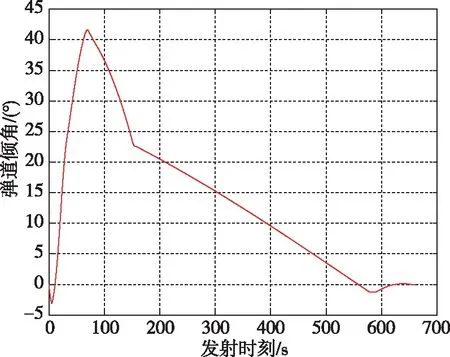
(e)弹道倾角曲线

(f)俯仰程序角曲线

(g)攻角曲线图4 空中发射运载火箭弹道曲线Fig.4 Time history of ballistic of air-launched rocket

图5为在以遗传算法给出的最优弹道参数作为起作用集法/内点法设计变量初值的迭代寻优过程，图中每个点均为满足入轨约束及飞行过程约束的可行解，经过20次迭代寻优，最优解即最大有效载荷质量稳定在317 kg附近，获得给定空射火箭及入轨条件下的最大有效载荷对应的弹道参数。

图6给出了从北纬40°发射的空射运载火箭对不同轨道高度的圆轨道运载能力。图7分别给出了在赤道附近(北纬8°)对15°倾角以及中纬度发射位置(北纬40°)对大倾角椭圆轨道空中发射运载火箭的运载能力，其中，椭圆轨道近地点均为180 km。结果表明，本文给出的分级优化方法适应性强，可优化的目标轨道范围广阔，具备对任意倾角、任意发射位置、中低圆轨道或椭圆轨道(包括太阳同步轨道)的弹道优化设计能力。

图5 起作用集/内点法迭代寻优过程Fig.5 The optimization process of the active-set method/interior-point method

图6 LEO轨道和SSO轨道运载能力 (发射点纬度：北纬40°)Fig.6 The capacity to LEO and SSO (Latitude of launch point: 40°N)

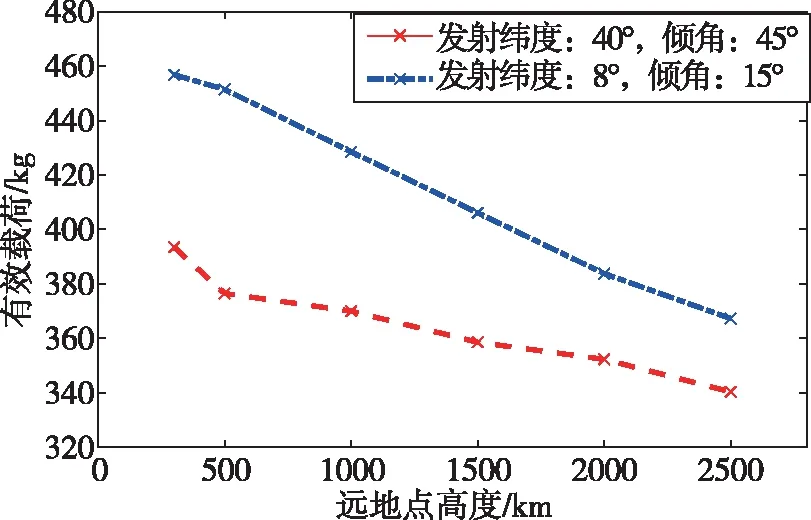
图7 椭圆轨道运载能力(近地点高度180 km)Fig.7 The capacity to elliptical orbit (The altitude of perigee: 180 km)

4 结论

针对空中发射运载火箭的弹道设计问题，本文给出了详细的空中发射运载火箭的动力学模型及弹道控制模型，并建立了基于遗传算法全局筛选初值，起作用集方法和内点法二次局部寻优的分级优化方法，该方法优化求解速度快，适用性强，具备任意发射位置、任意倾角的圆轨道及椭圆轨道的弹道设计能力，能够最大程度地挖掘空中发射运载火箭的运载能力，为空中发射运载火箭弹道优化设计提供数据支持。同时，基于“飞马座”空中发射运载火箭的仿真实例验证了本文提出的弹道优化设计模型及分级优化算法的合理性与准确性。