火箭协同优化中的气动代理模型研究

沈 丹, 彭 博, 李舟阳, 宫宇昆, 李平岐

(北京宇航系统工程研究所，北京 100076)

0 引言

随着运载火箭研发模式的转变，快速迭代和协同优化设计成为主要发展方向。特别是在总体小回路论证时,涉及弹道、气动和姿控等专业，需要从大量构型中筛选可行方案，气动计算对整个方案的设计有较大影响，为实现快速论证,需要气动特性计算实现在线输出数据。而当前运载火箭的气动特性主要依靠风洞试验和CFD仿真计算得到，需要耗费较多的资源和时间周期，无法满足快速论证和优化的需求，亟需研究一种快速计算运载火箭气动特性的方法，这一过程对精度要求相对较低，但对速度要求相对较高。

在CFD方法出现之前，运载火箭的气动设计主要依靠工程算法。然而，工程算法基于无黏、有势、小扰动等假设，因此对使用范围有严格的限制。一般不单独使用某种公式来给出气动特性数据，需要多种公式和修正手段复合求解，这些复合的方法打包形成软件，例如著名的美国空军DATCOM软件包，在有翼导弹快速设计中发挥着重要作用。然而，DATCOM软件中没有适用于捆绑助推器的复杂外形经验算法[1-2]，因此无法引入到大型运载火箭的协同优化当中。

求解线化位流PG方程的面元法，只需要对飞行器表面进行网格划分，建模复杂度较小，由于面元法求解的是线性方程组，因此其计算速度很快。当前较成熟和通用的面元法代码是NASA为波音公司开发的PANAIR[3]。但由于线化位势方程框架本身的假设，它不可处理跨声速情况，也不适合用于处理黏性效应和气流分离显著的情况，因此不适宜引入到大型运载火箭的协同优化当中。

近年来，随着多学科优化( Multidisciplinary Design Optimization，MDO)和气动外形优化(Aerodynamic Shape Optimization,ASO)的发展，选择近似的数学模型，将气动特性对外形参数的响应看成黑箱问题，采用样本结果对黑箱问题进行训练和辨识，进行气动特性分析的方法被广泛采用，形成了多种类型的代理模型[4]。本文针对运载火箭外形变化的特点，对气动参数拟合的代理模型进行研究。

1 代理模型构建途径

代理模型通过对若干采样样本(不同的火箭外形)气动计算数据进行多次分析，得到对部分或全部设计空间的模拟，从而得到气动隐式函数模型的显式函数近似表达式，其流程如图1所示，主要步骤为：

1) 确定设计变量x1,x2,…,xm，确定设计空间(设计变量的上下限)。对于运载火箭气动计算，设计变量是标准火箭外形的一系列拓扑类型和尺寸参数，设计空间为总体设计对火箭外形的约束范围；

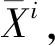
3) 本文针对气动计算外形需要进行前处理操作，即生成几何模型并划分空间网格；

4) 利用数值试验的方法确定在样本点xi处的系统响应值yi，并利用它们构成一系列样本对{(xi,yi),i=1,2,…,m}，其中yi=(y1,y2,…,yq)，是一个q维响应值，针对火箭气动特性，yi指升力系数、阻力系数、压心系数等期望得到的计算结果；

5) 选取一部分样本对做为训练样本，采用适当的近似方法构建代理模型，确定代理模型f(xi)的参数，使f(xi)与yi近似程度最好，剩余样本用做检验模型精度。如模型预测精度满足设计要求则结束，否则修改模型参数或者增加样本，直到其预测精度满足要求为止。

图1 代理模型的构建途径Fig.1 Construction approach of surrogate model

2 设计空间

大型运载火箭一般采取捆绑助推器的构型，我国现役和在研的运载火箭往往采用2个或4个助推器，本文示例的是四助推器的构型，如图2所示。图中的参数和尺寸充分且唯一地定义了火箭的气动外形。按照经验将头部锥角和捆绑缝隙宽度固定为常值，其余16个设计变量变化取值，构成不同的火箭外形。因此本文中的设计空间是16维的高维空间。

RF-整流罩球头半径；L1-头部第一锥长度(到实际尖点)；A1-头部第一锥锥角；L2-头部第二锥长度；A2-头部第二锥锥角； LF-头部直筒段长度；DF-直径；L3-头部倒锥长度；LC1-芯级直筒一长度；DC1-直径；L4-芯级过渡段长度； LC2-芯级直筒二长度；DC2-直径；RZ-助推球头半径；LZ-助推顶点/全箭顶点距离；LZ1-助推第一锥长度(到助推顶点)； AZ1-助推第一锥锥角；LZ2-助推柱段长度；DD-助推直径；H-芯助缝隙；BB-尾翼弦长图2 设计变量释义Fig.2 Definition of design variables

根据总体设计各专业经验，形成如下约束条件，最终形成设计空间：

1)芯级直径大于助推直径；

2)整流罩直径与相邻芯级直径比范围：1～1.6 ；

3)相邻芯级直径比例(芯级下段直径除以上段直径)：1～1.5 ；

4)助推器长度与全箭总长的比例：25%～65%。

3 试验设计

试验设计(Design of Experiments，DOE)为代理模型构建提供训练和测试样本，其合理与否关系到代理模型的预测精度，采样样本点要尽量充满整个空间，应该是整个设计空间的具有代表意义的典型子集，具有良好的均匀性和正交性。由于本文中的设计空间是16维的高维空间，采用拉丁超立方试验更为适宜。拉丁超立方试验设计是专门为仿真试验提出的一种试验设计类型。它是一种充满空间的设计，使输入组合相对均匀地填满整个试验区间，并且每个变量只水平使用一次。拉丁超立法试验设计具有非常好的空间填充能力，可以拟合非线性相应，即较正交试验设计而言，可以用同样的点数研究更多的数据组合[5]。

假设设计问题共有r个因子，每个因子分为n个间距，每个间距里面取一个值，则每个因子有n个水平值，拉丁方设计表是有r个因子的n个水平值组成的一个n×r矩阵，算法可用下式描述

(1)

其中，1≤j≤n,1≤j≤k，k是水平数，n是因子个数，U是区间 [0,1]上的随机数，π是序列0,1,…,k-1的一个排列。下标j是因子索引，上标 (i)是水平索引。抽样时首先将[0,1]区间划分成N个互不重叠的子区间，然后在每个子区间中进行独立的随机抽样。

4 样本生成

为避免样本生成耗费过长的周期，同时保持一定的工程应用精度，本文使用高精度无黏分析软件Cart3D对飞行器进行气动特性分析。该软件首先在全流场域生成各向尺寸一致的粗糙网格，再根据模型结构在物面附近自动逐步加密得到尺寸合适的流场网格，程序能通过定义网格区域及网格密度，自动捕捉模型的几何特征，快速生成笛卡尔网格(图3)，极大地压缩网格生成时间，最后求解Euler方程得到流场结果。该方法网格生成效率高，流场求解速度快，能大大缩短计算时间。为高效批量生成几何模型并划分网格，采用程序控制的脚本模式运行上述过程。

图3 样本生成中Cart3D计算网格Fig.3 Cart3D mesh

为验证Cart3D软件的计算精度，应用国内某型经典捆绑运载火箭标准外形使用Cart3D和Fluent软件分别开展计算并比较，结果如表1所示。针对标准外形，在各马赫数下Cart3D与Fluent的计算误差最大约13.4%(升力系数，Ma=3.0，攻角a=0°)，平均误差在10%以内，可以用于样本库的建立。

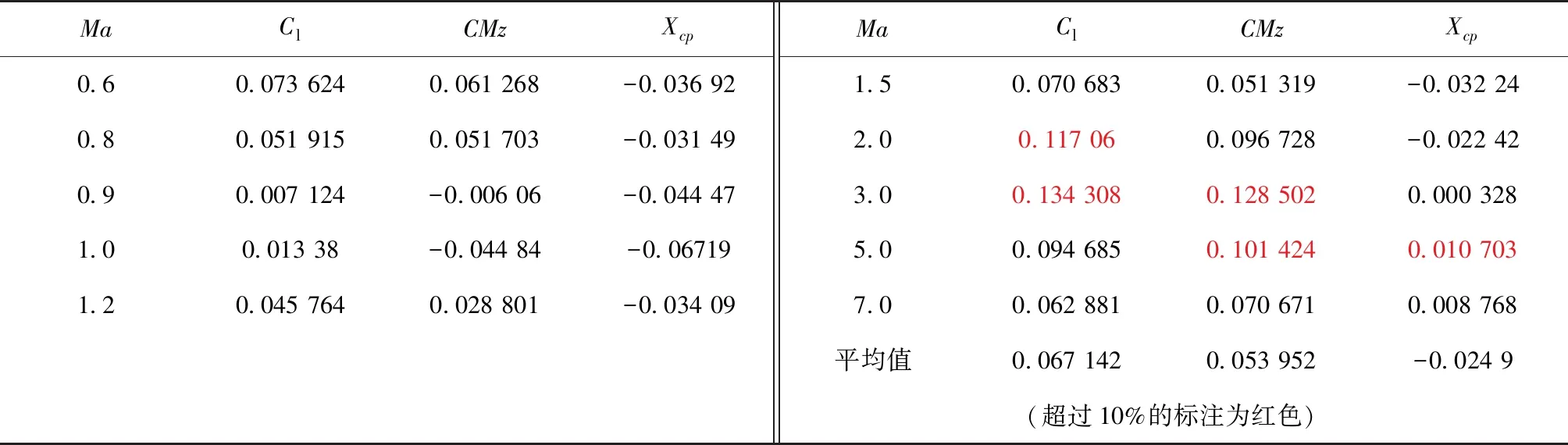
表1 Cart3D与Fluent结果相对误差

5 模型研究

常用的代理模型有：多项式响应面模型、径向基 RBF 插值模型、Kriging 模型、SVM支持向量机、BP 神经网络等，表2给出了上述几种近似模型及其优缺点[6]。由于本文研究的对象维度高、非线性较强，要求拟合方法的鲁棒性较强，因此选用了标准Kriging模型并使用GA遗传算法进行内参优化。同时选用BP神经网络(30×2)作为对比学习组，对Kriging结果进行对比评价。

表2 基本代理模型适用性比较

5.1 Kriging-GA模型

给定n个样本点S=[s(1)，s(2),…，s(n)]T，其中s(i)16维向量(火箭外形参数个数)，对应的目标函数值为Y=[y(1)，y(2),…，y(n)]T，其中y(i)是3维向量(升力系数、阻力系数、压心系数3个变量)。设计变量为x，对应的目标函数为y。

Kriging模型由全局模型和局部偏差模型构成[7-8]

y=F(β,x)+z(x)

(2)

z(x)的协方差矩阵表明其局部偏离的程度，形式如下

cov(z(ω),z(x))=E[z(ω)z(x)]=σ2R(θ,ω,x)

(3)

式中，R(θ,ω,x)是表示任意两个样本点xi,xj之间的相关函数，这里采用高斯相关函数

(4)

(5)

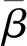
(6)

求解上式的非线性无约束优化问题，使用MATLAB工具中的遗传算法GA(Genetic Algorithm)对16维内参θk(k=1,2,…,k)进行全局寻优，从而得到最优插值的Kriging模型。Kriging模型可以在全局范围内提供对预估计值的误差评估，如式(7)所示。由此可以获得模型预测不确定性最大的位置[9]，并在该位置上添加新的样本点。

(7)

在设计空间中随机取2 000个外形参数，按上式计算全局偏差，如图4所示。将均方误差0.02作为红线，将红线之上的测试点进行标记，使用Cart3D计算并加入到样本库中。

图4 随机测试点的均方误差Fig.4 RSME of random test points

5.2 BPNN模型

BP 神经网络(Back Propagation neural network，BPNN)是众多神经网络算法中应用最为广泛的一种，在人工神经网络的应用中，80%～90%的人工神经网络模型都是采用 BP 网络或者它的变化形式[10]。对于火箭气动特性而言，诸参数具有高度非线性，因而拟合工具的非线性十分重要。本文采用两个隐含层的结构，每层含30个节点，如图5所示。

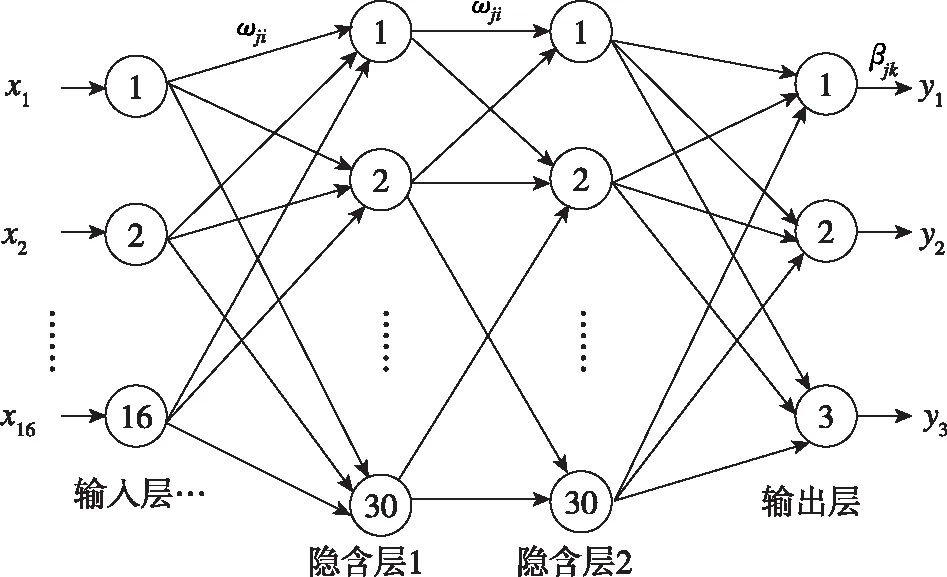
图5 BP网络拓扑结构图Fig.5 BP network topology

使用交叉验证方法[11]对样本点进行检验，例如针对四助推器在Ma=1.5，a=4°这一个工况的380个样本，每次取1个作为测试点，取剩余379个点作为训练点，可以得到图6中的误差分布规律，误差符合正态分布。但误差的分布范围很大，个别点的误差高达100%～400%以上(红色圈出)，使用其余样本点训练得到的网络在这些点上是无效的，由此可以推断这些样本点与其余样本点具有较大差异，如果数值试验结果可信，则需要在这些点周围增加样本。

图6 交叉验证误差分布Fig.6 Cross-validation error distribution

在加点位置围绕其中心，以原值50%为半径的超球面作为加点空间，使用均匀试验设计进行加点，对每个目标点周围以同种方式加12个“卫星点”，将样本点规模扩充为500个。对加点后的样本库再次进行交叉验证，误差分布如图7所示。由此可见，加点之后的误差分布更为集中，标准差减少34%，加点效果明显。

图7 加点后的交叉验证误差分布Fig.7 Cross-validation error distribution after adding points

5.3 结果分析

选取490个样本点作为训练组，按上述方法得到对于气动特性的估计即升力系数、阻力系数、压心系数(参考长度为样本的箭体长度，参考面积为1 m2)，选取另外10个作为评估组，则两种方法的拟合值与期望值相比较如图8所示，可以看出预测值较好地落在期望值上下两侧。

(a)升力系数

(b)阻力系数

(c)压心系数图8 评估点处的预测值Fig.8 Predicted value at evaluation points

根据式(8)对平均相对误差(MRE)的定义，Kriging-GA方法和BPNN方法得到的代理模型在评估点集得到的误差如表3所示，可以看出Kriging模型略优于BPNN模型。

(8)

6 结论

代理模型作为保证一定精度条件下对复杂数值模型的替代，在运载火箭总体协同优化中可发挥重要的作用。本文探索了火箭气动计算代理模型的完整过程，采用平均相对误差指标评估代理模型的预测精度，评估结果表明：

1)对于运载火箭外形变化引起气动特性变化这类问题，在16维变量、500个样本点规模的特定情况下，应用Kriging的误差小于BPNN；

2)利用Kriging模型作为代理模型的方法可满足工程需求，平均相对误差小于10%。