带预设性能的火箭垂直着陆段姿态自适应控制设计

李璟澜,杨秦敏

(浙江大学控制科学与工程学院, 杭州 310027)

0 引言

研制低成本、高可靠、高效率的运载器一直是航天界追求的目标[1]。实现运载火箭各子级的无损回收，从而通过重复使用来分摊运载火箭的发射成本，是可行的技术途径之一[2]。目前，SpaceX公司Falcon 9系列火箭的多次成功回收，也再次证明了垂直起降重复使用模式的可行性[3-4]。

垂直着陆段的姿态控制是可重复使用火箭的关键技术。考虑火箭子级返回过程中，其姿态角和角速度呈现复杂的非线性耦合特性，且存在气动参数偏差、严重环境干扰以及火箭自身燃料变化引起的重心和转动惯量变化等，经典控制方法往往难以保证控制系统的精度和稳定性。因此，需要设计更为先进的控制系统以满足火箭垂直返回段姿态跟踪的性能需求。

周军等[5]考虑弹性振动和液体晃动为外界干扰，采用鲁棒观测器设计了运载火箭的姿态控制系统。薛宇等[6]考虑参数不确定性和外部干扰，采用鲁棒控制理论设计火箭姿控系统，仿真结果表明，对参数不确定性具有良好的鲁棒性。赵党军等[7]将自抗扰控制思想与微分代数结合，提出了一种新的自抗扰姿态控制器方法，提高了运载火箭姿态控制系统的可靠性，但其使用的算法模型依然为标称轨迹下的小偏差线性化模型。此外，动态逆控制[8]、滑模控制[9]、神经网络控制[10]和鲁棒增益调度控制[11]等方法也被用于解决运载火箭姿态系统的稳定控制问题，但这些工作大多针对运载火箭发射、大推力入轨和在轨飞行阶段进行研究，较少分析运载火箭垂直着陆段的模型特性和性能需求。钱默抒等[12]针对运载火箭一子级垂直着陆前的姿态调整阶段，提出了一种基于滑模动态面控制技术的垂直回收控制策略，可实现姿态角的非线性跟踪控制。

本文将针对火箭一子级垂直着陆段的姿态控制问题展开研究，提出一种带预设性能的姿态自适应控制策略，能够有效地解决外界环境干扰、参数不确定性以及系统未知动态对系统的影响。该控制策略中，引入了误差转换技术，在对姿态角跟踪误差进行系统变换后设计自适应控制律，可满足用户预设的瞬态和稳态性能需求，进一步提高了运载火箭姿态控制系统的可靠性和控制精度。

本文内容安排如下：第一节建立了垂直着陆段火箭的姿态动力学模型；第二节引入了误差转换技术，基于神经网络和自适应方法设计了带预设性能的姿态自适应控制系统，并通过Lyapunov理论完成了对闭环系统的稳定性分析；第三节通过开展数值仿真实验，充分验证了本文提出的控制方法的有效性和强鲁棒性。

1 火箭姿态动力学模型

定义箭体坐标系为Oxyz，坐标原点O为火箭质心,z轴为箭体外壳对称轴，方向沿箭体轴指向火箭头部，与x，y轴构成右手直角坐标系。考虑运载火箭为刚性箭体，其姿态动力学方程可表示为

(1)

(2)

式中，sηsinη,cηcosη,tηtanη。τ∈R3为火箭栅格舵产生的控制力矩；M(T,δx,δy)为尾部发动机推力矢量作用下产生的箭体偏转力矩，在本文中假设偏转力矩与发动机推力大小T、发动机摆角δx和δy成函数关系；同时，火箭飞行过程中燃料消耗和贮箱液体晃动等因素将引起火箭箭体转动惯量的变化，记为ΔJ，其对应产生的摄动力矩可表示为MΔJ；Mext为气流速度引起的气动力矩，考虑飞行环境中普遍存在不可测的风速干扰，该气动力矩视作未知环境干扰。为方便表示，可定义dMΔJ+Mext为总未知干扰力矩。

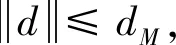
2 火箭姿态控制系统设计

2.1 控制目标描述

本文的目的在于设计一种带预设性能的自适应控制算法，在未知环境干扰和未建模系统动态同时存在的情况下，实现对火箭垂直着陆段飞行过程中期望姿态角ηd=[φd,θd,ψd]T的高精度跟踪；同时，为保证飞行安全，火箭姿态角将始终被限制在预设的运行范围内，表示为

(3)

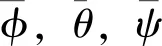
假设2期望姿态角轨迹ηd=[φd,θd,ψd]T和预设的姿态角上下界已知，均为关于时间连续可导的光滑函数。

2.2 误差转换

定义姿态角跟踪误差为

eη[eφ,eθ,eψ]T=η-ηd

(4)

结合式(3)可得到

(5)

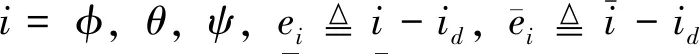
为实现预设的控制性能，本文引入误差转换技术将上述原始的受约束跟踪误差信号(约束误差信号需保持在预设的误差上下界内)转换为一个新的不受约束的误差信号。误差转换函数可表示为

(6)

式中，si∈R为转换后误差，Zi(·):R×R×R→R为用户自定义的随ei严格递增的光滑函数，即∂si/∂ei>0。同时，该函数满足

(7)

可以判断，若转化后的误差si有界，则原始误差ei有界，且始终维持在预设的误差域内。因此，上述控制目标转化为寻找合适的控制律，以保证误差信号si是有界的。

本文中，选取如下误差转换函数

(8)

式中，ln(·)为自然对数函数，Z0∈R+为正实数。

接下来，需要进一步获取经转换后新的误差动态。总写式(6)为

(9)

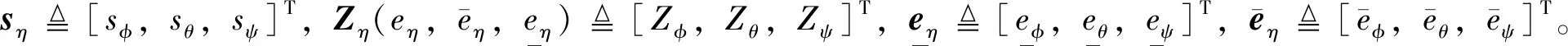
并进行如下定义

(10)

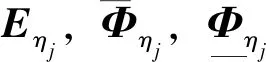
接着，对公式(9)中的姿态转换误差依次求时间微分可得到

(11)

式中

(12)

进一步对式(11)求时间微分有

(13)

式中

(14)

类似的，上述公式中Mη1和Mη2可通过计算得到。

接着，定义滤波跟踪误差为

(15)

式中，λη∈R+为正实数。

结合式(1)求解上述滤波跟踪误差rη的时间微分，可得到

(16)

2.3 神经网络补偿器

针对火箭姿态动力学(1)中的未知系统动态M(T,δx,δy)，本文引入一个三层的神经网络加以补偿。神经网络的输出可表示为

(17)

M(T,δx,δy)=W*Tφ(VTX)+ε

(18)

式中，W*∈Rn×3为输出层的理想权重矩阵，ε为对应的函数逼近误差。如果隐含层的权重随机初始化并且在随后的学习过程中保持不变，通过增加隐含层节点个数n，可使得逼近误差ε足够小。此外，考虑隐含层权重V在学习过程中保持不变，在下文的叙述中将予以省略。

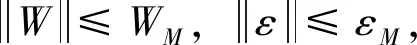
2.4 姿态控制器设计

本文针对运载火箭垂直着陆段飞行的自适应姿态控制器设计为

(19)

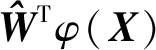
(20)

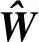
(21)

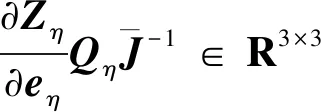
(22)

式中，μ∈R+为正实数。

本文所设计的姿态控制算法的稳定性由以下定理给出。

定理1考虑公式(1)所描述的运载火箭垂直着陆段姿态动力学模型，当假设1～3成立时,如果选择姿态控制器(19)，以及自适应律(20)和(22)，可以保证姿态角跟踪误差eη渐进趋于零点，且闭环系统其他信号始终有界。

证明：构造Lyapunov函数为

(23)

对V求时间微分可得到

(24)

将公式(16)和(18)代入式(24)有

(25)

接着，代入姿态控制器(19)，式(25)可写作

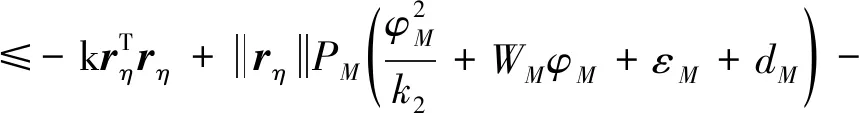
(26)

考虑下式始终成立

(27)

则公式(26)可计算为

(28)

进一步，将自适应律(22)代入式(28)，得到

(29)

对式(29)两边同时取时间积分有

(30)

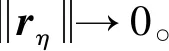
3 仿真验证

3.1 仿真参数设置

仿真中采用的运载火箭总体参数如表1所示。

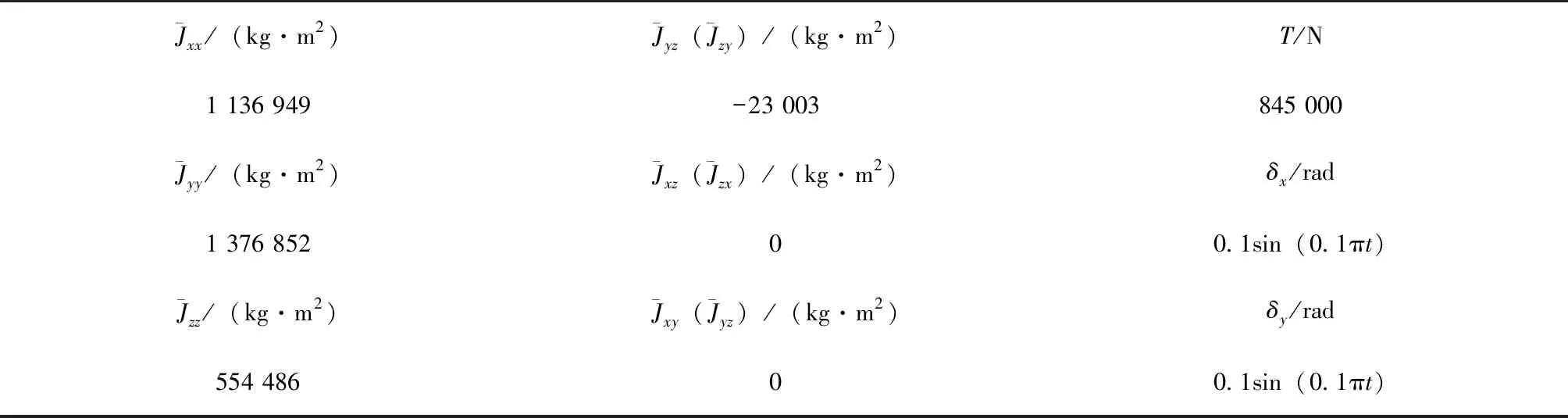
表1 仿真参数

垂直着陆段飞行的各初始姿态角选择如下

φ(0)=31.51°,θ(0)=20.05°,ψ(0)=2.86°ωx(0)=ωy(0)=ωz(0)=0(rad/s)

(31)

仿真中姿态控制器各控制参数选择为

k=200,k1=k2=λη=2,μ=300

(32)

待更新参数初始值设置为

(33)

未知气动干扰力矩在仿真中设定为

Mext=104×

[sin(0.1πt),sin(0.2πt),cos(0.1πt)]T(N·m)

(34)

垂直着陆段飞行中的惯性参数摄动为

(35)

尾部发动机推力矢量作用下产生的偏转力矩假定为

M(T,δx,δy)=

T[-sin(δx),sin(δy)cos(δx),0]T(N·m)

(36)

为充分验证所设计的姿态自适应控制算法的有效性，本文将给出上述外部干扰和未知系统动态均存在下的火箭垂直着陆段的姿态跟踪控制仿真。

3.2 仿真结果和分析

考虑未知气动干扰力矩Mext、发动机推力矢量带来的未知偏转力矩M(T,δx,δy)以及燃料消耗带来转动惯量变化ΔJ引起的干扰力矩同时存在于运载火箭垂直着陆段的飞行过程中。分别设计PD控制器和上文中自适应控制器，在给定参考姿态轨迹和预设控制性能下，各姿态角响应曲线如图1～图3所示。

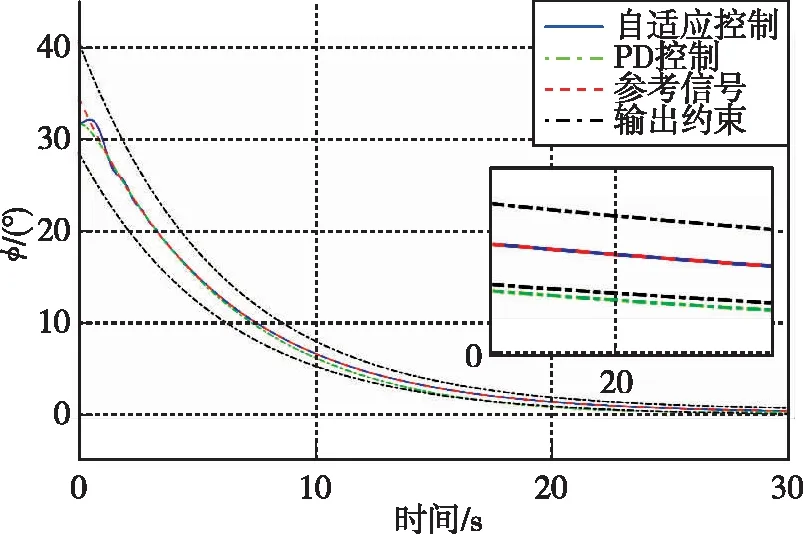
图1 时间-滚转角变化曲线Fig.1 Time history of roll angle

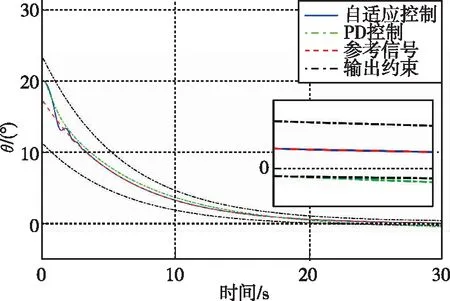
图2 时间-俯仰角变化曲线Fig.2 Time history of pitch angle

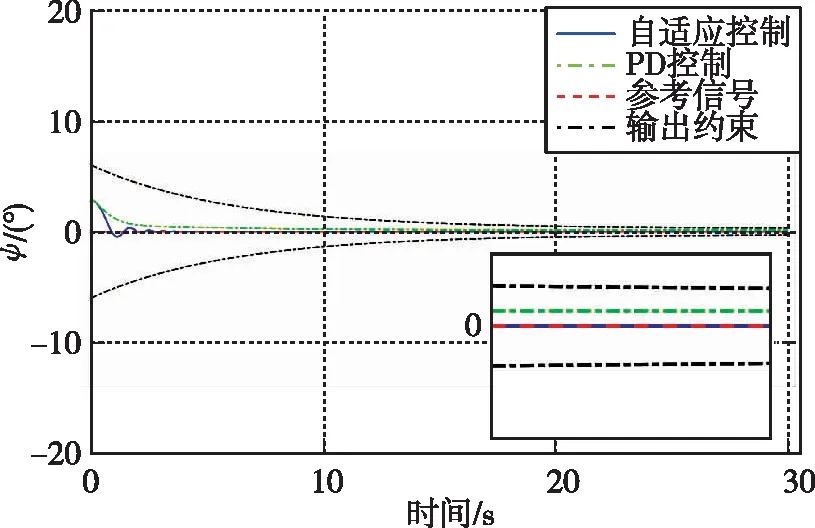
图3 时间-偏航角变化曲线Fig.3 Time history of yaw angle

由各姿态角随时间的响应曲线可知，在外部干扰、模型不确定性同时存在的情况下，相比于PD控制器，本文提出的自适应控制方法能在短时间内实现对预定姿态轨迹的稳定跟踪，具有更强的鲁棒性。同时，通过自定义姿态角跟踪误差的的上、下界，可使得姿态轨迹始终处于预设范围内，而PD控制器下则无法实现该性能。本文所设计的带预设性能的姿态控制器一方面可以用于改善火箭姿态控制系统的瞬态响应性能，另一方面可以保证其稳态性能。以本文的仿真算例为例，通过预设姿态角跟踪误差的上、下界函数，系统稳态误差将始终小于0.3°，这充分显示出本文设计的自适应姿态控制算法的高稳态精度。

4 结论

针对可重复使用运载火箭复杂非线性和强不确定性等动力学特性，基于自适应控制技术设计了火箭垂直着陆段飞行的姿态控制方法。同时，引入误差转换技术，实现用户预设的控制性能。研究表明，本文设计的带预设性能的自适应控制算法能实现对预定姿态轨迹的稳定跟踪，闭环系统具有良好的瞬态和稳态性能，且对外部干扰和模型不确定性具有强适应性。