基于Copula函数的华南台风灾情重现期研究*

王 萌，刘合香，卢耀健，李广桃

(南宁师范大学 数学与统计科学学院，广西 南宁 530001)

1 引 言

华南地区是中国遭受台风影响最严重、最频繁的地区之一[1].如2015年台风“彩虹”、2016年台风“莎莉嘉”和2017年台风“天鸽”的登陆，都对华南地区造成了严重的灾情影响.研究登陆华南地区的台风灾害有着比较重要的意义.

近年来，一些学者通过建立不同的模型对华南地区台风灾害展开了灾情研究.陈仕鸿(2011)等[2]根据广东省台风灾害历史数据，将选取的5个评估因子分为5个等级，建立了离散型Hopfield神经网络模型，对广东省的台风灾情进行评估.陈燕璇(2016)等[3]采用主成分分析(PCA)、等距特征映射(ISOMAP)和信息熵特征提取方法，将选取的致灾因子和承灾体因子作为输入，灾情等级作为输出，建立了登陆广西台风的灾情概率神经网络模型，对台风灾情进行预评估.

Copula函数常被应用于水文灾害研究中，为了更准确地研究自然灾害的重现期，一些学者通过建立Copula函数重现期模型来对自然灾害的灾情进行分析.万永静(2017)等[4]采用Copula函数，构建了不同重现期下的降雨量与潮位的二维联合分布函数，计算两者的遭遇频率.马建琴(2017)等[5]对提取的水文干旱特征变量，利用多种Copula函数模型拟合其联合分布函数，计算对应的联合重现期和同现重现期，对水文干旱的发生频率进行了分析.

借助Clayton Copula函数，构造灾情因子受灾人口、农作物受灾面积和直接经济损失的三维联合分布，计算华南台风灾害的灾情重现期，探讨台风灾害的发生频率，将会是有价值的研究工作.

2 理论与方法介绍

2.1 单变量边缘分布函数的选取及参数估计

利用Copula函数对选取的变量构造联合分布之前，需要确定各变量的边缘分布函数.选取一些常用的分布来构造边缘分布.这些分布分别为指数分布(Exp(λ))、伽马分布(Ga(α,λ))、正态分布(N(μ,σ2))、对数正态分布(LN(μ,σ2))和韦布尔分布(Weibull(a,b,c)).

使用矩法估计对单变量的不同边缘分布函数进行参数估计.采用矩法估计参数是因为它具有易于使用和不需要知道总体分布的优势.

选用Kolmogorov-Smirnov检验法(简称K-S)，对单变量的边缘分布函数进行拟合优度检验，选出最优的拟合分布函数.

2.2 Copula函数

2.2.1 Copula函数的定义

由Nelsen(2006)[6]可得到二维Copula函数的定义.

若函数C为二维Copula函数,在[0,1]2→[0,1]则满足：

(1)∀u,v∈[0,1],有C(u,0)=C(0,v)=0,C(u,1)=C(1,v)=v，

(2)∀[u1,u2]×[v1,v2]⊆[0,1]2,有C(u2,v2)-C(u2,v1)-C(u1,v2)+C(u1,v1)≥0.

其中u,v，u1,u2,v1,v2为分布函数.

设F是一个三维分布函数，它的边缘分布可用F1，F2，F3表示.存在一个三维Copula函数C，使得对任意的x1,x2,x3∈R都满足

F(x1,x2,x3)=C(F1(x1),F2(x2),F3(x3)).

(1)

其中C:[0,1]3→[0,1]，F1(x1),F2(x2),F3(x3)分别表示变量X1、X2和X3的分布函数.特别地，若F1，F2，F3是连续函数，则C是唯一确定的.

2.2.2 Copula函数的形式选取及参数估计

在Archimedean(阿基米德)型Copula函数中，Gumbel-Hougaard(简称GH)、Clayton和Frank Copula函数被广泛应用于水文以及自然灾害研究中[7].选取这三种Copula函数构建变量的联合分布函数.

对二维Copula函数进行参数估计时，采用的是相关性指标法[8].该方法需要先计算两变量的Kendall秩相关系数τ，再根据τ与Archimedean Copula函数的参数θ之间的关系式求解得到参数θ的值.

在估计三维Copula函数的参数时，选用极大似然法.它不仅克服了运算复杂的问题，而且还能取得较为优异的估计结果[9-10].根据式(1)求出其对应的三变量联合分布密度函数，构造三变量的似然函数，得到对数似然函数，计算对数似然函数的最大值点，即可得到三维联合分布函数中参数θ的最大似然估计值.

2.3 重现期

对于要计算的重现期是指研究灾情类似的台风灾害平均多少年重复出现一次.通过选取的台风灾情因子计算得到的重现期来衡量某类台风灾害发生的频率.其重现期可用T表示，常用的单位是 “年”.

其中，定义单个变量的重现期为

(2)

三变量联合重现期是指变量X1,X2或X3超过某个特定值的重现期，其计算公式为式(3).

(3)

三变量同现重现期是指变量X1,X2和X3都超过某个特定值的重现期，见式(4).

(4)

3 实例分析

3.1 数据来源及因子选取

为了描述台风灾害的灾情情况，从人口、建筑、农业和经济四个方面选取受灾人口、倒塌房屋数、农作物受灾面积和直接经济损失作为灾情因子进行分析[11].再从台风灾害数据的完整性考虑,选取的台风灾情数据来源于1981-1999年中国气象灾害大典[12-14](广东卷、海南卷、广西卷)、2000-2003年广东省、海南省和广西气候中心和2004-2014年中国热带气旋年鉴[15].2015-2016年灾情数据来源于广西气候中心、广东气候中心和海南气候中心，2017年灾情数据来源于中国气象灾害年鉴[16].

为了消除各灾情因子间的量纲影响，对其原始数据进行归一化处理.利用Spearman和Kendall秩相关系数法对灾情因子进行两两间检验.得出受灾人口、农作物受灾面积和直接经济损失两两因子间具有较强的相关性.从台风灾害的灾情因子间的强相关性及代表性考虑，选取台风灾害的受灾人口(X1)、农作物受灾面积(X2)和直接经济损失(X3)三个灾情因子来研究华南台风灾害.

3.2 单变量分布的最优选取及参数估计

针对选取的受灾人口(X1)、农作物受灾面积(X2)和直接经济损失(X3)，从常用的指数分布、伽马分布、正态分布、对数正态分布和韦布尔分布中，利用矩法估计变量的参数，结合K-S(Kolmogorov-Smirnov)检验法，分别选取这三个变量的最优边缘分布，其中三变量的具体分布情况见表1.

根据K-S检验的原则，其值越小说明该分布拟合的效果越好.从表1中可看出，受灾人口的K-S检验值最小为0.1918，其对应的分布为正态分布，说明受灾人口用正态分布拟合最优.农作物受灾面积在对数正态分布下的检验值最小，为0.1422，应该用对数正态分布拟合该变量的分布.直接经济损失拟合最优的分布为对数正态分布，经K-S值计算，该变量在对数正态分布下的检验值为0.1125，是最小值.

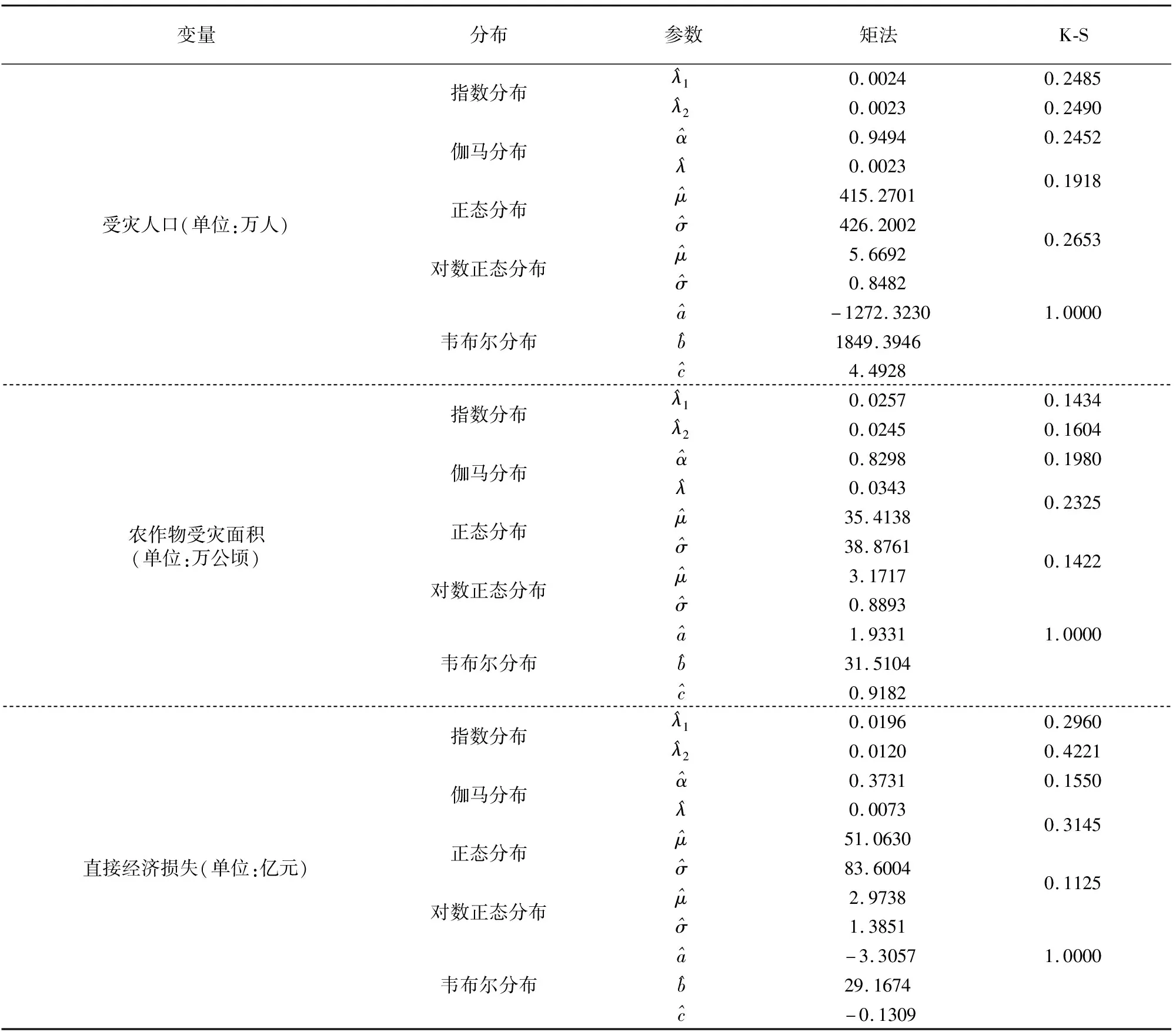
表1 不同分布的参数估计值及拟合优度检验

根据X1、X2和X3三变量的拟合分布函数，可绘出它们各自所服从的最优分布函数与对应的经验分布函数拟合曲线图进行对比分析，具体如图1-3所示.

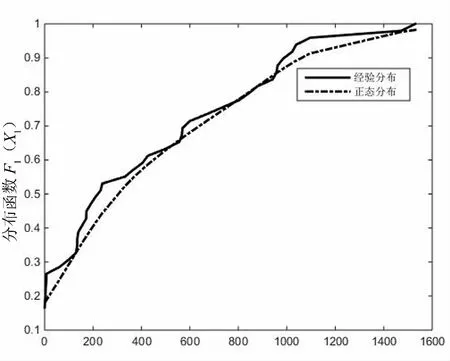
受灾人口X1/万人

从图1-图3中可以看出，随着单变量观测值的增加，对应的经验分布函数值逐渐接近于1.选取的最优分布的函数值也随着对应的单变量观测值的增大而越接近于1.

直接经济损失X3/亿元

从这3个变量的分布拟合图中还可以发现，这三个变量的经验分布函数曲线图与其对应的最优分布函数曲线图相比，两者的趋势基本一致，整体都大致呈逐步递增趋势.

从图1可看出受灾人口用正态分布拟合其经验分布，虽然拟合值与实际观测值相比偏小，但整体趋势一致，且误差较小，表明用正态分布拟合受灾人口这一变量较为合适.

从图2可以看出用对数正态分布拟合农作物受灾面积，与实际观测值的经验分布函数曲线大致重合，只有个别观测值存在误差，且误差值较小.根据两者分布函数曲线图的对比，可得农作物受灾面积这一变量用对数正态分布拟合较为合适.

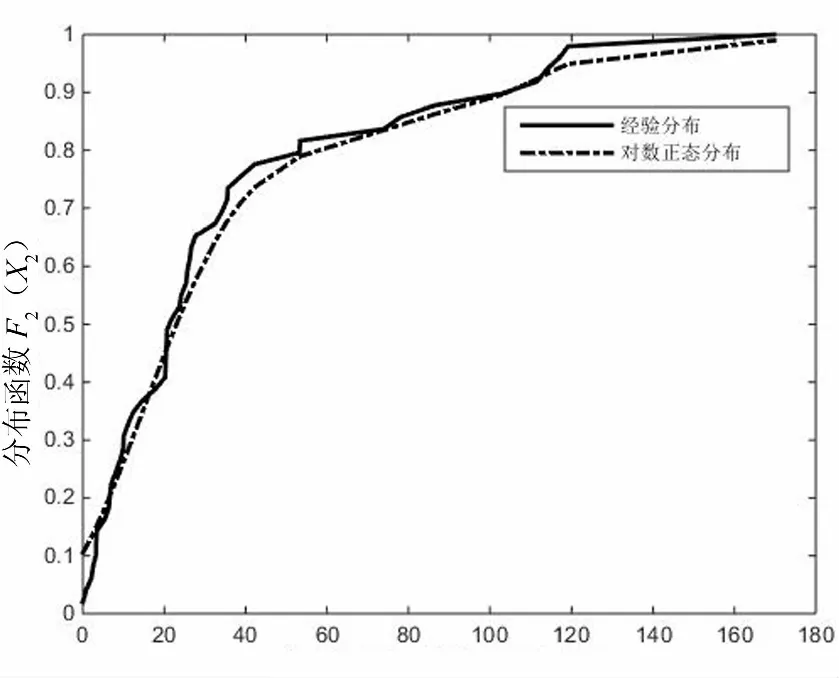
农作物受灾面积X2/万公顷

由图3可得，直接经济损失的经验分布函数图与对数正态分布函数图的曲线几乎完全重合，说明可以用对数正态分布拟合其分布.

3.3 二维Copula函数的参数估计及拟合优度检验

利用Spearman和Kendall秩相关性系数检验方法，对受灾人口(X1)、农作物受灾面积(X2)和直接经济损失(X3)两两变量间进行了相关性系数检验，具体结果见表2.

表2 变量间的相关系数表

由表2的计算结果可看出，不管是Spearman检验法还是Kendall检验法，这三个变量两两之间的相关系数都比较大，表明两两变量间均具有较强的正相关性，也表明了选取的这三个变量间可通过Copula函数构造联合分布.

选用Gumbel-Hougaard Copula函数、Clayton Copula函数以及Frank Copula函数来构造两变量间的联合分布函数.

对受灾人口(X1)、农作物受灾面积(X2)和直接经济损失(X3)两两变量之间构造Copula联合分布函数，利用RMSE和AIC信息准则检验法，根据其值越小拟合效果越好的检验准则，选出两两变量之间的最优联合分布函数.其中X1-X2、X2-X3和X1-X3的参数拟合优度评价结果见表3.

从表3可知，变量X1-X2、X2-X3和X1-X3均在Clayton Copula函数下的RMSE和AIC值最小，其RMSE最小值分别为0.2893、0.3003和0.2953，AIC最小值分别为0.3307、0.2734和-0.1223.结合RMSE和AIC的判断准则，可得出受灾人口与农作物受灾面积、农作物受灾面积与直接经济损失、受灾人口与直接经济损失变量间都用Clayton Copula函数拟合效果较好.

表3 二维Copula函数的参数及拟合优度

根据X1-X2、X2-X3和X1-X3变量间的最优拟合分布函数，可绘出它们的联合分布函数图，具体见图4-图6.

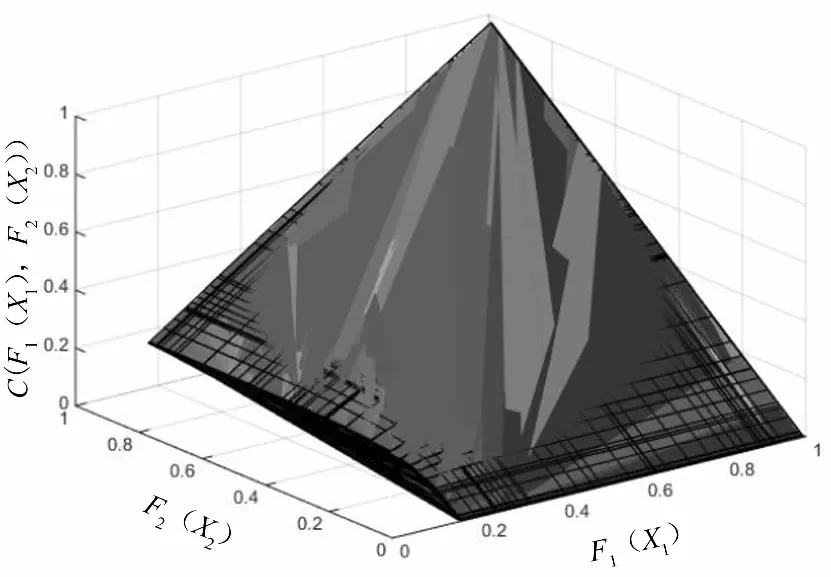
图4 受灾人口与农作物受灾面积的联合分布函数图

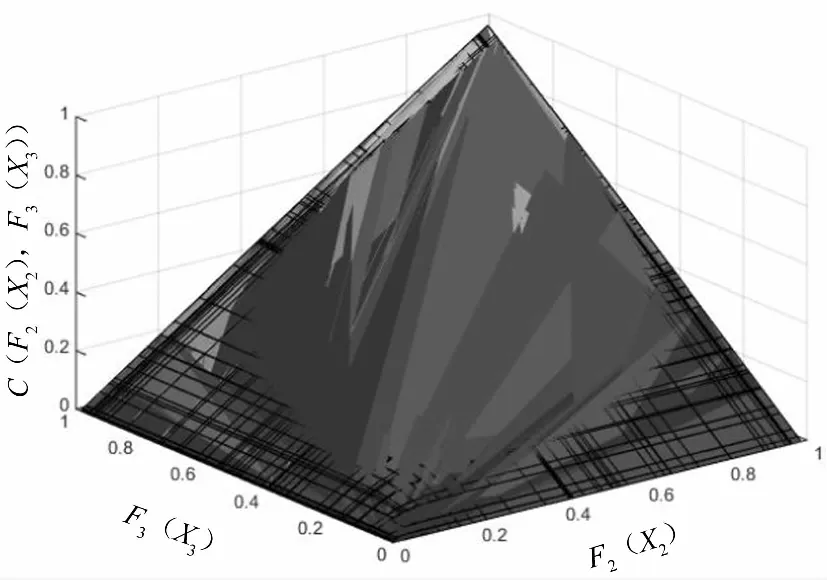
图5 农作物受灾面积与直接经济损失的联合分布函数图

图6 受灾人口与直接经济损失的联合分布函数图

根据图4、图5和图6可分别得出受灾人口和农作物受灾面积、农作物受灾面积和直接经济损失及受灾人口和直接经济损失的联合分布函数图.从图4、图5和图6的图像渐变过程可以看出，颜色越浅，联合分布函数所占的面积越小，联合分布的函数值越接近于1.颜色越深，联合分布函数所占的面积越大，联合分布的函数值越趋于0.如图4所示，随着受灾人口和农作物受灾面积变量的分布函数值增大，其对应的Clayton Copula函数联合分布值就越趋于1.

3.4 三维Copula函数的参数估计及拟合优度检验

采用极大似然法对三维Copula函数的参数进行估计，并利用RMSE和AIC信息准则对所计算的参数进行拟合优度检验.可得三变量Copula函数的参数估计和和拟合优度结果，如表4所示.

表4 三维Copula函数的参数及拟合优度

由以上两种拟合优度检验方法的评价准则和表4可得，三变量用Clayton Copula函数拟合的RMSE值为0.2738、AIC值为-0.0162，这两个评价准则得出的值都是最小的.表明受灾人口、农作物受灾面积和直接经济损失用Clayton Copula函数拟合的效果较好.

3.5 灾情重现期

利用公式(2)-式(4)，结合式(1)，分别求出不同单变量重现期、联合重现期和同现重现期下的受灾人口(X1)、农作物受灾面积(X2)和直接经济损失(X3)的设计值，其计算结果见表5.

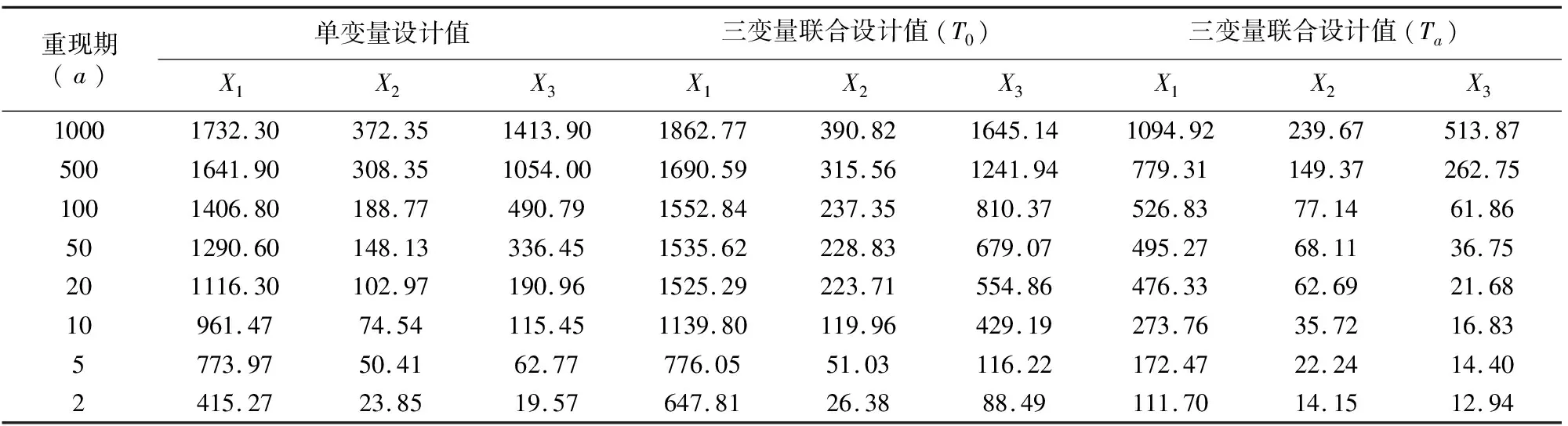
表5 三变量在不同重现期下的设计值

从表5可以发现，在联合重现期下，受灾人口、农作物受灾面积和直接经济损失的设计值都大于单变量重现期和同现重现期下的设计值，表明在预测台风灾害发生的频率时用三变量联合重现期预测台风灾害的发生频率会更加安全，并将其三变量联合重现期记为灾情重现期.

3.6 灾情重现期与台风灾情的比较分析

表6所示的是不同重现期范围内的49个台风个案.因灾情重现期描述的是某类台风灾害发生的频率，通常频率用P表示，以百分比(%)作单位，频率与重现期之间的关系可以表示为P=1/T.对于某种台风灾害来说，其重现期越长意味着这类台风灾害发生的频率越小.

表6 不同重现期范围的台风灾害个例

从表6中可以看到，重现期区间为0～2年时，登陆的台风最多，有35个台风.在重现期区间为2～5年时，有3个台风登陆.在重现期区间为5～10年时，登陆的台风个数为8个.在重现期区间为10～20年时，发生的台风灾害有2个.在重现期区间为20～50年时，发生的台风灾害有1个.

说明重现期越短的台风灾害发生的频率越大，重现期越长的台风灾害发生的频率就越小.

综合单个台风的灾情重现期可以预测台风灾害发生的频率.由表6可知，0518号台风“达维”的灾情因子重现期落在5～10年内，那么可预测在2005年后的5～10年内还会至少出现一次和0518号台风“达维”所造成灾情影响类似的台风灾害.

根据联合重现期的计算公式可得出，0518号台风“达维”的重现期为5.2376年，那么可预测在2011年左右会出现一次与0518号台风“达维”灾情类似的台风灾害.

由表6可知，2011年发生的1117号台风“纳沙”与台风“达维”造成的灾情情况类似.0518号“达维”和1117号“纳沙”台风都为强台风.

以灾情重现期作为判断依据，对2015-2017年华南地区的台风灾情数据进行重现期范围判断，然后再利用公式(3)得出这三年的台风的重现期值，最后台风灾害的重现期区间范围和重现期值进行对比分析，结果见表7.

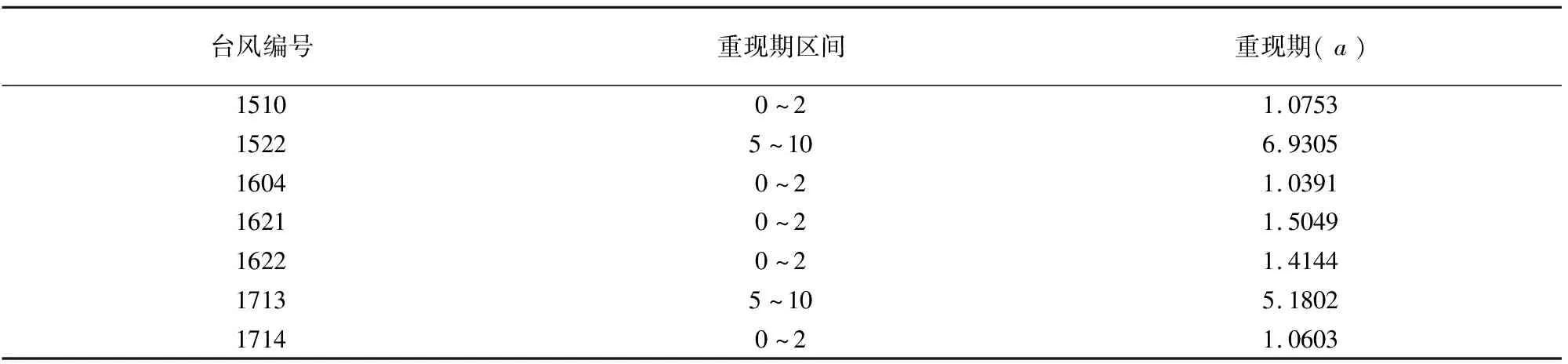
表7 2015-2017年华南地区台风灾害的灾情重现期

根据1117号台风“纳沙”的重现期结果，预测在2017年发生的台风灾害所造成的灾情与其类似.在2017年发生的1713号台风“天鸽”所造成的灾情影响确实如此.

3.7 不同重现期的对比分析

将表6的台风灾情重现期范围下的49个台风与致灾重现期[17]范围下得到的台风进行对比分析.发现有个别的台风灾害的致灾因子重现期和灾情因子重现期落在不同的重现期范围.造成这一现象的主要原因是因为台风灾害造成的灾情不仅受致灾因子的影响，还会受到承灾体因子的影响、当地预报、预防台风的及时性以及灾后救援等客观因素的影响.

对落在致灾重现期的不同重现期范围内的台风数目与落在不同灾情因子重现期范围内的台风数目进行对比分析，具体结果见图7.

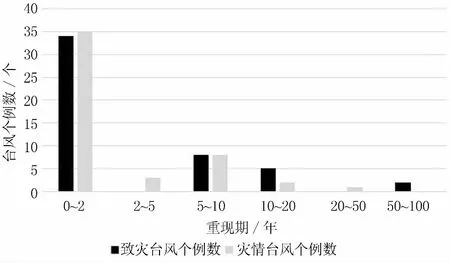
图7 不同重现期范围下的致灾台风与灾情台风

从图7观察到，在致灾重现期与灾情重现期的各阶段重现期范围内，其对应的台风个例总数目相差不大.

综上所述，与之前致灾重现期计算的台风灾害的重现期范围相比，由于其他的致灾因素和客观因素导致存在个别同一编号的台风灾害的重现期范围不一致，但整体上大多数的台风灾害的重现期范围还是一致的.表明利用台风灾情计算的重现期具有一定的可靠性.为了更好地对以后发生的台风灾害进行预测，可结合灾情重现期和致灾重现期进行综合性分析.

4 结 论

选取华南台风灾害的受灾人口、农作物受灾面积和直接经济损失三个灾情影响因子，利用Copula函数的相关理论，构造三维Clayton Copula联合分布函数，计算灾情重现期，分析华南台风灾情，得出以下结论.

对比单变量重现期、联合重现期和同现重现期下的三变量设计值发现，采用三变量联合重现期来分析台风灾情会更加有效.

通过计算华南地区发生的49个台风的灾情重现期，得出台风灾害在重现期0～2年内发生的频率最高，在重现期为20～50年内发生的频率最低.