大额资产清仓的自动化交易策略*
李泽翔,王芷若,舒选林,王颖喆
(北京师范大学 数学科学学院, 北京 100875)
1 引 言
股票市场上的机构投资者出于资产保值增值的目的, 需要在市场上不断地进行资产的买卖交易.如果机构投资者持有的头寸较大, 交易行为本身就会使交易资产供求关系发生变化, 产生价格冲击, 导致交易成本增加.因此, 市场的机构投资者在清仓大额资产时, 需要将交易头寸拆分成批量的订单逐次执行, 而不是采取一次下单交易的方式.同时为了控制资产价值随时间推移产生的波动, 需要在尽可能短的时间内完成清仓.因此需要在价格冲击和时间风险之间进行综合考虑.随着计算机技术的飞速发展, 程序化交易正在以前所未有的速度应用于各国的金融市场中.美国金融市场调查研究显示, 程序化交易已成为美国投资界的主要交易策略.
程序化交易可具体分为确定交易日期和确定日内交易策略两种.艾明芳(2013)[1]详细讨论了如何确定交易持续天数, 但是并没有给出具体的日间交易策略。若计算机在交易当日一次性处理完某类股票, 会导致日内的价格冲击, 造成机构资产不必要的损失.镇磊(2010)[2]虽然具体给出了某支特定股票在交易日内的交易策略, 但是忽略了对于交易持续天数的研究, 这也会一定程度上导致该天的股票交易数量并不是使机构获利最大的交易策略.
随着近几年神经网络不断应用于各个领域, 也有学者将程序化交易与神经网络相结合, Levendovszky 等(2019)[3]利用神经网络预测未来时段的价格分布, 并通过预测结果执行买入与卖出操作, 但只适用于未持有大量某种股票的情况, 对于交易量巨大的情况不能得到全局最优解。Attila(2019)[4]给出了关于减少机器学习股票信息的计算成本的方法, 并提前用ICA对数据进行降噪处理.
在部分借鉴了有关文献对于交易策略制定思路的基础上, 制定出了综合考虑交易持续天数与日内交易时机的交易策略, 并在策略中将神经网络与传统的研究方法相结合.将神经网络用于预测容错率更高的时间风险和交易时刻划分而不是直接预测股票的价值, 不仅一定程度上降低了不准确的学习模型对清仓成本的影响, 还节省了计算机的计算成本.
下面将基于具体实例来建立交易模型。假设在中国A股市场上, 某机构投资者持有工商银行(SH601398)股票10万手, 并且该机构认为目前股票的市价已经处于最高值, 希望在2017年9月26日开始合法清空手中的股票来获得现金收益.以下依据此支股票2017年1月3日至2017年9月25日的分笔交易记录(包括每个交易日各分笔的交易时间、单次交易成交价与交易量、限价订单簿中的第一至第五档买卖方报价及对应的挂单股票数量、以及该分笔交易的触发方), 分析处理交易数据, 给出交易策略.其中对于外部因素(如货币政策等)对股票价格的影响不予考虑, 且假设在清仓过程中不会再购入该股票.
首先确定交易持续的天数, 并据此给出具体的日间交易策略.在确定交易持续天数时, 用神经网络模拟预测清仓时股票价格随时间下降的风险, 用信息流理论模型衡量价格冲击和交易时刻。经综合考虑确定出最终的交易天数以及每个交易日对应的出售股票量.在此基础上, 进行日内交易策略的制定.在此处使用神经网络对交易时刻做出预测, 然后综合考虑VWAP预测出的交易量和Kalman 滤波方法修正过的期权定价公式预测出的各时刻股票的初始价格, 最终给出详细的交易策略及具体的交易成本.
2 交易日内的交易期划分
高频的股票市场数据具有不等时距的特点, 即单笔交易间的时差具有很大的波动性。考虑先将每天内的交易信息按照时间划分成N段, 使得划分出的每一段交易持续期内的成交数量总和大致相等.经过划分的交易期剔除了大量的不可估量的噪声信息。可将每段交易期的长度视作具有一定记忆性的随机变量, 交易越频繁的区域划分出的交易持续期就越短.如果交易期的区间长度过长将会丢失高频的信息, 使模型变得过于粗糙。如果交易期的区间长度太短则会包含过多的噪音, 降低预测结果的可信度.根据经验模型参数的选取[2], 每个交易期的持续长度在5分钟上下浮动, 其总成交数量约占日平均交易量的20倍.因为每个工作日的交易时间为9:30-11:30,13:00-15:00共四个小时, 所以取N=48,即将交易时间划分为48个交易段, 每个交易持续期的长度受当时价格、成交量等市场信息的影响.
3 抛售股票的时机选择
从股票价格随时间下降的风险和价格冲击两方面入手, 分别用神经网络模糊映射方法和多元信息流模型预测两个因素导致的股票价格变动, 从而确定出交易持续天数.根据机构持有的股票数量以及机构为了尽快清理手中股票的目标, 假设清仓时间不超过5天.
3.1 股票价格随时间下降的风险
在预测交易天数时, 只需要考虑日间股票价格下降的风险。先分别对日内各个交易段之间的价格变动做出预测,将此部分数值经适当计算作为每股股票因未售出造成的清仓成本.具体的预测过程如下。
3.1.1 建立模糊映射
股票市场的信息往往带有高度的非线性特征, 使用普通的线性回归的方法并不合理.且金融高频数据内往往存在着明显的日内模式, 即每个交易日的分笔成交时间与数量皆服从一定规律, 相邻交易日的交易区间划分时刻应存在某种映射关系.
这类复杂的模式难以用某个函数显式表达, 而已有理论很好地证明三层的BP(反向传播)神经网络即可高度拟合任意非线性函数.考虑到层数过高会导致计算量过大, 选用三层的BP神经网络, 将交易日内所有交易期的价格向量(ft,1,ft,2,…,ft,47)视作以日为单位的时间序列数据, 并建立相邻交易日间的映射
γ:(ft,1,ft,2,…,ft,47)→(ft+1,1,ft+1,2,…,ft+1,47),
即通过前一天的价格情况预测后一天的价格.
3.1.2 训练BP神经网络
神经网络的训练样本数据集越大, 训练出的模型及预测结果就越精准可靠, 故将167天的所有价格变动数据(ft,1,ft,2,…,ft,47),t=1,2,…,167作为神经网络的训练数据集, 逐天使用输入输出集对(∪k=1,2,…,47mt,k,∪k=1,2,…,47mt+1,k)进行训练.
这里不考虑数据各维度之间的相关性, 即主要对相邻日期内的价格进行研究, 而不考虑同一天内不同交易期间的影响, 突出日间的价格规律的重要性.
第一步 神经网络的激活函数对[0,1]区间内的数值较为灵敏, 为保证模型的精准性, 先将数据归一化,即将每天的价格向量(ft,1,ft,2,…,ft,47)映射到单位球B={x∈:|(xi)|≤1}内, 表示为
用MATLAB工具箱实现上述训练过程后, 得到日间价格关系的模型, 即具有预测未来价格变化功能的BP神经网络.
3.1.3 预测未来的时间风险
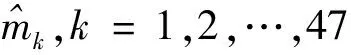
对结果处理后, 得到5天内日间的时间风险, 如表1所示.

表1 未来5天内的时间风险
3.2 价格冲击
投资者在金融市场中迅速大量的买入卖出会影响股票价格, 造成价格冲击现象.为量化交易行为对价格的影响, 参考艾明芳(2013)[1]的信息流理论模型, 使用多元回归分析方法衡量价格的变动.
设t时刻股票价格为pt, 市场中的净指令流为NetVt,Dt=sign(NetVt)表示净指令流的方向, 买入为正, 卖出为负.假设投资者t时刻对净指令流方向的判断仅仅依赖于上一时刻的信息, 有
NetVt=α+βΔpt-1+γNetVt-1+ξt,
其中ξt为t时刻净指令流中投资者依据公开历史信息无法预期的成分,α,β,γ可利用已有数据通过最小二乘法得到.计算结果中的误差项,ξt可以视作交易中根据历史信息无法预期的成分.
借鉴Glosten等(1988)[5]的交易指示模型, 用φ和λ分别表示交易行为造成的永久价格冲击的固定部分系数和可变部分系数, 用θ表示瞬时冲击系数, 即单位股票交易量的变化所引起的瞬间价格下降量, 经艾明芳(2013)[1]推导可得差分方程如式(1)所示.
shock(ΔNetVt)=Δpt=φΔDt+λξt+θΔNetVt+εt.
(1)
其中εt为随机扰动项.使用MATLAB中的最小二乘法拟合回归真实数据得到表2.

表2 价格冲击的参数估计
拟合后得到的回归模型可以较好地表示出股票抛售量与该时刻价格变化的关系.
3.3 确定总交易时长
清仓时间越长, 较小的单次平均抛售量会缓解对市场价格造成的冲击, 但需要承担的时间风险却越大.故需对两个因素进行综合规划, 求得令清仓成本最小的总交易天数.
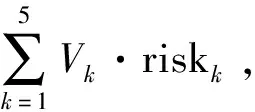
(2)
由式(1)可知shock(ΔNetVk)是关于ΔNetVk的一次函数.这里仅考虑机构抛售股票带来的价格冲击, 因此Dk=-1 , ΔNetVk在此处即为机构每天抛售的股票量Vk.利用Mathematica中的Minimize函数, 可求得最优解V1,…,V5,具体结果如表3所示, 其中V3=V4=V5=0, 也就是说该股票的最优交易天数为2天.

表3 交易时长与交易量分配
4 出售资产的自动化交易策略
4.1 模拟自动交易时间
为捕捉交易期长度的日间自相关现象, 考虑相邻交易日交易时刻向量间的映射关系, 利用神经网络模型建立式(3)所示的一元映射.
Q:xt,k→xt+1,k,t=1,2,…,167,k=1,2,…,48,
(3)
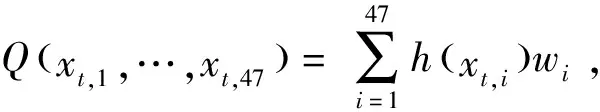

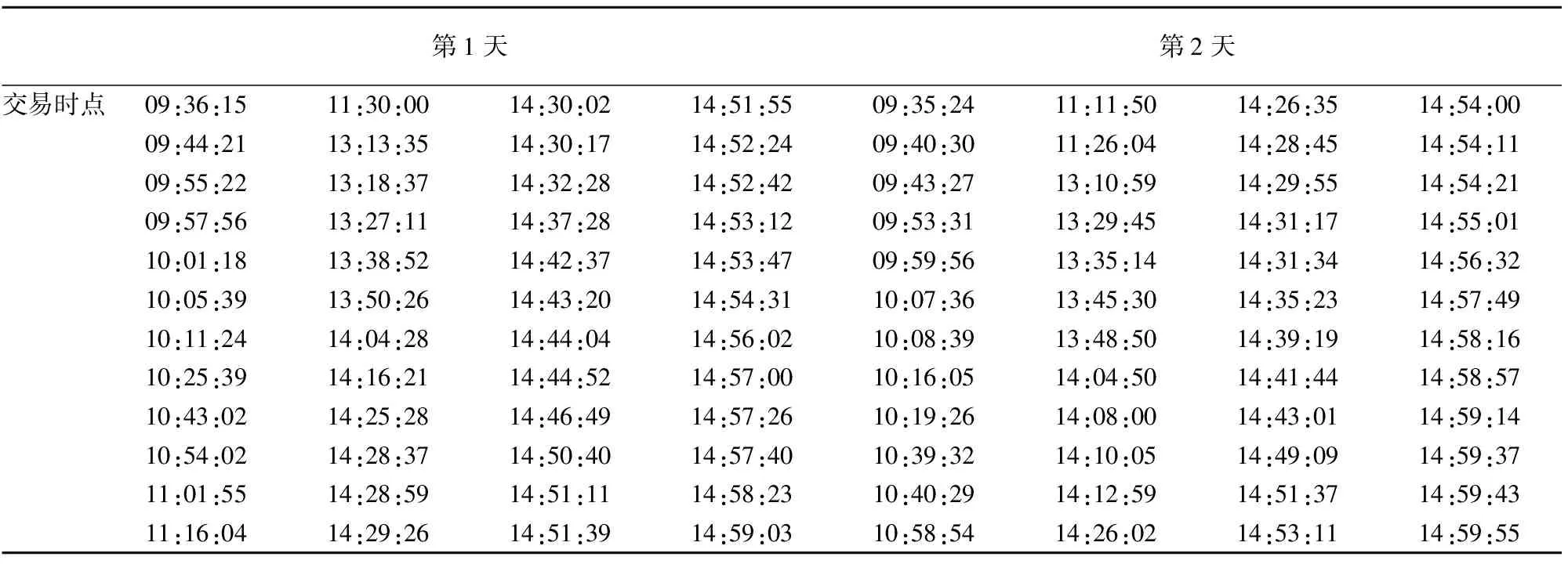
表4 预测的交易时间点
表中的“09:36:15” 表示当天第一个交易期的截止时间点, 即9点30分到9点36分15秒为该交易日的第一个交易期.
4.2 预测交易量
4.2.1 VWAP算法预测市场交易量
考虑到不同交易区间的记忆周期存在明显的区别, 若用常规的交易量加权平均价格算法来预测日内交易量, 可能会产生较大的偏差, 故采用基于自回归的分时VWAP算法, 分别对每个交易期内的总成交量Vt,k进行时间上的自回归分析.
首先利用Mathematica中的UnitRootTest检验时间序列的平稳性, 确认历史数据适用于自回归模型.利用STATA中的ac图像与pac图像, 结合Mathematica中TimeSeriesModelFit函数给出的模型结果, 判断出股票可以使用具有3阶时滞的AR模型Vt,k=a0+a1Vt-1,k+a2Vt-2,k+a3Vt-3,k进行拟合.利用STATA回归拟合并检验, 保留影响显著的参数后得到股票交易量的自影响机制,见式(4).
Vt,k=10342.8+0.241Vt-1,k+0.296Vt-2,k+0.0762Vt-3,k.
(4)
利用历史数据, 对9月25日后两个交易日的每个交易期的交易量进行初步预测, 得到的交易量分布如表5所示.
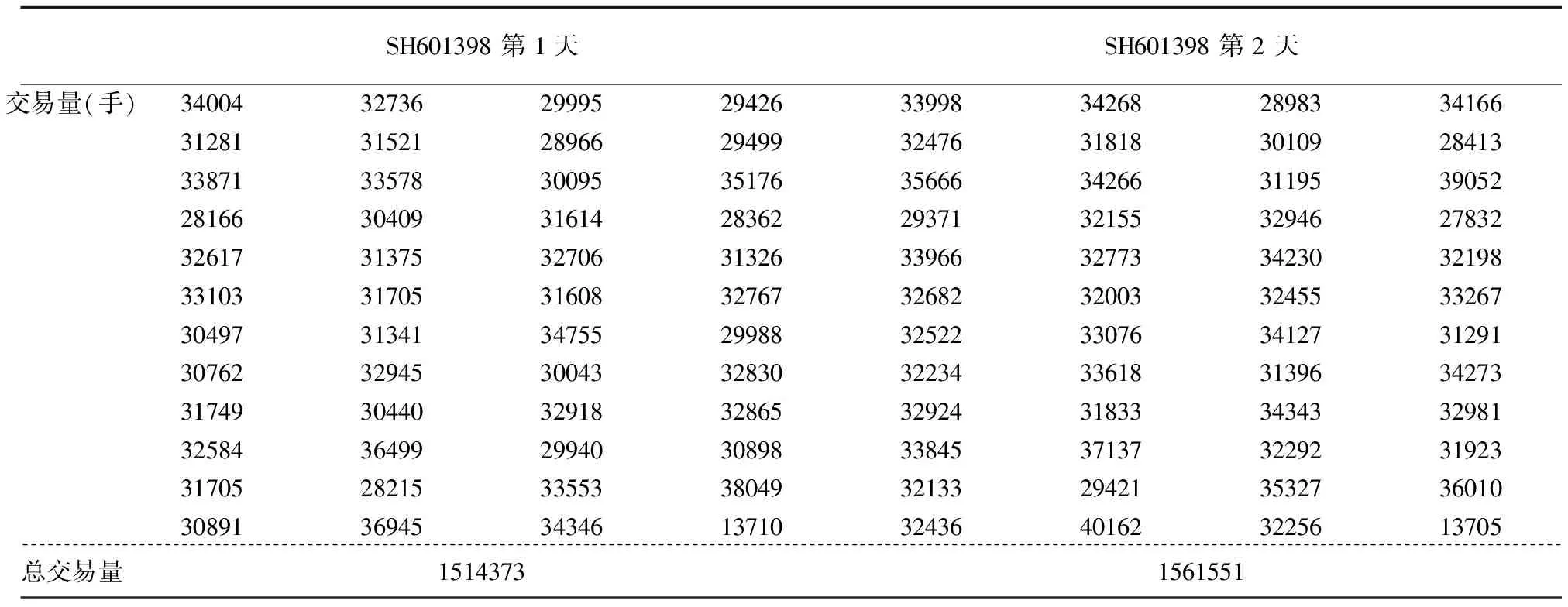
表5 预测的总交易量
表中的 “34004” 表示在表4所示的第一个交易期中市场上关于”SH601398” 的交易量为34004手.
4.2.2 确定机构投资者预期出售量
基于投资者的出售行为总是理性的假设, 当市场交易量大时抛售更多的股票、市场交易量小时出售较少的股票, 可以遵循市场的波动规律, 减少自身行为造成的价格下降.可以考虑在每个交易期内的抛出量占所有股数的比例与该交易期内该股的成交量占该股全天总成交量的比例相同.
4.3 股票初始价格预测
股票的短期价格往往会围绕其当期总体平均水平上下浮动, 而长期的价格走势很大程度上会受到市场交易情况的影响.9月25日之前股票价格的持续走高, 很可能是市场中热度不断提高的股票买卖交易造成的.若不考虑其他外部因素的影响, 从9月26日开始的价格水平下跌, 则是因为该公司股票抛售行为导致的瞬时和永久性价格冲击.所以资产清仓开始时的股票价格应为短期内的上限, 并在后续几日内呈整体下降的走势.若要确定不受市场交易情况影响时的股票成交价格, 只需分析一定时期内股票价格情况的变化规律, 即从真实的成交价格中刨除由于公司抛售股票(并可能引发更多投资者跟风抛售)造成的价格变动部分.
使用期权定价公式, 即带有漂移项的布朗运动模型dP(t)=at+dB(t)对9月25日之前的股票价格数据进行拟合.去除因为若干外部不可测因素带来的价格走势升高(即正向漂移项部分), 剩下的随机运动部分表示价格的波动状况.分别选用不同的布朗运动方程分别对48个交易期的日间规律进行刻画, 即Pk(t+1)=Pk(t)+akt+dBk(t).
考虑到预测模型本身也带有不确定性, 参考Kalman滤波, 对于选定的第k=k0交易期, 首先使用期权定价公式与第t天的信息, 计算第t+1天第k0交易期的初始成交价格预测值, 再用第t+1天市场成交真实价格对该模型进行修正.
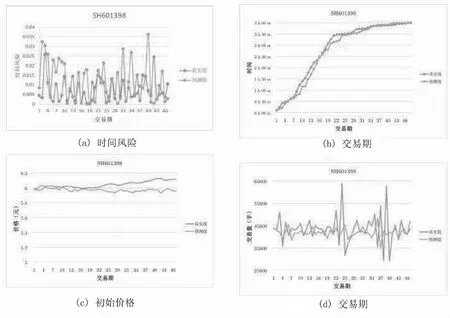
某交易期的成交均价实际为一个随机变量, 假设其皆服从均值为μt、方差为σt的正态分布。股票价格的历史数据实际上是真实水平与随机因素叠加后的结果,可将已知数据视作服从正态分布的随机变量q(t)=xt+e,e~N(0,r)的抽样,其均值xt为真实的价格水平, 方差r的大小则代表数据的准确程度.但不论如何, 历史数据的可信程度应当高于由预测模型推导得到的结果, 即满足σt 确定价格预测模型dP(t)=at+dB(t), dP(t)=P(t-1)+a(t-1)+dB(t),dB(t)~N(0,q),P(t-1)~N(μt-1,σt-1). 通过公式可得第t天的价格分布的期望μt=μt-1+a(t-1)和方差σt=σt-1+q. 过去的成交价格q(t)=cyt+e,c=1, 是价格真实水平yt和随机因素e,e~N(0,r)的叠加, 故q(t)~N(yt,r). 在原始的预测模型中纳入了精度更高的历史交易数据, 通过原模型得到的价格的期望要根据历史数据进行相应调整.因为已知信息更多, 故可相应提高预测结果的精度, 即最终得到的价格分布的方差相应减小.价格分布的期望调整为 其方差相应地调整为 故在对全部历史数据进行上述操作后, 即可得到较为精准的价格预测模型 P(t)=P(t-1)+a(t-1)+dB(t),dB(t)~N(0,q),P(t-1)~N(μ,σ). 再通过之前的交易数据, 对9月25日后两个交易日中48个交易期内的初始的成交价格进行预测, 结果如表6所示. 表6 初始价格预测 表中 ”5.97” 表示在表4所示的第一个交易期中市场上关于”SH601398” 的交易价格为5.97元. 仿照以上步骤, 依次修正后续k-2个交易期的成交价与成交量, 得到最终的价格和交易量分布. 利用MATLAB编写程序, 实现上述价格、市场成交量与投资者抛售量的调整过程.选取中等程度的风险容忍程度系数a=0.5.计算得到最终的价格和交易量分布, 并给出表7所示的程序化交易策略. 表7 程序化交易策略 表7的交易时间和价格和前面表中的含义一致, 交易量为该机构在每个交易期抛售的股票数量.例如在第一个交易日的第一个交易期该机构抛售的股票数量为1105手. 最终计算得到股票的交易成本为1173500元. 为了验证建模方法的合理性, 基于前166天(1月3日至9月24日)的数据给出第167天(9月25日)的预测, 并用预测结果与真实数据进行比对.各部分的比对情况见图1. 图1 自动化交易策略的有效性检验 对比分析发现, 历史真实数据与制定策略下的交易时刻与价格情况大致吻合, 说明此策略具有一定的合理性, 即依此策略售股的投资者可期望得到最大的现金收益. 此处的自动化交易策略虽然是在一定的假设条件下给出的, 并且离应用在股票市场上还有一段不小的距离, 但是为资产清仓算法提供了一种新思路.将神经网络和传统方法相结合, 操作简便, 计算机易于执行的神经网络替换掉了传统方法中一部分复杂的计算, 使得算法的自动化程度更高.此外, 还综合考虑了总清仓时间以及日内清仓的具体交易策略, 更加贴近机构清仓大额资产时的实际情况.今后的研究目标是在现有基础上逐步放宽模型的假设条件, 使其更加贴近或几乎近似股票交易市场的实际情况.
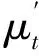
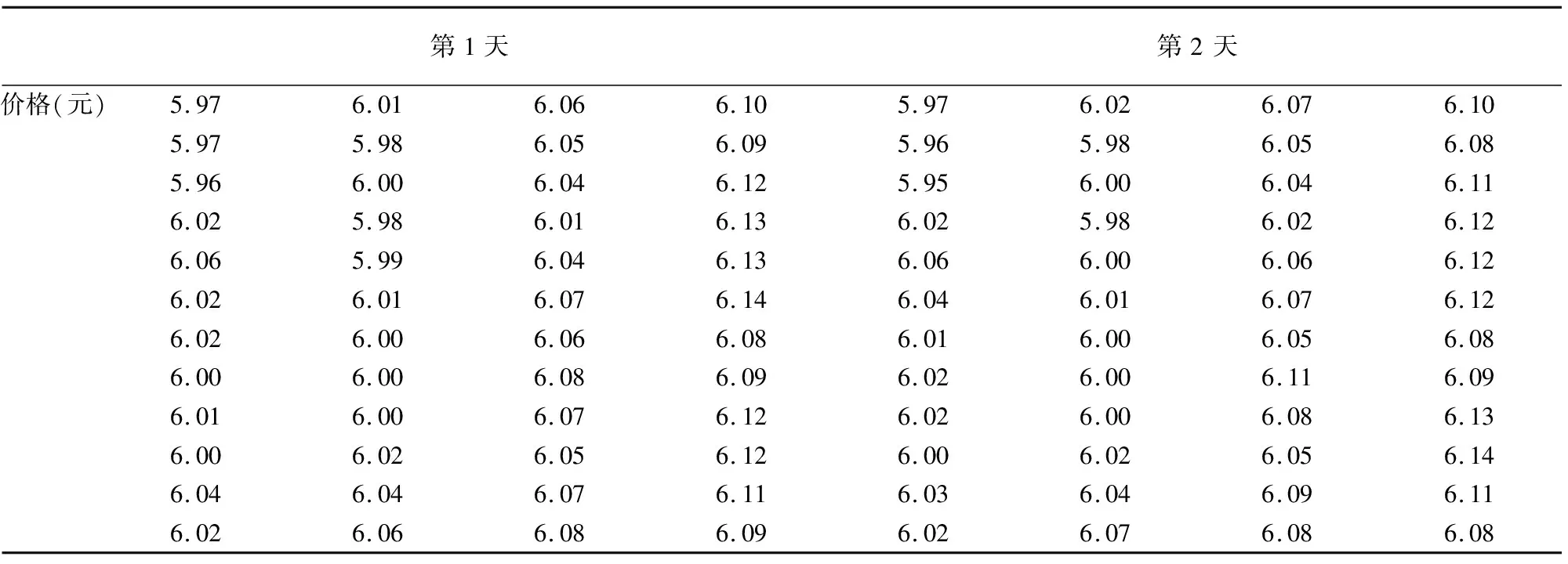
4. 4 调整成交价格与数量

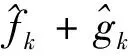
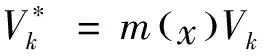
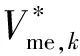
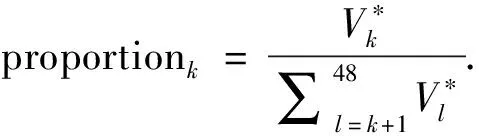
4.5 自动化交易策略
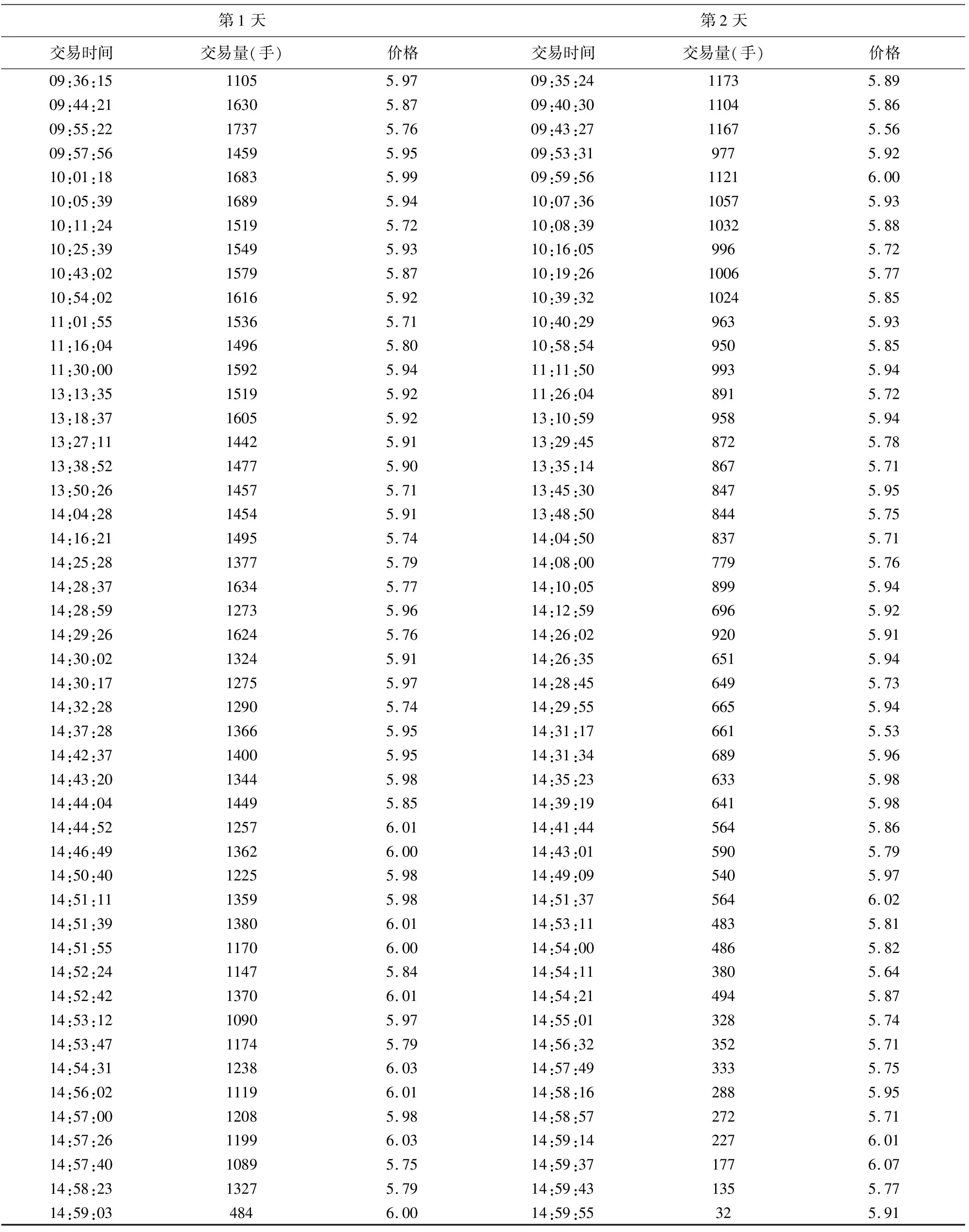
5 自动化交易策略的有效性检验
5 结 论

