一种新的死亡率模型及基于中国人口数据的比较分析*

马海飞，肖鸿民,赵弘宇

(西北师范大学 数学与统计学院,甘肃 兰州 730070)

1 引 言

死亡率、出生率和移民是决定人口规模、结构和分布变化的主要因素.近几十年来, 随着社会经济的不断发展和医疗水平的进一步提升, 人口死亡率逐渐降低, 致使老龄化问题越来越严重.人均寿命的不断提高, 可能会使寿险公司和养老金机构在终身年金业务上面临巨大的损失, 进而影响整个社会经济的发展.因此, 在未来长期以及中短期规划中, 人口预测是至关重要的.

死亡率预测作为一个重要的人口因素, 被广泛应用于各个领域.尤其是对于寿险企业而言, 为了最大化利润, 同时成功避免可能的风险, 养老金计划和人寿保险产品的定价需要准确预测未来死亡率，这促使研究人员不断地调查人口数据、建立预测模型、拟合模型和预测未来死亡率.近几十年来, 死亡率预测技术有了很大的发展和提高.在国外, Lee等(1992)[1]提出的Lee-Carter模型, 是一种将人口统计模型和时间序列联系起来的对数双线性模型.Renshaw等(2006)[2]在Lee-Carter模型的基础上加入了出生年效应, 首次提出了RH模型并将其应用到英格兰和威尔士男性死亡率预测中.Cairns等(2011)[3]通过对6个随机死亡率模型的分析, 发现要从拟合和预测两个方面来判定一个模型的合理性.Li等(2013)[4]运用扩展的Lee-Carter方法对美国和日本死亡率数据进行拟合与预测.Enchev等(2017)[5]利用6个国家的死亡率数据对共同年龄效应(CAE)等随机死亡率模型的拟合效果进行比较, 通过模型预测发现CAE模型最优.Li等(2019)[6]运用一个新的双人口死亡率预测模型对比利时、瑞典、瑞士和英国4个国家的高龄死亡率数据进行了拟合与预测.在国内研究中, 李志生等(2010)[7]运用Lee-Carter模型对中国人口死亡率数据进行拟合和预测, 之后黄顺林等(2010)[8]运用RH模型对中国男性人口死亡率进行了预测,并将其应用到预期寿命和年金系数的估计中.韩猛等(2010)[9]对Lee-Carter模型进行了改进,通过一个双随机过程对Lee-Carter模型中的时间项进行建模.曾燕等(2016)[10]采用Bootstrap方法与Lee-Carter模型拟合死亡率数据,运用带漂移项的随机游走模型进行预测.曹园(2018)[11]用Lee-Carter模型对中国人口死亡率进行预测后,根据预测的死亡率数据对中国人口平均预期寿命进行计算.樊毅和张宁等(2018)[12]基于中国人口死亡率数据, 对8个死亡率经典模型进行了比较分析, 发现APC模型对中国人口死亡率的拟合效果最优.王晓军等(2019)[13]运用台湾高龄人口死亡率数据对贝叶斯分层模型等8种死亡率模型进行了比较分析, 最后通过拟合中国大陆人口数据, 发现CBD模型对我国大陆地区高龄死亡率的拟合和预测较好.

到目前为止, 关于中国人口数据的死亡率模型研究, 都依赖于LC和APC等几个常见的随机死亡率模型, 模型可选择性受到约束.本文的主要工作是对APC模型进行扩展, 提出一个新的死亡率模型——EPAC(Extended Age-Period-Cohort), 通过比较模型的拟合效果和预测效果, 并对其稳定性进行检验, 发现EAPC模型更适合于拟合和预测中国的人口死亡率.在论文第二部分将介绍EPAC模型, 第三部分对新模型的拟合效果的与LC和APC进行比较分析, 第四部分是预测效果的比较分析.

2 随机死亡率模型

2.1 模型简介

在理论研究上比较成熟且出现最早的随机死亡率模型是Lee and Carter(1992)提出的Lee-Carter模型, 将死亡率的变动跟年龄因子和年份因子结合在一起, 简记为LC模型.具体形式如下:

lnmx,t=αx+βxkt+εx,t.

(1)

其中,mx,t表示时间为t年龄为x岁人群的中心死亡率;αx为依赖年龄因子的参数,表示x岁人口对数死亡率的平均数;βx表示年龄因子对时间的敏感度;kt反映死亡率随时间t的变化程度,通常称为死亡指数,可以看成一个ARIMA过程或随机游走过程;εx,t为随机误差项.

Currie(2006)提出了一个带出生年效应的死亡率模型,即Age-Period-Cohort模型(APC模型),其具体形式如下：

lnmx,t=αx+kt+γt-x.

(2)

其中,γt-x是一个出生年效应, 表示出生年(t-x)对死亡率的影响, 其他符号与参数意义同前文相同.

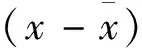
(3)

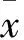
2.2 参数估计

对上述随机死亡率模型进行参数估计时, 都假定死亡人数Dx,t服从参数为λx,t的泊松分布,λx,t=mx,tEx,t,即

Dx,t～Possion(mx,tEx,t).

(4)

其中,Dx,t表示年龄为x时间为t的死亡人数,Ex,t表示年龄为x时间为t的平均暴露人数.对于一个给定的模型, 用θ来代表待估计的参数向量, 符号mx,t扩展成mx,t,θ来代表参数之间的依赖性.对于所有的模型都可以通过极大似然估计方法进行参数估计,其对数似然函数形式如下：

L(θ,D,E)=∑x,t[Dx,tln(Ex,tmx,t,θ)-Ex,tmx,t,θ]+constant.

(5)

最后运用牛顿迭代法得到各参数的估计值, 牛顿迭代公式如下：

(6)

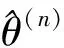
(7)

(8)

(9)

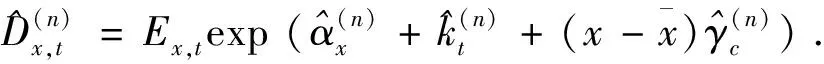
3 死亡率模型拟合效果的比较分析

3.1 经验死亡率数据

本文采用的原始数据来源于1996-2018年的《中国人口统计年鉴》.对于选取的连续23年的中国人口0～90岁死亡率数据, 由于大部分日历年数据的末组都为90+(90岁及以上用90+表示),所以本文的年龄上限设为90,其中1996年数据的最高年龄是85岁以上,对于数据不足90+的部分,用均值插值法进行补充处理,对1995，2000，2005和2010年数据中100岁以上(包括100岁)的部分进行合并处理.根据这些数据绘制了分年龄死亡率图, 见图1.

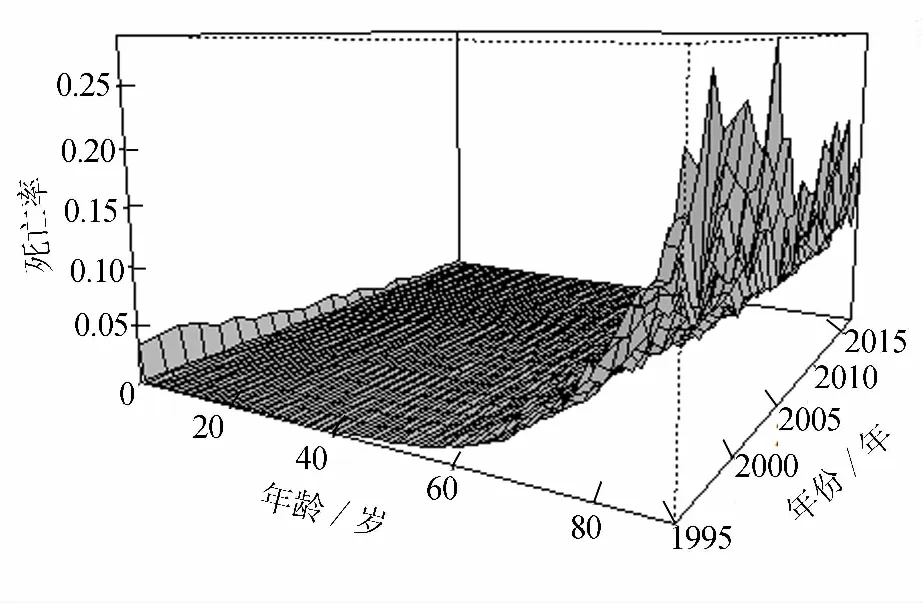
图1 1995-2017年中国人口死亡率图

从图1可以看出, 死亡率随着年龄的增长呈现出先降低再逐渐上升的趋势.同时, 随着时间的推移, 每个年龄的死亡率表现出降低的趋势, 这说明死亡率在逐渐改善, 不过改善程度在不同年龄存在较大的差异, 接下来将利用随机死亡率模型对上述死亡率数据进行拟合与预测.

3.2 参数估计

在上述数据中选取1995-2014年的死亡率数据, 结合式(6)分别对LC模型、APC模型和EAPC模型的参数进行估计, 结果如图2所示.

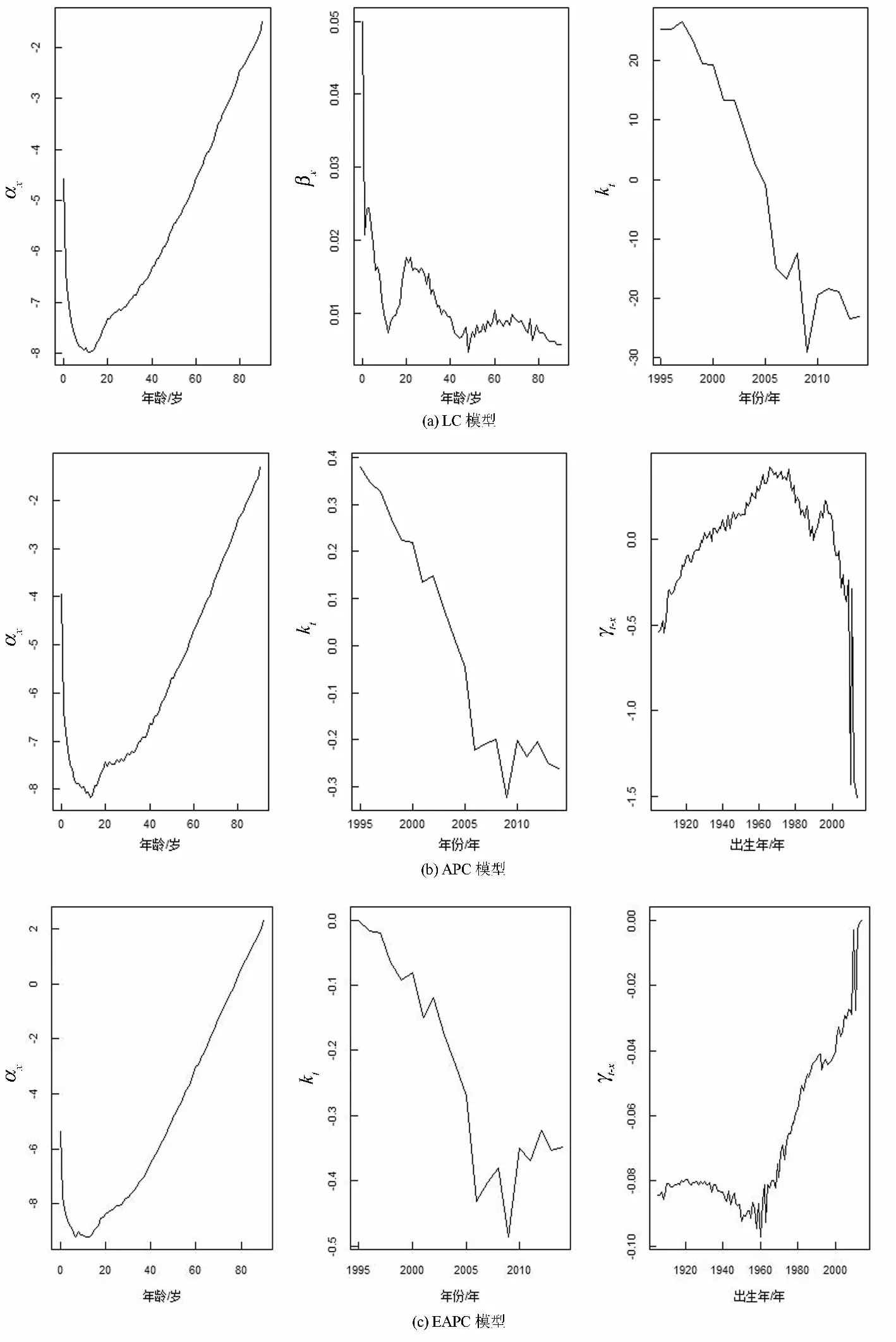
图2 LC模型、APC模型和EAPC模型参数估计图

3.3 死亡率模型拟合效果的比较

图3是LC模型、APC模型和EAPC模型拟合的残差图.总的来看, 3个模型都较好地捕捉到了年龄效应和时间效应, APC模型和EAPC模型捕捉到了出生年效应, LC模型中出生年效应的残差有轻微的波动, 说明该模型未能较好地捕捉出生年效应.所以从模型拟合的残差图可以看出, APC模型和EAPC模型的拟合效果相对较好.

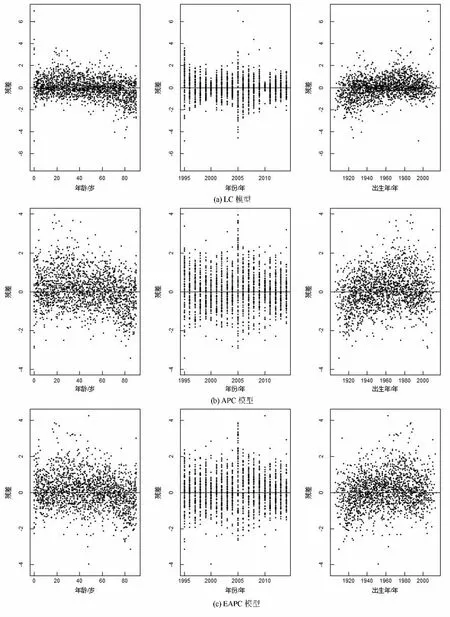
图3 LC模型、APC模型和EAPC模型的残差图

为了更直观地比较模型拟合的效果, 定义绝对拟合误差(Absolute Fitting Error, AFE)为死亡率拟合值与实际死亡率差的绝对值之和, AFE的定义式如下:

(10)

表1给出了3个死亡率模型的绝对拟合误差及其AIC和BIC值, 其中APC模型的绝对拟合误差为3.7863, LC模型的拟合误差比APC模型的绝对拟合误差大, EAPC模型的绝对拟合误差为3.7817, 略低于APC模型的拟合误差值.从另一方面来看, LC模型的AIC和BIC信息值分别为17469.39和18570.71, 而APC模型和EAPC模型的信息值均低于LC模型的信息值.由此可见, APC模型和EAPC模型的拟合效果较好.

表1 死亡率模型的AFE、AIC和BIC值

4 死亡率模型预测效果的比较分析

4.1 死亡率预测

APC模型和EAPC模型中死亡率的动态变化受时间指数和出生年指数的影响, 因此预测未来死亡率需要使用时间序列的处理方法进行建模.对于上述两种模型的时间因素kt, 使用带漂移项的随机游走过程进行拟合, 而对于出生年效应γt-x, 假设它独立于kt，服从一个ARIMA过程.图4是APC模型和EAPC模型参数kt和γt-x未来3年的预测值.

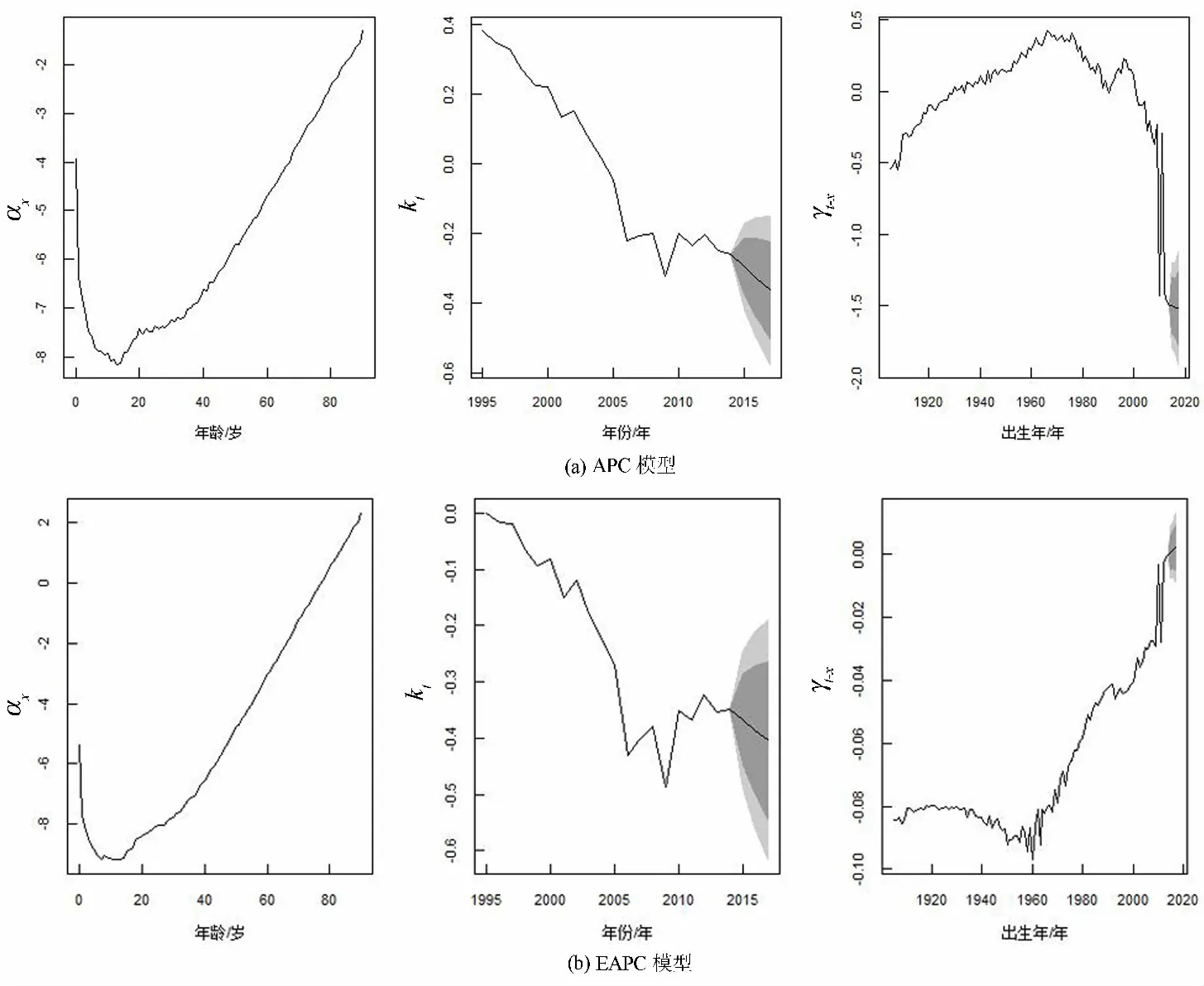
图4 APC模型和EAPC模型参数kt和γt-x的预测值

将上述序列kt和γt-x的预测值分别代入式(2)和(3)中, 可以得到2015-2024年中国人口死亡率预测值.选取2016年和2017年的死亡率预测值与真实值做对比, 结果如图5所示.从图中可以看出, APC模型与EAPC模型在65岁以下的死亡率预测值与真实值非常接近, 预测效果较好.但在65岁以上的高年龄组中, 两个模型的死亡率预测值均略高于真实值, 这是由于本文所用数据截至90+,对原始数据中更高年龄组,用合并的方式重新计算了死亡率数据,故存在少量偏差.

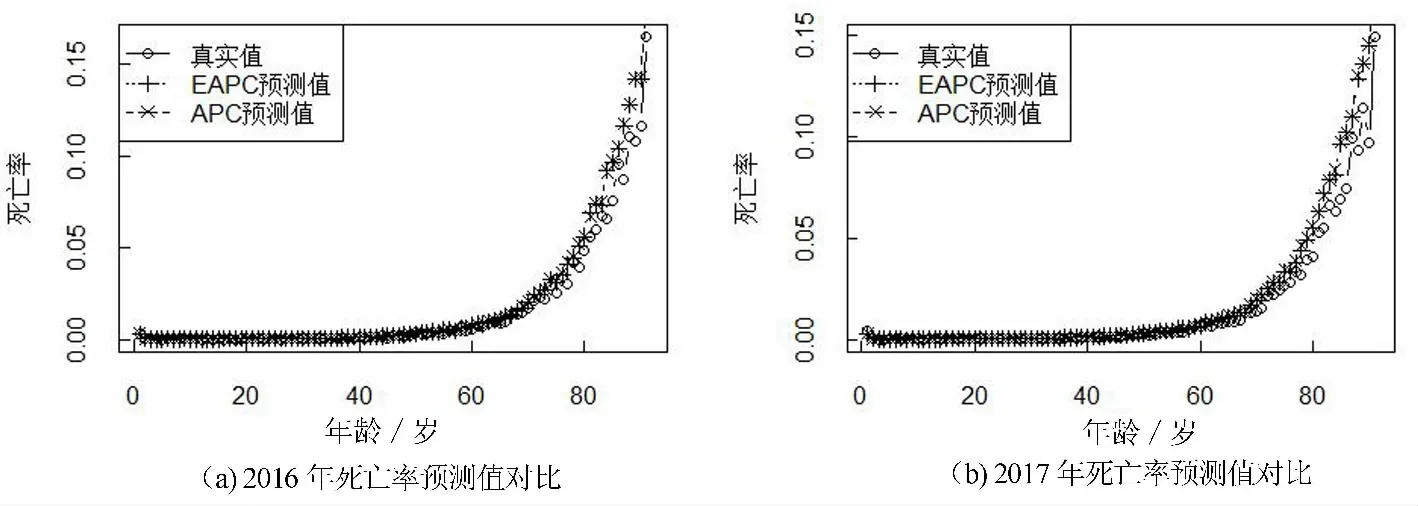
图5 2016和2017年死亡率预测值与真实值对比

4.2 死亡率模型预测效果的比较

为了更直观地比较上述两种死亡率模型在高年龄组的预测效果, 根据2015-2017年APC模型和EAPC模型的死亡率预测值, 作出年龄分别为65岁、75岁和85岁时, 死亡率预测值与真实值的对比图, 如图6所示.从图中可以看出, 在高年龄组中, EAPC模型的曲线介于真实值与APC模型的曲线之间, 也就是说EAPC模型的预测值更接近真实值, 所以 EAPC模型的预测效果较好.

图6 65，75和85岁死亡率预测值与真实值对比

4.3 预测结果的稳定性检验

从上述各方面来看, EAPC模型表现较好, 不过还需对其进行稳定性检验, 需要比较用1995-2014年的数据拟合得到的预测结果和用1999-2014年的数据拟合得到的预测结果.如果模型是稳定的, 那么减少4年的数据不会对预测结果产生太多影响.本文用这两组数据估计了EAPC模型在x=0, 15, 65, 90岁情况下的死亡率预测值(见图7).根据1995-2014年数据估计出来的预测值记为EAPC, 根据1999-2014年数据估计出来的预测值记为EAPC*.

从图7可以看出, 死亡率预测值随着时间的推移而逐渐下降, 说明死亡率随着年份的变化逐渐改善, 符合人口死亡率数据变化的趋势.而且，EAPC模型使用两组不同的数据在4个年龄上得到的预测值非常相似, 没有明显变化, 这说明这个模型在预测上是稳定的.

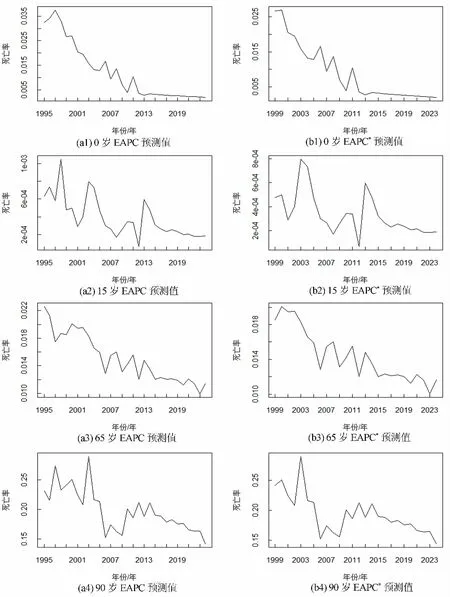
图7 EAPC模型预测的稳定性比较图

5 结 论

本文在APC模型的基础上进行优化得到EAPC模型, 并结合中国人口死亡率数据, 比较该新模型与LC模型和APC模型的拟合与预测效果.

从拟合方面来看, APC模型和EAPC模型较好地捕捉到了出生年效应, 其残差图更稳定.通过进一步计算模型的AIC和BIC值, 发现APC模型和EAPC模型优于LC模型, 所以用EAPC模型来拟合中国人口死亡率是比较可靠的.

从预测方面来看, APC模型和EAPC模型的预测值与真实值均非常接近, 而且在高年龄组中, EAPC的预测效果优于APC模型.通过进一步对EAPC模型的预测结果进行稳定性检验, 发现EAPC模型在减少4年数据的情况下, 预测结果没有太大变化, 说明EAPC模型在一定程度上是稳定的.

所以, 从EAPC模型的拟合效果和预测效果可以看出, EAPC模型更适合于中国人口死亡率的拟合与预测, 也就是说作为由APC模型扩展而来的一种新模型, EAPC模型可以广泛应用于中国人口死亡率的预测之中.