高频数据连续部分杠杆效应的估计*

肖鸿民，康宏亮

(西北师范大学 数学与统计学院，甘肃 兰州 730070)

1 引 言

Bollersler等(2006)[1]利用5分钟股票样本找到了波动率与股票对数价格的负相关关系.Jacod和Tadoror(2010)[2]在有限的增量前提下,利用瞬时波动率估计作为中间变量,对杠杆效应进行了研究.Wang和Mykland(2014)[3]在连续时间条件下定义了杠杆效应并对之进行了非参数估计,然而只是在连续时间下进行讨论,并未对非连续时间情况进行说明.Vetter(2015)[4]基于瞬时波动率估计量的增量,对积分波动率的波动进行了非参数估计.Xiu和 Kalnina(2015)[5]采用相似的方法,用自己定义的函数来代替波动率过程,然而,这种方法的最大问题在于所选函数不能有效模拟波动过程,尤其是在市场微观结构噪声的影响下.Eraker(2003)[6]对非连续时间下的杠杆效应进行了讨论.但这种方法对于跳跃过程的假设有时并不恰当。Bandi 与 Reno′(2012)[7]在文中提及了“co-jump leverage”,但并未对“co-jump leverage”的估计进行证明.

目前对杠杆效应的检测性研究相对成熟,对杠杆效应的度量方面的研究正处于探索阶段,如何估计杠杆效应已成为很有意义的研究课题.运用估计方法来量化一般连续时间情况下的杠杆效应(CLE),结合概率极限、随机过程理论、临近窗口和向下截断思想构造了连续部分杠杆效应(CLE)估计量,说明了该估计量的相合性和渐近正态性,并给出了证明.

2 跳-扩散模型的建立和杠杆效应的定义

2.1 跳-扩散模型的建立

定义在概率空间(Ω,F,(Ft)t≥0,P)上的对数资产价格过程(Xt)t≥0和波动率过程(σt)t≥0满足如下的It半鞅过程

(1)

(2)

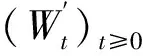
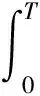
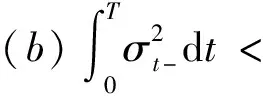
(c)所有的样本路径

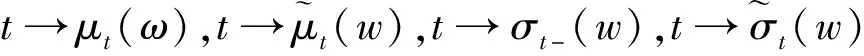
2.2 杠杆效应的定义

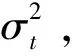
(3)

(4)

(5)

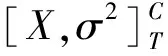
3 CLE估计量的构造

假定数据是等间隔Δn=T/n观测的,且没有测量误差的存在,包含所有观测时间点的所有分割如下

(6)

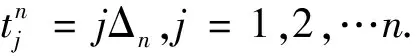
寻找一列窗口kn,kn为整数.对正常数K,满足

(7)

令

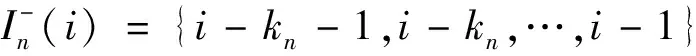
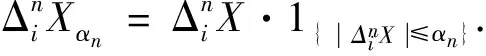
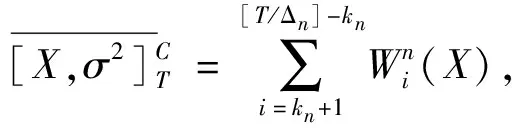
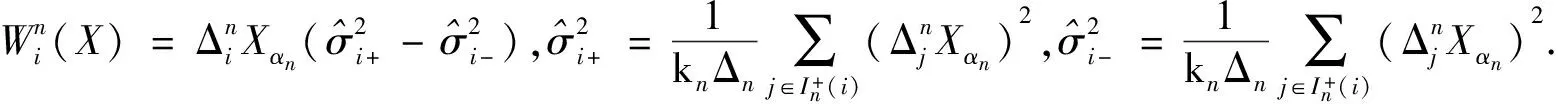
4 CLE估计量的相合性

定理1假定

(a)X是连续的并且σ2的跳跃部分有有限的总变差，

(b)式(1)、式(2)和式(7)的假设成立.

当(a)，(b)成立时,则有

5 CLE估计量的渐近正态性

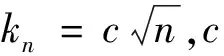
(a)X是连续的并且σ2的跳跃部分有有限的总变差,

(b)式(1)和式(2)的假设成立.

当(a),(b)成立时,有

其中B是标准wiener过程且与F独立,且

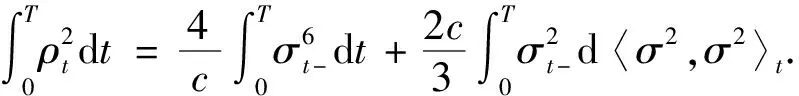
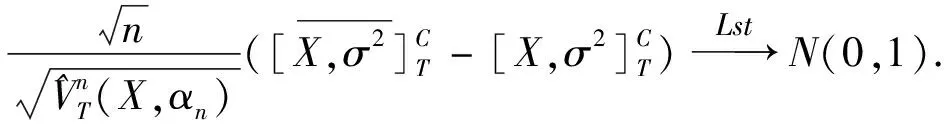
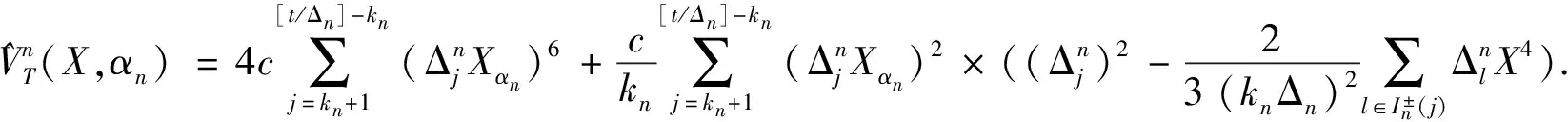
6 定理的证明

将波动率过程表述为

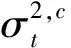
(9)

定理2的证明如下.

首先,证明截断误差和离散误差依概率收敛到零, 而波动率误差依概率收敛到极限过程.

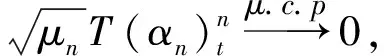
因为

不难证明

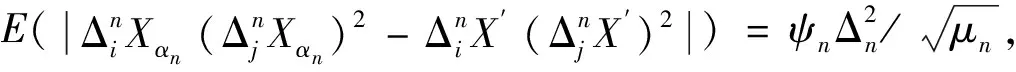
考虑函数F(xi,xj)=xi(xj)2和如下的向量：

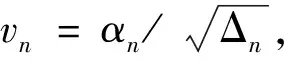
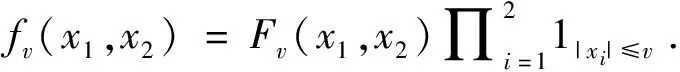
当r<1,m=s=1,s′=p′=2,对l=1,2,

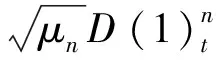
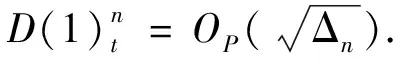
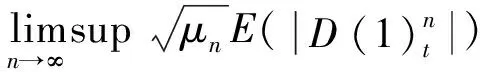
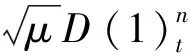
第三步证明

由Cauchy-Schwardz 不等式

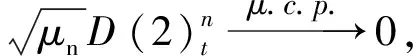
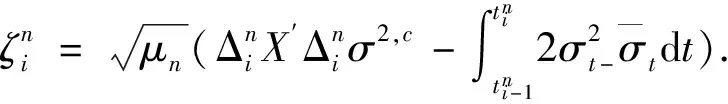
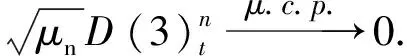
第四步定义

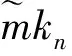
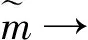
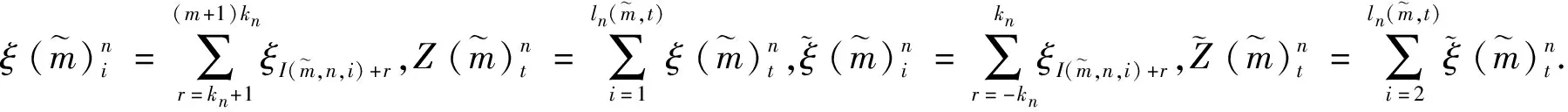
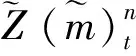
根据连续性条件, 得

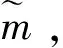
并且

上式右边第一项为Op(knΔn).对于第二项, 当j>r时, 根据连续性条件, 可得

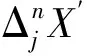
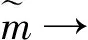
接下来证明

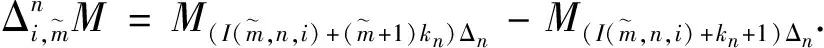
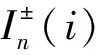
进一步, 令

易证得

因此, 根据连续性条件得

四阶矩的计算比较繁琐, 只给出部分结果，并省略这些结果的计算过程.

=KtΔn→0,

当M=W或M=B时, 根据连续性条件, 可得

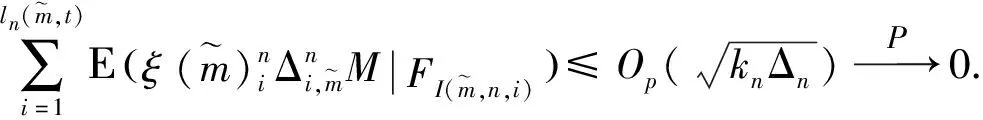
因此, 结论已成立.

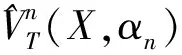
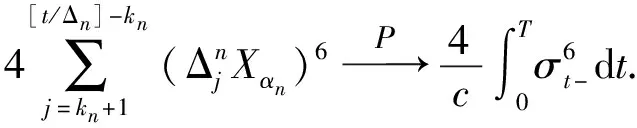
基于这些结果,可得

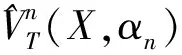
定理 1 的证明

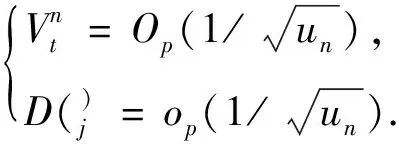
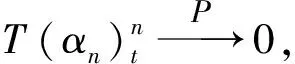
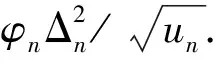
7 结 论