例析数学思想方法在AMC概率题中的应用*

韦娟娟

(江苏省扬州大学数学科学学院,225002)

数学思想方法是更高层次的数学知识,是解决数学问题的隐性的、抽象的观念,是数学的灵魂、本质所在,对学生数学认知的完善,思维、能力的发展具有积极的意义[1]．教学中重视将其渗透,能帮助学生把握问题本质,融汇贯通,提升分析和解决问题的能力．

每年一度的美国中学数学竞赛(简称AMC)分别针对八年级、十年级和十二年级的学生开展,每个年级的竞赛试题均为25题,其中对概率问题是必考题,通常为2-3题．研究历届AMC试题中的概率题，发现这些概率问题解答体现了丰富的数学思想方法．本文以AMC中的概率问题为例,解析转化与化归思想、对称思想、方程思想、递归思想在概率问题中的渗透与应用,以期帮助读者增强应用数学思想方法的意识和能力．

一、转化与化归思想

转化与化归是一种基本的数学思想方法,其实质是实现数学中矛盾的转化,化繁为简、化难为易，将复杂陌生的问题情境转化为自己熟悉的、易解决的问题[2]．概率中常见的转化有事件的转化、模型的转化,例如考虑对立事件,联想概率中的常见模型:掷骰子、摸球模型等,回忆已解决的概率问题等．

例1七个标准的6面骰子被抛掷,求正面朝上的点数之和为10的概率．

变式三个标准的6面骰子被抛掷,求每个骰子正面朝上的点数至少为2且三个骰子点数之和为10的概率．

近日，意大利奢侈品牌Dolce&Gabbana（杜嘉班纳，以下简称D&G）的一则广告片因为“中式发音”、模特用奇怪的姿势使用筷子吃批萨等情景被指歧视华人。一位网友在社交媒体谈及此事时，D&G设计师Stefano Gabbana不仅不愿承认错误，反而恼羞成怒，公然辱华。

评注例1,例2分别将问题转化为排列组合中的小球分堆问题、不相邻问题,可采用隔板法、插空法解决[3]．在实际生活中,概率问题的背景各不相同,但实际蕴含的知识本质是一致的,掌握一些典型的概率模型、方法,并灵活转化问题,可促进对知识本质的理解,触类旁通,提升知识的识别、运用能力,提高解题能力．

二、对称思想

在概率的古典概型、几何概型中，基本事件是具有等可能性的,这种等可能性反映了概率中所蕴含的对称性．随机试验中,两个处于同等地位、结构一致的事件的概率相等,可运用对称性进行求解[4]．

例3一个红色的球和一个绿色的球被随机且独立地扔进一些用正整数编号的箱子里,这样对于每一个球,它被扔进垃圾箱k的概率为2-k，求红色球被扔进比绿色球更高编号的垃圾箱的概率是多少?

解红球和绿球被随机且独立扔进带有正整数编号的箱中共有可能出现三种情况:两球被扔进同一垃圾箱;红色球被扔在较高编号垃圾箱;绿色球被扔在较高编号垃圾箱．

三、方程思想

方程思想的核心体现在建模与化归,它是对现实生活中等价关系的抽象及刻画,通过数学符号建立关系式,体现了一种建模的过程,而求解方程的过程则体现了化归[5]．若概率问题直接求解较为困难,可考虑设立未知数,分析题目中的数量关系,建立已知与未知之间的等量关系,通过方程(组)进行求解．

解设c,e，m分别表示粒子从内角(如(1,1))、内部边缘(如(1,0))、中心(0,0)开始运动首次击中正方形的顶点而非侧面整点的概率．

评注粒子每次的运动方向有八种,从中心首次撞击正方形的运动路径也是多样的,带有随机性,无法一一列举,本题直接求解有困难,借助方程思想,运用乘法原理,通过设元建立粒子从不同起始位置开始首次撞击正方形顶点的概率之间的内部联系(c,e，m的关系式),省去了对粒子过程性路径的分析,大大简化了问题,思维过程也非常清晰．

四、递推思想

递推思想是数列问题延伸出的重要思想,概率问题中一些随机试验与自然数n有关,且前后两次的实验密切相关,实验过程较为复杂,可考虑运用递推的思想方法建立递推关系式,寻找初始值,将概率问题转化为递推数列的求值问题[6]．

解法1由题意可知,青蛙必落在荷叶4，7，10上,运用乘法原理,将随机事件分为三段,分别计算青蛙由0→4,4→7，7→10的概率P1,P2,P3．

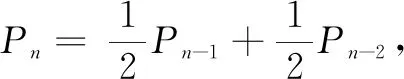
评注本题解法1是常规解法,利用乘法原理,根据题意将青蛙的运动路径划分为三段,每一段概率的计算过程实际上也蕴含了递推的思想;解法2则是直接建立出二阶递推关系式,体现了概率与数列的联系,具有一定的创新性,对于过程复杂的随机实验,这种解法更具优越性．

概率问题复杂多变,但数学思想方法是打开难题的“万能钥匙”,将数学思想方法融会贯通地运用于解题过程中会起到事半功倍的作用．概率问题中所蕴含的数学思想方法还有很多,本文所列举的四类数学思想方法在概率问题中的渗透及运用旨在带给读者一定的思考与借鉴,在实际的问题解决过程中要注重分析总结,把握其中的数学思想方法,多联想反思,提升解题能力．