巧解向量数量积问题的案例两则*

孙爱巧

(江苏省睢宁县第一中学，221200)

向量数量积常见求法有定义法、坐标法、基底法,这三种解法既相互影响,又相互渗透,既给学生解题带来了方便,也给学生带来了如何选择的苦恼.解题时只有方法选择合适,才利于消减懂而不会、会而不对的现象.前不久,一节关于向量数量积问题的习题课,学生的表现相当精彩!回味起来既有成功之处,也有欠缺的地方,现总结反思如下.

一、深层次理解定义,让“假懂”变“真懂”

案例1如图1,在ABCD中,AP⊥BD，垂足为点P且AP=3，则______.

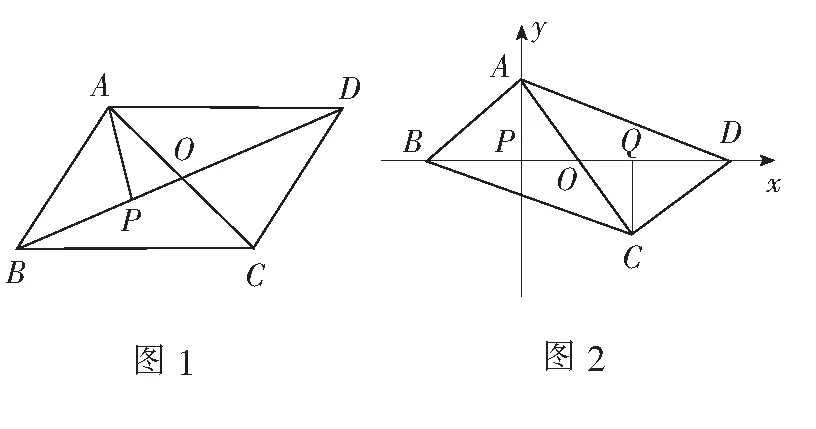
生1:(坐标法)由AP⊥BD建立如图2所示的平面直角坐标系,则A(0,3).

生2:(定义法)依题意,可得

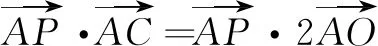
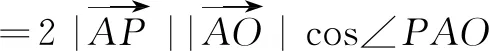
总结与反思生1的解答很巧妙,引来学生阵阵喝彩;生2的解答标准且经典,其他学生听后有一种“那么简单的问题,我怎么没想到呢”的感觉很显然,生2的解法优于生1的解答,而不少学生仍觉得生1的解法好由此可见,学生对于定义法是有所畏惧的,并非他们不“懂”定义法,而是对定义法的认识浮于表面,觉得自己“懂”了,这其实是一种假“懂”.没有从数量积的定义引申出其几何意义——两个向量的数量积等于其中一个向量的模与另一个向量在此向量上的投影之积,认识不够深刻,从而导致“懂而不会”,不能顺利用定义法解题.

二、深度剖析图形,让“做对”更高效

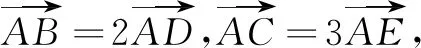
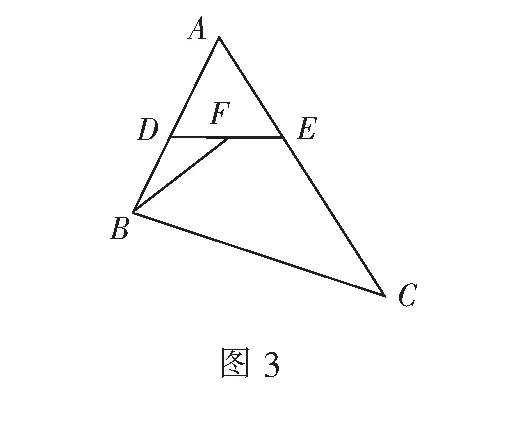
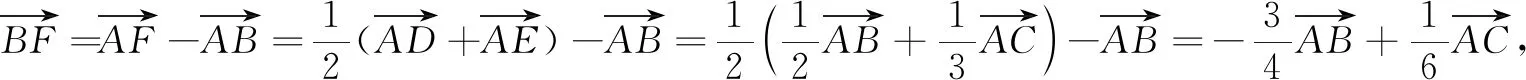
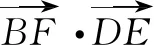
评注生3的解答代表了大多数学生的思路,但很多学生对其中大量的线性运算望而却步,虽然听懂了,甚至会做了,却没有做对的把握.

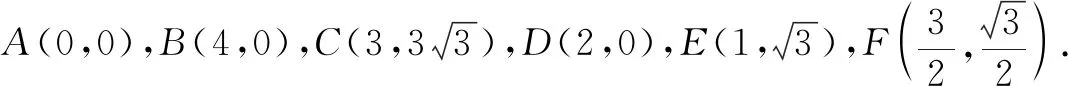
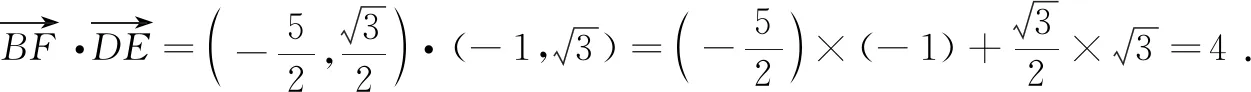
评注生4的回答又一次博得同学们的掌声,虽然此法没有生3讲的解法那么明显,但掌声代表了他们对此解法的认可.

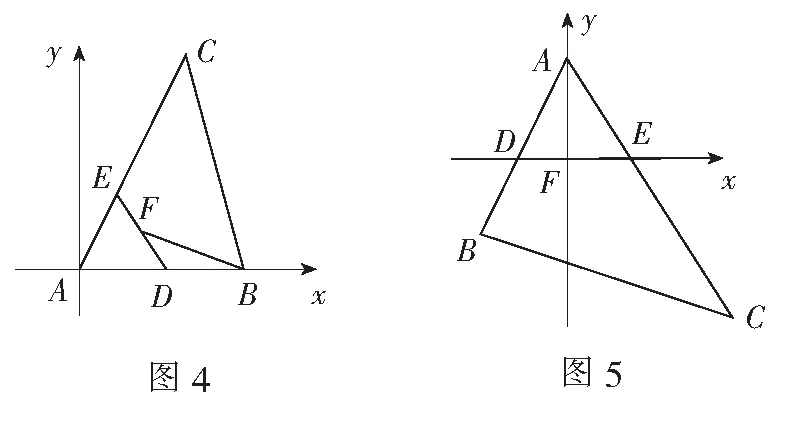
当同学们还沉浸在用新方法解决这个题目的喜悦中时,又一位学生站起来了.

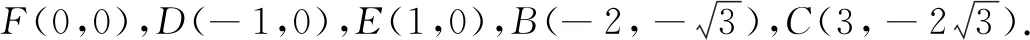
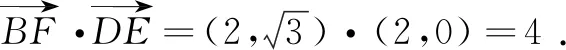
教室里掌声雷动.

总结与反思一题多解是向量数量积问题的常见形态.生3的基底法是解决数量积问题最基本的方法之一,但计算量大,对学生的基本功要求较高;生4抓住∠BAC=60°这一条件,把三角形放入平面直角坐标系,成功地把复杂的线性运算转化为简单的坐标运算;而生5对图形的理解更加透彻,同为坐标法,相比生4的解法,生5的坐标书写更简洁,计算更准确.毫无疑问,坐标法是解决向量数量积问题的一大“利器”[1],但建立坐标系前仔细研究图形,挖掘出可利用的特殊图形,化繁为简、化难为易,有利于消除“会而不对”的现象.

三、结束语

没有哪种方法是万能的!只有让学生全面分析各种解法,才能在考试中以不变应万变，这就要求教师在平时的教学中要注意以下几点.

(1)讲解知识点要全面,确保学生无知识盲区.如每学完一章,可以用“能不能写出本章的知识框架”[2]作为检验学生知识点是否掌握全面的基本标准.

(2)加强基本功的训练.数学是一门基础学科,尤其注重提高学生的运算能力和技巧,锻炼学生的思维能力.如案例2中,绝大多数学生抛弃了最常规的基底法而选择坐标法,其实是为了躲避常规的向量线性运算,这种不自信的根源,就是基本功不过硬.所以,很多学生口中的“会做”,其实是“假会”,还远远达不到“做对”这一目标.

(3)注重方法的总结和选择合适的解题方法是学生做对题目的关键.不少学生就是因方法选择不正确而走了弯路,浪费了时间,有时甚至颗粒无收.所以,教师一定要擅于解题方法的总结,引导学生总结出哪种方法可以解决哪些题型;同时也要指导学生学会优法采撷,不要盲目追求一题多解，倒是选择最基本、最合适的方法更为重要.

教无定法,教师只有在教学中多反思、多总结,才能更进一步消减学生“懂而不会,会而不对”的现象,让教师的教学如鱼得水，学生的学习轻松有效.