强制性换道的空间特征对分流区交通流的影响

钟异莹，陈 坚，邵毅明，李 睿

(1.广西科技大学机械与交通工程学院，广西柳州545006；2.重庆交通大学交通运输学院，重庆400074)

0 引 言

随着城市化进程加快，道路上机动车数量迅速增加，车辆间的作用关系越来越复杂，特别是在具有较高车流密度的主干道出口前端，部分车辆因难以提前换道至外侧车道，从而采取较为激进的换道行为，其所带来的横向干扰阻断了多车道上车辆的正常运行，通行效率受到严重影响，故研究分流区驾驶员的驾驶行为对交通流的影响尤为重要.

跟驰模型是从微观层面解释交通流演变的基础，在Bando[1]提出优化速度函数后，现有大量的、进一步的相关研究.Qi等[2]在车辆自适应巡航系统背景下，针对恒定车头时距和时变车头时距提出两种新的跟驰模型.在城市网络中，大部分道路的车道数较多，相比跟驰行为，换道行为涉及驾驶心理[3]、天气环境[4]和路段运行方式[5]等更多方面因素，对交通流的干扰程度更大.Hidas 等[6]将换道行为分为3种，即随意换道、期望换道和强制换道.针对自由换道，杨小宝[7]分析了其实施过程中车辆对前后车的影响，构建的换道模型能较好地反映车辆之间的干扰过程对交通流的影响；随后Zheng等[8]将一次换道行为划分为预期阶段和松弛阶段.相比于自由换道，强制换道大多存在于临近交叉口和上下匝道系统中[9]，极易造成交通系统的瓶颈点.现阶段研究认为，距离出口点越近则驾驶员实施强制性换道的概率越高，魏丽英等[10]的研究表明，强制性换道和自由换道常常是并存的，建立了综合换道模型.

目前的研究主要集中在双车道车辆换道过程和换道对周边交通流的影响，需进一步考虑以下问题：城市路网结构中，大部分快速路为2 车道以上，在多车道背景下，不同车道上的强制性换道行为对交通流有较大的干扰，其影响机理尚未明确；在饱和交通流情况下，驾驶员在分流区会采取不同的强制换道策略，包括激进型和保守型，有研究涉及到不同换道策略的特征[11]，Gong 等[12]将两车道分流区的强制性换道行为划分为两种，即车辆不减速实施强制性换道和车辆减速实施强制性换道，以仿真结果指导指示标牌的设置位置，但其固定了两种换道行为，没有考虑强制性换道行为的动态变化对交通流的影响.

为此，本文具体分析驾驶员强制性换道的动态决策过程，研究激进型强制换道和保守型强制换道的行为特征，提出城市快速路临近分流区时分流车辆的换道规则，将前导车减速度的动态变化作为参数与跟驰模型相结合，建立多车道下分流车辆的跟驰换道模型.仿真分析强制换道车辆的空间分布对城市主干道交通流的影响，对重构城市主干道多车道的交通流空间演变规律有一定的理论意义.

1 跟驰模型

Gipps[13]提出以安全间距为基础的跟驰模型，用于描述目标车辆可以合理选择跟驰速度，以保证在前车突然减速的情况下，能够减速并保持一定的安全距离行驶.当前车为强制换道车辆或受强制换道影响的车辆时，Gipps跟驰模型能够有效地刻画目标车辆的跟车行为，故将其运用在分流区跟驰换道模型的研究中.在Gipps跟驰模型中，x车道上车辆n的速度Vn,x(t+τ)由期望速度和维持安全距离的跟驰速度中的较小值决定，即

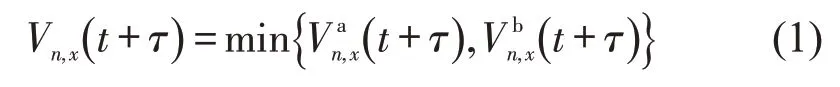
式中：t为时刻(s)；τ为驾驶员的反应时间(s)，根据文献[14]取值为1.

式中：an为车辆n的最大加速度；为t时刻x车道上车辆n所期望达到的速度；Vn,x(t)为t时刻x车道上车辆n的速度.

式中：dn为车辆n面对前车紧急制动时可能达到的最大减速度；下角标n-1 为车辆n的前车；为车辆n对前车最大减速度的估计值；gn,x为x车道上车辆n与前车的有效车头间距.

2 分流车辆的跟驰换道模型

2.1 分流区车辆强制换道策略

对于分流区的强制换道而言，驾驶员的决策行为可分为保守型和激进型两个阶段.

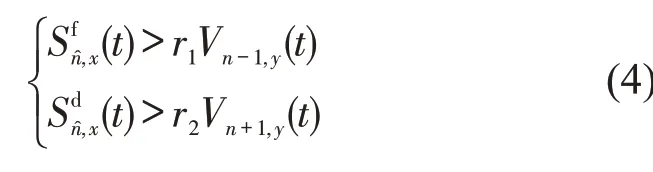
式中：下角标y为车辆的目标车道；下角标x为车辆的原车道；r1,r2分别为与y车道前车、后车的车头时距，由于存在足够距离便于车辆换道，驾驶员对侧向车道可接受间距的估计值偏大，根据文献[5]，临界值取值分别为r1=2 s，r2=2.4 s；Vn-1,y(t) 为y车道前车n-1 在t时刻的速度；Vn+1,y(t)表示y车道后车n+1 在t时刻的速度；为t时刻x车道上车辆与y车道前车的车头间距；为t时刻x车道上车辆与y车道后车的车头间距.第一阶段的换道车辆不会对侧向后车带来影响.

理想状态下，当车辆与出口的距离等于换道所需最短距离时，转入第二阶段.但在实际情况下，驾驶员通常会避免临近出口换道，Beinum等[14]指出96%的分流车辆在减速车道的中间位置开始实施换道行为，但仅针对两车道的分流区，对于多车道而言，这种心理特征在最左侧车道最为明显，驾驶员对距离的感知及需求的强烈性使激进型强制换道的起始位置(距出口的距离)在一定区间内动态变化.理论上进入第二阶段的起始位置总体上服丛正态分布，以均值um、方差σm作为特征参数，其中，m表示车道编号，激进型强制换道起始位置的概率密度函数为

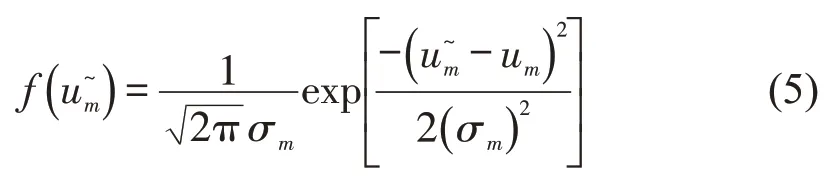
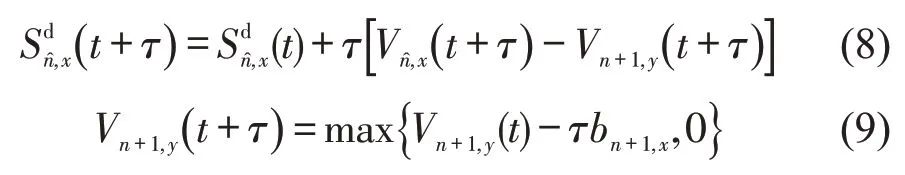
经过一段时间ΔT后，当式(6)和式(8)满足式(4)后，完成激进型强制换道进入目标车道y.

2.2 受影响车辆的跟驰行为

车辆实施激进型强制换道的过程中，不仅目标车道的后车受到影响，原车道的跟驰车辆也会受到换道车辆减速的影响，对Gipps跟驰模型中前车最大减速度进行改进，在强制换道规则的作用下设置为判断变量，即

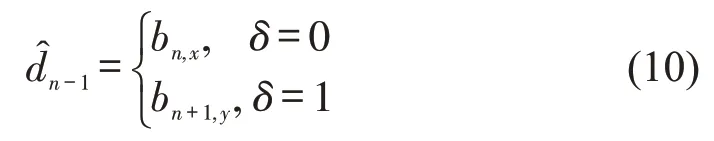
式中：δ为决策变量.当前车进行强制性换道时，δ=0，此时的前车视为换道车辆；当前车受到侧向强制换道车辆影响而减速时，δ=1，此时的前车视为换道车辆的侧向后车.

3 仿真模拟分析

3.1 模型参数标定与验证

以重庆市海峡路单向4车道为实验对象，其长为1 500 m，限速为60 km/h，车道功能如图1所示，左侧3条为直行车道，右侧为直右车道，主要流向为直行，出口位于1 200 m处.采用2018年1月6～10日的视频数据，从中选取350组强制换道时换道车辆的相关参数，以平均值标定激进型强制换道减速度bn,x=2.86 m/s2，协同换道减速度bn+1,y=3.83 m/s2，平方和误差分别为3.34%，2.52%.

图1 分流区单向4 车道路段结构示意图Fig.1 Structural diagram of one-way four-lane diverging section

为标定式(5)中um和σm，根据外侧3条车道上100 组强制性换道车辆的减速位置，采用K-S 检验，不同车道上驾驶员的激进型强制换道起始位置均符合正态分布，关键性参数如表1所示.

从表1中可以看出：车道3中激进型强制换道主要分布在出口位置(均值为438.8 m)，这与Beinum的研究相似[15]，但对于内侧车道，激进型强制换道则发生在离分流点较远的位置(均值为779.2 m)，表明不同车道数下，换道决策行为存在较大的差异.

将视频中获取的车辆到达率和各车道换道比例等基本数据作为仿真输入值，仿真步长取0.5 s，空间仿真边界为1 500 m，输出每个车道的流量与密度的仿真数据，得到4条车道的流量与密度关系图，与实际调查数据进行对比分析，结果如图2 所示.从图2 中可以看出：改进后的跟驰换道模型能够很好地模拟出每条车道交通流的变化情况，误差较低.

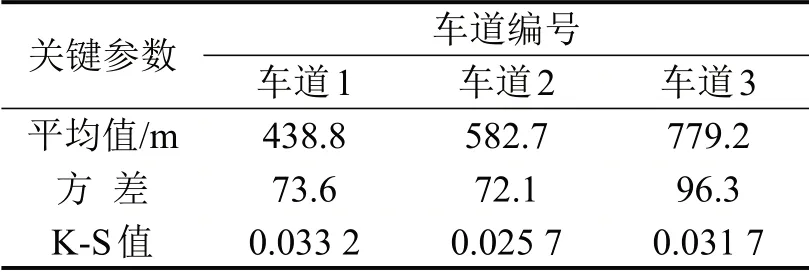
表1 概率分布函数拟合参数及检验值Table 1 Probability distribution function fitting parameters and test values

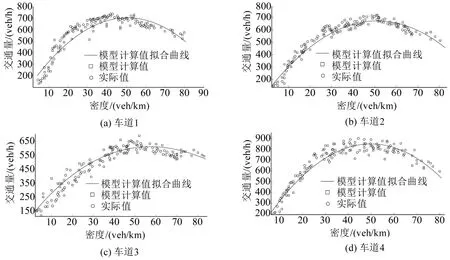
图2 仿真值与实际值对比Fig.2 Contrast of simulation value and actual data

3.2 数值仿真分析

为探讨分流车辆在不同车道上的空间分布对干道交通流运行的影响，首先设定模型中基础参数：直行方向交通需求QF=4 000 pcu/h，平均分配到每条车道，且到达率服从移位负指数分布；分流的交通需求QR初始值为800 pcu/h，分别以αm的比例存在于4 条车道，假设在高密度交通流中，只存在强制性换道，不存在自由换道.以α1=0.2 ，α2=0.5，α3=0.2，α4=0.1 为例，图3为4条车道上交通流的时空图.

从图3可以看出：车道1中激进型强制换道车辆比例较少，换道行为对目标车道干扰较小，平均速度折减量为13.6%；在多车道的道路结构中，车道3 受到的影响最为明显，大量的干扰波向后传播，达到边界的车辆明显减少，车道2 和车道3 的平均速度分别折减了27.4%和39.7%；所有换道车辆集中在车道4，但由于部分强制性换道所形成的空隙能够使多辆车同时完成换道行为，车道4的平均速度折减量小于中间两车道，为20.4%.研究结果与Gong 等[12]相似，文献[12]中的研究场景为双车道，结果表明，靠近内侧车道的车辆速度折减量大于分流车道.

图3 车辆的时空轨迹Fig.3 Time-space trajectory diagrams of vehicles

从上述分析中可以看出，激进型强制换道行为对多车道交通流的运行情况有较大的影响，进一步研究分流车辆的空间位置对交通流的干扰程度，在初始状态不变的情况下，仅针对分流车辆比例αi，设置4组实验场景，其中，车道1的分流车辆比例逐渐减少，其他车道分流车辆比例逐渐增加，实验场景的参数如表2所示.以表2中实验组为初始状态，图4为不同实验组下各车道的平均速度.

表2 4 种场景下各车道分流车辆比例Table 2 Proportion of diverging vehicles under four groups of experiments

图4 不同实验组下4 个车道的平均速度波动情况Fig.4 Average speed fluctuations of four lanes under different groups of experiments

从图4可以发现：分流车辆的空间分布对平均车速的波动有显著性影响，随着车道1中分流车辆比例增加，车道1 的平均速度虽有下降，但相比理想速度，最大衰减程度仅为24.1%，这是由于强制换道对原车道影响较小；车道2和车道3的平均速度迅速减小，波动幅度较大，相比于理想速度，两个车道在仿真时间内的平均速度最大衰弱程度分别为50.8%和51.4%；当车速达到稳定时，车道4的平均速度在4组实验中受到的影响均较小，速度的波动较为稳定，这是由于分流车辆的总数恒定，车道3强制性换道至车道4的车辆数变化不大.

值得注意的是，在实验场景4中车道1不存在分流车辆，车道2和车道3的速度波动相比于其他实验组明显较小.进一步探讨车道1分流车辆比例为0 时，分流车辆的最优空间分布，将最右侧车道上的分流车辆比例α4设定为4 种情况，分别为0.00，0.20，0.40，0.60，仿真时间设定为2 000 s，计算所有车辆运行速度平均值.为减少随机性误差，对每种情况进行10次仿真，并以10次仿真结果的平均值作为指标，图5为不同组合方案下的平均速度波动程度，其中，横坐标表示车道2 中的分流车辆比例，车道3的分流比例为α3=1-α4-α2，根据横坐标可推导出对应的分流车辆空间分布组合方案，最优组合方案如图5所示.

图5 不同组合方案的平均速度变化曲线Fig.5 Average velocity variation curves of different scheme

从图5 可以发现：当换道车辆集中在车道3时，车道1 和车道2 的平均速度不受侧向干扰，两条车道的速度稳定在理想值，但由于强制性换道造成的停车波持续累加，难以消除，只有通过车道2分担部分换道车辆，才能使整体运行速度达到最优，这也解释了图5中曲线存在先上升后下降的原因；随着车道4 分流车道的增加，速度曲线的最大值增加，波动程度减缓.

4 结 论

针对城市干道单向4车道的分流区，为完善多车道下分流车道的换道行为对交通流的影响，在强制换道模型中，通过分析保守型与激进型的特征描述驾驶员的强制换道决策行为，在此基础上优化Gipps跟驰模型中的减速度参数，建立多车道下车辆的跟驰换道模型.该方法的仿真值与实测值吻合度较高，从时空图中可以有效地描述强制性换道车辆跨越多车道对交通流的影响过程，最后探讨了换道车辆的空间分布对交通流运行速度的影响.研究结果表明，当激进型强制换道集中出现时，时空图中的停车波持续时间较长，传播距离较远；影响区域主要集中在车道2和车道3，车道4受到的影响较小；通过4组实验发现，换道车辆在4条车道中的空间分布对交通流平均运行速度的波动和衰减有显著性的影响，当分流车辆主要集中在外侧车道时，交通流整体运行速度得到提高；通过合理地控制换道车辆的空间分布可以提高交通流的整体运行速度.下一步研究中，结合驾驶员的非理性驾驶行为，考虑多出口情况下的交通流动力学特征，并以此为理论基础，给出合理的车道管理方案.