TATB 造型粉颗粒单轴压缩力学性能
马寅翔,刘 晨,王 慧,张才鑫,陈 华,张伟斌
(中国工程物理研究院化工材料研究所,四川 绵阳 621999)
1 引言
高聚物粘结炸药(polymer bonded explosive,PBX)依据成型工艺可分为压装型、浇注型、热固型等,其中压装型PBX 以其优异的性能被广泛应用。TATB造型粉颗粒一般由水悬浮法制备,结构具有多样性且差异明显[1-3],是压装型PBX 的颗粒单元,不同的颗粒结构将影响其成型PBX 的应力、变形与稳定性,因此有必要深入研究TATB 造型粉单颗粒的压缩力学性能,掌握压缩作用下颗粒尺度的结构演变,为揭示TATB 基PBX 细观结构成因及对宏观力学性能影响提供研究基础。
国内外主要通过单轴压缩加载的方式研究单颗粒的力学性能,使用Hertz 法向接触模型拟合实验获取的力-位移曲线,分析颗粒变形及颗粒强度等性能,如Russell 等[4]从能量角度考虑沸石颗粒准静态压缩变形和断裂的发生,Portnikov 等[5]通过单轴压缩力-位移曲线确定不同工业颗粒的屈服点、弹性接触刚度和有效弹性模量,Huang 等[6]利用统计方法解释玻璃球准静态压缩强度特征。上述研究虽获得颗粒的力学性能,但尚不能解释不同颗粒具有不同力学性能的原因,且研究集中在岩土与粉末技术领域的天然或工业制造的颗粒[7-11]。关于炸药造型粉颗粒尤其是TATB 造型粉颗粒力学性能的研究鲜有报道。
X 射线微层析成像(Micro-Computed Tomography,µCT)技术能以微米级别无损观测实验样品的细观特征,对于研究颗粒内部结构优势明显,已有大量工作使用µCT 技术对颗粒物质开展研究,如颗粒形态测量[12]、颗粒细观结构演化[13]、颗粒变形机理研究[14]等,但仅实现了对颗粒外形与内部结构的描述,尚未对加载过程中的颗粒力学性能进行深入研究。
本研究利用µCT 技术,设计适用于单个TATB 造型粉颗粒的压缩加载装置,原位、无损观测单个TATB造型粉颗粒单轴压缩行为,掌握其应力-位移响应与细观结构演变,获得其压缩力学性能。
2 试验与方法
2.1 试验样品
TATB 造型粉颗粒,呈黄色近球形颗粒,由中国工程物理研究院化工材料研究所制备,组成成分有TATB 粉末晶体(直径小于30 μm)、少量黏结剂与添加剂。随机选取6 颗表面基本光滑、球形度接近、粒径大小约1000~1200 µm 的造型粉颗粒,样品编号记为G1、G2、G3、G4、G5、G6。
2.2 µCT 系统与力学加载装置
用天津三英精密仪器有限公司的nanoVoxel-9010型X-μCT 系统进行CT 扫描,µCT 系统如图1 所示,主要由射线源、精密转台与带有放大镜头的探测器构成,三者的相对位置由丝杆与步进电机控制,以调整成像放大倍数。精密转台可在水平面内自由旋转、在竖直方向上升下降,探测器搭配有4,10,20 倍三种镜头实现高分辨率成像。探测器接收到来自射线源穿透样品的射线,完成一次曝光得到的射线投影图像称为数字射线照相(Digital Radiography,DR)图像,连续拍摄样品台旋转过程中的多幅DR 图像并重建被测物三维空间结构称为计算机断层扫描(Computed Tomography)成像。µCT 系统最大管电压150 kV,最大功率10 W,探测器像素数为2048×2048。

图1 µCT 系统与原位力学加载装置Fig.1 µCT scanning system and mechanical loading device
适用于µCT 系统的原位微米力学加载装置如图1所示,装置外形呈高脚杯状,使用有机玻璃材料制作。样品置于上下压头间,下压头支撑样品,上压头及上部的承载桶自重作为荷载施加于样品,承载桶内根据实验需要装入不同质量的ZrO2细沙以实现对荷载的精确控制。装置侧面有压头锁定机构,可在加载过程中随时锁定压头,限制压头位移。
TATB 造型粉颗粒受力示意如图1a 所示,颗粒受到的法向荷载F,N,表示为:

式中,m为上压头及承载桶内ZrO2细沙质量,g;g为重力加速度,9.8 mN·g-1。
2.3 CT 原位力学加载与扫描测量方法
在室温下,将单个TATB 造型粉颗粒装入加载装置,未施加荷载时上压头自重作用于造型粉颗粒,在该状态下采集颗粒的CT 图像,作为颗粒初始形态基准。随后分次将10 g ZrO2细砂倒入承载桶,并逐次拍摄DR 图像,通过对DR 图像的分析测量,获取每次加载压头压缩量/颗粒位移量。最后在颗粒发生显著变形甚至开裂崩塌的临界状态时锁死上压头并采集CT 图像。其中,DR 图片的单个像素的尺寸为1.494 μm;CT扫描像素合并数为2,CT图像的体素边长为2.988 μm。
图2 为利用DR 图像使用半峰高法的颗粒高度测量方法示意。图2a~图2d 为颗粒加载过程的DR 示例图像。在图2a 中的DR 图像最中部竖直方向取一测量线分析该线上图像灰度值变化如图2e,根据半峰高法确定不同荷载下的压头与颗粒接触边界,进而得到颗粒高度,对每次加载得到的DR 图像进行颗粒高度测量,获得加载过程的位移信息。位移测量最大误差为1 个像素即1.494 μm,实际测量中定位半峰高位置所在的像素可根据灰度值-坐标曲线精确到亚像素级别。
图3 为将TATB 造型粉颗粒等效为椭球体的方法,计算方法如式(2)所示。该方法以颗粒高度与横截面参数,将造型粉颗粒外形等效为一个具有两根等长长轴与一根短轴的椭球体。
颗粒与压头的接触半径RC可表示为椭球体在顶点处的曲率半径,μm,即

式中,HH为颗粒的半高度,μm,定义为颗粒未加载初始状态高度的一半。Req为横截面等效半径,μm,定义为与颗粒半高度位置横截面面积相同的正圆的半径。颗粒放置在压头位置的纵横比AR为

图2 造型粉颗粒加载过程DR 图像序列与压头距离测量方法示例Fig.2 Sequence of DR images of granule under different loading and approach of indenter distance measurement

图3 造型粉颗粒等效为椭球体方法Fig.3 The method of equivalent transformation of granule to ellipsoid

3 结果与讨论
3.1 颗粒特征CT 扫描结果
图4 为未加载状态TATB 造型粉颗粒CT 扫描结果,第一列为颗粒三维重建图,后三列为颗粒中间位置xy、xz与yz截面切片。从图4 可以看出:颗粒近似球形,表面存在凹坑凸起等特征,G1 与压头的接触面有小的凸起,G6 与压头的接触面有较为明显的大凸起,且G1~G6 均有高密度致密表层;G5 尺寸相对最小,G6 球形度最差;G1 内部孔隙少,呈小片状,G2 内部孔隙少且分散,G3 中心连通的孔隙较大,G4 孔隙相对密集,G5 有“C 字形”片状孔隙,G6 有平行于加载方向的片状连通孔隙。颗粒内部结构有明显差异。
表1 为结合DR 图像与CT 切片图像得到TATB 造型粉颗粒的横截面等效半径、颗粒半高度、接触面半径、纵横比、接触面形貌、颗粒内部缺陷形貌等特征。结果显示:G1~G5 颗粒纵横比小于1,呈扁球状,G6颗粒纵横比大于1,形状较为不规则。
3.2 颗粒压缩力学性能分析
3.2.1 颗粒受力-位移曲线
图5 为TATB 造型粉颗粒准静态单轴压缩实验的受力-位移曲线。可以看出,最后一次加载产生的位移明显大于之前数次加载的位移。结合DR 实验观察,最后加载点造型粉颗粒失去承载能力,发生破坏崩塌,因此本研究认为每条曲线的最后2 个数据点分别为破坏点和崩塌点。此外,颗粒力-位移曲线表现出明显的阶段特征,与压头接触的初始阶段,曲线斜率(代表刚度)较大,中间段斜率下降,最后阶段颗粒破坏,曲线斜率接近0。
3.2.2 颗粒压缩变形过程
3.2.2.1 弹性变形阶段
Hertz 法向接触模型[15]确定了颗粒受法向力准静态压缩变形时的荷载、位移、杨氏模量和泊松比等的关系,模型适用于各向同性弹性固体球间非粘正压小变形弹性接触的情况,在某些微凸颗粒、内部非完全均匀的颗粒也被证明有良好的适用性[16-19],有效性得到广泛认可[20]。Hertz 法向接触模型给出了准静态压缩弹性球体的力-位移关系:
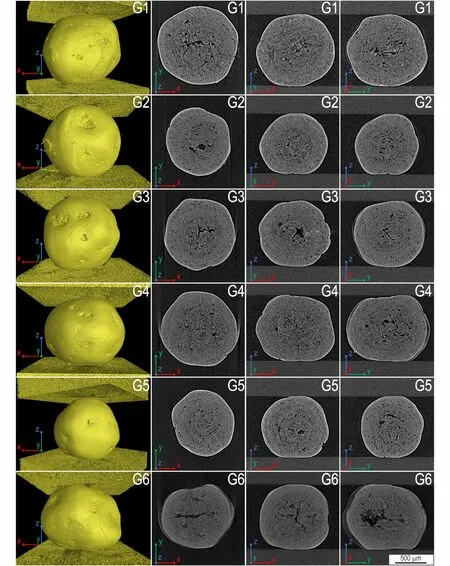
图4 TATB 造型粉颗粒未加载状态CT 扫描结果Fig.4 CT scan results of TATB granules before loading
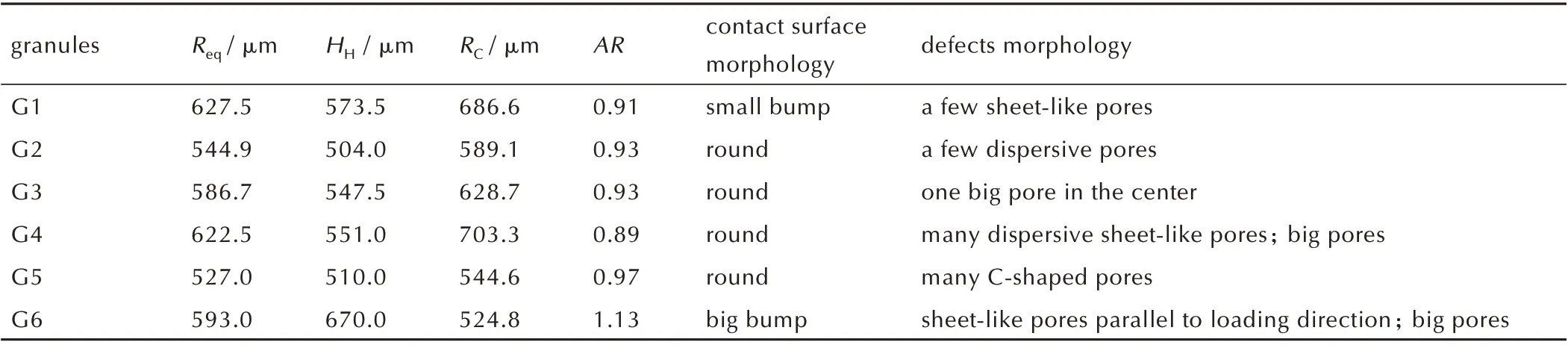
表1 TATB 造型粉颗粒结构特征Table 1 Characteristics of TATB granules
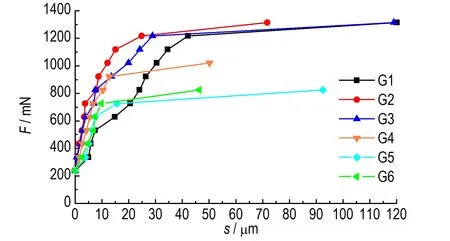
图5 TATB 造型粉颗粒加载力-位移曲线Fig.5 Force-displacement curve of TATB granules
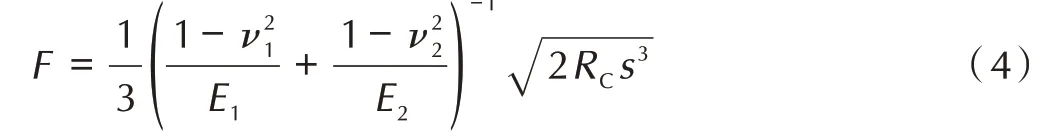
式中,F为弹性变形阶段的压缩荷载,mN;s为压头位移,μm;E1,E2分别为TATB 造型粉颗粒与压头的杨氏模量,GPa;ν1,ν2分别为TATB 造型粉颗粒与压头的泊松比;RC为TATB 造型粉颗粒与压头接触位置的接触半径。本实验中,上压头预先加载稳固颗粒,再开始加载记录数据,因此初始位移为0,荷载为上压头自重,故对Hertz 法向接触模型公式(4)作如下修正:
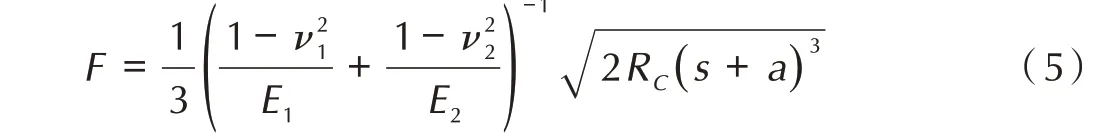
其中,a为常数,物理意义为预加载的上压头重量作用在颗粒上使颗粒产生变形的位移大小,由对力-位移曲线的Hertz 法向接触模型拟合结果确定。所用TATB材料泊松比约为0.3[21],经测定,所用压头材料泊松比ν1约为0.35,压头杨氏模量E2为3.73 GPa。
使用Hertz 法向接触模型对G2~G6 颗粒力-位移曲线拟合如图6。
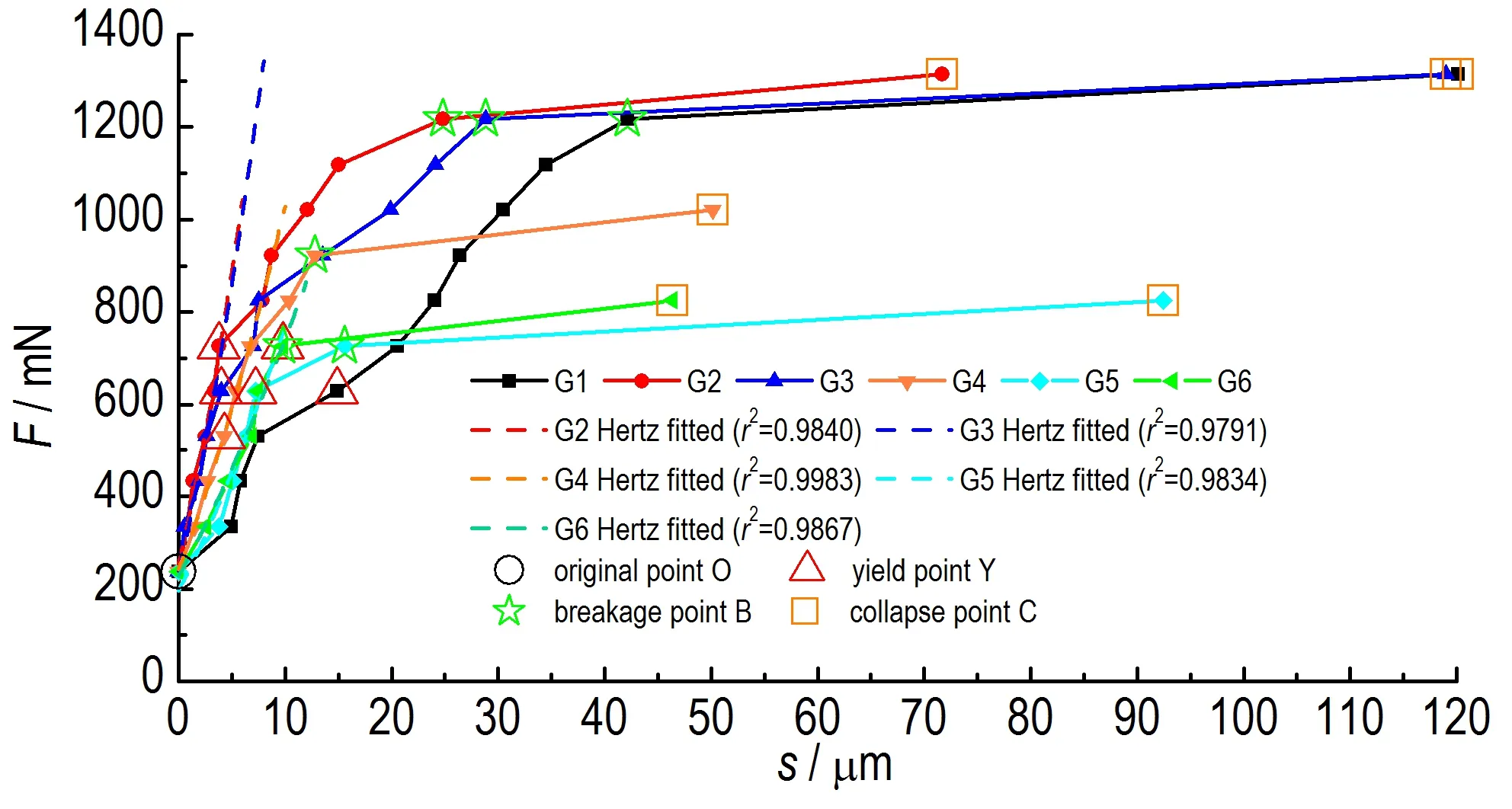
图6 TATB 造型粉颗粒加载力-位移曲线的弹性阶段Hertz 拟合Fig.6 Elastic Hertz fitted of force-displacement curve for TATB granules
在Y点之后拟合的Hertz 法向接触模型曲线与实验数据发生偏离,偏离的位置Y点为屈服点,即OY 段对应弹性变形阶段,Y点之后颗粒开始发生塑性变形刚度变低。屈服点Y处Hertz 拟合曲线的斜率即屈服点处的接触刚度kY,mN·μm-1:

式中,SY为屈服点处颗粒变形量。屈服点处的变形率ψY表示为压头位移与造型粉颗粒竖直高度的比值:

图6 可 以 看 出,G2~G6 颗 粒 拟 合 系 数r2大 于0.9791,弹性变形变形率约为5.7‰。
弹性变形阶段变形主要由压头与颗粒接触的颗粒最顶端凸起位置承担,随着荷载的增大,颗粒与压头接触面积逐渐增大,刚度也逐渐增大。颗粒与压头接触的表面形貌在一定程度上影响弹性变形阶段的力-位移关系。图7 展示了G1 颗粒与压头接触的上下表面CT 三维重建图,发现接触面较不平整,尤其是与上压头接触的上顶面存在凹坑与凸起,光滑度与圆度差,当荷载逐渐增大时,接触面上的凸起部分先后发生弹性变形至塑性屈服,凸起位置局部符合Hertz 法向接触模型,但多个凸起变形过程叠加后,力-位移关系曲线整体表现无规律,因此G1 颗粒的力位移关系不符合Hertz 法向接触模型,该颗粒“弹性”段结束(即弹-塑性阶段开始)的位置的变形率达到13‰,远高于G2~G6颗粒的3.6‰~7.1‰,说明该颗粒在初始变形阶段由于接触位置的凸起部分先后的局部弹性或塑性变形产生的位移发生累积。
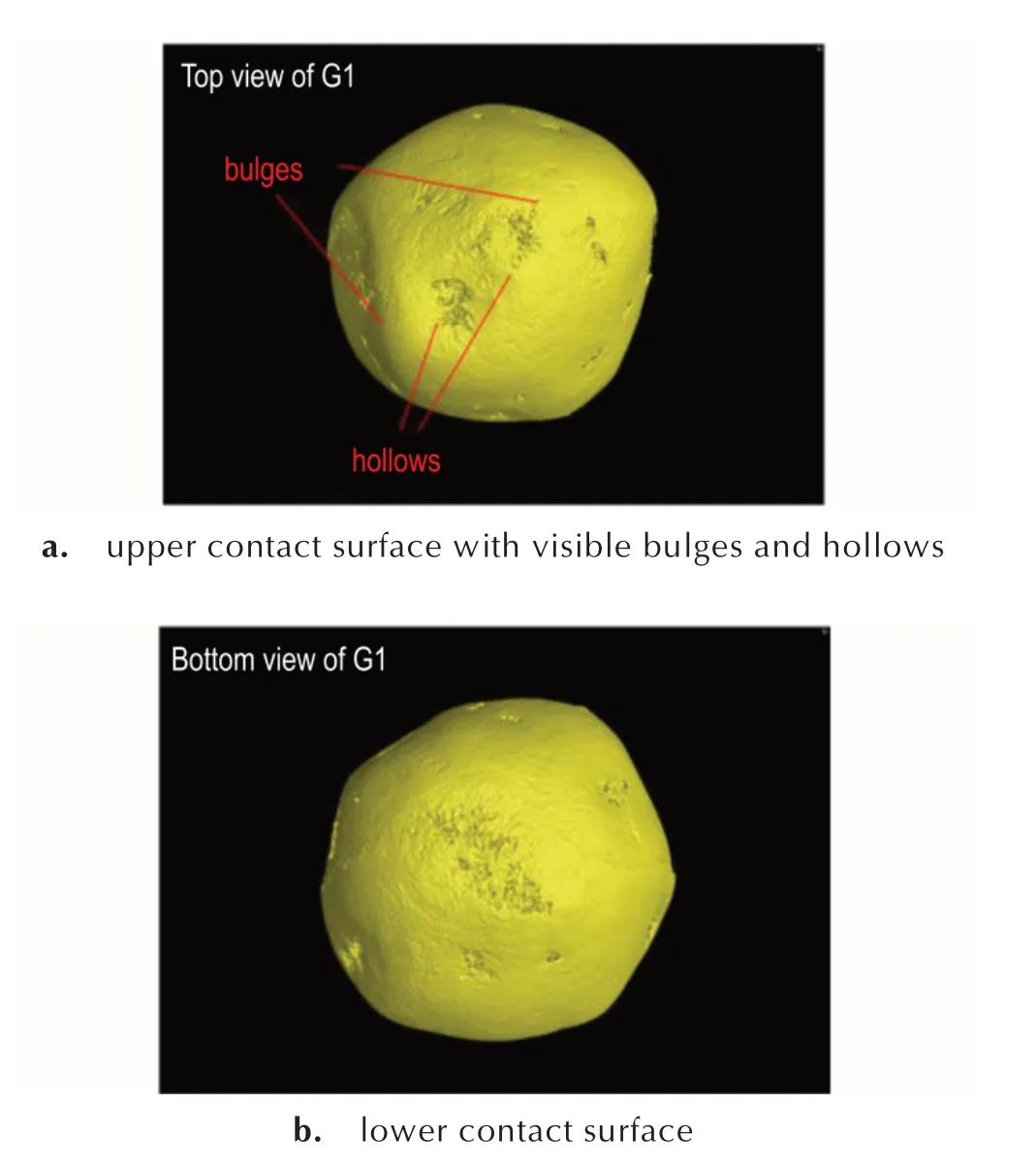
图7 G1 颗粒CT 三维重建图Fig.7 Three-dimensional CT reconstruction of G1 granule
3.2.2.2 弹-塑性变形阶段
颗粒所受荷载大于屈服点Y 的屈服荷载之后,颗粒内部应力超过其弹性极限,发生塑性变形。这一阶段颗粒内部同时发生各占一定比例的弹性与塑性变形,称这一阶段为TATB 颗粒的弹-塑性变形阶段。该段力-位移曲线较前段斜率明显下降。
经实验发现,虽然造型粉颗粒内部结构各不相同,但在弹-塑性段力-位移曲线总体表现线性。对G1~G4 颗粒弹-塑性变形阶段YB 曲线的线性拟合(拟合系数r2>0.8747)如图8 所示。虽然造型粉颗粒内部结构各不相同,但从图8 线性拟合结果及文献[5,7-9,11]等中可发现弹-塑性段力-位移曲线总体表现线性。拟合的直线斜率代表弹-塑性阶段有效接触刚度kel-pl,mN·μm-1。G5 颗粒弹塑性段仅有两个数据点,未做拟合,G6 颗粒力-位移曲线没有表现出明显的弹-塑性段特征。
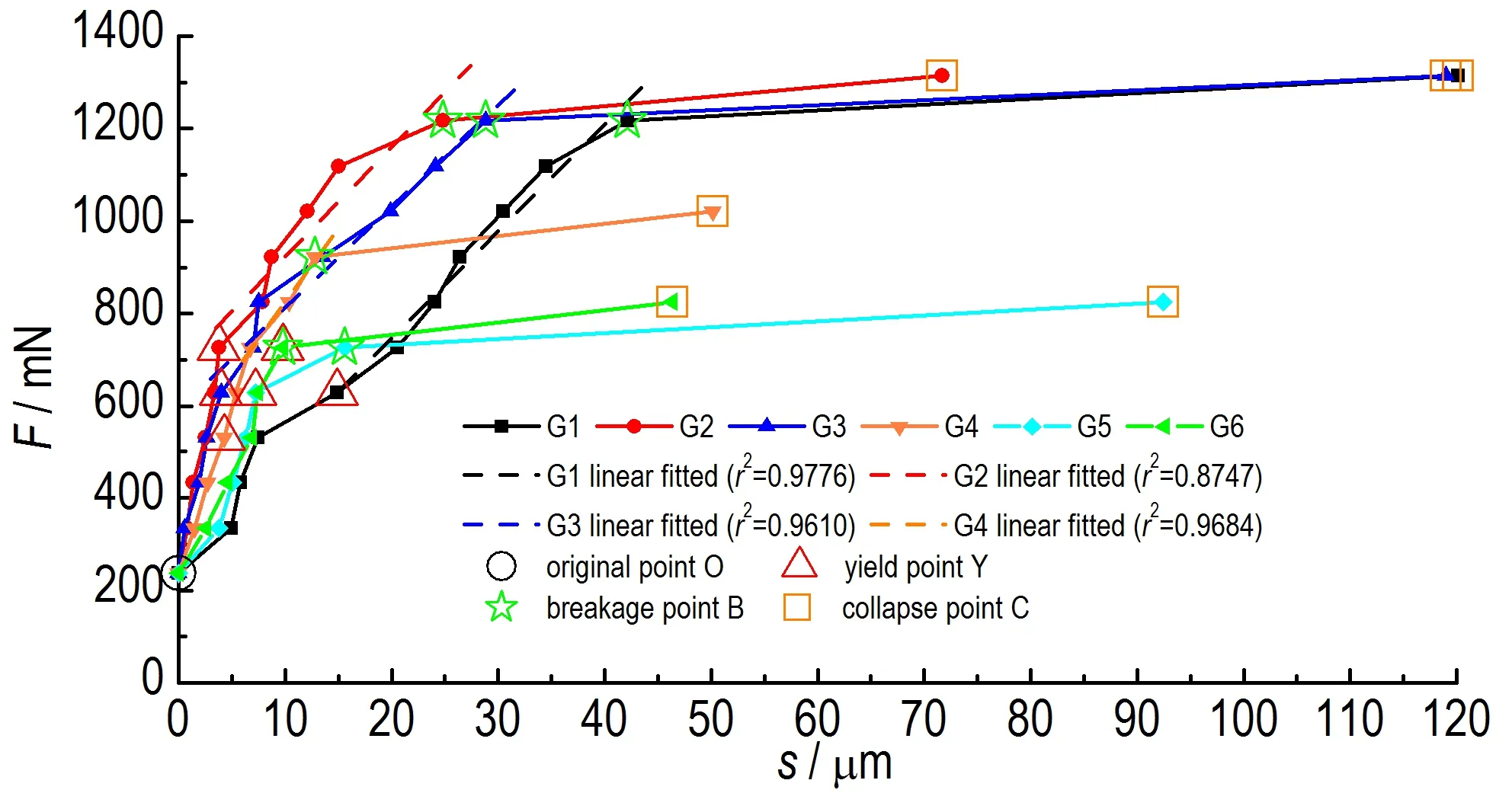
图8 TATB 造型粉颗粒加载力-位移曲线弹-塑性阶段线性拟合Fig.8 Elastic-plastic stage linear fitted of force-displacement curve for TATB granules
当颗粒变形达到一定程度时(B点),颗粒发生开裂,失去承载能力。特征破坏强度σB可从破坏荷载与垂直于加载方向最大横截面面积的比值确定:

式中,sB为破坏点处颗粒变形量,μm。
G4~G6 颗粒破坏过程发生迅速,未采集到破坏时CT 图像,G1 颗粒在初始弹性阶段力位移曲线不符合典型的Hertz 模型规律,这里以G2、G3 颗粒为例,分析TATB 造型粉颗粒变形破坏内部结构变化。图9 为G2、G3 两颗造型粉颗粒在图8 破坏点B点的CT 重建图及三正交截面CT 切片图,相比图4 中未加载状态,发现G2、G3 颗粒内部缺陷尺寸小且空间分散或远离颗粒表面,在颗粒受载经历弹性阶段变形、弹-塑性阶段变形直至开裂过程中,内部小缺陷结构对造型粉颗粒整体强度影响不大,内部缺陷仅发生很少扩展,具体体现为垂直于加载方向的横截面xy的拉张变形诱发原有缺陷扩展或是连通;平行于加载方向的横截面yz与xz切片反映出内部初始缺陷直到破坏时都仅发生极小扩展。压头运动产生的颗粒发生明显变形位置主要在颗粒与压头接触的弧面,即颗粒被粘结剂包覆的高密度致密表层。
图8 可以看出,G4~G6 颗粒破坏过程发生迅速,弹塑性段几乎不可见。而且图4 的G4、G5 与G6 颗粒未加载初始状态的CT 切片图像观察到,G4~G6 颗粒内部缺陷偏大、较多且有长条形平行于加载方向的连通孔隙,推测这些平行于加载方向的大孔隙缺陷在颗粒压缩时膨胀,进而导致颗粒开裂、失去承载能力、破坏并崩塌。由于内部较大缺陷的存在,G4 与G5 颗粒的屈服荷载与特征破坏强度明显低于其他颗粒,尤其在颗粒变形进入弹-塑性阶段时,颗粒承载能力显著下降。G6 颗粒弹-塑性段几乎不可见,没有明显的屈服点,其内部平行于加载方向的片状孔很快扩展,并导致了G6 颗粒在被测样品中具有最小的杨氏模量、刚度、特征破坏强度等性能。

图9 G2 与G3 颗粒破坏点B 点的CT 扫描结果Fig.9 CT scan results of G2 and G3 granules at breakage point B
3.2.2.3 破坏崩塌阶段
破坏点B 后的加载导致颗粒发生崩塌,图6 曲线中BC 段发生远大于之前变形的位移,崩塌点C 处的变形率记为ψC:

式中,sC为崩塌点颗粒变形量,μm。
图10 展示了G3 颗粒在崩塌点C 采集的CT 重建图像与三正交截面的CT 切片图。颗粒崩塌是内部结构的开裂变形,相对崩塌前的状态有明显位移,崩塌过程比破坏过程内部变形程度更大,存在许多贯穿颗粒的裂纹。大规模的破裂增加顶部和底部接触区域的接触面积,减小应力集中,同时颗粒受压沿着竖直方向劈开成多个部分,这几部分碎块围绕中心碎片环绕分布。

图10 G3 颗粒崩塌点C 点的CT 扫描结果Fig.10 CT scan results of G3 granule at collapse point C
3.2.3 颗粒压缩力学性能
根据式(4),(10)计算得出TATB 造型粉颗粒弹性阶段的杨氏模量、屈服点刚度、屈服荷载、屈服点变形率、弹-塑性阶段的刚度、破坏荷载、破坏强度、破坏点变形率、崩塌阶段的崩塌荷载、崩塌点变形率等,压缩力学性能如表2 所示,表2 显示出,G1~G6 颗粒压缩力学性能有明显差异,主要原因可能由G1~G6 内部结构的明显差异所致。

表2 TATB 造型粉颗粒压缩力学性能Table 2 Mechanical properties of TATB granules by compression
4 结论
通过设计的适用于单个TATB 造型粉颗粒的压缩加载装置,利用µCT 技术原位、无损观测单个TATB 造型粉颗粒单轴压缩行为,得出结论如下:
(1)测得的颗粒杨氏模量约为0.98~8.74 GPa,屈服点接触刚度约为60~140 mN·μm-1屈服点变形率约为3.6‰~7.1‰,弹-塑性段刚度约为11.7~31.8 mN·μm-1,特征破坏强度约为0.73~1.36 MPa。
(2)与压头接触的颗粒表面情况对弹性变形阶段影响最大。对于内部缺陷较大较多的颗粒,尤其是平行于加载方向的片状孔隙,缺陷对弹-塑性变形阶段影响较大,缩短了弹-塑性变形阶段过程,显著降低了破坏强度与破坏变形率。对于内部缺陷较少且分散的颗粒,从初始状态至破坏失效过程中,颗粒内部结构及缺陷没有显著变化,小缺陷对颗粒力学性能的影响不明显。

