基于有限元-离散元结合方法的Steven 实验三维数值模拟

黄彬彬，傅 华，喻 寅，刘仓理

（中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621900）

1 引言

炸药在跌落、翻倒等低速撞击事故中易经受低幅值（数十到数百兆帕）、长脉冲（数百微秒）的非冲击载荷，可能造成炸药发生意外点火，引发安全性事故。但炸药非冲击点火的实验精细观测存在多方面的困难与限制，不易获得点火演化的细节与机制。因此，开展非冲击点火的数值模拟研究，对深入揭示炸药在低速撞击下的响应规律具有重要意义。

Chidester 等［1-3］设 计 了Steven 实 验 用 于 研 究 带壳体约束的炸药经受低速撞击下的非冲击点火问题，建立了撞击点火模型并采用实验获得的临界撞击速度对模型参数进行标定。此后，众多国内外学者开展了相应的数值模拟工作，分析了不同形状弹头加载下的点火速度阈值和点火位置等［4-7］。目前相关的数值模拟工作主要采用了有限元方法与离散元方法。其中有限元方法（Finite Element Method，FEM）具有高精度、高效率等优点，是目前最成熟且应用最广泛的力学响应计算方法，但是依赖网格的计算方法普遍存在不适合模拟大变形和损伤断裂现象的缺点，虽然基于微裂纹界面的摩擦生热的点火模型（Visco-SCRAM 模型）在炸药低速撞击点火数值模拟中也有较多应用［8-11］，但在处理撞击加载下炸药局域点火前的压剪断裂与断裂之后的裂纹摩擦等非连续性问题时还是面临较大的困难。离散元方法（Discrete Element Method，DEM）的基本思想是把不连续体或连续体离散为具有一定物理意义的独立“微元”或“粒子”，粒子间通过虚弹簧保持连接，粒子间的相互作用力通过弹簧的拉伸和压缩来实现，因此在处理断裂和破碎问题时具有天然优势，目前也被广泛应用于炸药力学响应机理的模拟研究［12-18］，但是由于离散元不擅长描述材料的塑性变形，同时出于计算尺度和效率的考量，在应用于炸药材料模拟时，通常模拟中未考虑炸药外部的金属壳体对其非冲击点火行为的影响。

本研究中建立了有限元-离散元结合方法，利用有限元模拟装药结构响应，利用离散元描述炸药局部断裂损伤，针对脆性炸药PBX-2 的Steven 实验开展了三维数值模拟，获得了装药受载应力历史、裂纹分布、温升曲线及温度分布。以炸药裂纹摩擦以及自反应放热为主导点火机制，分析了由炸药材料非均质特性引起的的概率点火现象，并讨论了钝头弹与平头弹撞击下点火位置的分布特性。

2 计算方法及模型

2.1 FEM-DEM 结合方法

FEM-DEM 结合方法的核心问题在于有限元单元与离散元粒子间接触作用力的计算。由于离散元单元本身具有一定尺寸，区别于有限元节点仅仅是一个点，因此离散元粒子-有限元面单元的接触可以根据其接触位置的不同分为三类，即：粒子-表面（Paticles-to-Facets，简称PTF）、粒子-棱边（Paticles-to-Edges，简称PTE）、粒子-顶点（Paticles-to-Vertices，简称PTV），如图1所示。

三种接触方式下的离散元单元所受到的作用力为；

式中，κ为自定义接触系数；δn为侵彻距离，m；n为单位法向量；E*为等效杨氏模量，MPa；r*为等效半径，m；k法向刚度，N·m-1。

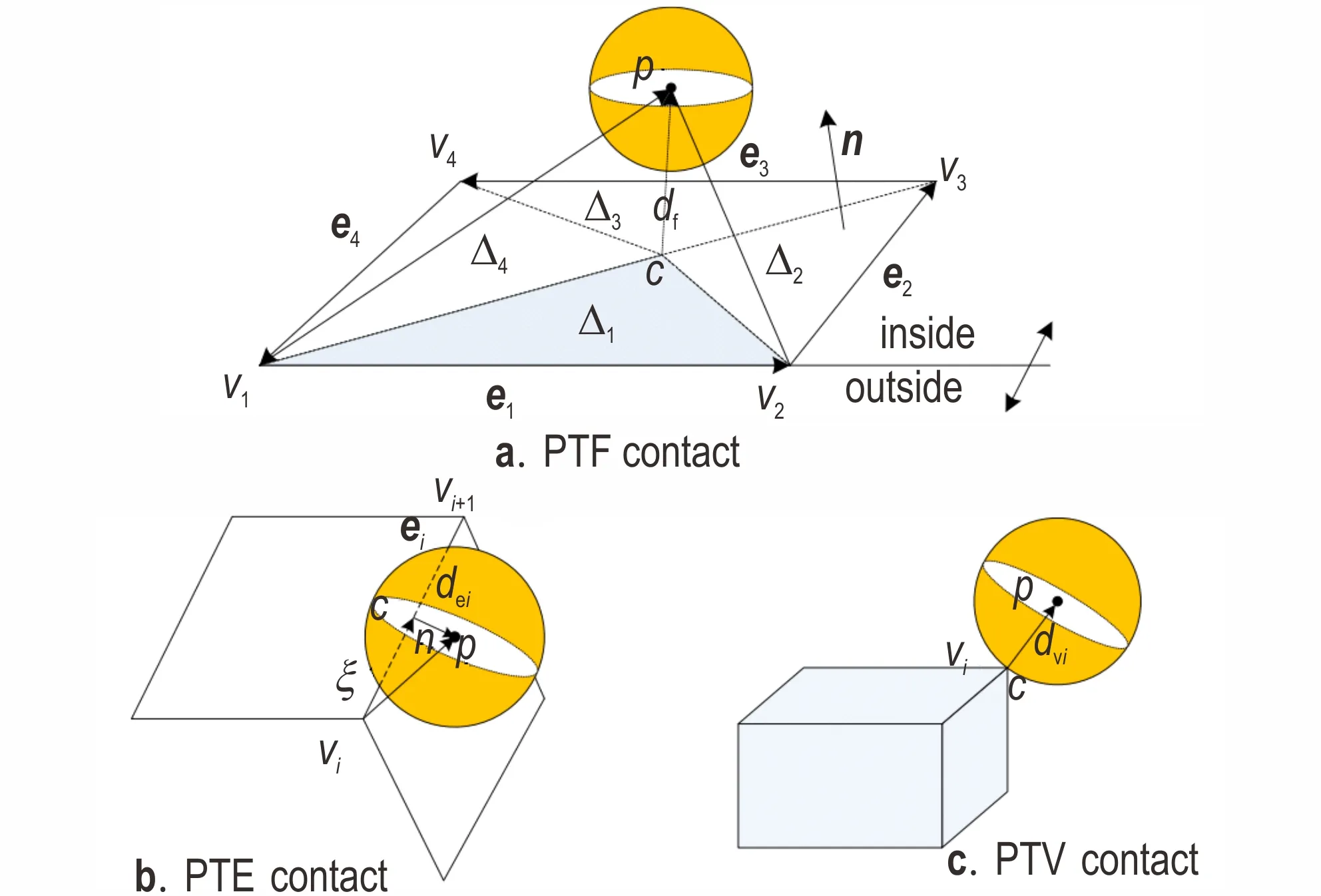
图1 离散元单元与有限元面单元接触模型Fig.1 Contact model between a discrete-element particle and a finite-element facet unit

2.2 DEM 断裂模型

PBX-2 各组分的质量百分比为HMX/TATB/黏结剂+钝感剂=87/7/6，属于典型的脆性炸药，因此采用弹脆性本构对其进行描述。假设材料为各向同性，建立的离散元模型如图2 所示，图2a 为球形离散元结构示意图，图2b 为相邻单元间作用力示意图。

图2 离散元模型示意图Fig.2 Schematic diagram of discrete-element model

当两个处于连接状态的离散元单元间法向作用力fn与切向作用力fs满足关系式（5）中关系时，则判定其连接断裂，两个单元由连接状态变为接触状态：

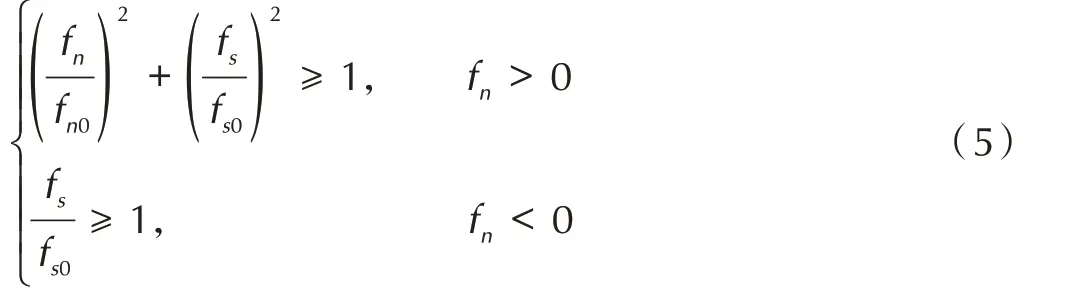
式中，fn0和fs0分别为定义的最大法向与切向作用力，N。

为验证该计算方法以及所选取模型的有效性，对脆性炸药PBX-2 的分离式霍普金森杆实验（SHPB）进行了数值模拟。模型包含炸药试样、子弹、整形器、入射杆和透射杆，炸药试样尺寸为φ12 mm×6 mm，子弹尺寸为φ20 mm×300 mm，入射杆尺寸为φ20 mm×2000 mm，透射杆尺寸为φ20 mm×1000 mm。炸药试样采用离散元划分网格，半径为125 μm，其余部分采用有限元划分网格，网格尺寸为2 mm，如图3 所示。分别于A、B、C三点处记录入射波、反射波和透射波信息。

“民营企业反映突出的痛点、难点、堵点，给出了6方面35条政策,让我们真正从政策中增强获得感。”记者在采访谢清森时，他用这句话表达自己内心的最大感受。

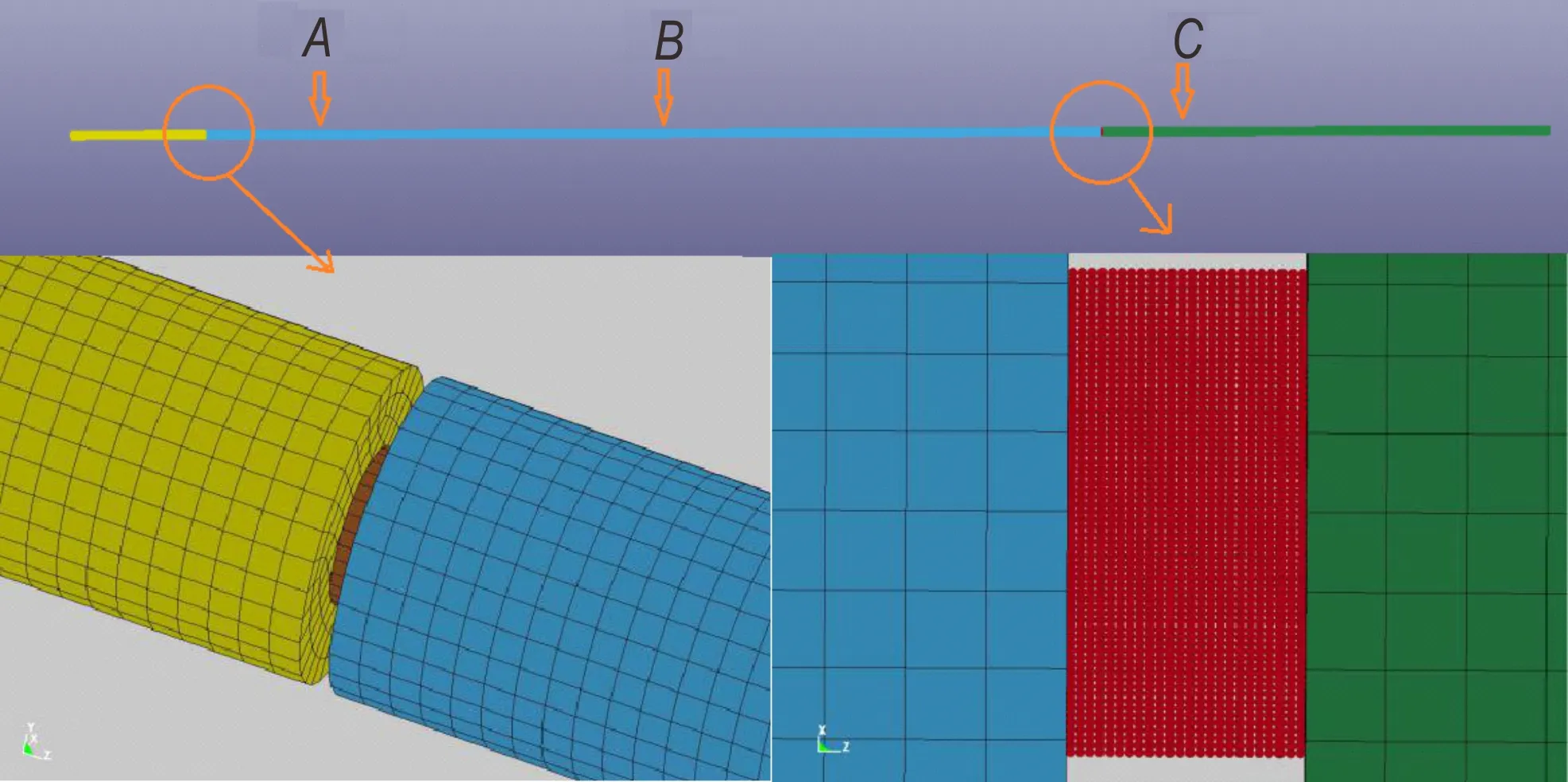
图3 SHPB 实验计算模型Fig.3 Calculated model of SHPB test

计算模型中采用弹脆性本构，弹性段弹性模量E=5.5 GPa，平均断裂应变ε=0.01。模拟结果与实验结果对比如图4 所示。从图4a中可以看出，计算得到的三波（入射波、透射波、反射波）波形与实验结果符合较好，表明该计算方法能较好地处理FEM-DEM 接触界面间的物理量传递。图4b中应力-应变本构关系模拟结果与实验结果大致吻合，呈现明显的弹脆性特征，表明所采用的断裂模型适用于模拟脆性炸药材料的力学响应。

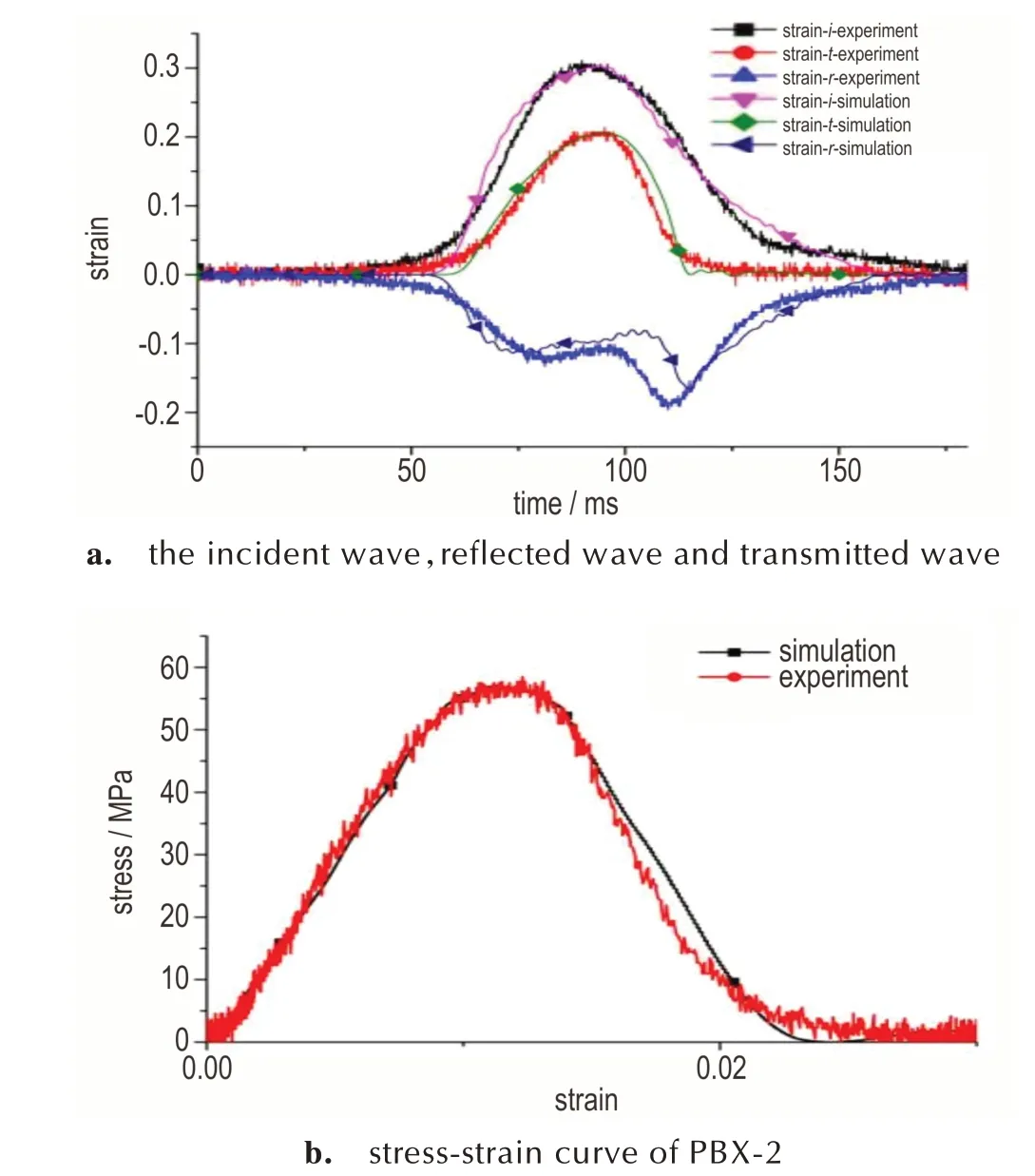
图4 SHPB 实验模拟结果Fig.4 Simulation results of SHPB experiment

2.3 温升点火模型

考虑到相比炸药塑性功产生的热量，颗粒间的摩擦温升更容易产生较高的局部温升导致点火，因此主要计算炸药断裂后的摩擦生热以及炸药自反应放热作为热源。

两个接触的离散元粒子i与j之间的摩擦力可表示为：

式中，eij为耗散能量，J；Δt为时间步长，s。

由于加载过程为瞬态过程，一个时间步长内单元间相互作用可视为绝热过程，则粒子i的摩擦温升为：

采用Arrhenius 方程［17］描述炸药自反应放热

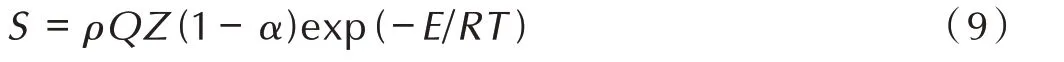
式中，S为源项，J∙s-1；ρ为炸药密度，g∙cm-3；Q为反应热，J∙kg-1；Z为指前因子，s-1；E为活化能，J∙mol-1；R为普适气体常数，8.314 J∙mol-1∙K-1；T为温度，K；α 为已反应炸药分数。初始温度设为298 K，炸药反应动力学参数见表1［18］。

表1 PBX-2 炸药反应动力学参数［18］Table 1 Kinetic parameters of explosive reaction for PBX-2［18］

当某个炸药单元的温度超过某个临界温度，根据Arrhenius 方程，将大量放热导致温度近乎直线上升超过3000 K，这种情况下我们可以判定炸药发生了点火。因此，可以将温度出现快速上升的拐点作为点火临界点，其对应的温度为点火临界温度。

2.4 Steven 实验计算模型

模型包含炸药试样、盖板、约束环、样品盒和弹丸。炸药试样尺寸为Φ98 mm×13 mm，压板尺寸为Φ120 mm×3.5 mm，样品盒底部高度19 mm，弹丸主体部分半径为31 mm。炸药试样采用离散元划分网格（半径400 μm），其余部分采用有限元划分网格（网格尺寸4 mm），建立的FEM-DEM 模型如图5 所示。

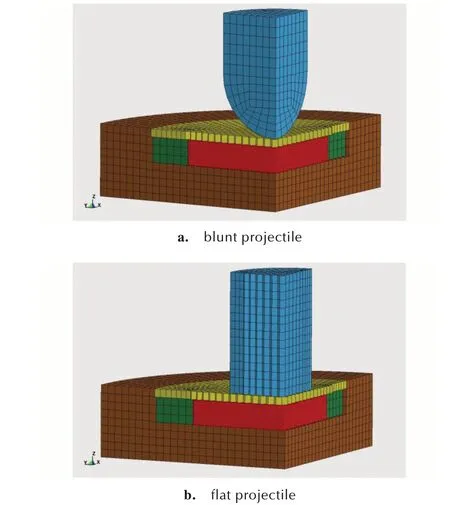
图5 不同形状弹头Steven 实验计算模型Fig.5 Calculated model of Steven impact test for different projectile heads

模型中所用样品为PBX-2 炸药，弹丸、盖板和样品盒的材料为Q235 钢，约束环材料为聚四氟乙烯，模型中各材料性能参数见表2［18］。

实际加载中，炸药材料的孔洞坍缩、炸药-粘结剂脱粘等行为会进一步导致响应局域化，因此模型中需要考虑炸药材料的非均匀性。为模拟炸药材料的非均匀性，选取随机分布的占比为1%的离散元单元，设置其最大法向与切向作用力为其余单元的一半。

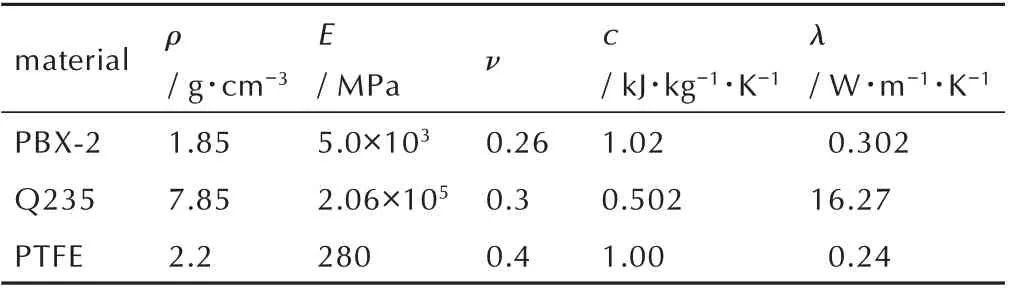
表2 模型中各材料性能参数Table 2 Performance parameters for various materials in the model

3 结果与讨论

3.1 力学响应与损伤裂纹

采用有限元/离散元结合方法得到钝头弹在撞击速度为45 m·s-1时炸药样品底部中心处压力的模拟结果，将其与文献［15］实测曲线进行对比，如图6 所示。由图6 可以看出，试样底部中心处的压力峰值约为0.10 GPa。弹丸撞击后压力迅速升高，在约170 μs 处达到峰值，之后随弹丸反弹压力持续下降，进入卸载阶段，卸载阶段持续380 μs 左右。数值模拟的压力峰值及压力脉冲宽度都与实验测试曲线符合较好，表明该方法能较准确地模拟Steven 实验中炸药的受力过程。

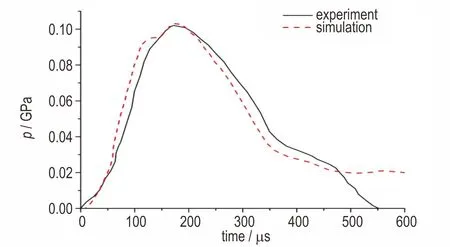
图6 炸药底部中心实测和计算压力曲线（钝头弹弹速45 m·s-1）Fig.6 Experimental and simulated pressures at the bottom center of explosives（the velocity of blunt projectile is 45 m·s-1）

图7 和图8 为不同弹丸撞击下炸药试样内部产生的力学响应及损伤裂纹分布情况。在钝头弹实验中，裂纹由弹头轴线处沿径向发散，形成多段贯穿裂纹（图7a 和图7b）；在平头弹实验中，裂纹沿弹头圆周附近呈环状分布（图7c 和图7d）。对比图8 中的应力分布情况可知，装药试样受到钝头弹撞击后，撞击中心的炸药受到弹丸挤压（图7a），该区域的炸药向远离撞击中心的方向运动，应力最大值始终集中于轴线附近（图7b）；装药试样受到平头弹撞击后，在弹头边缘与盖板接触处发生强烈的剪切作用（图7c），从而形成绕圆周分布的损伤裂纹，而弹头下方的炸药在轴向被压实（图7d）的同时也会产生较分散的损伤裂纹。

3.2 点火阈值与点火位置

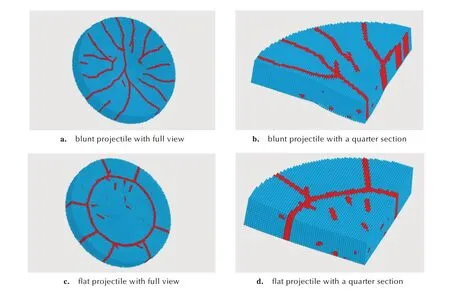
图7 不同形状弹头撞击下PBX-2 炸药的裂纹分布Fig7 Crack distribution of PBX-2 under the impact of different projectile heads

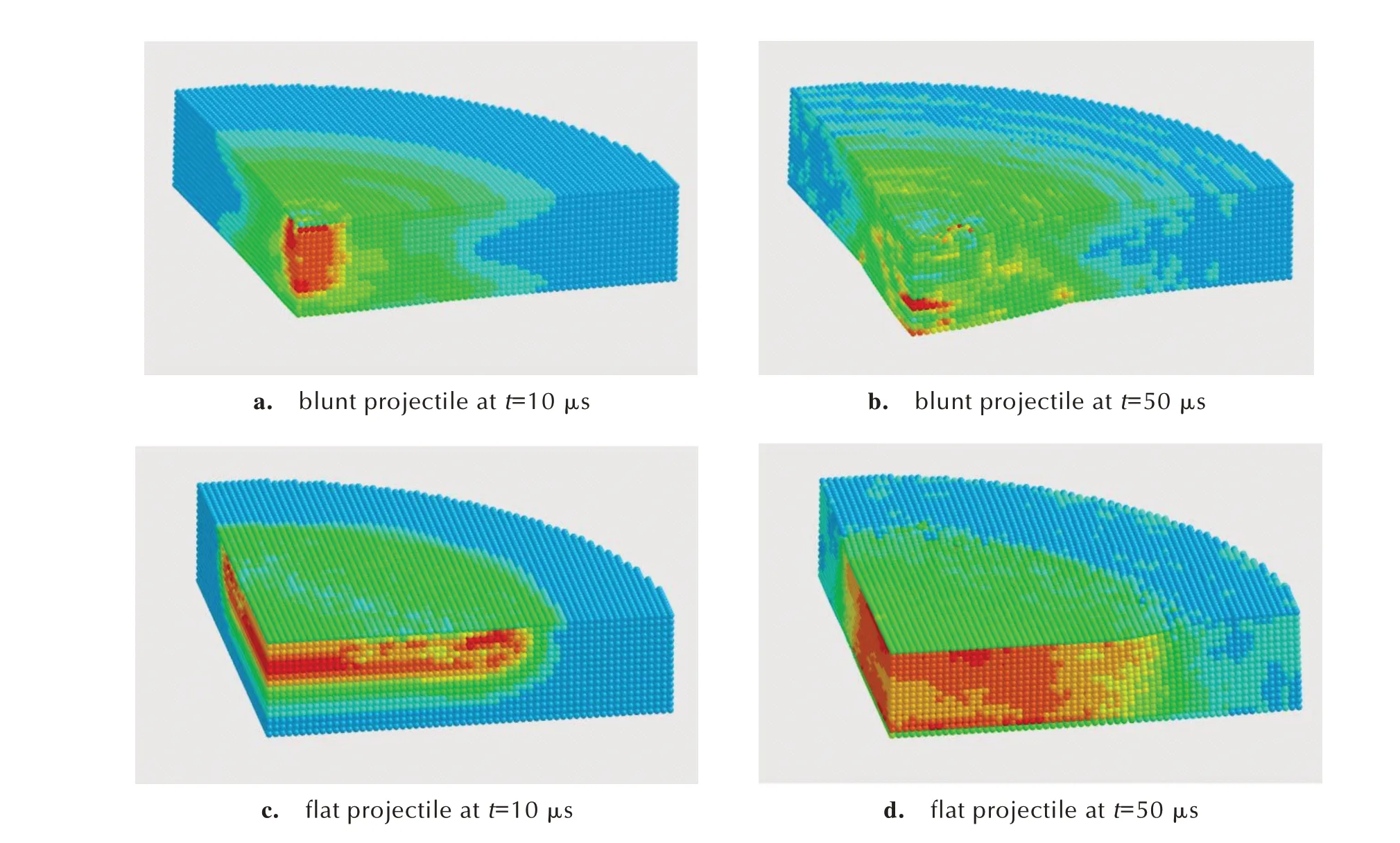
图8 不同形状弹头撞击下PBX-2 炸药的应力分布Fig.8 Stress distribution of PBX-2 under the impact of different projectile heads

图9 为钝头弹与平头弹以不同速度撞击时炸药内部最高温度单元的温度-时间曲线。由图9 可以看出，当钝头弹与平头弹速度低于40 m·s-1时，炸药温度上升比较缓慢，当达到一定温度后便不再升高，未发生点火。当钝头弹与平头弹的速度分别大于45 m·s-1和50 m·s-1时，炸药温度以更快的速率上升，达到点火温度后温度急剧上升发生点火，且点火时间随弹速的增加而减小。分析可知，撞击速度较低时，炸药裂纹出现的时间较晚，摩擦温升比较缓慢；随着撞击速度增加，裂纹间摩擦加剧，自反应放热加快，形成局部热点导致点火。

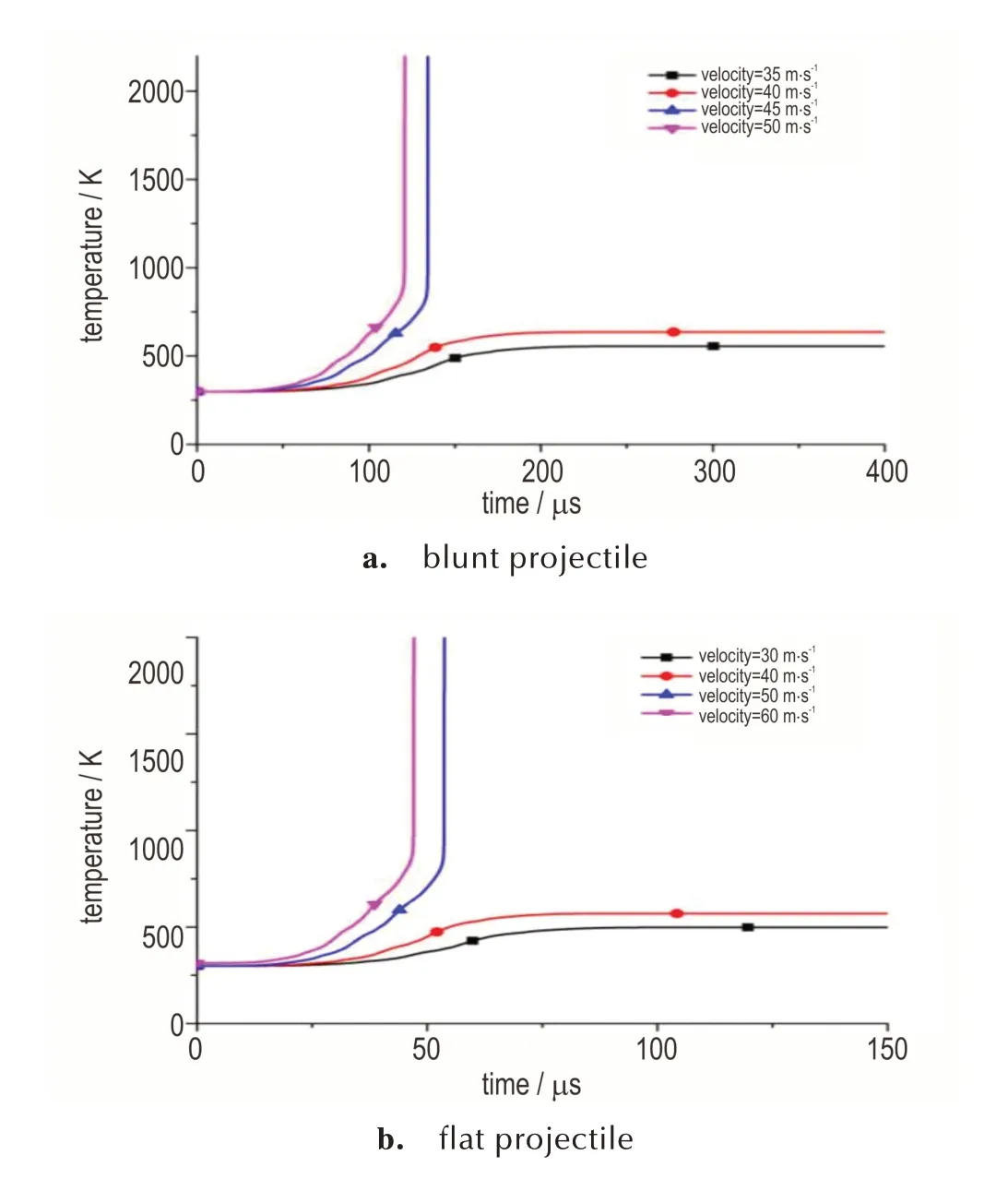
图9 不同速度弹丸撞击下的温升曲线Fig.9 Temperature rise curve under the impact of different projectile velocities

图10 为炸药达到点火临界点时的温度分布。钝头弹加载下，达到点火温度的炸药单元集中于弹头轴线下方附近；平头弹加载下，达到点火温度的炸药单元主要位于弹头圆周下方，呈环状分布。结合图7 中的裂纹分布与图8 中的应力分布可知，钝头弹加载下，轴线下方炸药单元所承受的压力更大，发生断裂后单元间的摩擦作用更强，导致更高的摩擦温升，加速自反应放热，从而更快到达点火温度；平头弹加载下，弹头边缘与盖板接触处发生强烈的剪切作用，发生断裂后此处的炸药单元间相对位移速度更大，导致更高的摩擦温升，加速自反应放热，从而更快到达点火温度。

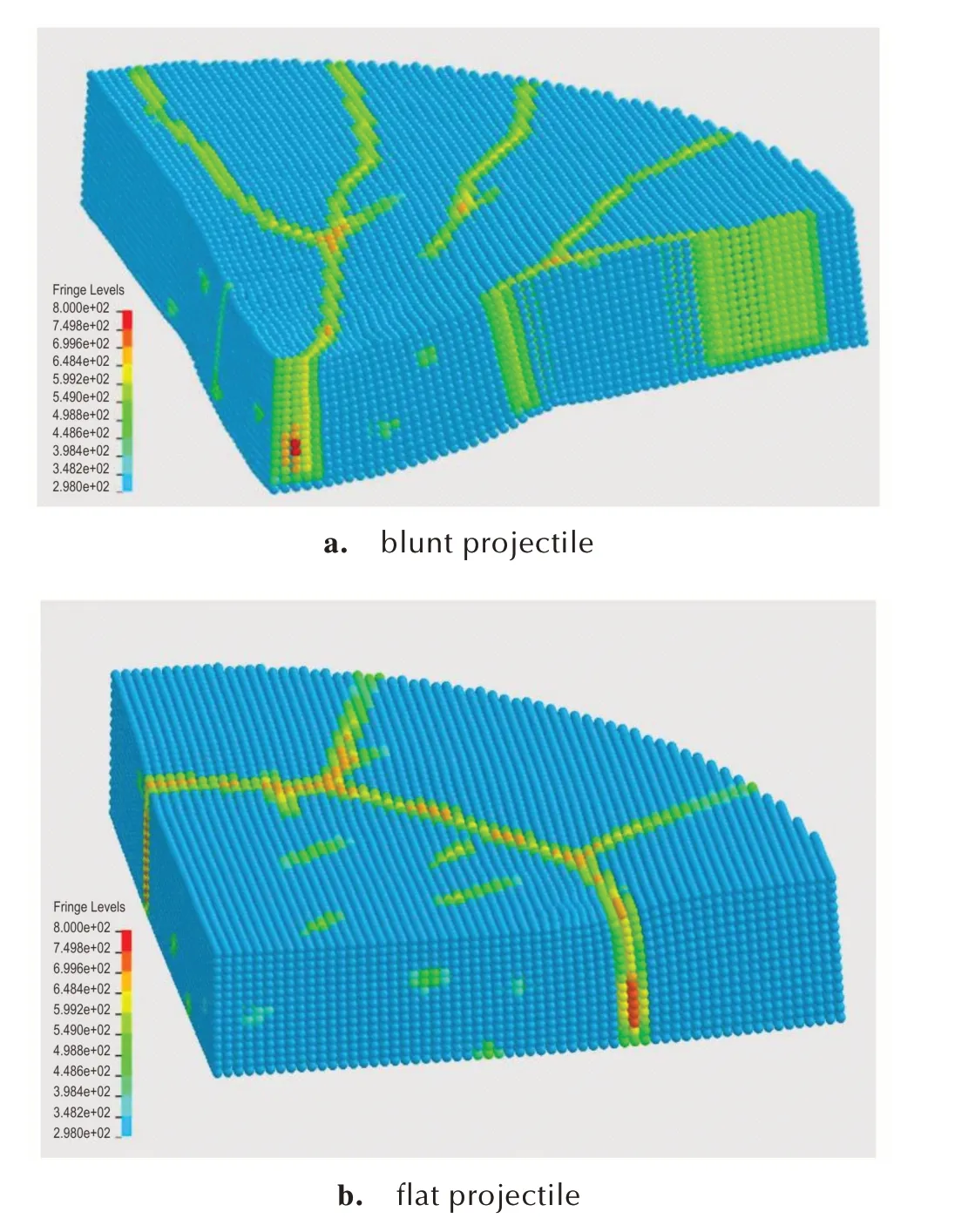
图10 不同形状弹头撞击下炸药的温度分布图Fig.10 Temperature distribution of explosives under the impact of different projectile heads

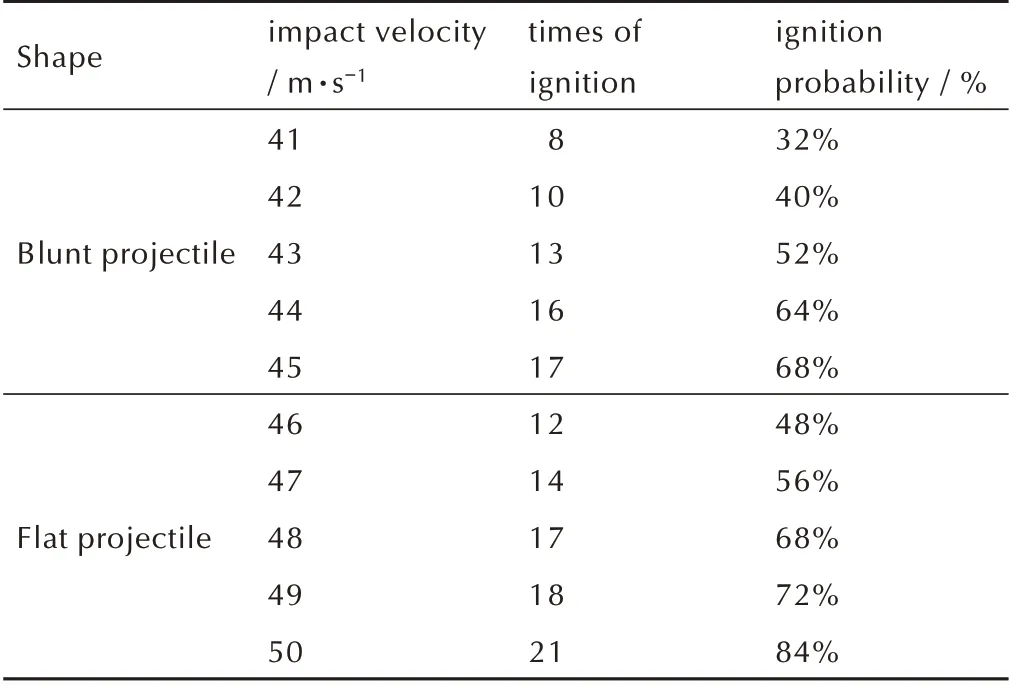
表3 钝头弹不同撞击速度下的点火情况Table 3 Ignition situation of blunt projectile under the impact of different velocities

重复随机生成炸药非均匀模型，对每速度撞击下的点火情况各进行25 次模拟，模拟结果见表3。借鉴落锤实验炸药感度判定标准［16］（一定落高下重复实验点火概率超过50%），可得数值模拟中使炸药点火的速度阈值分别约为43 m·s-1（钝头弹）和47 m·s-1（平头弹），与文献中结果（钝头弹43 m·s-1，平头弹47 m·s-1）对比大致吻合，表明本文中建立的计算模型可以较好地模拟Steven 实验。

图11 为表3 中点火概率100%时的25 次模拟中点火位置的平面分布统计：钝头弹撞击后，点火位置集中分布于距离轴心4～11 mm 处，即点火点围绕撞击轴产生；对于平头弹，点火位置集中分布于距离轴心27～32 mm 处，点火点呈环状分布，与弹头直径大致相当。图11 中的点火位置分布与文献［5］中实验观测到的结果大致相符。

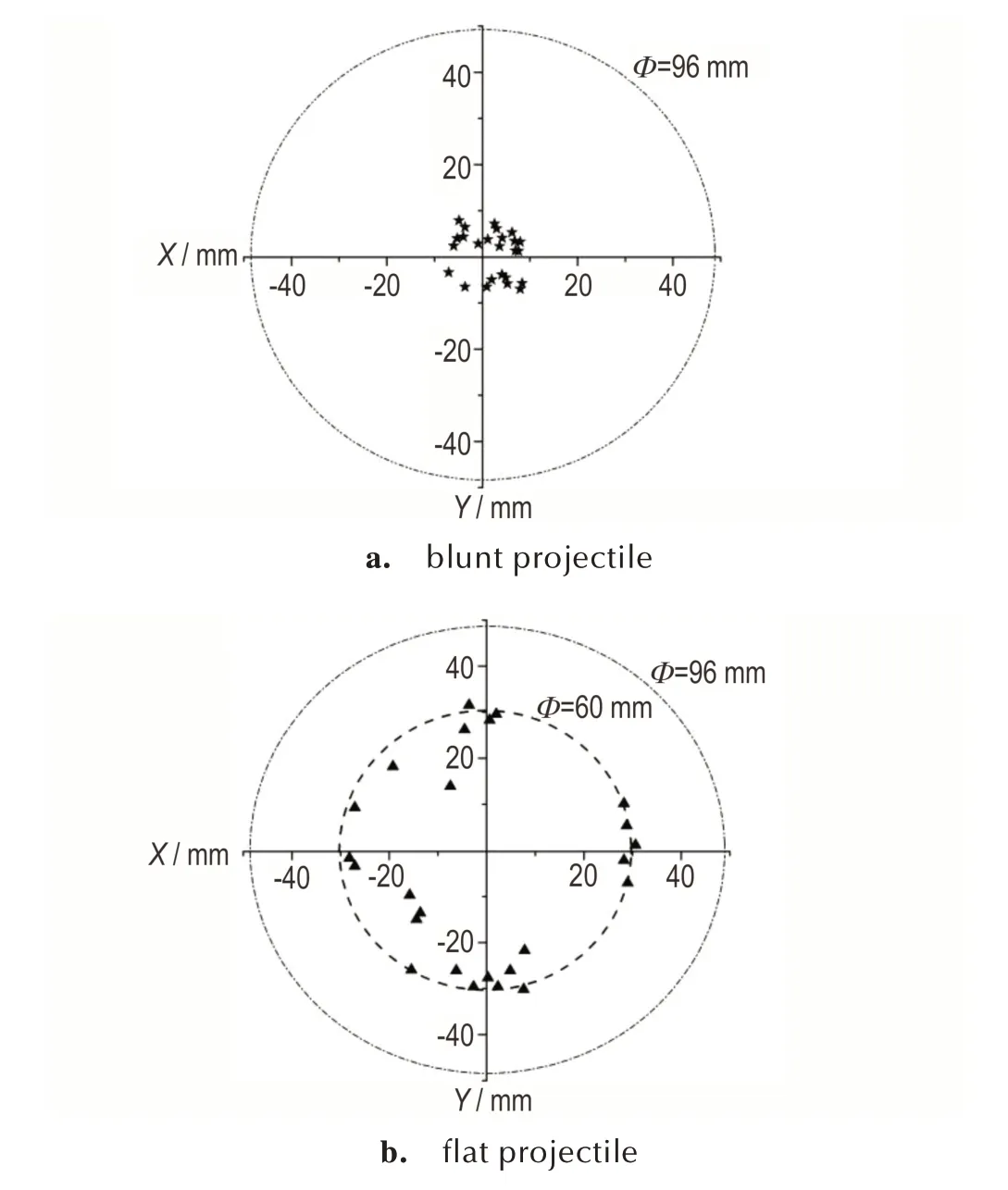
图11 不同形状弹头撞击下炸药点火位置平面分布统计Fig.11 Plane distribution statistics of explosive ignition positions under the impact of different projectile heads

4 结论

本研究采用FEM-DEM 结合方法对Steven 实验中脆性炸药PBX-2 的低速撞击破坏和点火行为进行了研究。

（1）建立了基于FEM-DEM 结合方法的三维非冲击点火计算模型并编写了Fortran 计算程序，通过对PBX-2 炸药的SHPB 实验模拟，验证了程序处理FEM-DEM 界面物理量传递的可靠性，以及所采用的DEM 断裂模型模拟脆性炸药断裂破坏过程的合理性。

（2）考虑了炸药断裂破碎、裂纹摩擦升温与炸药热分解，模拟了Steven 实验中在钝头弹与平头弹加载下PBX-2 炸药的受载应力历史、裂纹分布、温升曲线等结果。钝头弹实验中，裂纹由弹头轴线处沿径向发散，形成多段贯穿裂纹，中心底部形成明显凹陷；在平头弹实验中，裂纹沿弹头圆周附近呈环状分布。

（3）基于考虑了非均质特性的足够数量PBX 炸药样本的模拟，给出了考虑随机分散特性的Steven 实验中的炸药点火阈值速度与点火位置的统计结果。模拟获得的钝头弹与平头弹撞击下引起点火的阈值速度分别为43 m·s-1和47 m·s-1。在钝头弹加载下点火位置集中分布在撞击中轴线附近；在平头弹加载下形成点火环状带，且环状直径与弹头直径相当。本研究从炸药裂纹摩擦以及自反应放热的角度解释脆性炸药的非冲击点火现象，模拟结果与实验报道定性相符。