构建一类非齐次核的Hilbert型积分不等式的等价参数条件

洪 勇， 陈 强

(1. 广东白云学院数学教研室， 广州 510450； 2. 广东第二师范学院计算机科学系， 广州 510303)

设r>0，α，定义函数空间：

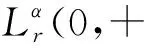
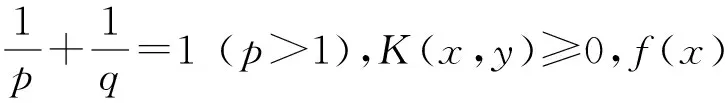
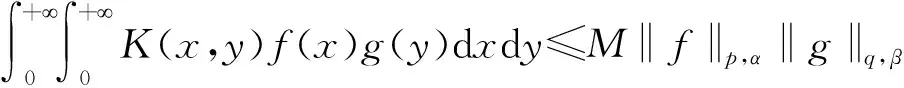
(1)

为以K(x,y)为核的Hilbert型积分不等式.

对于齐次核的情况，选取适当的搭配参数，已获得了许多具有最佳常数因子的Hilbert型不等式[1-10]，研究结果表明：对于不同类型的核，最佳的搭配参数有不同的规律，找出其规律具有重要意义．但在已有研究中，搭配参数的选取大多数是凭研究者的经验得到的[11-15].

1 主要结论及证明

首先给出本文主要定理证明时需用的关于权函数的引理:

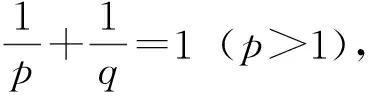
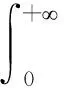
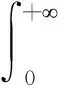
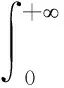
证明先证φ′(t)≥0的情形，此时φ(t)在(0,+)上递增． 作变换t=u，有

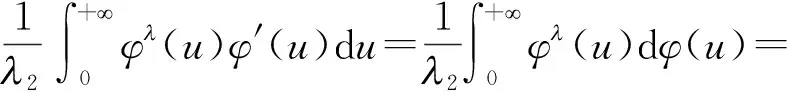
同理可证W2的情形． 作变换xy=t，有

ω1(x)=xφ(t)|φ′(t)|(xt)dt=

xφ(t)φ′(t)tdt=xW1.

同理可证ω2(y)的情形.

类似地可证明φ′(t)≤0的情形． 证毕.

下面给出本文的主要结论.

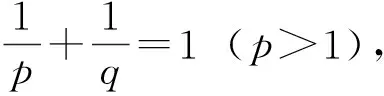
M‖f‖p,α‖g‖q,β,

(2)

其中,f(x)(0,+)，g(y)(0,+).

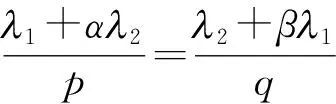
证明记K(x,y)=φ

(i)设式(2)成立． 若c<0，取ε=-c/(212)>0，令

可得

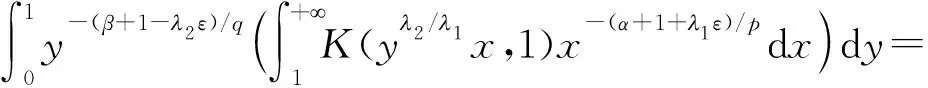
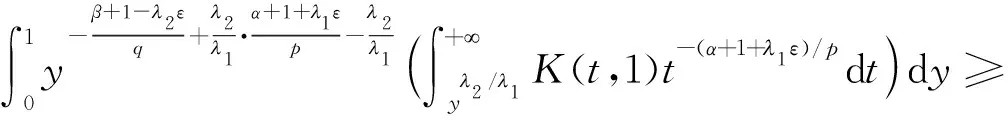
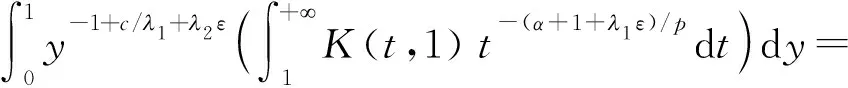
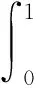
则有

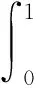
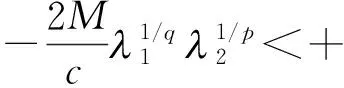
(3)

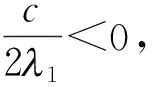
若c>0，取ε=c/(212)>0，令

可得

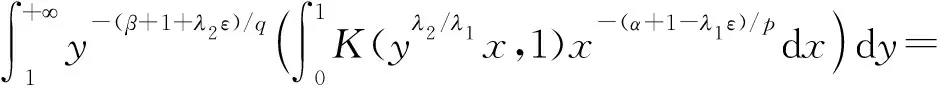
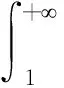
则有

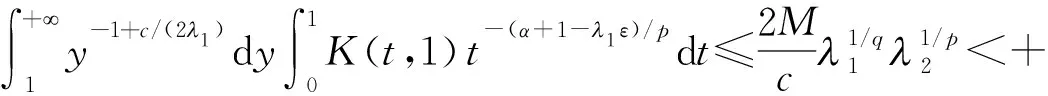
(4)

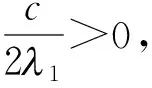
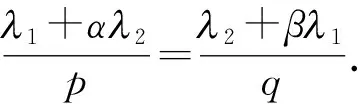
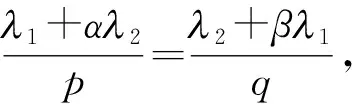
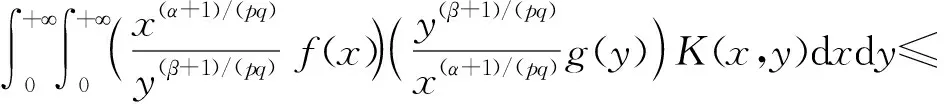
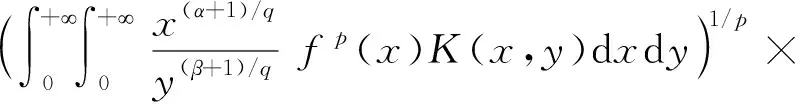
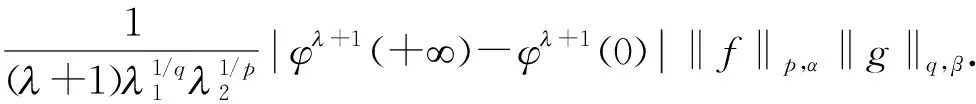
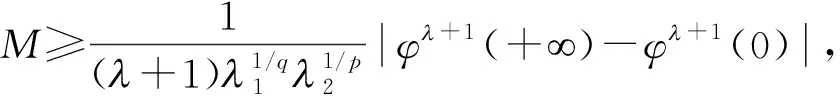
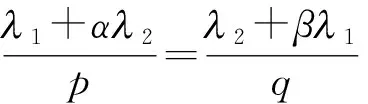
M0‖f‖p,α‖g‖q,β.

取充分小的ε>0及足够大的自然数n，令

可得

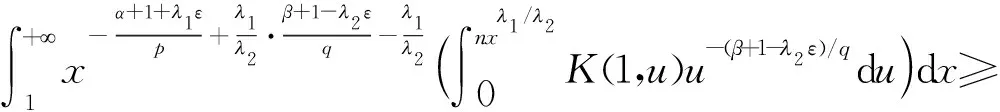
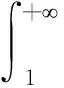
则有

先令ε→0+，再令n→+，得

再由引理1可得

于是可知式(2)的最佳常数因子为:

证毕.

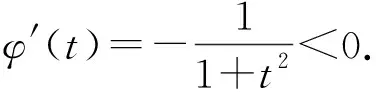
于是可得：

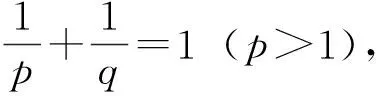
M‖f‖p,α‖g‖q,β,

(5)

其中，f(x)(0,+)，g(y)(0,+).

(ii)当式(5)成立时，其最佳常数因子为：

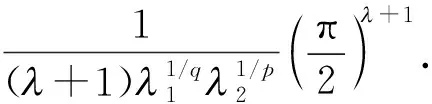
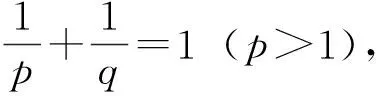
M‖f‖p,α‖g‖q,β,

(6)

其中，f(x)(0,+)，g(y)(0,+).

(ii)当式(6)成立时，其最佳常数因子为：

2 在算子理论中的应用

设K(x,y)≥0,定义奇异积分算子：

则根据Hilbert型不等式的基本理论，式(2)等价于：

‖T1(f)‖p, β(1-p)≤M‖f‖p, α， ‖T2(g)‖q, α(1-q)≤M‖g‖q, β.

则由推论1和推论2，可得

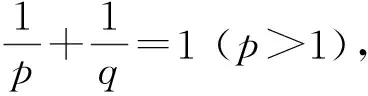
(f(x)(0,+)),

(g(y)(0,+)),

则

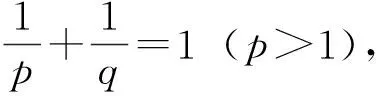
(f(x)(0,+)),

(g(y)(0,+)),

则