具有Beddington-DeAngelis功能反应和分布时滞的病毒动力学模型的稳定性

周欣然, 郑 涛, 张 龙

(新疆大学数学与系统科学学院， 乌鲁木齐 830046)

自20世纪以来，国内外生物动力学的研究进展迅速，许多专家学者都是通过动力学模型来分析病毒感染[1-6],这为更好地理解病毒感染和疾病的控制及不同药物治疗策略效应提供了至关重要的作用.

ANDERSON和MAY[7]介绍了一种具有自由生存阶段的寄生虫模型,NOWAK和BANGHAM[8]将其应用于病毒动力学. 考虑到病毒感染靶细胞过程中普遍存在的非线性感染率,HUANG等[9]提出了一类具有Beddington-DeAngelis功能反应的病毒动力学模型:

(1)

其中，x(t)为健康靶细胞在t时刻的细胞密度，y(t)为感染细胞在t时刻的细胞密度,v(t)为游离病毒在t时刻的细胞密度,为健康靶细胞的生成速率,d为健康靶细胞的自然死亡率,β为病毒感染健康靶细胞的感染率,p为感染细胞的自然死亡率,常数k为每个感染细胞在单位时间内生成的游离病毒数量,u为游离病毒的自然死亡率；并得到了模型(1)的无病平衡点和地方病平衡点的全局渐近稳定性. 又考虑到病毒颗粒接触靶细胞的时间可能与接触细胞受到积极影响的时间存在一定的滞后性,即接触病毒体进入细胞需要时间,HUANG等[10]将细胞内延迟纳入模型,得到了以下离散时滞病毒模型：

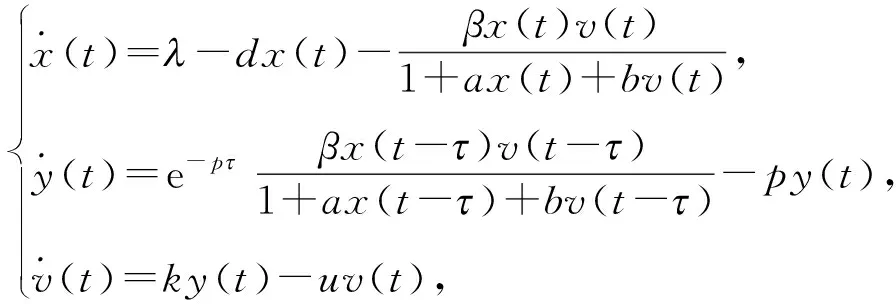
(2)

并通过对特征方程的分析和构造合适的李雅普诺夫函数,建立了模型(2)的无病平衡点和地方病平衡点的局部稳定性；且证明了当R0<1时无病平衡点全局渐近稳定,R0>1时地方病平衡点全局渐近稳定.

基于以上模型，考虑到接触细胞被感染变成感染细胞的滞后时间可能由靶细胞自身细胞内物质决定，即不同靶细胞被感染变成感染细胞的滞后时间是可变的,则可以理想化假设t-到t时刻接触病毒细胞的靶细胞都有可能被感染形成感染细胞，这一现象可以用分布时滞来描述[11]. 又考虑到目前在全世界范围内仍缺乏根治HIV感染的有效药物,现阶段的治疗目标是最大限度和持久地抑制患者体内的病毒复制,而抗逆转录酶药物则是通过抑制病毒感染健康细胞来抑制病毒的复制. 因此，引入参数γ(0,1)来代表药物对病毒感染的抑制作用. 为了更加细致地描述病毒感染健康靶细胞后的滞后效应以及了解药物治疗参数γ对艾滋病治疗的影响，本文建立了如下数学模型：

(3)

其中,x(t)为健康靶细胞在t时刻的细胞密度,y(t)为感染细胞在t时刻的细胞密度,v(t)为游离病毒在t时刻的细胞密度,s为健康靶细胞的生成速率,d为健康靶细胞的自然死亡率,β为描述细胞感染的速率,γ(0,1)为抗逆转录酶对病毒感染健康靶细胞的抑制率,为在t-到t时刻接触病毒的健康靶细胞被感染变成感染细胞的个数,p为感染细胞的自然死亡率,常数k为每个感染细胞在单位时间内生成的游离病毒数量,u为游离病毒的自然死亡率.

本文主要讨论了模型(3)解的正性和有界性, 得到了该模型的基本再生数R0;讨论了该模型的无病平衡点局部渐近稳定性和全局渐近稳定性的判定准则(R0≤1,R0<1);最后,通过数值模拟验证本文结论的有效性.

1 解的非负性与有界性

设C=C([-,0];3)是[-,0]到3上的连续函数全体所形成的具有上确界范数的Banach空间,模型(3)的初始条件为：

x(θ)=φ1(θ)，y(θ)=φ2(θ)，v(θ)=φ3(θ)，θ[-,0]，φi(θ)≥0，φi(0)>0 (i=1,2,3)，

(4)

其中，φ=(φ1,φ2,φ3)TC.

由文献[12]知:模型(3)满足初始条件(4)的任意解(x(t),y(t),v(t))T在[-,)上存在且唯一. 在此条件下，可得:

定理1设(x(t),y(t),v(t))T为模型(3)在初始条件(4)下的任意解,则任意解(x(t),y(t),v(t))T非负且最终有界.

证明首先证明模型(3)在初始条件(4)下的任意解都为正. 先证x(t)≥0. (反证)假设对任意的t≥0,存在t1>0,x(t1)=0且x(t)>0. 当t[0,t1)时,有

因此,

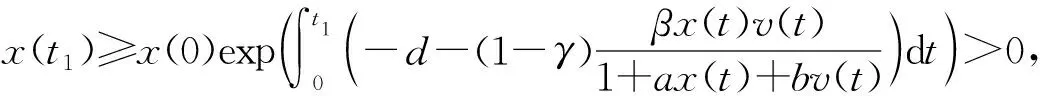
这与假设x(t1)=0矛盾.

同理,假设对任意的t≥0,存在t1>0,y(t1)=0且y(t)>0. 当t[0,t1)时,有

(5)

由式(5)，有

这与假设y(t1)=0矛盾.

同理,由于y(t)>0,则有

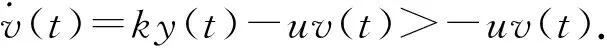
(6)

对式(6)两边同时积分,可得

(7)

这与假设v(t1)=0矛盾，因此，模型(3)的任意解(x(t),y(t),v(t))T的非负性得证.

接下来,证明任意解(x(t),y(t),v(t))T最终有界. 对于模型(3)的第1个等式,有

(8)

由比较定理[12]可知,

(9)

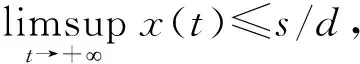
定义

(10)

且δ=min{d-1,p}. 对式(10)两边同时求导,有

s-δF(t).

(11)

由比较定理可知F(t)有界，从而y(t)有界；再由模型(3)的第3个等式可知v(t)有界. 故模型(3)的任意解(x(t),y(t),v(t))T最终有界.

2 平衡点及无病平衡点的局部渐近稳定性

模型(3)总存在一个无病平衡点E0(x0,0,0)，其中x0=s/d. 下面将分析模型(3)是否存在正的地方病平衡点.

若模型(3)存在正的地方病平衡点，则平衡点需满足以下等式：

(12)

由式(12)可得

若要满足地方病平衡点的正性，则要求x*>0，即(1-e-d)[kbd+(1-γ)βk]-adpu>0，即要满足

(13)

由于

(14)

则可定义模型(3)的基本再生数为：

因此，以R0为阈值可得以下结论：

定理2若R0<1，则模型(3)的无病平衡点E0局部渐近稳定；反之，E0不稳定.

证明系统(3)在E0处的特征方程为

(1-γ)e]=0，

(15)

f()=(+p)(

(16)

下面分2种情况讨论.

(17)

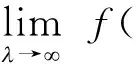
f()=(+p)(

(18)

等价于

G(

(19)

矛盾，所以x<0，即此时f()的根具有负实部. 因此，当R0<1时,E0是局部渐近稳定的.

3 无病平衡点E0的全局渐近稳定性

定理3对于模型(3),若R0≤1,则无病平衡点E0全局渐近稳定.

证明设x0=s/d，则模型(3)等价于：

(20)

定义李雅普诺夫函数

(21)

其中

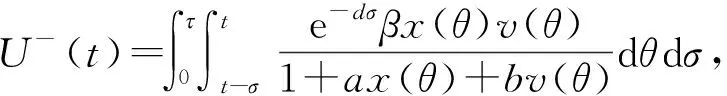
则有

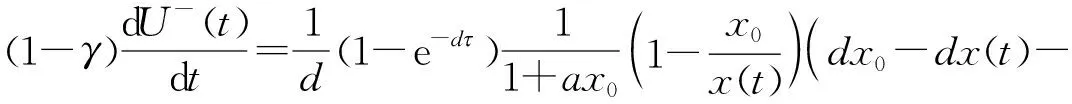
(22)

由式(22)可知:当R≤1时,dV/dt≤0；当dV/dt=0时，v=0当且仅当x=x0. 由拉萨尔不变原理可知E0是全局渐近稳定的.

4 数值模拟

本节通过MATLAB软件进行数值模拟,以验证该模型的无病平衡点具有全局渐近稳定性. 在此取定相应系数值与初值：a=0.6,b=0.8,d=0.1,s=0.8,β=0.4,p=0.5,k=0.3,u=0.2,γ=0.5.(x(0),y(0),v(0))分别取为(9.5,5.5,6.6)、(7.4,4.8,5.3)、(6.8,5,6)、(4.4,3.1,4.8)、(5,3.2,4)、(14.5,3.2,2.6)、(2,3.2,2.6).

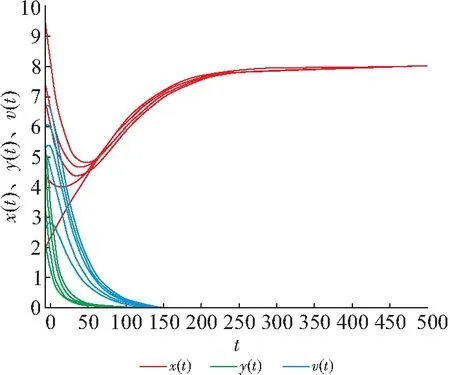
图1 模型(3)的时间序列图(R0<1)Figure 1 The time series plot of model(3) when R0<1

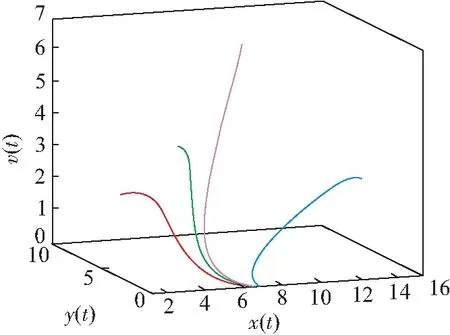
图2 模型(3)的三维空间相图(R0<1)Figure 2 The 3-dimensional phase diagram of model (3) when R0<1注：颜色不同的曲线代表初值不同的解曲线.

由图1可知：x(t)随着时间的增加达到一定值,y(t)、v(t)随时间的增加而最终趋于0. 由图1和图2可知：对任意给定的初值,x(t)、y(t)、v(t)最终趋于x轴的一定值E0=(8,0,0). 由此可知：无病平衡点在R0<1时全局渐近稳定.

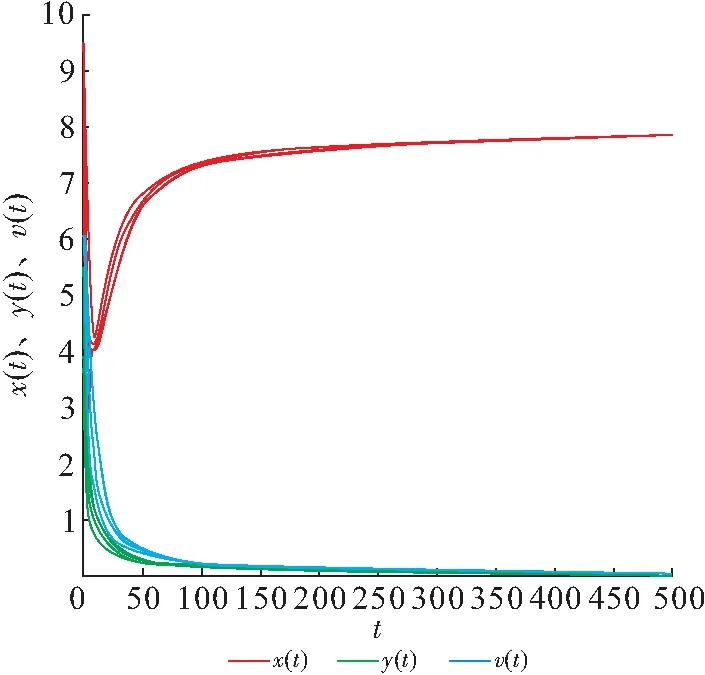
图3 模型(3)的时间序列图(R0=1)Figure 3 The time series plot of model(3) when R0=1

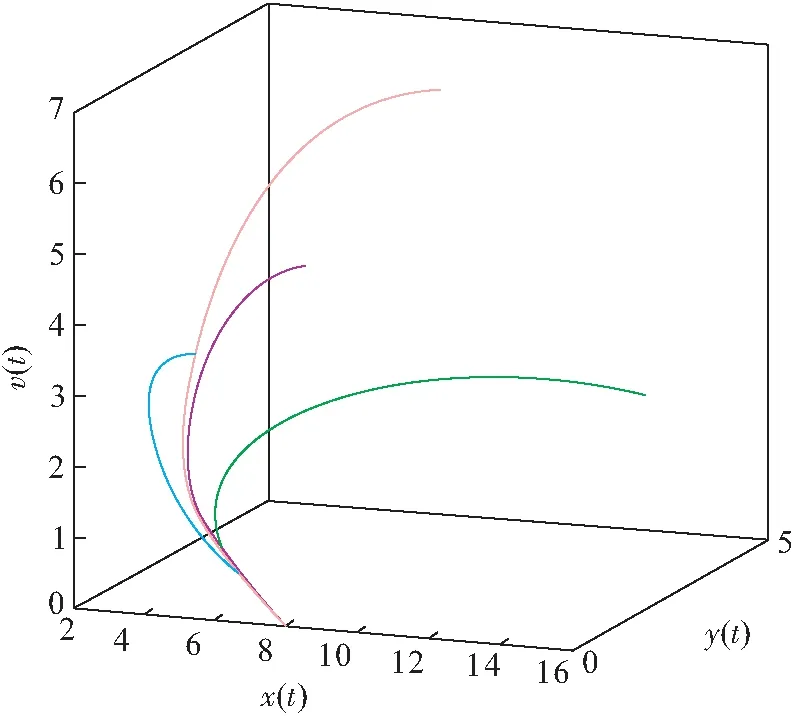
图4 模型(3)的三维空间相图(R0=1)Figure 4 The 3-dimensional phase diagram of model(3) when R0=1注：颜色不同的曲线代表初值不同的解曲线.

由图5可知：x(t)随着时间的变化达到一定值, 但y(t)、v(t)并未随时间的变化而消亡, 故此时无病平衡点不稳定. 由图5和图6可知：对任意给定的初值,x(t)、y(t)、v(t)最终趋于一定值E*=(2.971 4,4.859 1,7.288 7). 由此可知：地方病平衡点在R0>1是全局渐近稳定.

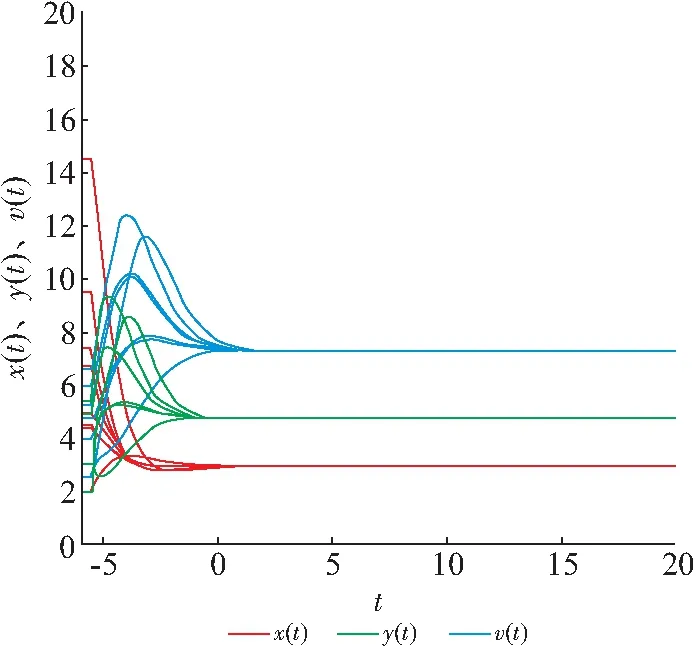
图5 模型(3)的时间序列图(R0>1)Figure 5 The time series plot of model(3) when R0>1

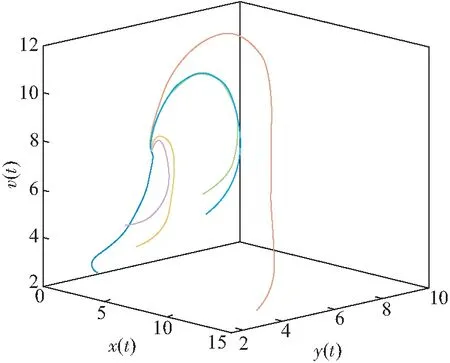
图6 模型(3)的三维空间相图(R0>1)Figure 6 The 3-dimensional phase diagram of model(3) when R0>1注：颜色不同的曲线代表初值不同的解曲线.

5 小结

本文建立了具有Beddington-DeAngelis功能反应和分布延迟的病毒动力学模型，并讨论了该模型的稳定性. 为了研究药物对病毒感染的抑制作用，引入了药物治疗参数γ(0,1),并求解该模型在药物治疗下的基本再生数R0,通过分析该模型的特征方程,证明了该模型的无病平衡点E0的局部渐近稳定性;通过构造合适的李雅普诺夫泛函和利用李亚普诺夫-拉萨尔型定理,证明了该模型的无感染平衡点E0在R0≤1时的全局渐近稳定性;通过Matlab验证了本文结论的有效性. 本文虽然没有讨论地方病平衡点的全局渐近稳定性,但由数值模拟可知地方病平衡点E*的全局渐近稳定性,由三维空间相图可知地方病平衡点E*在R0>1时是全局渐近稳定的.