精密仪器厂房微振动实测与数值模拟分析*

高广运 钟 雯 孟 园 耿建龙

(①同济大学地下建筑与工程系，上海 200092，中国)(②同济大学岩土及地下工程教育部重点实验室，上海 200092，中国)

0 引 言

现代科技发展使得机械制造业，如光学工业、半导体工业、微电子工业等进入精密甚至超精密时代。随着精密设备的各项技术日趋成熟，精密设备的加工精度逐步达到纳米级水平，振动成为影响精密设备加工精度的一个重要因素。在精密设备生产时，厂房的微振动会导致机床整体发生振动，甚至使刀具和加工材料间出现不同程度的位移，最终导致产品精度和表面质量出现问题。因此，精密仪器厂房微振动特性分析和评价非常重要。

目前，对精密仪器厂房微振动的分析和评价主要从厂房或设备隔振研究和厂房结构振动特性研究两方面展开。在厂房结构振动特性研究方面，研究工作主要集中于振动实测以及厂房结构的数值模拟分析。在振动实测方面，高广运等(2018)对某电子工业厂房进行24 h现场实测，分析了场地的振动特性和路面交通荷载引起的环境振动随距离衰减特性；李锡伟(2018)对某微电子芯片厂房进行现场实测，分析了复杂环境下场地微振动情况，并相应提出了场地规划和隔振建议；高广运等(2020)对某主体结构完工后的电子工业厂房进行实测，对自由场地和厂房主体结构的微振动响应进行对比，提出了厂房防微振设计建议。在数值模拟方面，胡晓勇等(2006)建立了某洁净室有限元模型，分析了该结构的振动特性和对环境微振动的响应，并评价了其结构防微振性能；雷自学等(2013)建立了轻骨料混凝土厂房的有限元模型，对比普通混凝土厂房模型分析了不同阻尼比下的动力响应；Gao et al.(2017)建立了某高科技电子厂房的有限元模型，发现桩筏基础能够降低厂房的微振等级；李泽熙等(2019)分别采用实体单元和杆单元，分析了单元类型对微振结构有限元计算的影响，发现使用实体单元进行微振分析时结果更加准确。综上所述，目前国内外对精密仪器厂房结构振动特性研究仍然较少，需要通过现场实测和数值模拟对厂房微振动特性作进一步的分析。

本文结合苏州工业园区某高科技电子工业厂区一单层轻钢结构厂房微振动测试分析项目，在厂房建成前后对地坪振动进行了现场实测和评价，并建立其有限元模型分析了Rayleigh阻尼和底板厚度对厂房防微振地坪振动的影响，研究结果可为类似的精密仪器厂房设计提供参考。

1 工程概况

该高科技电子工业厂区位于苏州工业园区出口加工区内，苏虹东路北侧，总占地面积约8860 m2，厂区总平面图如图1所示。厂区拟建精密仪器厂房为单层轻钢结构，带有局部二层更衣室。厂区周围环境振动复杂，其中场地西侧约20 m处为已建厂房，南侧约50 m处为已建厂房，北侧为一块宽约150 m的未开发土地，周围有分散的施工车辆，场地北侧约300 m米处为一条东西方向的道路，交通繁忙。

图1 厂区总平面图

厂房采用桩筏基础，筏板尺寸为132.5 m×65.3 m，厚度为0.5 m，精密仪器设备安装在地板上。基础采用PHC 400 AB 95,15预应力高强混凝土管桩，桩径400 mm，壁厚95 mm，桩长15 m，桩尖的承载层位于第5层土壤(粉砂)中，桩位布置情况如图2所示。

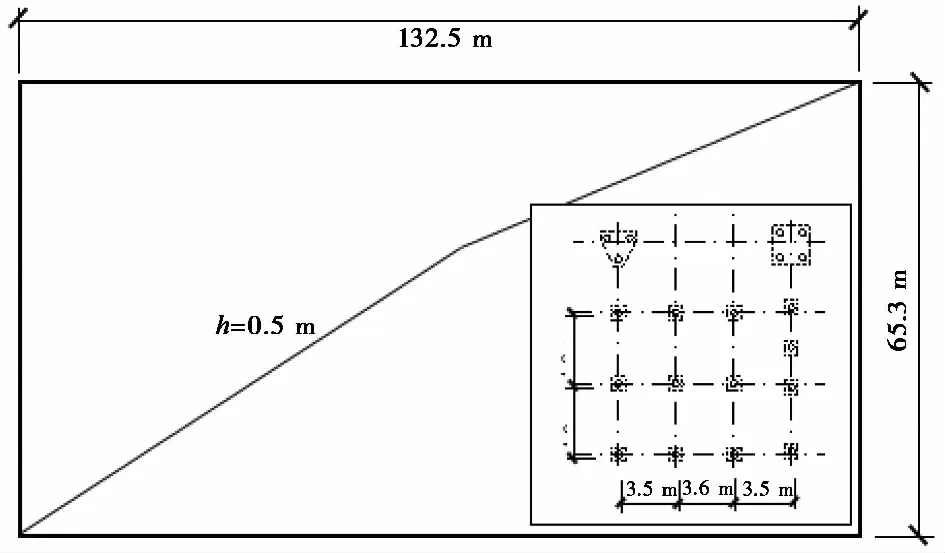
图2 成品仓库区桩位布置图

本场地地貌单元属于长江三角洲河口冲湖积平原，在勘察揭露的35.45 m深度范围内，自上而下分为9层土，各土层性质如表1所示，测量的稳定水位距地面0.9～1.2 m。

表1 土层分布及主要物理力学性质指标

2 厂房振动实测分析

为分析该精密仪器厂房在厂房机械振动、周围道路车辆行驶等作用下的微振动特性，选取厂房地坪表面中柱柱底处一点为研究对象，在厂房建成前后分别测试了该点的地面振动。由于精密仪器振动需满足国际振动标准ISO2631中的VC-B标准(Class B of Generic Vibration Criteria)，因此还将测试结果分别与测试标准进行了对比，测点位置如图3所示。

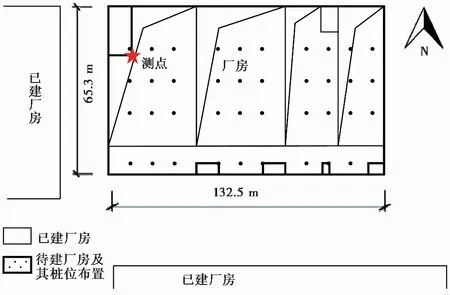
图3 测点布置情况图

选取厂房建成前后测点19.5 s的加速度实测数据绘制1/3倍频程图如图4所示，并在图中绘制VC-B测试标准进行比较。

由图4a可知，厂房建成前，场地东西方向振动加速度均方根值位于5×10-4～3×10-2gal范围内，南北方向位于1×10-3～2×10-1gal范围内，竖直方向位于1×10-3～4×10-2gal范围内。除了8 Hz附近频段外，东西方向振动速度均方根值均略大于南北和竖直方向，且满足VC-B微振动控制标准。在8 Hz附近，测点水平方向振动速度和加速度值均较大，且南北方向振动略超出VC-B标准。

图4 厂房建成前后测点1/3倍频程图

由图4b可知，厂房建成后，场地东西方向振动加速度有效值位于2×10-4～2×10-2gal范围内，南北方向位于6×10-4～2×10-2gal范围内，竖直方向位于3×10-4～3×10-2gal范围内，较厂房建成前均有不同程度的减小，说明厂房的桩筏基础有明显的减振效果。测点3个方向振动大小均位于VC-B曲线下方，满足振动控制要求。整体而言，厂房建成后竖直方向振动速度均方根值大于水平方向，这与厂房建成前的测试结果有所差异。

对比两图曲线可知：厂房建成后，在水平方向上，60 Hz以下的频段范围内振动有所减小，而在60～100 Hz高频段内振动值反而增大；在竖直方向上，厂房地坪振动值变化呈波动趋势，1～2 Hz、6～8 Hz和10～20 Hz频段内振动有所减小，而在2～6 Hz、30～100 Hz频段内增大，说明厂房的存在对不同方向、频段地面的振动影响有所差异。

3 精密仪器厂房有限元模型的建立

为了进一步分析厂房的设计参数对厂房振动特性的影响，本文基于ANSYS建立了相应的有限元计算模型进行分析。由于厂房结构振动幅值很小，应变小于1.0×10-5，属于弹性变形，因此本文选用线弹性本构计算模型。基于以上分析，柱、主次梁采用Beam188单元，混凝土底板采用Solid65单元，材料计算参数、构件尺寸如表2和表3所示。参照厂房设计图纸，建立的厂房有限元模型如图5所示，图中测点位置处即前文中的现场实测所处的位置。

表2 模型材料参数

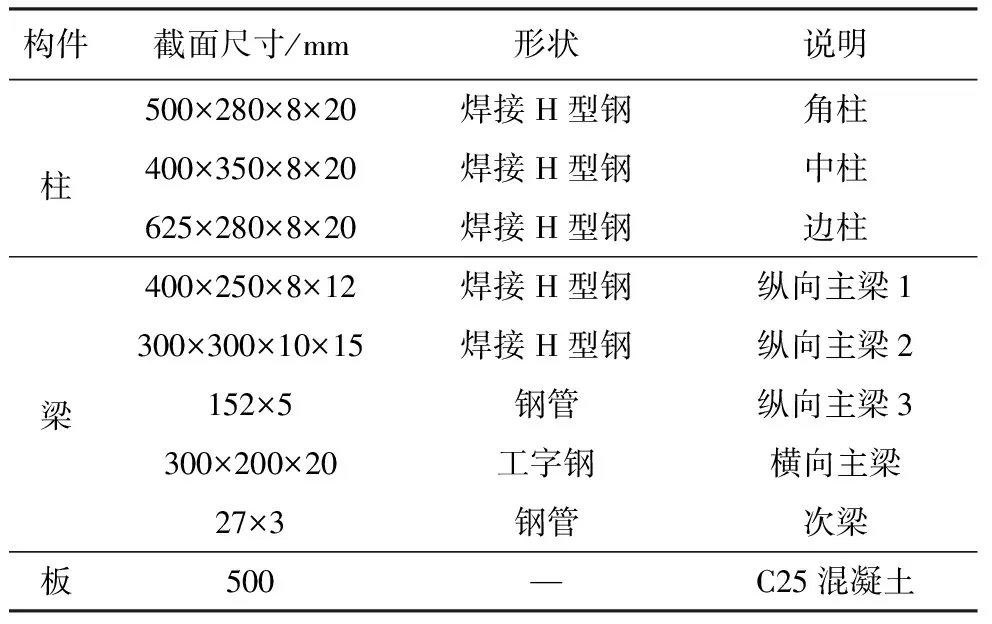
表3 模型构件尺寸取值表

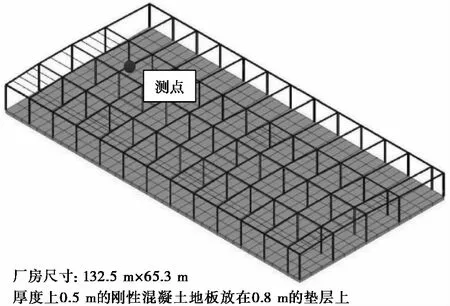
图5 厂房有限元模型

截取场地环境实测数据中加速度幅值最大的19.5 s数据(图6)作为输入激励荷载施加在模型底部。输入加速度激励时，先约束住模型底板底部所有节点3个方向上的自由度，之后在整个模型的每个节点上施加3个方向的加速度激励。模型计算时间取19.5 s，设置4999个荷载步，每个荷载步包括3个荷载子步。为考虑结构固有阻尼对计算结果的影响，模型采用Rayleigh阻尼，并设置阻尼比为5%。

图6 输入的加速度时程数据曲线

4 模型可靠性验证

为验证所建立有限元模型的可靠性，将厂房正常运行条件(包括工作人员行走、周边车辆行驶及其他生产设施运行)下的测点振动实测值与该点数值计算结果进行对比，3个方向上的1/3倍频程对比结果如图7所示。

图7 测点实测结果和数值模拟结果的1/3倍频程对比图

由图7可知，在东西方向上，计算值和实测值的振动幅值接近，均处于8×10-5～2×10-2gal范围内。在7 Hz以下频段内，测点计算值小于实测值，而7 Hz以上频段内，较实测值偏大。在南北方向上，两者的振动幅值也相近，均处于1×10-4～2×10-2gal范围内，在7 Hz以下频段内，测点计算值小于实测值，相差约6倍，在7 Hz以上频段内，两者变化趋势相似，振动幅值相差较小。在竖直方向上，计算值整体上较实测值小，尤其在10 Hz以下频段内相差较多，而在10～50 Hz频段内两者振动幅值相差较小，之后振动幅值均减小。

整体而言，测点计算值在各个频段内的变化趋势和场地环境振动的较一致，能够反映厂房的振动特性。在7 Hz以上频段，有限元模拟效果较好；但对于7 Hz以下频段，3个方向的计算值均小于实测值，这可能是由于模型对该厂房的桩筏基础和路基土简化造成的。

5 精密仪器厂房设计参数分析

改变主体结构和地基基础的主要计算参数，如阻尼比、底板的厚度等，可以改变厂房的质量、刚度、自振周期，进而影响地坪的振动情况。本节分析了厂房结构设计参数对厂房微振动特性的影响。

5.1 阻尼的影响

阻尼是结构体系在振动过程中能量耗散的各种因素的总称，它反映了结构体系振动过程中能量的耗散特征。阻尼越大，系统的能量消耗越快，系统从受激发状态恢复到先前状态所花费的时间越短，即系统越稳定。由于阻尼是能量的转换或消散，因此阻尼技术是控制结构振动的有效方法。考虑到Rayleigh阻尼应用广泛、物理意义明确、使用便捷，本文采用Rayleigh阻尼作为阻尼输入方式，并选取Rayleigh阻尼的振型阻尼比为3.5%、5.0%、6.0%进行分析。不同Rayleigh阻尼下，测点的1/3倍频程对比结果如图8所示，并汇总得到加速度最大值和主导频率如表4所示。

表4 不同Rayleigh阻尼下测点加速度最大值和主频

图8 不同Rayleigh阻尼下测点1/3倍频程对比图

由图8可知，在3个方向上，测点振动速度均随着Rayleigh阻尼比的增大而减小，在1～3 Hz、10～50 Hz频段内减小显著，而在其他频段减小不明显。在1～3 Hz附近，振动加速度随阻尼比增加而减小，且减小幅度较大；在3～10 Hz附近，不同阻尼比下振动加速度值相近，振动幅值均呈上升趋势，且在南北方向和垂直方向出现峰值振动；在10～50 Hz附近，振动加速度值差异较大，且振动加速度随阻尼比的增大而减小，东西方向在该频段内出现峰值振动；在50～100 Hz附近，振动加速度值开始衰减，不同阻尼比下的振动加速度值差异逐渐减小。

由表5可知，在不同的Rayleigh阻尼比下，3个方向上加速度最大值各不相同，这可能是由阻尼比的各向异性导致的。随着Rayleigh阻尼比的增大，各个方向上的振动加速度最大值均逐渐减小，最大减幅为32.74%。当结构的Rayleigh阻尼改变时，主导频率在东西方向和南北方向几乎没有变化；在竖直方向，主导频率随阻尼比的增加而降低，并趋于稳定。因此，在厂房防微振设计时，适当增加阻尼不会改变厂房振动主频，但可显著减小中低频振动，达到较好的减振效果。

表5 不同底板厚度下的加速度峰值和主频

5.2 底板厚度的影响

选取底板厚度为0.4 m、0.5 m和0.8 m，分析了底板厚度对高科技厂房微振动特性的影响。不同底板厚度下测点的1/3倍频程计算结果对比情况如图9所示，并汇总得到不同底板厚度下的加速度最大值和主导频率如表5所示。

图9 不同底板厚度下测点1/3倍频程对比图

由图9可知，测点振动速度随着底板厚度的增大而减小，底板厚度为0.8 m时的振动速度较底板厚度为0.4 m和0.5 m时减小幅度较大。在50 Hz以下频段内，3个方向的速度均方根值均随底板厚度的增大而减小，其中竖直方向上的1～3 Hz频段和10～50 Hz频段内减小尤为显著；在50 Hz以上频段内，水平方向的振动速度随底板厚度的增加变化较小，但竖直方向振动速度差异仍比较明显。

由表5可知，测点加速度峰值随底板厚度的增大而减小，其中东西方向加速度峰值减少幅度最大，最大减幅为35%。而底板厚度改变时，测点主导频率几乎不产生变化。因此，在厂房防微振设计时，可以通过适当增加底板厚度来减小中低频振动，从而使厂房振动达到设计要求。

6 结 论

本文基于苏州某高科技电子工业厂区一单层轻钢高科技电子厂房工程，对比了厂房建成前后地面振动大小，利用ANSYS软件分析了设计参数对厂房振动特性的影响，并对该厂房防微振设计提出了建设性意见，主要结论如下：

(1)厂房建成前，地坪振动在部分频段超过了VC-B标准，而在厂房建成后所有频段均满足该标准。

(2)厂房建成后的地面振动实测值较建成前均有不同程度的减小，说明厂房的桩筏基础有明显的减振效果。而在不同方向和不同频段上，振动加速度的变化规律又有所不同，说明厂房的存在对不同方向、频段地面的振动影响有所差异。

(3)有限元计算值的变化趋势与地面振动实测值较为一致。7 Hz以上频段，有限元模拟效果较好；但对于7 Hz以下频段，3个方向的计算值均小于实测值。

(4)阻尼比对结构主频影响较小，而对振幅影响较大。厂房3个方向上的振幅均随着Rayleigh阻尼比增大而减小，在1～3 Hz、10～50 Hz的频段内变化尤为显著，而在其他频段变化不明显。

(5)底板厚度的变化对结构主频影响较小，而对厂房振动大小影响较大。在50 Hz以下，底板厚度变化对振动影响较大，而在50 Hz以上影响较小。因此，在厂房防微振设计时，适当增加底板厚度和阻尼可显著减小中低频振动，达到较好的减振效果。