封闭系统单向冻结淤泥质黏土水分迁移特性研究*

唐益群 赵文强 周 洁

(同济大学土木工程学院，上海 200092，中国)

0 引 言

冻胀现象是工程建设中不容忽视的一个重要问题。无论是寒冷地区季节性冻土的反复冻胀，或是温暖地区人工地层冻结法施工引起的地层冻胀，都给地表建构筑物运营及地下空间开发带来极大的危害(丑亚玲等，2018；胡渊等，2018；杨忠平等，2019；赵建军等，2019)。尤其当在交通工程中采用冻结法施工时，冻胀会引起隧道轴线变形或机场跑道开裂，轻则造成建构筑物使用寿命减损，重则引发严重安全事故(Zhou et al.，2015；Tang et al.，2019)。

为揭示引起冻胀的原因及其影响因素，国内外学者进行了大量的研究工作。早在20世纪20年代，研究人员在封闭系统中进行了一些冻胀试验，并将冻胀现象简单地归因为土中水分在冻结温度下发生相变引起的体积膨胀。然而这种观点无法对冻土中规律分布的冰晶体分凝层的出现作出合理的解释。直到20世纪30年代，Taber(1930)在开放系统冻胀试验中使用相变后体积缩小的液态苯和硝基苯代替水，仍然观察到土体冻胀现象，这种错误的观点才得到纠正。研究人员开始认识到在土的冻结过程中除了原位孔隙水的相变之外，还存在着水分迁移过程(Taber，1929，1930；Biermans et al.，1978)。Ferguson et al.(1964)和Hoekstra(1966)均发现在温度梯度的作用下，土在冻结过程中存在水分从未冻区向冻结区迁移的现象，随后大量的水分迁移试验证实了水分迁移是导致土体冻胀的最主要原因(Perfect et al.，1980；Prat，1986；Konrad，1989；Nassar et al.，1997；Xu et al.，1997；Hermansson et al.，2005；高玉佳等，2010；张辉等，2015)，且温度梯度和冻结速率是开放系统中影响水分迁移通量的关键因素。

依据丰硕的水分迁移试验观测，研究人员提出了多种水分迁移理论以对冻结过程中水分迁移的驱动力进行解释。Beskow(1935)通过研究发现，土在冻结过程中的未冻水含量与土在干燥过程中的残余含水量相似。据此，Penner(1959)、Everett(1961)认为冻结过程中土中水的迁移类似于水在干燥多孔介质中的毛细上升现象，是由冰-孔隙水交界面的表面张力所驱动。然而毛细理论低估了冻胀过程中产生的冻胀压力，并且无法解释冻土中冰晶体分凝层位置滞后于冻结锋面位置的现象，因此毛细理论未能获得更进一步的发展和应用。而薄膜理论则起源于对土中未冻水膜的研究。Bouyoucos(1920)意识到在冻结过程中当温度低于土中水的冻结温度时，土中仍会有一定量的未冻水存在。在冰-土颗粒交界面，由于不同相态的不同材料之间存在分子间作用力，这种作用力使得冰晶体在冰-土颗粒交界面发生融化形成数纳米厚度的未冻水膜，其厚度是温度的函数(Dash，1989)，在暖面较厚而在冷面较薄。由于未冻水膜厚度极小，早期研究人员难以对其性质进行有效研究，因此仅笼统地认为未冻水膜与自由水性质差异较大，不对称的未冻水膜厚度引起不平衡的渗透压力，导致未冻水从薄膜较厚处向较薄处流动，即水分持续从温度较高处向温度较低处迁移(Vignes-Adler，1977；Gilpin，1980)。随着Dash(1989)将热分子力概念引入冻土研究领域，认为分子间作用力使冰和土颗粒相互排斥，在未冻水膜上形成低压从而从周围吸水，才从分子力的角度系统地解释了水分迁移的驱动力来源，热分子力理论得以不断完善和发展(Wettlaufer，1999；Bronfenbrener et al.，2010; Rempel et al.，2001)。

现有研究对开放系统中水分迁移特征、影响因素及水分迁移驱动力已经有较为深入的认识，而忽略了封闭系统中由冻结引起的水分重分布，因此相关研究甚少。在中国沿海地区广泛分布高含水率、低渗透性的软土，当在深厚软土中采用人工地层冻结法施工时，由于土层较低渗透性的阻碍作用使得土层较难获得水源补给而主要发生内部水分迁移。相比于原位孔隙水相变产生的冻胀，土体内部水分迁移引起的冻胀量不可忽略。因此，本文通过室内封闭系统单向冻结试验，以冻结法施工中关键冻结参数——冻结温度为研究变量，对不同冷端温度下冻结锋面运移规律、冻胀量发展规律、水分迁移入流通量及速率特性进行研究，提出了水分迁移起始的判据，由此得到了封闭系统单向冻结试样内部水分迁移起始时刻的预测方法。本文研究结果对冻结法施工中的冻胀量预警具有重要参考价值，并为沿海软土地区冻结法工程设计提供了依据。

1 试验设备与方法

1.1 试验设备

试验设备主要包括单向冻结仪、低温冷冻液循环泵、应变式位移计、热电偶温度计、数据采集仪和计算机等。

单向冻结仪(图1)主要包括底座(冷端)、试样筒、顶盖、活动杆和外周保温材料。试样筒为空心圆柱形，由有机玻璃制成，高为190imm，内径为100imm，壁厚为10imm。在试样筒侧壁，距离底座顶面5imm、15imm、25imm、35imm、45imm高度处开有小孔，以方便热电偶线穿过试样筒插入试样内部。顶盖中心处钻有圆孔，铝制活动杆由圆孔穿入，活动杆底端与试样顶面的轻薄盖板接触，活动杆顶端与位移计接触。在试验过程中活动杆可垂向自由移动，试样冻胀量由活动杆传递至位移计。在试样筒外周和顶盖上部严密包裹保温材料，以阻隔试样与外部空气的热交换。

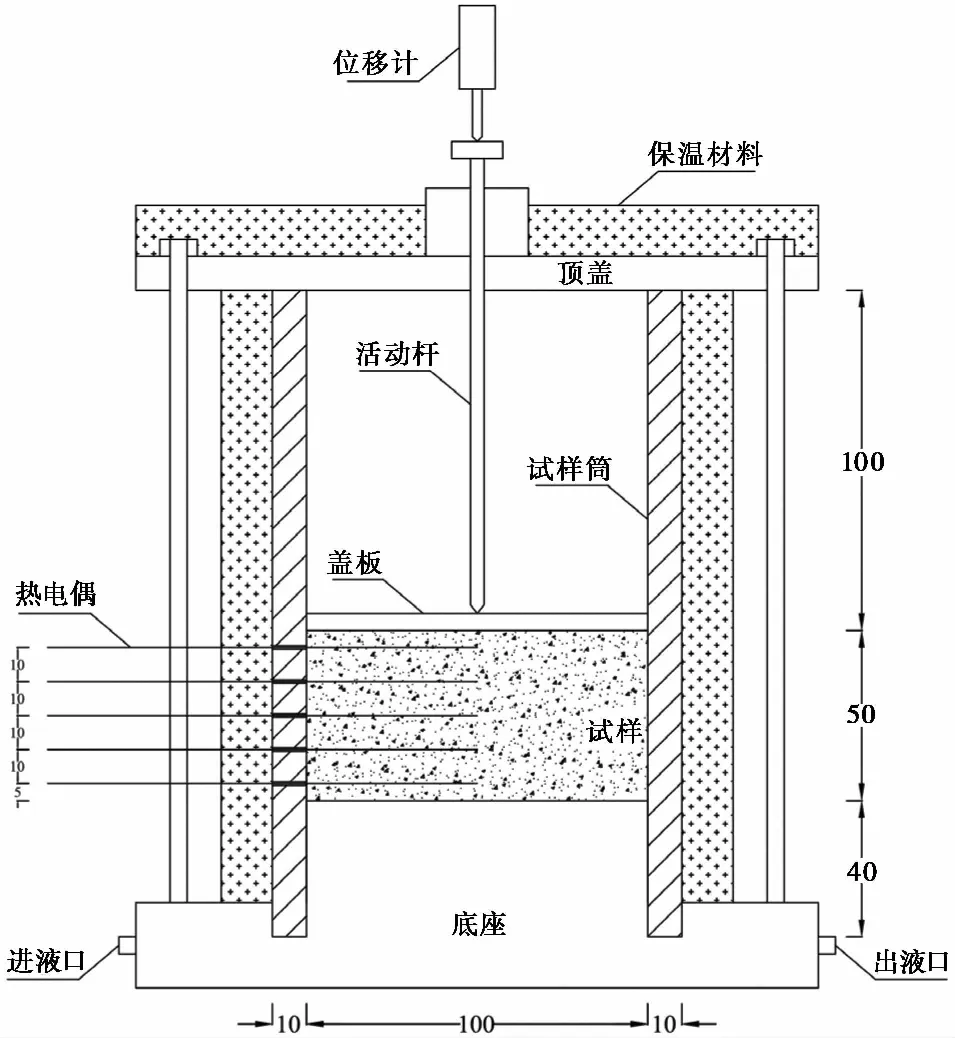
图1 封闭系统单向冻结仪及传感器示意图

1.2 试验方法

试验土样为上海第④层灰色淤泥质黏土，属第四系滨海-浅海相沉积层，具有高天然含水率、低渗透性等特性，土样基本物理性质见表1。将土样充分干燥后碾碎，用2imm孔径的筛子筛除杂质。取余下土粉与去离子水均匀搅拌至泥浆状，分层填入单向冻结仪试样筒内，填土过程中将泥浆充分捣实并排出气泡。通过预试验确定填土高度，填土完成后在土样顶面施加190ikPa(模拟9.5im深度处天然地应力)垂向荷载使土样固结。固结沉降稳定后土样高度为50imm，含水率约为49.8%。

表1 淤泥质黏土基本物理性质

制样完成后，移除垂向荷载使试样在冻结阶段自由冻胀。在试样顶面放置轻薄盖板，连接试验设备。开启低温冷冻液循环泵，使冷端初始温度恒定为1i℃。待试样初始温度稳定后，将冷端温度降低至目标温度(表2)，连续冻结12ih。

表2 冻胀试验条件

2 试验结果分析

冻结过程中实时记录距离冷端不同高度处的试样温度，使用二次多项式函数对测点温度与测点高度进行拟合，由此获得0i℃等温线(冻结锋面)高度随冻结时间的变化关系(图2)。

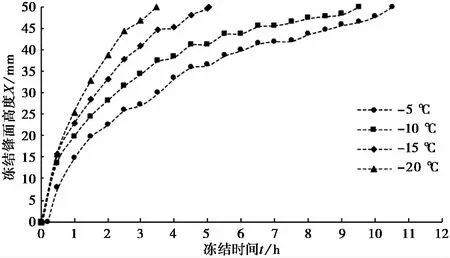
图2 不同冷端温度下试样冻结锋面高度

由图2可见，冻结锋面高度随冻结时间的延长而增大，冻结锋面推进速率逐渐减小。随着冷端温度的降低，冻结锋面推进至试样顶面(50imm)所需的时间缩短。在相同冻结时间下，冷端温度越低，试样冻结锋面高度越大。这是由于在试验过程中低温冷却液、冻结仪底座及试样组成一个热交换系统。低温冷却液与冻结仪底座发生热对流，冻结仪底座再与试样发生热传导使试样温度降低。在冷端初始温度下，系统热交换达到平衡，试样维持稳定的初始温度。当冷端降温至目标温度后，原先的热交换平衡被打破，系统热能排出量大于热能补给量，导致试样温度降低，冻结锋面持续推进。在冻结初期，冷端仅与其上部小范围试样进行热交换，热能排出量远大于热能补给量，试样温度迅速降低，因此冻结锋面推进速率大。随着冻结锋面的推进，热交换范围不断扩大，热能补给量增大，系统热交换向平衡状态过渡，试样降温速率减小，因此冻结锋面推进速率减小。当冷端温度降低，系统热能排出量增大，冻结锋面推进速率增大，因此在相同冻结时间下冻结锋面高度增大，且冻结锋面推进至试样顶面所需的时间缩短。冻结锋面高度随冻结时间的变化可由式(1)描述，不同冷端温度条件下拟合参数a、b的值见表3。

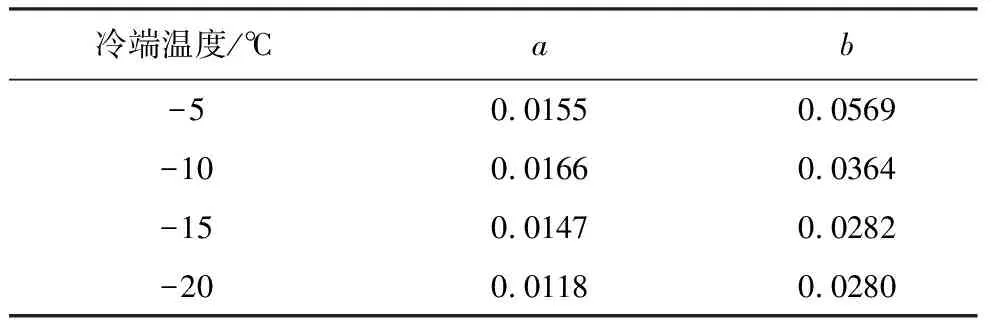
表3 拟合参数a、b取值

(1)

式中：X(t)为任一时刻试样冻结锋面高度(mm)；t为冻结时间(h)；a、b为拟合参数。

试样冻胀量与试样初始高度的比值为试样高度变化率(η)，不同冻结锋面高度下试样高度变化率如图3所示。由图3可见，在不同冷端温度条件下，试样高度变化率随冻结锋面高度的变化并非呈线性关系(图3中短划线参考线)。当冷端温度较高时(图3a)，高度变化率-冻结锋面高度趋势线(图3中圆点虚线)呈现典型“S型”曲线特征，即随着冻结锋面高度的增大，单位冻结锋面推进量下试样冻胀量先增大后减小。随着冷端温度的降低(图3b、图3c)，趋势线“S型”特征逐渐淡化，最终趋势线反弯点消失(图3d)。该现象表明在封闭系统中对淤泥质黏土进行单向冻结时，随着冻结锋面的推进，试样内部发生水分迁移，使得单位冻结锋面推进量下的试样冻胀量并非常数。

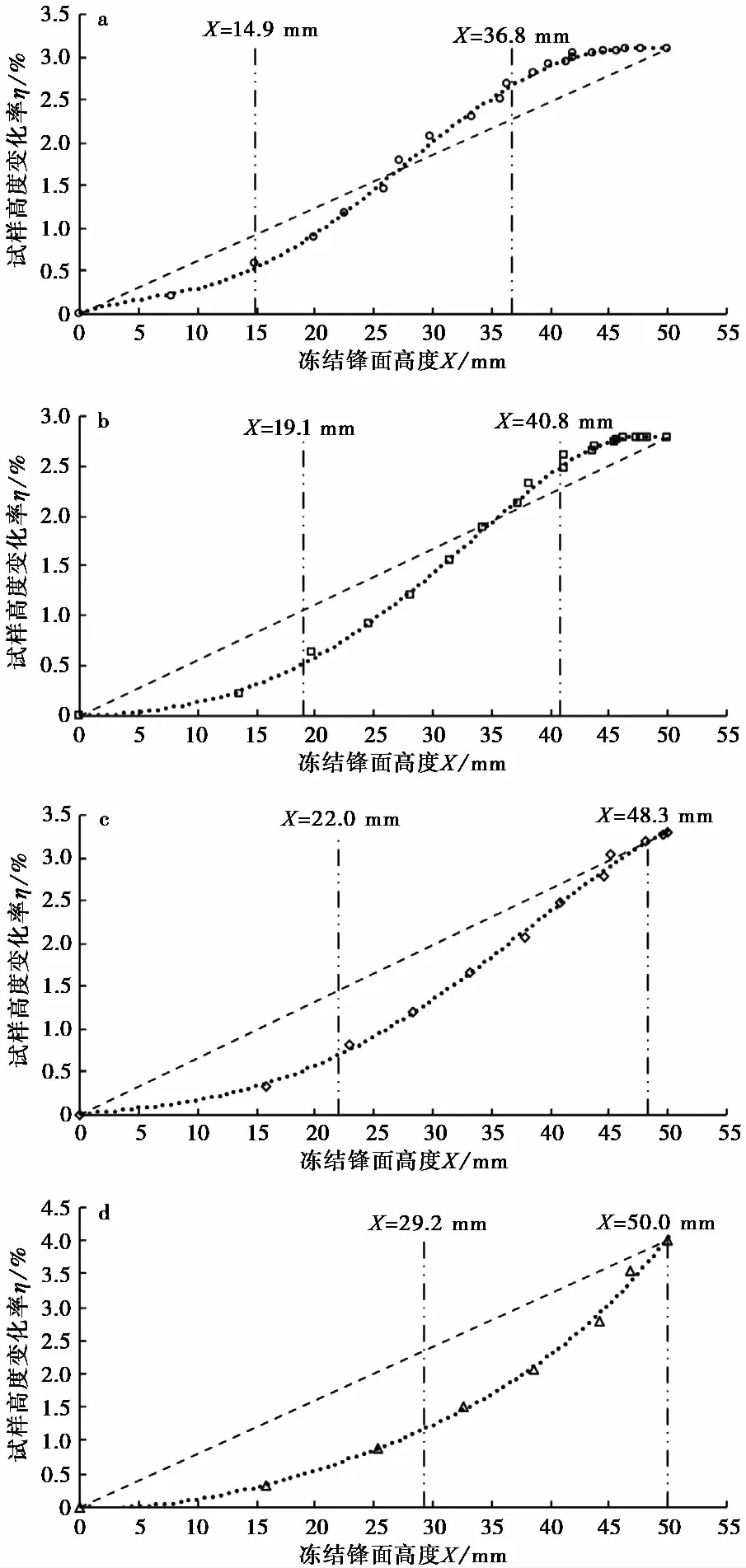
图3 不同冷端温度下试样高度变化率-冻结锋面高度关系

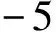
根据Konrad(1989)提出的分凝冻胀理论可知，单位冻结时间内试样分凝冻胀量远大于原位冻胀量，因此在试样内部发生分凝冻胀的冻结时间区间内可不考虑原位冻胀对总冻胀量的影响。通过冻结锋面的水分迁移入流通量由其高度表示(式2)，入流通量根据试样冻胀量由式(3)计算，将式(3)对冻结时间t求导即得入流速率。

(2)

(3)

式中：hw为通过冻结锋面的入流通量(mm)；mw为通过冻结锋面的迁移水质量(g)；ρw为未冻水密度(g·cm-3)；A为试样横截面积(cm2)；S为冻胀量(mm)。

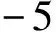
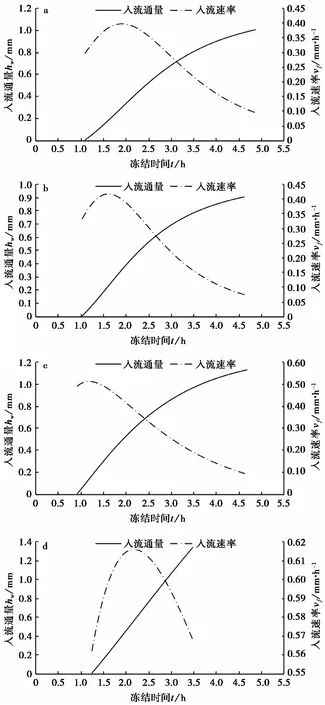
图4 不同冷端温度下入流通量及入流速率随冻结时间变化关系

根据图4中水分入流的起始时刻，由式(4)、式(5)分别计算得到该时刻不同冷端温度条件下冻结区与未冻区内的临界温度梯度。由于试样顶面为试样与盖板的材料分界面，若在此处安装温度传感器，其测定值将受到较大的环境干扰，因此本文采用接近试样顶面的45imm高度处试样温度值作为Tw代入式(5)。

(4)

(5)

式中：grad(T)1、grad(T)2分别为冻结区和未冻区的临界温度梯度(℃·cm-1)；Tc、Tw分别为冷端温度和暧端温度(试样顶面温度)(℃)；X(t)为任一时刻试样冻结锋面高度(mm)；H为试样初始高度，(mm)；S为冻胀量(mm)。

不同冷端温度条件下冻结区与未冻区内的临界温度梯度如图5所示。由图5可见，临界温度梯度与冷端温度具有良好的对应关系。随着冷端温度的降低，冻结区临界温度梯度线性增大，拟合公式为：grad(T)1=-0.3539T+1.3096；未冻区临界温度梯度呈指数形式增大，拟合公式为：grad(T)2=0.7043exp(-0.039T)。该关系式表明在封闭系统中对淤泥质黏土进行单向冻结时，可将临界温度梯度作为水分迁移起始的判据。在不同冷端温度条件下，当试样冻结区或未冻区温度梯度达到其相应临界温度梯度时，试样内部开始出现水分迁移。

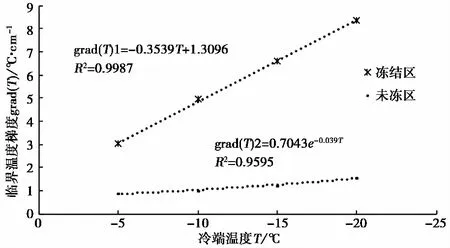
图5 不同冷端温度下的临界温度梯度

3 讨 论

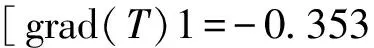
4 结 论

本文开展了不同冷端温度条件下封闭系统中淤泥质黏土单向冻结试验，研究了冻结锋面运移规律、冻胀量发展规律、水分迁移入流通量及速率特性，获得如下结论：

(1)在封闭系统中对淤泥质黏土进行单向冻结时，不同冷端温度下试样冻结锋面高度是关于冻结时间的函数，拟合公式形如：X(t)=t(at+b)-1。

(2)在封闭系统单向冻结过程中低渗透性、高含水率软土内部存在水分迁移现象，水分迁移起止时刻的冻结锋面高度均随冷端温度的降低而增大；水分迁移入流速率随冻结时间的延长先增大后减小，相应地，水分入流通量-冻结时间曲线随冷端温度的降低由“S型”逐渐趋于线性。

(3)试样冻结区内温度梯度降低至临界温度梯度是水分迁移起始的判据，临界温度梯度随冷端温度的降低而线性增大。

(4)结合临界温度梯度-冷端温度关系式和冻结锋面高度-冻结时间拟合公式，可预测某一冷端温度条件下封闭系统单向冻结过程中试样内部水分迁移的起始时刻。