在游戏中经历数学建模的过程
——以“点与数”的教学为例
朱燕锋,宋怡楠
(杭州市萧山区万向小学,浙江杭州,311215)
游戏除了娱乐还有什么功能?人在玩游戏时会沉浸其中,反复尝试着各种失败与成功,经历富有探索性的愉快过程。在数学游戏过程中,儿童可以更深刻地理解数学的内涵,感悟数学的思想方法,在获得灵活性、严谨性、发散性思维的过程中发展数学核心素养。数学游戏化学习就是把游戏思维和数学学习结合起来,在学中玩、玩中学,让游戏属于儿童,让数学帮助儿童成长。
进行数学游戏化学习的关键在于根据内容设计合适的数学游戏,从教学内容中提取可以发展的数学素养,从而在内容、目标与游戏之间建立联系。笔者在教学“点与数”时,为了让学生理解二进制与十进制的位值原理,选取棋子与方格作为游戏道具,制订了一定的规则,让学生在游戏体验中经历二进制建模的过程,在愉快的氛围中掌握一定的数学思想方法,锻炼思维的灵活性。
一、在观察发现中寻找数学模型
数学游戏根据教学内容的不同大致可以分成五种类型:熟悉操练型、观察发现型、策略感悟型、经验积累型、智能发展型。观察发现型的数学游戏指向数学规律的探究和发现,通过游戏感悟数学现象蕴含的数学原理。在“点与数”的教学中,笔者首先以棋子移动为点,不同方格为值,利用游戏让学生通过观察、比较、分析、推理的方式寻找长方形方格中点与数之间的规律,建构模型,并尝试运用模型去表示任意自然数。
(一)读图观察,寻找摆数规则
观察是学生学习的起点,简单的方格摆数游戏吸引了学生的注意力,给学生提供了学习数学的问题情境,让学生的眼、耳、口、手等多种感官系统参与其中,在读图观察中经历规则解读和规律探究的过程。
1.激趣导入,揭示课题
教师直奔主题,揭示课题“点和数”游戏,明确游戏规则:第一,每个方格里只放一颗棋子;第二,不同位置的棋子表示不同的数。教师在学生读懂游戏规则后,明确指出游戏玩法就是用棋子在方格图上摆出不同的数。
2.读图观察,探讨规律
《义务教育数学课程标准(2011年版)》指出:“要培养学生直接从图中搜集、分析和处理信息的能力。”因此,教师在教学中要培养学生学会从数学的角度观察画面,从中选择有用的数学信息,找出规律,解决问题。
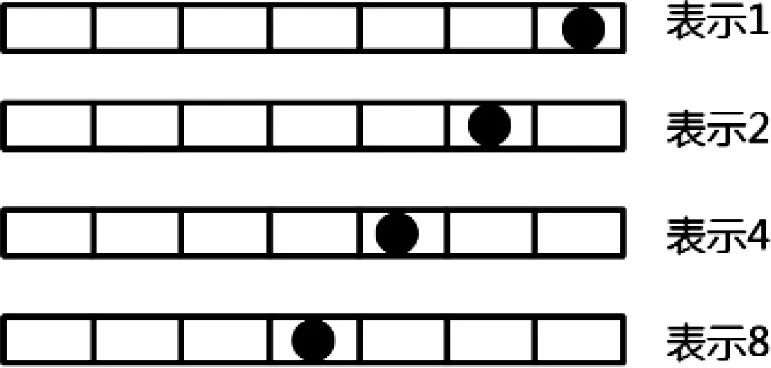
图1 摆数图
教师出示摆数图(图1),提问:“会玩这个游戏吗?我们一起来看看游戏摆数规律,你看懂了吗?”根据学生的回答,教师明确:把右边的数叫作前,左边的数叫作后,后一格的数=前一格的数×2。
师:能用算式表示上面的数吗?
生:1,1×2,2×2,4×2。
师:还能用其他方式表示这些数吗?
生:20,21,22,23。
师:用次方表示的,真厉害!如果把这个棋子放到第五格,表示几?你会怎么表示?
生:2×2×2×2。
师:我们还可以写成“24”,读作2的4次方。
数学模型是对实际问题的一种数学表述,读图之后对点的摆数规律的描述,开启了数学模型的探究。这时教师就要把这颗棋子放到第七格,引导学生观察它表示几,能否用算式表示。有部分学生说是32,因为第七格表示5个2相乘。教师依次数出第七格的位置,追问:“第七格到底是几个2相乘?”学生恍然大悟,第七个格子的点表示64,因为是6个2相乘。
(二)深究规律,初见模型
模型建立始于规律的探究过程,是在寻找更多规律中发现问题、寻找策略、形成解释、获得结论,亲历模型的形成过程。
1.再探规律,明晰方格数值
教师继续引导学生发现更多的规律并适时形成结构模型。学生在进一步探究中就会发现方格上的数等于2的格数减一次方。
师:99格上的数算式如何列?
生:98个2相乘。
师:200格上的数算式如何列?
生:199个2相乘。
师:第n格呢?
生:2n-1。
在教学中,教师不是盲目地带领学生去学习二进制,而是着重用位值的思想去玩这个游戏。对于能用这样简洁的方式表达这条规律、形成格子的数值理解的学生,教师要加以表扬。
2.对比发现,解读数值表示
学生读图观察,一个点的大小已经和对应方格上的数值建立联系,那么如何用更多的点来表示更多的数呢?这就需要学生进一步探寻、解读数值的含义。
教师出示图2并问学生又发现了什么。

图2 更多不同的数的摆数图
生:都是加起来的(多个点表示的数是所在点位置数的和)。
师:你能用算式来表示吗?
生:1+2=3,1+2+4=7。
教师明确可以组合不同位置的棋子表示更多不同的数,并进一步让学生辨析刚才用一颗棋子表示了8,那么8可不可以用多颗棋子表示?
生:8只有这一种摆法,因为右边三个格子最大只有7。
从一点到多点,利用点子与格子的位置关系建立大小关系,引导学生体验和感悟数学规律和思想。教师在教学中要着重引导学生理解位值的思想,让学生在对比中明白不同位置的方格代表不同的数,同一位置的方格代表相同的数,尤其是在出现进位时,如何顺利找到进位后的数所在的格。
二、在经验积累中分析数学模型
活动经验的积累对于分析数学现象、揭示数学本质尤为重要。学生在游戏活动过程中所获得的直接或间接的体验,是要靠学生经过反复实践、 独立思考、同伴互助、合作交流感悟出来的。学生在积极参与各种活动的过程中,完成了知识的学习和构建,真正地了解了获取知识的价值和意义。在教学中,笔者让学生在方格上用棋子摆各种数,找出方格背后二进制数的数值规律,如图3。

图3 “点和数”游戏现象和本质
(一)操作体验,交流策略
教师向学生讲明操作要求后,学生拿出信封中的棋子,在操作单上摆出自己喜欢的数。学生在操作体验后介绍自己的摆数方法。
教师投屏展示学生摆的数,与学生一起交流、分享,在摆数的时候标出每一格,帮助学生快速找到棋子表示的数。同时,教师还要求学生利用算式表示自己摆数的想法。
(二)分享经验,揭示本质
把数和形结合起来,就能够建立抽象的数学概念与形象的图形之间的联系。教师心中想一个数,如25,问学生会怎么摆,摆在哪里,用到几颗棋子。
生:因为25是奇数,所以要选1。
师:通过分析奇偶性你找到了1,16和8你是怎么找到的?
生:16+8=24。
师:哦,找到了这两个格子。那你们想16这个格子为什么要用到?说说你的理由。
生:16前面的格子全部加起来最大只有15,比16小1。16+8+1=25。
师:25太简单了哦,来个难的,252,想一想会在哪几格?会用到哪几颗棋子?
师:我发现了一个小细节,你们都没有看到呀!
生:我多画了一个格子。
数学教育家波利亚说:“学习任何知识的最佳途径都是由自己发现的。”在摆数活动中,学生发现7格不够。“不够是什么意思”的分析是学生对不同格子表示不同的位值的模型理解。在模型构建中,教师引导学生用不同的方法和角度来思考和解决问题。一开始,学生在格子上从右往左依次摆数,得出1+2+4+8+16+32+64+…,利用不断逼近的方法排除4来寻找252。也有学生用到十进制数中的凑整方法,先找到与252最接近的位值是256,右边7个格子的点数之和就是256-1=255,利用255-2-1=252。当然,也有学生先找128,再利用倒着算的方法得出128+64+32+…,从而不断寻找接近目标数的格子。教师在这个过程中,应引导学生观察、思考,发现其中的规律,把握数学本质,有效构建二进制位值的数学模型。
(三)再次活动,应用模型
摆数活动一:对于252想到了这么多方法,那么155你能不能想到好方法?比一比谁快。
方法交流:因为155-128=27,27-16=11,11-8=3,3-2=1,1-1=0,所以155=128+16+8+2+1。
摆数活动二:现在不比方法,比速度,比谁用最快的速度摆出125。
方法交流:因为128-1=127,127-2=125,125可以表示摆满右边6格减去第2格即可。
数学的发现和发展是一个应用的过程。模型思想注重数学的应用,即通过数学结构化解决问题。学生在数形结合中感悟数的大小关系,在灵活适切的教学活动中提升思维能力。学生在摆数中边摆边说自己的想法,在数的组成中通过有序思考,对二进制数位值的表示能力有了更大的提升,策略意识也逐步显现。
三、在智能发展中实现模型迁移
数学的本质是思维。学生在游戏的过程中因思维的发展而获得智能的进阶,可以说是数学游戏教学的目标与追求。在学生对游戏中的规律和位值有了初步理解,并建构了模型之后,教师有必要进一步深化教学方式,使学生在学习中学会灵活运用,举一反三,实现模型迁移。
如图4,教师出示另一种摆数图,引导学生仔细观察,四人小组在合作讨论摆数规律的基础上,再在操作纸上摆出自己心中的数,并进行交流。

图4 另一种摆数图
师:谁能上来摆一摆?猜一猜你摆的数表示几。(一学生上台,在最左边摆满4个棋子)
生:他摆的数是96。因为从右往左第一列每格表示1,第2列每格表示2,第三列每格表示6,第四列每格表示24,4格就是96。
师:这个摆数图和刚才的摆数规律不同,两者又有什么相同的地方?
生:从这两种摆数图中我们都可以表示出自己想要的数,而且每个数的表示方法只有一种,不会重复。
数学模型的解释和应用,不是将模型看作确定的算法或思维程序进行机械的记忆、复述与应用,而是将数学模型作为学生向更高层次跳跃的平台,为发展学生数学思维提供了更大的可能。在几颗棋子、几行格子变化的摆数挑战中,学生的观察能力、迁移能力、逻辑思维能力等空间智能都得到了充分的提升。看似简单的游戏操作,却蕴含丰富的数学思考,最重要的是能让学生通过数学游戏充分体验学习与生活。这不仅可以提高学生学习数学的兴趣,而且有助于学生对进制的理解,使学生在内心建立认知模型并发展数学核心素养。
学生认识事物要经历由易到难、由直观到抽象、由感性认识上升到理性认识的过程。数学游戏课就是引导学生从易到难、由浅入深的切入口,必须有趣、鲜活。基于核心素养培养的“点与数”教学,让学生在操作体验中经历数学模型建构,把握数学所学知识的过程。我们期待学生用眼睛观察、用耳朵聆听、动手操作、动脑筋思考,多感官协调学习,在数学游戏中了解数学的本质,爱上数学。

