多种因素影响下的船舶航线诱导模型构建与应用

张 赫, 闫建鑫, 邢江豪

(大连海事大学交通运输工程学院， 大连 116026)

随着世界经济和技术的快速发展，各种类型船舶的数量随之持续增加，船舶之间交通冲突和拥挤的现象愈发严重。例如海上船舶在行驶到工程船舶的作业区域时，大量的工程船舶根据作业地点的不同需要多次穿越航道，这与往来正常航行的其他船舶形成了一个复杂的航线网络，船舶的航行受到极大的影响。在这种情况下，需要对船舶的行驶路线进行合理规划，而诱导技术是实现路径优化的有效方法之一。

路径诱导技术自20世纪产生到现在已经几十年的历史，相关的资料也比较完善，目前更多的应用于车辆行驶的诱导。对于汽车的路径诱导中外相关领域的专家采用不同方式和方法进行了大量研究[1-4]，而针对于船舶的诱导研究较少，仅有乔春福[5]研究了如何根据船位序列判断船舶上行和下行的算法，从而为过往船舶的上下行助航提供诱导帮助。从文献中可以看出，目前对船舶的航线诱导还在发展之中，仅有的研究也只是考虑了行驶水域的特点结合地图进行上下行的助航，没有针对于某一船舶在复杂的水域内行驶的航线诱导。而陆上汽车的路径诱导问题经过多年的发展已经趋于成熟，相关理论也相对完善，这对实现船舶的航线诱导具有指导意义。现在考虑与陆上汽车诱导所不同的气象水文条件影响的基础上结合船舶航行的特点将诱导技术运用到船舶的航线规划之中，以期为船舶航行提供科学依据。

1 海况对船舶航行的影响

船舶在海上航行时，空气和水对船舶行驶具有很大的影响，为了便于研究船舶在不同的风浪条件下的行驶速度，将船舶阻力分为基本阻力、空气阻力、汹涛阻力三部分。

1.1 基本阻力

船舶基本阻力是船舶在静水中航行受到的阻力，由摩擦阻力和压阻力(剩余阻力)组成。结合傅汝德相似定律和雷诺相似定律可得船舶静水行驶基本阻力R0的计算表达式[6]：

(1)

CR=Cf+ΔCf+Cr

(2)

式中：CR为基本阻力系数，ρ0为流体密度，V0为船舶在静水中的行驶速度；S为船舶湿面积；Cf为船舶摩擦阻力系数；ΔCf为粗糙度补贴系数；Cr为船舶剩余阻力系数。

摩擦阻力系数Cf用“1957年国际船模实验池实船-船模换算公式”[式(3)]进行求解, 粗糙度补贴系数ΔCf如表1所示；剩余阻力系数Cr利用Lap-kelller图谱进行查表计算获得[7]。

(3)

(4)

式中：Re为雷诺数；V为船速；Lwl为水线长，近似于船长L；ν为水运动黏性系数。

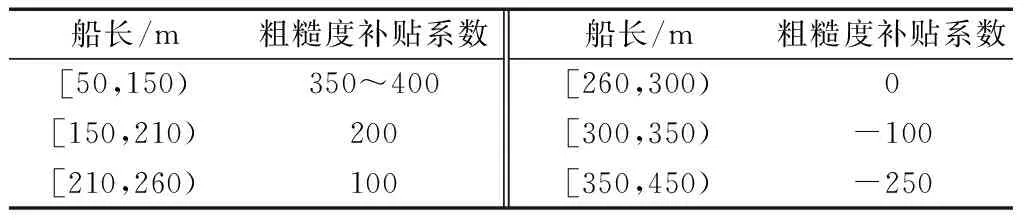
表1 粗糙度补贴系数Table 1 Roughness subsidy coefficients

1.2 空气阻力

船舶在海上航行时，其水面以上的部分在风的作用下会产生空气阻力影响行驶速度，产生船舶艏艉方向的风压力Fw可按式(5)计算[8]：

(5)

(6)

(7)

(8)

lgY=αw+βwlgX

(9)

式中：ρa为空气密度(1.226 kg/m3)；Cw为艏艉方向上风力系数；Va为相对风速；Aa为水线以上船体正面受风面积；Ba为水线以上船体侧面受风面积；Vzf为真风风速；αa为真风方向角，左舷为正；θ为风舷角；Ca为风力系数；α为风力角，是风压力与船舶艏艉线之间的夹角；Y为船舶受风面积(包括Aa、Ba)；X表示船舶载重量或总质量，t；αw、βw为回归系数，其数值如表2所示[9]。

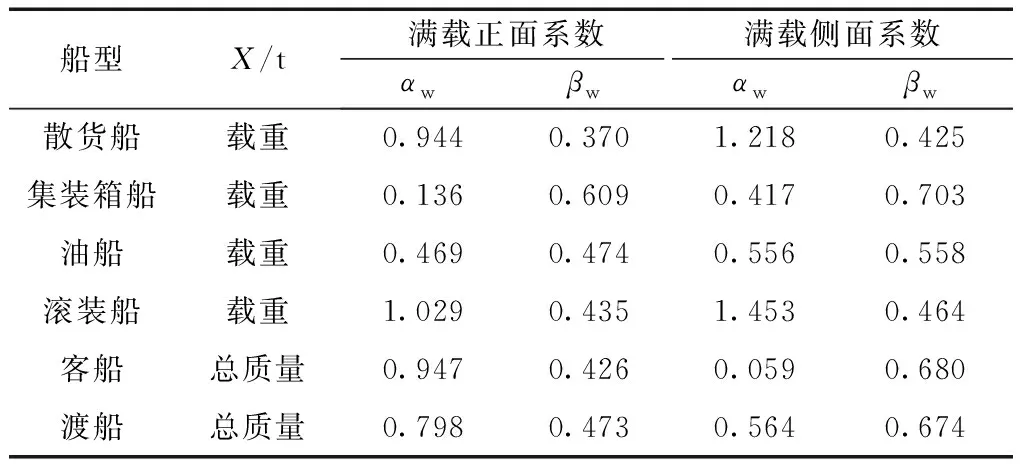
表2 不同船型船舶的受风面积回归系数Table 2 Regression coefficient of windage area of different types of ships

风力角α和风力系数Ca可根据岩井聪公式[式(10)和式(11)]进行计算[6-8]：

(10)

Ca=1.325-0.05cos(2α)-0.35cos(4α)-0.175cos(6α)

(11)

1.3 汹涛阻力

汹涛阻力分为规则波干扰和不规则波干扰两种，通常只考虑规则波的影响。对于规则波干扰力的计算比较复杂，目前主要依靠船模实验进行，Daidola在船模实验的基础上提出了汹涛阻力的计算模型为[6-7]

(12)

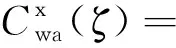
(13)

1.4 船舶自由行驶速度

假定船舶在静水中行驶的推进功率和风浪中行驶的推进功率保持不变，则船舶在风浪中行驶减少的速度用来抵消风浪阻力的影响[6]，从而得到船舶在风浪下自由航行速度Vf。

(14)

由于船舶在不同路段行驶的位置和方向并不一致这就导致相对风速的大小、方向发生变化，因此船舶在不同路段行驶时自由航行速度Vf需要根据行驶方向和位置分别求解。

2 路段行程时间计算

在对船舶进行航线诱导时，优化目标通常有距离、时间和费用三种，通过综合考虑，现以航线用时最短作为优化目标。

各路段行程时间分为路段行驶时间和航线网络交叉点延误时间两个部分。在没有航线交叉的路段内，路段行程时间就等于路段行驶时间。船舶在路段的行驶时间与路段船舶流量密切相关，根据风浪对船舶航行的影响对美国联邦公路局函数即BPR函数进行改进，建立路段行驶时间的表达式：

(15)

式(15)中:tx为两节点之间路段行驶时间；ψ为风浪对航速的影响系数，ψ=Vf/V0；t0为两节点之间交通量为零时无风浪影响下的路段行驶时间；q为路段船舶交通量；c为航路实际通行能力；γ1、γ2为相关系数。

航线交叉点平均延误时间td根据排队论原理进行求解。将船舶看作“顾客”，交叉点视为“服务窗”，船舶在交叉点的排队穿越过程可视为一个排队问题。船舶到达交叉点时，若“服务窗”被占用，则进行排队等待，最大排队长度n为航道长度和单位船舶所需的航道长度Ld的比值。对船舶到达规律进行统计分析，船舶的到达规律可近似服从参数为λ的泊松分布，船舶通过交叉点的服务时间可看作服从参数为μ的负指数分布(到达率λ=q,μ可统计获得)[10]。因此交叉点的船舶排队模型为M/M/1/n/∞模型。

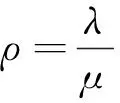
(16)

综上，ij路段总行程时间tij为

tij=tx+td

(17)

3 模型构建

3.1 影响因素分析

3.1.1 施工水域影响

在海上航行的船舶可能会遇到海上施工区域，影响船舶航行。由于施工区域内有大量工程船舶进行运输作业，使得施工区内航线密集，交叉增多。

3.1.2 海风动态变化

船舶位置不同，船舶受到风力大小也不一致，为此建立船舶风速与位置的对应关系公式Vzf=φ1Vfe，其中φ1为与位置相关的风力作用系数(0≤φ1≤1)，Vfe为基本风速。

3.1.3 波浪动态变化

波浪振幅的变化与海风息息相关，并且影响汹涛阻力的大小。为此建立波浪振幅与位置的对应关系公式Wa=φ2W0，其中φ2为与位置相关的波浪作用系数(0≤φ2≤1)，W0为基本波浪振幅。

3.1.4 沉点的影响

对船舶航行产生阻碍的物体所在的位置称为沉点。在施工区域内，进行挖泥、疏浚作业的船舶通常移动速度较慢可视为沉点，若沉点存在于路段中相应路阻为无穷大。浅滩、岛屿等存在的位置也是沉点，为禁止行驶区域需绕开行驶。

3.2 模型建立

在对船舶航线诱导时，将航线网络抽象成图论网络G=(P,E,T)，其中P是节点集合表示航道节点；E是弧的集合表示路段；T={tij(Ti)|(i,j)∈E}是各弧的权值，表示在此路段的行程时间tij(Ti)为船舶在Ti时刻从节点i航行到节点j所需花费的时间。设施工区k(k=1,2,…，l)的节点集合为Pk存在的时间为[Tks,Tke]，从起点到达施工区k的时间为tk，非施工区节点结合为P0。则建立船舶动态时变网络下的船舶航线诱导优化模型为

(18)

s.t.

(19)

(20)

(21)

(22)

(23)

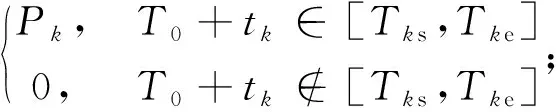
k=1,2,…,l

(24)

(25)

Vzf=φ1Vfe

(26)

Wa=φ2W0

(27)

式(18)为优化目标；式(19)表示路段ij在时刻被路径使用则等于1，否则等于0；式(20)表示初始点只能是出发点不能是到达点，终点只能是到达点不能是出发点，中间节点的到达和出发次数相等；式(21)表示所有路段最多只能被选择一次；式(22)为施工区内沉点对行程时间的影响；式(23)、式(24)表示船舶行驶到施工区域位置时若在施工区域存在的时间范围内则将区域内节点加入到航线网络之中，否则保留原节点；式(25)表示船舶各路段自由行驶速度的计算；式(26)为风速与位置的对应关系式；式(27)为波浪振幅与位置的对应关系式；行程时间计算过程中的其他参数的计算公式约束第1节与第2节已经说明，此处不再列出。

对于各路段船舶流量进行实时的更新是非常困难的，通常将时间根据实际划分为多个时段，并假定在同一个时段航路网各路段的船舶流量不发生改变。

4 蚁群算法求解

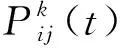
(28)

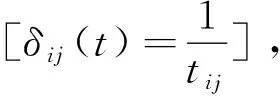
蚂蚁释放在各节点之间的信息素随着时间的流逝也会逐渐消失，设参数ε3(0<ε3<1)代表信息素的挥发系数。当m只蚂蚁都完成了一次循环后，需要对各节点间t时刻的τij(t)进行迭代更新，公式为

(29)

(30)

式(30)中：Q为蚂蚁在一次循环中所散发的信息素总量；Lk为第k只蚂蚁在本次循环中所花费的总时间。

针对于本文航线诱导问题，以船舶出发点为蚂蚁路径起点o，以船舶目标点为蚂蚁路径寻找的终点，以蚂蚁选择的节点集合表示船舶路径的可行解。假设初始时刻T=T0,则用蚁群算法求解的基本过程如下：

(1)对蚂蚁总数目m、信息素影响因子ε1、启发函数影响因子ε2、信息挥发因子ε3、迭代次数t、最大迭代次数tmax等参数进行设置,令初始时刻m只蚂蚁所在节点x=o。

(2)根据生成的施工区域和各节点的坐标，计算各节点间的行驶方向和风浪的相对大小和方向。

(3)根据气象水文条件和船舶本身状况计算船舶在各路段的自由行驶速度Vf，并据此求出对应的风浪影响系数。

(4)蚂蚁根据与x相连的可行解节点在T时刻的船舶流量和风浪影响系数等计算从节点x到可行节点各自的行程时间，然后按照式(28)依概率选择下一节点。

(5)令T=T+Txr(r为选择的下一节点，Txr为路段xr行程时间)、x=r，返回(4)继续选择下一节点直到到达目标点。

(6)蚂蚁k(k=1,2,…,m)到达目标点则按照实际用时记录此路径，依次完成所有m只蚂蚁循环，记录此次迭代中的最优路径及用时，并按照式(29)对信息素进行更新。

(7)令t=t+1,x=o,T=T0若t≤tmax转向(4),进行下一次迭代，否则转向(8);

(8)输出最优解。

5 算例

在此给出如图1所示的从烟台到天津的简易模拟航线路网(箭头表示只能单向通行)，阴影区域为沉点存在的区域，用MATLAB编程求解。利用随机算法在航线网络中随机生成3个长度为6～8 km的互不影响矩形施工区域，施工区域存在的时间为[T0+Xk,T0+Yk](0≤Xk≤Yk≤24 h)。在各施工区域内随机生成一个施工船沉点，若沉点在航线路段当中，则该路段行驶时间为无穷大，以15 min为一个时段。

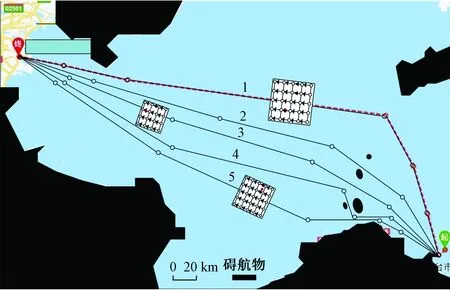
图1 模拟航线网Fig.1 Analog ship route network

设置起点的标号为0，终点的标号为1 000，1号航线的各点标号为101、102、103、104、105，同理为其他各航线进行标号。图1中在1、3、5航线内生成的施工区航线网络及相应标号分别如图2(a)～图2(c)所示。

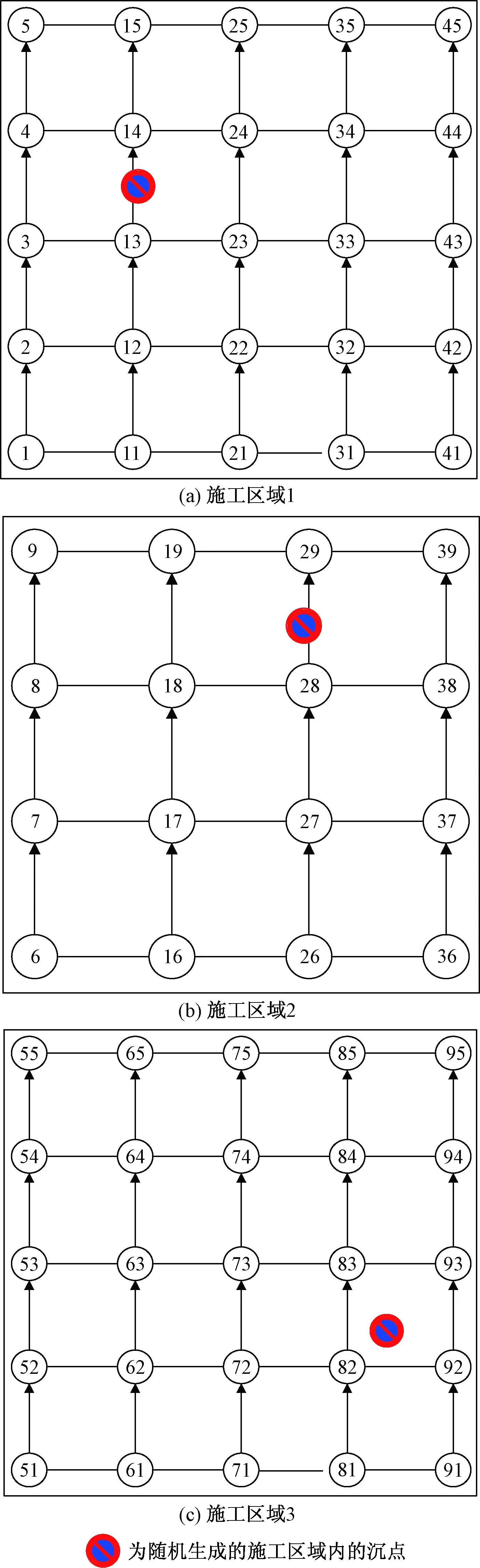
图2 海上施工区域航线网络Fig.2 Route network in offshore construction area

现选择某型号散货船进行计算，该船舶船长180 m，船宽32.2 m，载重量为48 103 t，满载排水量54 385 t，吃水11.6 m，静水营运航速为6.5 m/s，真风方向为西偏北30°，波长取0.8倍船长。

在用蚁群算法求解时，取m=30,ε1=1,ε2=1,ε3=0.1,tmax=200, 求得时变网络中各代最短用时和平均用时随迭代次数的变化曲线如图3所示。

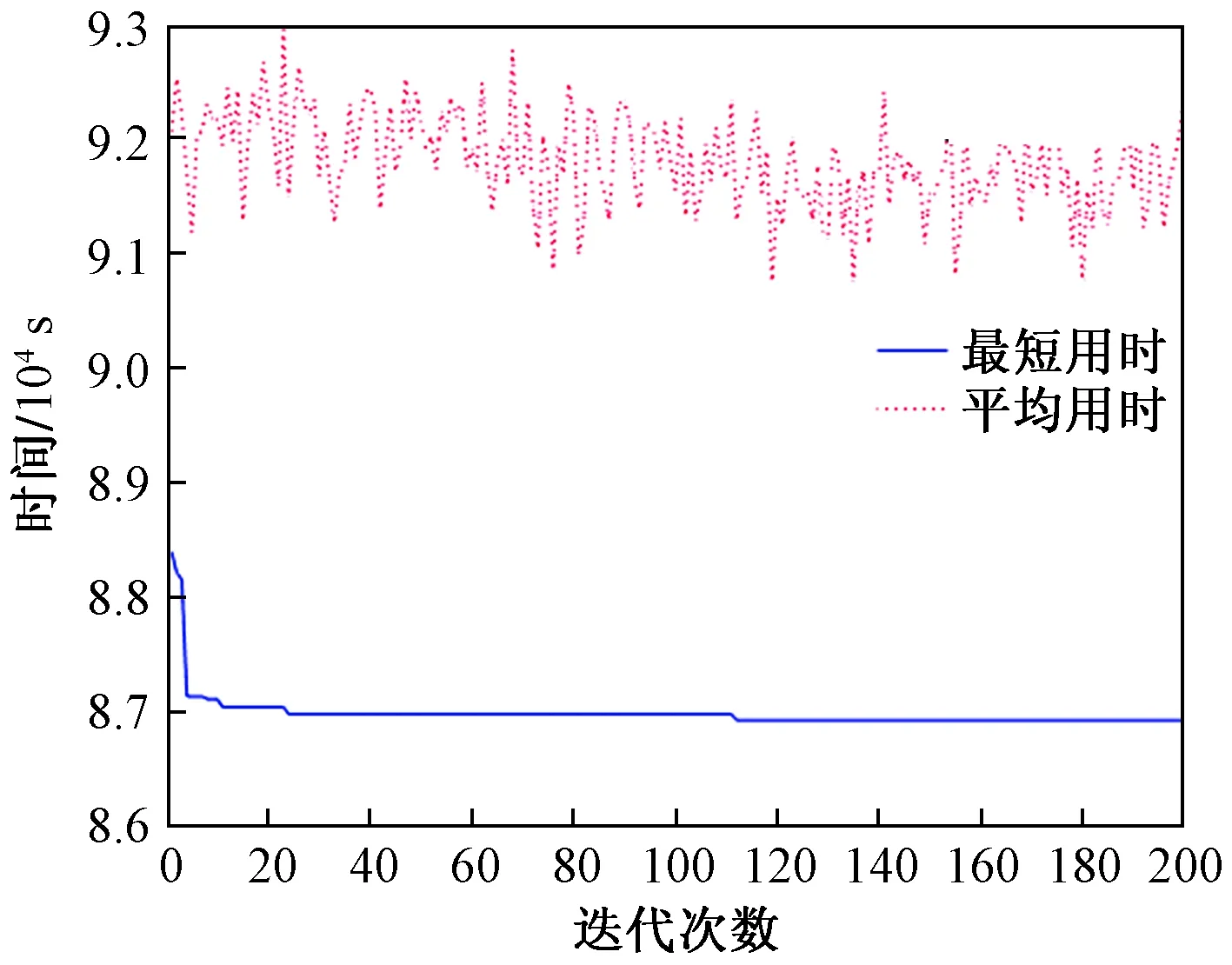
图3 时变网络各代最短用时和平均用时对比Fig.3 Comparison of shortest and average time of each generation in time-varying networks

最终通过MTALAB编程求得动态网络的最佳路径为0→501→502→503→71→81→91→92→93→94→95→504→505→1 000，用时86 937 s。在相同情况下，求得1、2、3、4航线的最短用时分别为90 958、91 704、91 818、92 504 s。最佳路径比4航线路径少用时5 567 s,减少用时6.4%。

6 结论

通过建立船舶的航线诱导模型利用MATLAB软件进行算例仿真验证，说明了本文提出的船舶航线诱导方法能为船舶在复杂航线网络下行驶提供航行路线决策帮助，可以得出以下结论。

(1)减少总用时时间。通过算例将求解的路线与其他路线的最优结果进行对比，结果表明在此次算例中最佳航线比其他航线最优结果最高可减少用时6.4%，证明了船舶动态航线诱导的更优性和模型的可行性。

(2)提高模型适用性。充分考虑了海上船舶航行的特点，在建模时考虑施工水域的影响、海风和波浪的动态变化影响以及沉点的影响，对路段行驶时间求解时对BPR模型进行改进并结合排队论的理论，使得模型比以往更加适用于船舶。

当前模型与实际情况还有些区别，缺乏对突发情况的考虑，风浪对船舶的影响的计算也还不够精确，这是今后改进的方向。