地球卫星重力场模型及其应用研究进展

吴庭涛, 郑 伟,3,4,5,6,7*, 尹文杰, 张捍卫, 张刚强, 张文松

(1.河南理工大学测绘与国土信息工程学院， 焦作 454000； 2.中国空间技术研究院钱学森空间技术实验室， 北京 100094；3.辽宁工程技术大学测绘与地理科学学院， 阜新 123000; 4.太原理工大学大数据学院， 晋中 030600;5.南京航空航天大学航天学院， 南京 210016; 6.电子科技大学航空航天学院， 成都 611731; 7.东南大学仪器科学与工程学院， 南京 210096)

地球重力场是地球的基本物理特性之一，反映了地球内部物质的空间分布及其运动变化，同时决定着大地水准面的起伏和变化，研究地球重力场及其时变是人类更深层次认识地球的必由之路[1]。高精度和高空间分辨率的地球重力场模型为人类探寻自然资源、揭示环境变化和预测自然灾害提供了重要的基础信息，尤其是高精度地球时变重力场模型在全球陆地水文变化、冰川消融与海平面升降、强地震分析和气候变化等方面具有重要意义[2-7]。

高精度和高空间分辨率的地球重力场测量在国际上一直受到高度重视。传统的重力测量手段主要有地面重力测量和航空重力测量，由于受到地形、天气等自然条件和作业强度、成本等人工条件的限制，覆盖率并不理想，一般只能用于区域重力测量。卫星测高受限于测量区域地面反射性要求，一般只能用于海洋和冰川地区重力场测量。而卫星重力测量不受地面环境和天气状况等条件限制，自动测量重力场数据，为获取的全球高精度、高空间分辨率的地球重力场模型及其时变提供了新的路径[8-9]。目前国际上已进行了四期地球重力卫星任务，即挑战小卫星有效载荷计划(challenging minisatellite payload, CHAMP)、地球重力场恢复及气候探测计划(gravity recovery and climate experiment, GRACE)、地球重力场稳态海洋环流探测计划(gravity field and steady-state ocean circulation explorer, GOCE)和下一代地球重力场恢复及气候探测计划(gravity recovery and climate experiment follow-on, GRACE-FO)。国际上公开发布的融合卫星重力测量、地面/航空重力测量和卫星测高等数据的高精度地球重力场模型最高可达2 190阶，如美国国家地理空间情报局(US national geospatial-intelligence agency, NGA)释放的全球超高阶地球重力场模型EGM2008(earth gravitational model 2008)，德国波兹坦地学研究中心(German Research Centre for Geosciences Potsdam, GFZ)和法国空间大地测量组(groupe de recherche de géodésie spatiale, GRGS)联合发布的全球超高阶地球重力场模型EIGEN-6C4等，已经具有相当高的应用价值[10-11]。

尽管目前地球重力场反演已经取得了部分进展，但对于彻底理解地球重力场及其应用仍远远不足，地球重力场的反演仍然是大地测量学和地球物理学的重要基础研究领域。中国在重力测量方面起步较晚，目前还没有自主发射的重力测量卫星，但在地球重力场反演研究方面已取得了一系列成果，如中国科学院测量与地球物理研究所的IGG系列和WHIGG-GEGM01S/02S/03S系列模型，武汉大学的WDM系列模型、西安测绘研究所的DQM系列模型及同济大学的Tongji系列模型等。

自2002年第一颗重力卫星CHAMP发射以来，中外研究人员围绕四期地球重力卫星任务开展了大量研究。2017年，GRACE卫星运行15年后结束使命，2018年，GRACE-FO卫星发射。在这个承前启后的时间点，对前人在地球重力卫星方面的研究进展进行总结和回顾并提出未来展望是非常有必要和意义的。

1 卫星重力测量的基本概念与发展历程

1.1 卫星重力测量的基本概念

卫星重力测量主要分为卫星跟踪卫星和卫星重力梯度测量两种技术[12]。如图1、图2所示，卫星跟踪卫星技术是利用高轨或低轨卫星跟踪另一低轨卫星由于地球重力场引起的卫星轨道摄动，再由卫星轨道摄动反演地球重力场模型，包括：卫星跟踪卫星高低模式(satellite-to-satellite tracking in the high-low mode, SST-HL)和卫星跟踪卫星低低模式(satellite-to-satellite tracking in the low-low mode, SST-LL)。如图3所示，卫星重力梯度(satellite gravity gradient, SGG)测量技术是利用低轨卫星搭载的重力梯度仪测量卫星轨道高度处的重力梯度张量，进而反演地球重力场模型。

图1 卫星跟踪卫星高低模式测量原理Fig.1 SST-HL measurement theory

图2 卫星跟踪卫星低低模式测量原理Fig.2 SST-LL measurement theory

图3 卫星重力梯度测量原理Fig.3 SGG measurement theory

1.2 卫星重力测量的发展历程

自1957年苏联在世界上首次成功发射人造卫星Sputnik-1以来，利用卫星观测资料建立地球重力场模型的理论和方法在过去的60年中得到迅速发展，并由此衍生了卫星重力学[13]。

20世纪60年代，Baker[14]和Wolff[15]相继提出卫星跟踪卫星高低模式(SST-HL)和卫星跟踪卫星低低模式(SST-LL)理论，为后续卫星重力测量任务实施提供了理论支撑。1969年，Kaula[16]基于卫星轨道摄动理论，首次结合地面跟踪卫星轨道观测数据和地面重力观测数据构建了8阶地球重力场模型，为卫星重力学奠定了基础。

20世纪70—80年代，美国和欧洲相继提出基于卫星跟踪卫星模式的卫星重力测量方案，并进行了相应实验验证可行性。20世纪80年代末，欧空局(European Space Agency, ESA)率先提出发射搭载非保守力补偿系统和重力梯度仪的低轨卫星来进行卫星重力梯度测量实验，随后，美国国家航空航天局(National Aeronautics and Space Administration, NASA)也提出卫星重力梯度测量计划。

虽然通过低轨卫星测量地球重力及其变化的概念最早在20世纪60年代已经提出，但直到20世纪90年代，随着GNSS技术已经成熟到能够精确对卫星进行定轨，重力卫星计划才真正进入实施阶段。2000年以后，随着CHAMP、GRACE、GOCE和GRACE-FO四期地球重力卫星任务相继成功实施，地球重力场探测进入了新纪元。卫星重力测量发展史如表1所示。

1.3 地球重力卫星

CHAMP卫星是由德国GFZ提出并负责研制，是世界上第一颗重力卫星，于2000年7月15日在俄罗斯发射，CHAMP卫星如图4所示。CHAMP卫星设计寿命5年，通过四次轨道提升实际运行10年，绕地球飞行58 277周，为地球科学研究提供了大量重力观测数据[17]。CHAMP卫星采用稳定的梯形结构以保证内部空间的平稳，卫星搭载有用于精确定轨的BlackJack型双频全球定位系统(global positioning system, GPS)接收机系统，精度约为10 cm；测定卫星所受非保守力的STAR加速度计，精度约为1×10-9m/s2；测定卫星与地面激光测距站之间距离以验证GPS观测数据的激光反射镜，精度为1～2 cm；提供高精度卫星姿态参考的恒星敏感器，精度约为4″。CHAMP采用卫星跟踪卫星高低模式(SST-HL)，空间分辨率为1 000 km时大地水准面差距约为1 cm，重力异常为0.02 mGal，极大改善了长波重力场模型的精度。CHAMP任务的科学目标：①从轨道摄动分析中得到全球长波至中波长的静态和时变地球重力场模型，用于地球物理学(固体地球)、大地测量学(大地水准面)和海洋学(洋流和气候)；②全球地球磁场反演，应用于固体地球物理研究；③利用GPS无线电掩星技术探测大气和电离层环境，应用于天气预报、导航和全球气候变化[17]。

表1 卫星重力测量发展史[12]Table 1 History of satellite gravity measurement[12]

图4 CHAMP卫星示意图Fig.4 Sketch of CHAMP satellite

GRACE任务由美国NASA和德国宇航中心(German Aerospace Center, DLR)合作研发，是国际上首次采用卫星跟踪卫星低低技术(SST-LL)的重力卫星任务。GRACE卫星如图5所示。GRACE由GRACE-A和GRACE-B双星组成，在485 km的轨道高度上相距220 km，其设计寿命为5年，实际运行时间长达15年，为地球重力场模型反演做出了不可磨灭的贡献[18-19]。卫星搭载有测定星间距离/速率的高精度星间微波测距系统(K-band ranging, KBR)，精度为1 0 μm/s；用于精确定轨的BlackJack型双频GPS接收器系统，精度约为5 cm；用于提供GRACE卫星所受非保守力数据的SuperSTAR加速度计，精度为3×10-10m/s2；提供高精度卫星姿态参考的恒星敏感器，精度约为2″。GRACE采用卫星跟踪卫星高低/低低(SST-HL/LL)模式，通过高轨GPS卫星跟踪低轨GRACE双星以及GRACE双星前后相互跟踪来联合确定地球重力场，空间分辨率为275 km时大地水准面精度为1 cm，重力异常精度为0.02 mGal，相比CHAMP具有显著提高[20]。GRACE任务的科学目标：①以前所未有的精度和分辨率获得地球重力场模型及其时间变化；②利用GPS无线电掩星技术获得全球的大气垂直温度和湿度剖面图；③为研究海洋洋流、冰盖和冰川质量变化和大陆水和雪的存储变化等提供高精度时变重力场模型。

图5 GRACE卫星示意图Fig.5 Sketch of GRACE satellite

GOCE是世界上首颗采用重力梯度测量模式(SGG)的卫星，由ESA独立研制，GOCE卫星如图6所示。GOCE卫星设计寿命20个月，实际在260 km轨道高度上飞行4年8个月，为提高地球中短波重力场模型精度提供了海量观测数据[21-23]。GOCE卫星搭载高精度重力梯度仪，可直接测定卫星轨道高度处的引力位二阶导数，精度达3×10-12m/s2；用于非保守力补偿系统的离子微推进器，精度为50 μN；用于提供卫星姿态参考的恒星敏感器，精度约为1″；用于确定卫星轨道的GPS/GLONASS复合接收机，精度为2 cm。GOCE卫星通过结合卫星跟踪卫星高低模式(SST-HL)和卫星重力梯度测量模式(SGG)来确定地球重力场，并首次搭载了非保守力补偿系统来平衡非保守力(包括大气阻力、太阳辐射压、地球辐射压、卫星姿态控制力等)，当空间分辨率为100 km时，大地水准面误差为1～2 cm，重力场异常误差约为1 mGal[24-25]。GOCE任务的科学目标：①确定高精度和高空间分辨率的中短波地球重力场；②首次探测地核结构，为更好地了解地球内部物理结构提供新的资料；③联合卫星测高提供一个精确的海洋大地水准面，满足海洋环流、海洋热循环等研究的需要。

图6 GOCE卫星示意图Fig.6 Sketch of GOCE satellite

GRACE Follow-On(GRACE-FO)卫星由NASA和GFZ共同发起研制，卫星于2018年5月22日发射，其任务主要是保持GRACE的数据连续性，最大限度地减少GRACE之后的数据缺失。GRACE-FO卫星如图7所示。GRACE-FO卫星搭载实验性质的激光测距干涉仪(laser ranging interferometer, LRI)，测量精度相比上一代的星间微波测距系统提高约20倍，其他科学载荷与GRACE卫星并无太大差别[26-27]。GRACE-FO任务的科学目标：①继续GRACE任务的高分辨率地球重力场月模型反演，预计寿命为5年；②验证激光测距干涉仪在改进卫星跟踪卫星低低模式(SST-LL)测量性能方面的有效性;③继续进行GPS无线电掩星测量，以便为气候提供服务(例如大气垂直温度/湿度剖面图)。一般认为，当前GRACE-FO任务只是为了避免地球重力观测数据出现较长时间断层而进行，而非真正意义上的下一代重力测量卫星。国际上预计的下一代GRACE Follow-On卫星轨道高度为250 km，星间距离50 km，同时搭载非保守力补偿系统和激光干涉测距仪，反演地球重力场精度相比GRACE计划有较大提升[28-29]。表2对地球重力卫星主要参数进行了对比。

图7 GRACE Follow-On卫星示意图Fig.7 Sketch of GRACE Follow-On satellite

2 卫星重力反演理论和方法研究现状

随着CHAMP、GRACE、GOCE、GRACE-FO的相继发射，目前已经积累了海量的地球重力场观测数据，如何高质量和高效率的处理这些观测数据以求得高精度和高空间分辨率的地球重力场模型成为国际上的研究热点。本节介绍了目前主流方法的研究进展，包括动力学法、能量守恒法和短弧积分法。

2.1 动力学法

动力学法是指利用地面GPS跟踪站观测数据、地面SLR观测数据、重力卫星仪器(星载GPS、加速度计、星间测距仪等)观测数据及其他相关数据联合解算GPS卫星和重力卫星轨道、地面跟踪站坐标、重力场参数以及其他相关动力学模型参数[30]。如式(1)所示：

(1)

动力学法虽然计算步骤复杂、累积误差较难控制，但是理论严密，求解精度较高。目前国际三大机构GFZ、JPL和CSR均采用动力学法反演高精度地球重力场模型。GFZ的Reigber等[31]基于动力学法，仅利用CHAMP卫星任务三个月的GPS卫星跟踪和加速度计数据恢复了地球卫星重力场模型EIGEN-1S，其在5°×5°格网下的大地水准面平均误差约为20 cm，相比之前利用传统卫星轨道观测数据恢复的地球重力场模型精度提升了2倍。CSR的Tapley等[32]也基于动力学法利用重力卫星数据恢复了GGM系列模型。

王长青等[33]基于动力学两步法利用GRACE Level 1B数据解算出IGG时变重力场模型，且模型精度与国际权威机构发布的时变重力场模型接近。罗志才等[34]为降低轨道共振现象影响，基于动力学积分法仅利用GRACE星间K波段距离变率(K-band range rate, K-BRR)恢复了60阶的时变重力场模型WHU-Grace01，对比结果表明与三大机构时变重力场模型具有较好的一致性。

Zhou等[35]在传统动力学法基础上提出了处理KBR残差低频噪声的过滤器预定策略(filter predetermined strategy, FPS)，将观测方程的观测向量和设计矩阵通过经验参数同时过滤，模拟实验表明FPS可以有效吸收KBR残差中的低频噪声。基于改进的动力学法利用13年的GRACE数据建立了HUST-Grace2016 s地球静态重力场模型，已接近主流地球重力场模型精度水平。

2.2 能量守恒法

能量守恒法依据具有普适性的能量守恒定律而建立，是获取地球重力场模型的重要途径之一[36]。能量守恒法基于卫星绕地球飞行时扣除所受非保守力后的动能、重力势能等总能量和为常数的特性，建立卫星动能与扰动位的关系[36]：

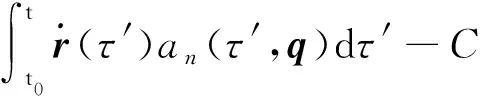
(2)

表2 地球重力卫星主要参数对比Table 2 Comparison of main parameters of Earth gravity satellite

自从O’Keefe[37]于1957年提出利用能量守恒法解算地球重力场模型以来，国际上对基于能量守恒法利用重力卫星观测数据反演地球重力场模型不断提出改进方法，但直到2003年德国慕尼黑工业大学才首次基于能量守恒法利用CHAMP重力卫星观测数据研制了TUM系列模型[38-39]。

郑伟等[40-43]对基于改进的能量守恒法恢复地球重力场模型进行了数值模拟研究，并解算了IGG-GRACE重力场模型；基于改进的能量守恒法对GRACE卫星的关键科学载荷精度与地球重力场模型精度的相关性进行了定量分析，给出了中国下一代重力卫星的关键科学载荷精度指标设计建议，并研究了地球重力场精度与GRACE卫星星体和SuperSTAR加速度计的质心调整精度的相关性。

2.3 短弧积分法

短弧积分法本质上由牛顿运动方程推导而来，将卫星轨道表示成Fredholm积分方程形式的边界值问题，然后用积分方程的方法求解地球重力场模型[44]。短弧积分法将弧段积分方程中任意历元的卫星状态向量表示为边界轨道参数、重力场待估参数和其他加速度参数的函数，进而解算地球重力场模型[45]。短弧积分法观测方程可表示为

(3)

(4)

德国波恩大学Ilk等[46]首先将利用短弧积分法基于卫星跟踪卫星数据恢复了重力场模型。Mayer-Gurr等[44]首次基于短弧积分法利用CHAMP卫星轨道数据恢复了ITG-CHAMP01模型(90阶)，后续又提出对几何轨道进行梯度改正后用于GRACE地球重力场反演。Schall等[47]基于短弧积分法利用7.5个月的GOCE重力梯度和轨道观测数据恢复了240阶的ITG-Goce02S模型，其精度与ESA同期发布的第二版GOCE地球重力场模型精度相当。

游为等[48]分析了短弧积分法中弧段长度和梯度改正对解算地球重力场模型精度的影响，得出30 min弧段长度且进行梯度改正最佳的结论。黄强等[49]分别对比了短弧积分法与能量守恒法在使用相同数据源情况下反演地球重力场模型的精度，结论显示短弧积分法的精度要高于能量守恒法。苏勇等[50]进一步对比了短弧积分法、能量守恒法和平均加速度法三种方法处理GOCE卫星数据的优劣性。

Chen等[51-52]对短弧积分法进行了改进，利用加权最小二乘法将所有轨道和距离速率改正与重力位系数和加速度计偏差联合求解，将传统的短弧积分法的弧段长度由1 h以内延展到2 h，并且不再需要边界位置参数；通过对加速度和卫星姿态数据的误差进行建模，减少了恢复的重力场模型的高频噪声。Chen等[51-52]基于改进的短弧积分法利用GRACE观测数据恢复了高精度的Tongji-GRACE系列模型及其时变模型。

3 地球重力场模型发展和现状

自2000年国际上第一颗重力卫星CHAMP发射以来，卫星重力反演理论与方法得到迅速的发展，各大机构均推出自己的基于卫星重力观测数据的地球重力场模型。国际地球模型中心(International Centre for Global Earth models, ICGEM)是国际大地测量学和地球物理学联合会(International Union of Geodesy and Geophysics, IUGG)所属的国际大地测量学协会(International Association of Geodesy, IAG)提供地球重力场模型上传与下载服务的权威中心，其收录了达到世界领先水平的地球重力场模型及其时变模型。目前国际上主流机构的卫星静态重力场模型如表3所示。

为分析基于单颗重力卫星反演地球重力场模型的精度，以EIGEN-6C4为参考模型，选取EIGEN系列CHAMP-Only模型、GGM系列GRACE-Only模型、GO_CONS_GCF_2_TIM系列GOCE-Only模型，分别进行精度评定。

图8所示为EIGEN系列CHAMP-Only模型的大地水准面高和大地水准面累积误差，表4列举了部分CHAMP-Only模型大地水准面累积误差统计。结果表明，随着CHAMP观测数据的增加，在70阶以内EIGEN-CHAMP05S模型与EIGEN-6C4模型符合较好，精度明显优于其他模型，70阶以后EIGEN-1、EIGEN-2、EIGEN-CHAMP03S、EIGEN-CHAMP05S模型精度均较差。因此，CHAMP卫星观测数据更适合反演70阶以内地球重力场模型，适当增加CHAMP观测数据长度有利于提高中长波部分的地球重力场模型精度。

表3 卫星重力模型对比Table 3 Comparison among earth’s satellite gravitational field models

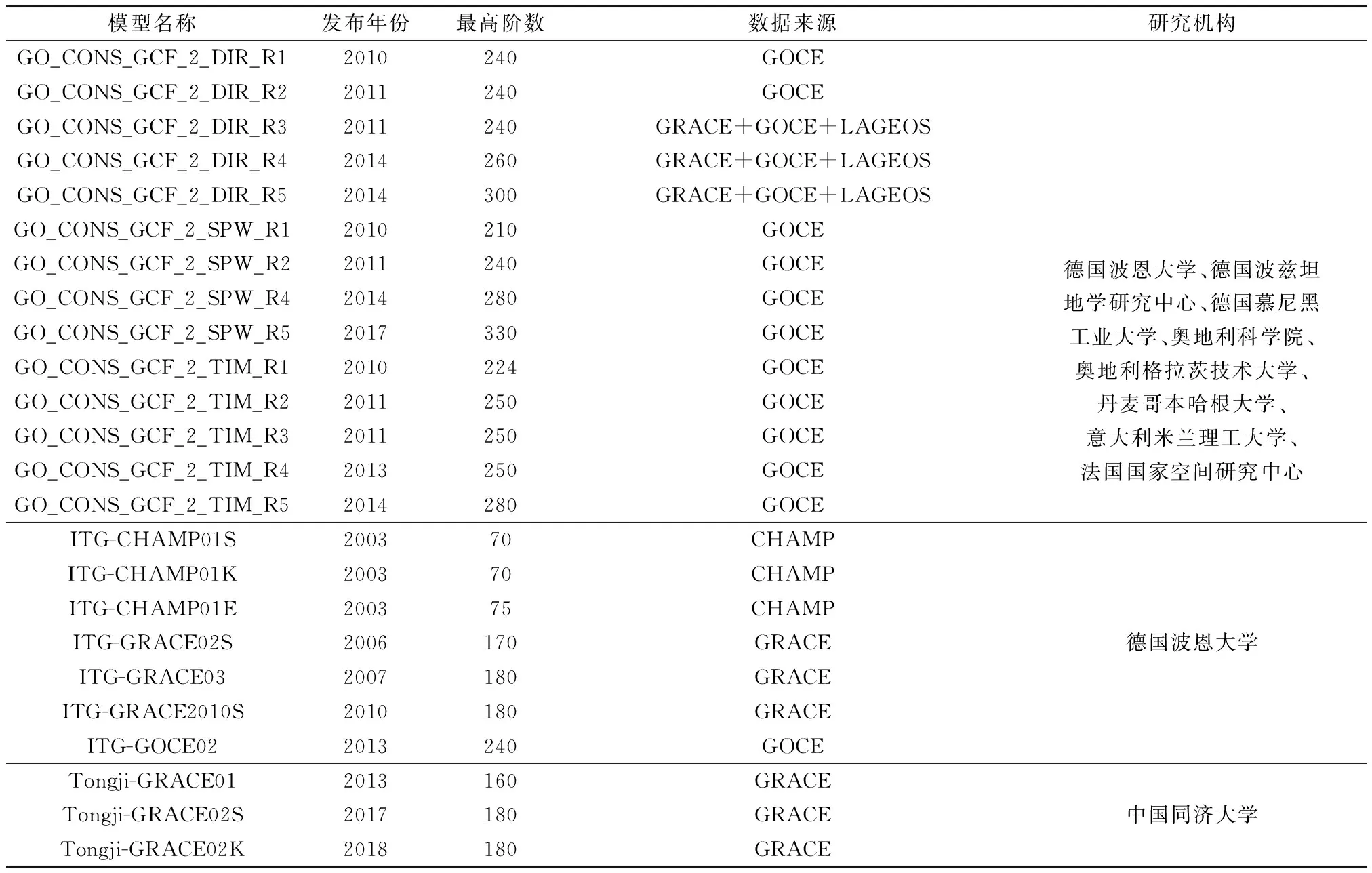
续表3

图8 CHAMP-Only系列模型大地水准面高及大地水准面累积误差对比Fig.8 Comparison of geoid height and cumulative geoid height error from CHAMP-Only models

图9为GGM系列GRACE-Only模型大地水准面高和大地水准面累积误差，表5列举了部分GRACE-Only模型大地水准面累积误差统计结果。结果表明，在观测数据足够的情况下，直到150阶GGM-05S模型与EIGEN-6C4的符合程度均较好，150～180阶GGM03S和GGM05S的大地水准面累积误差均增大10倍。因此，GRACE观测数据更适合反演150阶以内的地球重力场模型，适当增加GRACE观测数据时间长度有利于提高短波部分的地球重力场模型精度。

图10为GO_CONS_GCF_2_TIM系列GOCE-Only模型的大地水准面高和大地水准面累积误差，表6列举了部分GOCE-Only模型大地水准面累积误差统计结果。结果表明，在一定范围内GO_CONS_GCF_2_TIM系列地球重力场的反演精度与观测序列长度正相关，其中GO_CONS_GCF_2_TIM_R5在前220阶与EIGEN-6C4符合程度都非常高，但在220阶之后提升有限。GOCE卫星观测数据相对于GRACE和CHAMP，对地球重力场高频信号更敏感，适合反演地球重力场短波部分。

图9 GRACE-Only系列模型大地水准面高及大地水准面累积误差对比Fig.9 Comparison of geoid height and cumulative geoid errors from GRACE-Only models

图10 GOCE-Only系列模型大地水准面高及大地水准面累积误差对比Fig.10 Comparison of geoid height and cumulative geoid errors from GOCE-Only models

表4 CHAMP-Only模型大地水准面累积误差统计Table 4 Statistics of cumulative geoid height error from CHAMP-Only models

表5 GRACE-Only模型大地水准面累积误差统计Table 5 Statistics of cumulative geoid height error from GRACE-Only models

表6 GOCE-Only模型大地水准面累积误差统计Table 6 Statistics of cumulative geoid height error from GOCE-Only models

从上述分析中可看出，单独利用CHAMP、GRACE或GOCE重力卫星观测数据反演地球重力场都存在一定缺陷。各个重力卫星受其观测模式和轨道高度的影响，对不同阶数的地球重力场敏感程度不同，且一定范围后单纯增加观测数据长度对提高地球重力场模型精度提升有限。因此，融合CHAMP、GRACE和GOCE重力卫星观测数据是提高地球重力场模型精度的重要途径。

4 地球时变重力场模型的应用研究进展

自2002年第一颗重力卫星CHAMP升空到至今，国际上发表了很多有关地球重力卫星应用的研究成果。据统计，目前在《Nature》《Science》及其主要子刊《Nature Geoscience》《Nature Communications》和《Science Advances》有关地球重力卫星的论文多达28篇。其中，《Nature》4篇，《Science》12篇，《Nature Geoscience》9篇，《Nature Communications》2篇，《Science Advances》1篇。各应用领域发表篇数如图11所示，可以看出国际上地球时变重力场模型的应用研究主要聚焦于冰川冰盖与海平面研究，原因是重力卫星可以较为准确的监测冰川冰盖以及区域海洋质量变化。

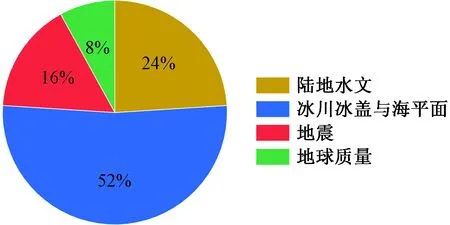
图11 《Nature》和《Science》刊登卫星重力论文的应用领域分析Fig.11 Analysis of the application fields of satellite gravity papers published in “Nature” and “Science”

地球时变重力场模型的应用是研究地球重力场的关键目的，国际上主要通过GFZ、CSR和JPL发布的GRACE时变重力场模型来研究地球卫星重力场的应用。GRACE重力卫星结束使命后，CSR、GFZ和JPL重新处理了完整的15年的GRACE任务数据，发布了各自最新的RL06地球时变重力场模型，基于GRACE卫星时变重力场模型的应用研究仍有较大进步空间。下一步将基于GRACE-FO任务开始新一轮地球时变重力场模型及其应用的研究。综述了基于GRACE卫星时变重力场的主要应用研究方向，包括陆地水文研究、冰川冰盖与海平面研究和地震研究。

4.1 陆地水文研究进展

GRACE任务最重要的贡献之一就是揭示了全球陆地水文变化趋势，即地球总体上呈现高纬度和低纬度地区水储量增加，中纬度地区水储量减少的趋势，这对淡水资源利用、食物安全保障等具有深远的影响[2]。

Rodell等[3]研究了近年来全球可用淡水资源的新趋势，利用2002—2016年间共14年的GRACE重力卫星观测数据量化了34个陆地区域淡水资源存储趋势，并将这些趋势驱动因素分类为自然年度变化、不可持续的地下水消耗(即人类影响)、气候变化或上述因素的组合。研究表明，最大的淡水资源损失发生在南极洲、格陵兰岛、阿拉斯加湾海岸和加拿大群岛四个区域，这些区域的冰川和冰盖消融极可能是受到全球气候变暖的影响，在北美洲、欧亚大陆和热带地区淡水资源总体上增加，但是在中国华北、印度北部、中东地区和美国南部地区淡水资源正在枯竭，文中推测是人类活动的影响。Rodell等[3]的研究揭示了在人口密集区域淡水资源将会更加珍贵，同时由于气候变化影响，全球冰盖和冰川消融现象将继续加剧。

Reager等[4]通过GRACE观测数据量化河流流域的水储量，并通过河流流域水储量估算流域洪水潜力，最终提供洪水预警。当一个区域的水储量增加时，该区域的重力信号也会按比例增加，GRACE卫星正是通过这个原理监测大型区域的水储量变化，由GRACE任务反演的地球时变重力场模型可监测大于200 000 km2的总蓄水量变化。Reager等使用2011年密苏里河洪水作为案例进行研究，建立了由水文监测站测量的河流流量与由GRACE任务测量的河流流域范围内的水储量之间的关系。通过应用时间滞后的河流流量自回归模型，可利用基于GRACE任务的水储量信息提前5～11个月评估河流流域发生洪水的可能性，为河流流域提供洪水预警。

4.2 冰川冰盖与海平面研究进展

随着过去的几十年里全球气候变暖情况不断加剧，地球上几乎所有冰川冰盖的质量损失率急剧上升，由此导致了全球平均海平面上升一半以上。通过GRACE卫星监测地球区域重力异常变化，可以研究长时序的全球冰川冰盖的质量变化以及全球海平面的升降情况，为分析全球气候变暖带来的冰川冰盖与海平面的影响提供可靠的数据支撑。

Farinotti等[5]利用GRACE卫星重力测量、卫星激光测高和冰川模拟3种方案对比研究了天山山脉冰川近50年的变化情况，并综合结果分析了天山山脉的冰川消退的原因。中亚的人口严重依赖天山山脉的雪和冰川融化供水，研究天山山脉冰川消退情况及其驱动因素具有重要意义。Farinotti等使用基于卫星重力测量、激光测高和冰川模拟的3个独立方案来估计天山的总冰川质量变化，这三种方案的研究结果一致：1961—2012年，天山山脉冰川总面积和总质量分别减少18.6%、27.15%，分析结果表明，天山山脉冰川总面积和质量下降的主要原因是夏季融化过快，这可能与北大西洋和北太平洋的气候变暖与环流变化的综合影响有关。

Forsberg等[6]利用13年的GRACE观测数据研究了格陵兰岛和南极洲的质量变化及其对全球海平面的影响。由GRACE卫星任务得到地球的时变重力场模型分析格陵兰岛和南极洲的质量变化，发现在2002—2015年期间格陵兰岛质量损失达(265±25) GT/年(包括外围冰帽)，南极洲质量损失达(95±50) GT/年，相当于全球平均海平面分别升高0.72、0.26 mm/年。在2002—2015年，南极洲的质量损失显著加速，格陵兰岛的质量损失在持续加速，但在2012年达到创纪录的峰值后，格陵兰岛质量损失趋势相对略有下降。Forsberg等联合GRACE和卫星测高确定了格陵兰岛和南极洲质量变化的来源：格陵兰岛的质量变化与边缘冰区有关，特别是在格陵兰岛西部和东南部以及Jakobshavn和Helheim等主要的溢出冰川最为明显；南极洲的质量变化与西南极洲(主要是松岛和思韦茨冰川系统)以及南极半岛的主要溢出冰川有关。

4.3 地震研究进展

地震导致区域地壳形变的同时也会引起区域重力异常变化。利用GRACE卫星可监测到特大地震(一般为8级以上)引起的重力异常变化，也可捕捉到地震前板块运动引起的重力异常变化。因此，GRACE地球时变重力场模型在地震研究中具有广阔的应用前景。

Panet等[7]利用GRACE观测数据分析了2011年3月日本东北大地震周围广阔时空范围内的地球重力场变化，揭示了地震前的板块变形模式。基于GRACE任务的地球时变重力场模型显示，地震周围区域的重力变化开始于在地震前几个月，且震中附近的地震信号被整个板块俯冲系统的大尺度变化所包围。从2010年末开始，地震区域重力变化在震中两侧发展。在2011年3月，重力变化沿着地震区域三个构造板块的俯冲边界扩散。地震之后，重力变化逐渐集中在震中附近。Panet等[7]的研究结果表明，在地震发生之前，板块侵入上地幔的时间尺度达几个月，因此利用地球时变重力场模型可以提前几个月监测到这种大地震前兆信号，这可以用于地震灾害预测。

5 钱学森空间技术实验室天空海一体化导航与探测团队研究进展

钱学森空间技术实验室天空海一体化导航与探测团队在卫星重力反演和卫星重力水文应用方面已经取得阶段性研究成果。本节综述了天空海一体化导航与探测团队在地球重力场模型建立、下一代卫星重力计划和卫星重力水文应用方面的研究进展。

5.1 卫星重力反演

5.1.1 地球重力场模型建立

郑伟等[41]详细阐述了GRACE重力卫星关键载荷仪器实测数据的处理过程，并基于能量守恒法利用6个月的GRACE Level 1B实测数据解算了120阶的IGG-GRACE地球重力场模型。首先对6个月的GRACE卫星 Level 1B实测数据进行轨道拼接、粗差探测、线性内插、重新标定、坐标转换、误差分析等有效处理，然后基于无参考扰动位的能量观测方程利用有效处理后的GRACE数据建立了120阶的IGG-GRACE地球重力场模型。对比同期的EIGEN-GRACE02S，由于采用了更长时序的GRACE观测数据，IGG-GRACE在低频部分精度略高于EIGEN-GRACE02S；由于采用的GPS观测数据采样率仅为EIGEN-GRACE02S的1/6，IGG-GRACE在高频部分精度略低于EIGEN-GRACE02S。

郑伟等[53]利用12个月的GRACE实测数据基于星间距离插值法(inter-satellite range interpolation method, IRIM)解算了120阶的WHIGG-GEGM01S地球重力场模型。通过将精确的星间距离引入相对轨道位置矢量的视线(line-of-sight, LOS)分量，利用卫星轨道位置、星间距离和非保守力首次建立了星间距离插值方程。通过多点星间距离插值方程解算对比，确定9点星间距离插值公式能有效提高恢复地球重力场的准确性。相对于其他方法，星间距离插值法具有形式简单、物理意义明确、对地球引力场变化敏感、计算要求低等优势。WHIGG-GEGM01S地球重力场模型在120阶处累积大地水准面高度为1.098×10-1m，重力异常误差为1.741×10-6m/s2，与同期EIGIN系列地球重力场模型精度处于同一水平。

郑伟等通过将精确的星间距离速率测量值引入到轨道速度差矢量的视线分量中，建立了基于星间速度牛顿插值法(intersatellite range-rate interpolation approach, IRRIA)的卫星观测方程，并解算了120阶的WHIGG-GEGM02S地球重力场模型[54]。通过对比2点、4点、6点和8点星间速度牛顿插值公式，验证了使用6点星间速度牛顿插值公式可以显著提升地球重力场模型反演精度。WHIGG-GEGM02S在120阶处的累积大地水准面高度误差为1.140×10-1m，累积重力异常误差分别为1.807×10-6m/s2。通过与现有GRACE地球重力场模型进行全球定位系统/水准观测误差对比，WHIGG-GRACE02精度与同期的GGM02S精度接近。

郑伟等[55]通过将高精度K波段星间测距(KBR)观测值引入双星动能差中，建立了基于新型能量插值法的卫星观测方程，并恢复了120阶的WHIGG-GEGM03S地球重力场模型。分别验证了2点、4点、6点和8点能量插值观测方程对地球重力场反演精度的影响，研究结果表明基于6点能量插值观测方程有利于提高地球重力场的反演精度。利用美国、欧洲和澳大利亚的全球定位系统/水准观测数据检验了WGIGG-GEGM03S地球重力场模型，并对EIGEN系列模型进行了精度对比，结果表明，WHIGG-GEGM03S接近现有的EIGEN-GRACE02S模型。

5.1.2 下一代卫星重力计划

天空海一体化导航与探测团队立足于当前重力卫星任务，展望下一代卫星重力计划，目前已经取得一系列研究成果。

郑伟等[56-58]基于改进的半解析法模拟研究了不同轨道高度与星间距离对利用下一代重力卫星Improved-GRACE反演的地球重力场模型精度的影响，综合考虑卫星寿命和累积大地水准面精度，认为较优的Improved-GRACE重力卫星设计平均轨道高度为350 km，平均星间距离为50 km；综合考虑卫星轨道高度、轨道倾角、星间距离对地球重力场模型精度的影响，通过设置不同卫星轨道参数分别反演了120阶地球重力场模型，通过模型精度对比研究并考虑卫星寿命，最终提出了Improved-GRACE卫星重力计划的优化轨道参数：卫星轨道高度(300±50)km，轨道倾角89°±2°，星间距离(50±10) km；从卫星设计制造、卫星跟踪模式、卫星轨道参数、仿真模拟在CSGM中的应用和反演方法各个方面研究论证了中国卫星重力任务(China’s satellite gravity mission, CSGM)，并提出了将来CSGM重力卫星任务的科学目标：在300阶处累计大地水准面精度达到1～5 cm，累积重力异常精度达到1～5 mGal。

郑伟等[59-61]分别研究了联合串行式和钟摆式卫星编队、三向车轮双星编队和四星转轮式编队三种卫星编队方式对地球重力场模型精度和空间分辨率的影响，研究表明，改进卫星编队方式对提高地球卫星重力场模型时空分辨率和精度有较大帮助。

5.2 卫星重力水文应用

钱学森空间技术实验室天空海一体化导航与探测团队的尹文杰等基于GRACE地球时变地球重力场模型和其他水文模型，在卫星重力水文应用方面取得了阶段性成果。

尹文杰[62]等结合GRACE数据、全球降水气候计划(global precipitation climatology project, GPCP)数据和全球陆面同化系统(global land data assimilation system, GLDAS)数据，分别计算陆地水储量变化、土壤水含量变化、雪水当量变化和降水量变化，最后反演确定甘肃北山地区2003—2012年的地下水储量每年约下降0.26 cm。随后，利用GRACE数据和其他水文模型数据，尹文杰等[63]对比分析了1980—2015年甘肃北山地区地下水储量变化趋势，研究发现甘肃北山地区地下水储量总体上呈下降趋势。

尹文杰[64]基于GRACE时变重力场模型获取陆地水储量信息，在利用GLDAS模型扣除土壤水分和雪水后，确定了中国北方地区的地下水储量变化，并和中国官方公布的地下水监测数据进行了对比，分析地下水储量变化的原因。研究结果表明，2003—2012年华北地区地下水年平均耗竭率为0.17 cm/y，华北地区地下水储量普遍呈下降趋势，京津冀地区地下水资源面临枯竭，推测原因主要是地下水超采。由于GRACE任务空间分辨率限制，尹文杰等[65]提出了利用蒸散(evapotranspiration, ET)模型数据提高GRACE反演地下水储量异常空间分辨率的降尺度方法。通过降尺度方法，华北平原地下水储量异常空间分辨率从110 km降至2 km，且与地下水观测井数据一致。

6 地球卫星重力场模型未来展望

2000年以来，随着地球重力卫星的相继发射，利用重力卫星获取数据并解算地球重力场模型的理论与方法迅速发展，地球重力场模型的精度和分辨率均得到较大提升。虽然目前已经反演出超高阶(2 190)地球重力场，但仍不能满足当前各个领域的应用需要按目前发展趋势，要进一步提升地球重力场模型精度和分辨率，可从以下几方面发展。

6.1 改进卫星重力反演方法

目前国际上获取高精度和高分辨率地球重力场模型主要依靠动力学法，但动力学法本质上是数值积分，存在长弧段轨道误差难以修正、计算难度较大等缺点。未来在长弧段轨道误差控制、非保守力改正模型的精化、高效并行计算等方面需要加快研究。同时，2005年以来迅速发展的短弧积分法在高精度和高分辨率地球重力场反演上产生了较大作用，利用短弧积分法解算的地球重力场模型精度和分辨率甚至优于同期的部分动力学法产品，未来短弧积分法将大有可为。

6.2 参考力模型的精化

无论使用何种卫星重力反演方法，参考背景力模型都是得到高精度和高分辨率地球重力场模型不可或缺的部分。参考力背景模型主要包括N体扰动模型、地球固体潮汐和地球固体极潮模型、大气与海洋潮汐模型、海洋极潮广义相对论扰动模型和非保守力模型，对上述参考力模型进行改进优化是提升地球重力场模型精度和分辨率的重要手段。

6.3 多源重力观测数据融合研究

前人研究已经证明，融合多源重力观测数据对提升地球重力场模型整体精度有较大帮助。CHAMP、GRACE、GOCE和GRACE-FO为地球重力反演提供了海量的卫星重力观测数据，同时还有海洋测高数据和地面/航空重力观测数据。如何完美融合上述数据是未来研究的关键问题。目前发布的超高阶地球重力场模型均为融合多源重力观测数据后得到的产品。因此，多源重力观测数据融合研究将是未来研究的热点。

6.4 下一代重力卫星任务

2018年发射的GRACE-FO仅是GRACE任务的延续，除搭载实验性质的激光干涉测距仪外与GRACE基本没有不同，并不是国际上普遍认为的下一代重力卫星。研发轨道高度300 km以下、搭载非保守力补偿系统且全面升级科学仪器的下一代重力卫星对反演高精度和高空间分辨率地球重力场模型具有本质性提升。

7 结论

随着地球重力卫星CHAMP、GRACE、GOCE和GRACE-FO的相继发射，地球卫星重力场模型的构建及应用在近20年来飞速发展。单一重力卫星的数据反演地球重力场模型空间分辨率和精度均有限，融合多源数据(包括重力卫星、海洋测高和地面监测站数据)有利于提高地球重力场模型的空间分辨率和精度。最新融合多源数据的超高阶地球重力场模型EIGEN-6C4已达到2 190阶且精度超过EGM2008。地球卫星时变重力场模型在陆地水文、冰川冰盖与海平面和地震分析等方面的应用具有重要意义，有助于提高人们对全球气候变化、地震预警的认识。钱学森空间技术实验室天空海一体化导航与探测研究团队在地球重力场模型建立、下一代地球重力卫星计划和卫星重力水文应用上已经取得一定成果。同时，团队正在开展基于GNSSR卫星海面测高原理反演高精度海洋重力场，用以提高水下惯性/重力组合导航精度的研究，并取得了阶段性研究成果[66-68]。