基于局部结构的涡轮导向器屈曲故障模式分析

张 帆，冯引利，高金海，郭宝亭，蒋文婷

(1.中国科学院工程热物理研究所轻型动力重点实验室，北京 100190；2.中国科学院大学，北京 100049)

1 引言

结构屈曲是机械、航空航天、核能等领域普遍发生的故障现象，受到众多研究人员的重视。早在1961年Timoshenko[1]就对经典屈曲理论进行了较为全面的完善总结。针对各类简单板壳结构，Gellatly[2]研究了夹层圆筒的屈曲并求出了临界温度；Whitney 等[3]运用能量法确定了复合材料层合板的临界温度；丁红丽[4]基于广义变分原理得出了衬壳弹性屈曲问题的控制方程与边界条件；Wu等[5]基于Donnell圆筒壳稳定性方程研究了其热弹性稳定性。对于航空发动机部件等复杂结构，高金海等[6]提出了局部屈曲的理论计算模型并应用于燃烧室屈曲的求解；邓可顺[7]给出了复杂结构屈曲的有限元方程及其解法；吴长波等[8]针对喷管隔热罩和涡流器的失稳问题做了分析优化；雷友峰等[9]则针对燃烧室蠕变屈曲现场做了理论分析。在试验研究方面，NASA[10-11]曾在1991 年和2004 年进行过热机械载荷下航天飞机壁板的屈曲特性试验；Kicher 等[12]进行了钢衬圆柱壳的屈曲试验。

在航空发动机常规静子件强度校核中，往往重点关注结构静强度、振动和寿命问题，而忽视薄壁件的热稳定性问题。国内外学者针对燃烧室机匣的屈曲问题开展过一些研究[6]，但针对涡轮部件在复杂温度场作用下发生屈曲的问题尚未见报道。

在复杂结构屈曲分析中，往往由于模型过大导致网格划分不够精密，轻则影响计算效率，重则得到错误的应力峰值，因此复杂结构的屈曲计算及结构优化往往耗费大量时间且优化结果不理想。传统的屈曲判别与优化方法已难以满足复杂结构设计需要，亟须提出一种快捷、准确的优化方法。

某型涡扇发动机试车后发现低压涡轮二级导向器内环发生了波瓣形变形，本文对试验过程中发生的失效模式进行了分析，提出一种基于子模型的复杂结构屈曲计算方法，可大大简化计算流程，提高热结构的分析设计水平。

2 结构应力分析与屈曲计算方法

首先分析结构应力分布，进而提出一种基于子模型的复杂结构屈曲计算方法，通过将整体结构的应力分布等效为子模型的边界压应力，计算子模型的屈曲失效。

2.1 导向器结构应力分析

该型涡扇发动机试车后低压涡轮二级导向器内环发生的波瓣形变形如图1(a)所示，发动机运行过程中导向器结构的真实边界如图1(b)所示。A 点处外机匣与导向器外环直接接触，并对其产生一定压力。根据极限条件计算该处压力为120 MPa。此外，外机匣对A 点导向器外环有周向限位。B 点处外机匣与导向器外环初始设计为间隙配合，但在极限条件下会产生接触，因此在B 点对导向器外环设置轴向和径向约束。

图1 涡轮导向器波瓣形失效Fig.1 Lobe failure of turbine nozzle

导向器结构除了受外机匣作用力外，还受到因内外涵道气流温差引起的沿径向分布的热载荷。其中，导向器内环封严唇处在极限条件下最大温度达712℃，整个导向器结构最大温差达500℃。由于防止气流倒灌的封严唇设计(图1(b)中红色圈内)，使得导向器内环封严唇处成为悬臂结构，易出现破坏、屈曲等问题。

为校核试验后出现的变形，首先计算导向器结构在热载荷和机械载荷作用下的应力分布。导向器结构材料为铸造高温合金K403。考虑材料参数受温度变化影响，材料性能如表1所示。使用Solid185三维8节点固体结构单元对导向器结构进行网格划分，共得到3 725 972个单元。施加CFD计算得出的温度场与气动载荷，计算该边界条件下的静应力。最大等效应力与第三主应力的计算结果如图2所示，可以看出最大等效应力集中在内环轮缘封严处，且主要表现为周向压应力。最大等效应力达屈服强度的2倍，需重点考核该部位的稳定性。

2.2 子模型屈曲计算方法

对于同时受到热载荷和机械载荷的局部结构，可将其等效为图3 所示的四边受压应力作用，面内受热载荷，边长为a、b，厚度为h的固支板。根据该板的控制方程和边界条件，可推导该子模型的临界温度和临界压应力。

表1 K403的材料属性Table 1 Material properties of K403

图2 导向器结构应力分布Fig.2 Stress distribution of turbine nozzle

图3 考虑热载荷与机械载荷的固支板Fig.3 Fixed plate considering thermal load and mechanical load

固支板四边挠度均为0，则壳体薄膜内力可以表示为：

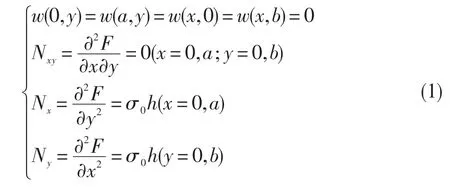
受热板的无量纲控制方程为：

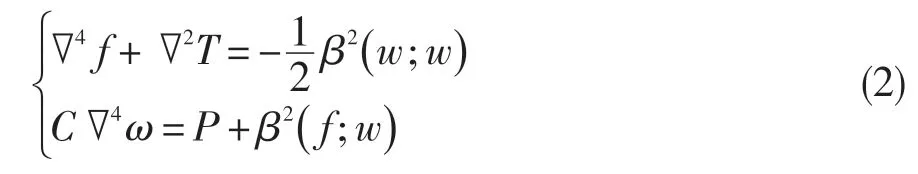
式中：f为应力函数，T为温度函数，w为位移函数，P表示机械载荷(主要表现为压力)，β为固支板长宽比，(;)=。

对于承受热载荷和机械载荷(主要为压应力，由其他非热载荷引起)的固支板，采用初始后屈曲渐进分析理论对非线性控制方程进行求解，可得到含有热载荷项和机械(或气动)载荷项的特征值方程式[13]，进而得到局部结构的临界压应力为：

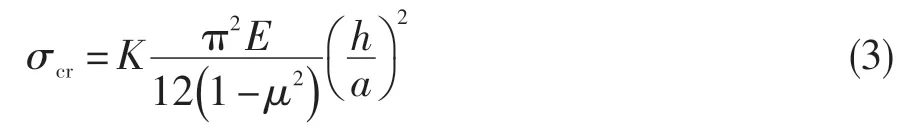
式中：K为β的函数。

根据前文应力分析结果，导向器内环封严唇存在压应力集中，可将其近似为薄壁圆筒，如图4 所示。由于该局部结构仅一侧截面存在外部等效边界条件，故可以提取左侧与整体结构连接处的位移边界条件和圆筒壁面的压应力。若将其近似等效为悬臂圆筒，即左侧挠度为零，则其屈曲临界压力可表示为：

图4 导向器局部结构示意图Fig.4 Local structure diagram of turbine nozzle

式中：δ为圆筒厚度，R为圆筒半径，L为圆筒长度，c为圆筒屈曲波数。

由悬臂圆筒受压屈曲理论公式可以看出，除边界条件外，影响圆筒屈曲的重要因素包括圆筒的半径、厚度和长度。

3 局部屈曲求解与结构优化

3.1 屈曲有限元计算方法

子模型计算屈曲的重点在于如何准确提取局部结构的边界条件，而借助有限元软件可简易、快速提取。机械载荷与热载荷同时作用下的节点力可表示为：

同时，几何刚度矩阵由两部分构成：

式中：[Kg,P]、[Kg,T]分别为与载荷和温度场有关的刚度矩阵。

据此可将稳定性方程写为：

现有大型有限元计算软件可以实现局部结构边界条件提取，从而对局部结构进行特征值屈曲计算。首先计算全尺寸模型下的应力分布结果，提取压应力最大处的局部结构，并将局部结构外部应力或边界的影响作为边界条件提取，最后计算局部结构的特征值屈曲。在有限元软件中提取局部结构求解的具体步骤如图5所示。

提取导向器的内环封严唇结构，然后分别对提取结构和整体结构进行特征值屈曲求解，得到的屈曲波形如图6 所示，屈曲安全系数为1.25。屈曲波形与试验结果完全一致，均体现为内环轮缘封严处的波瓣形屈曲，证明该结构确实存在极大屈曲风险。

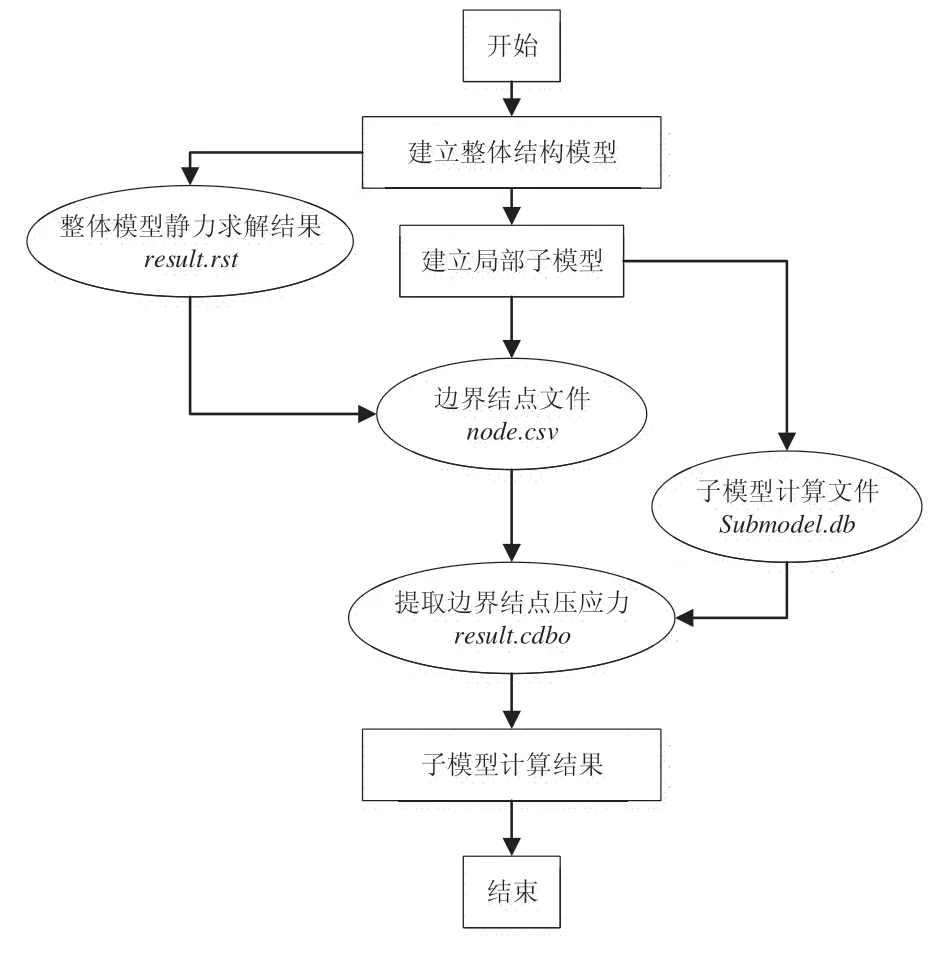
图5 局部结构在有限元程序中的计算步骤Fig.5 Calculation steps of local structure in finite element program

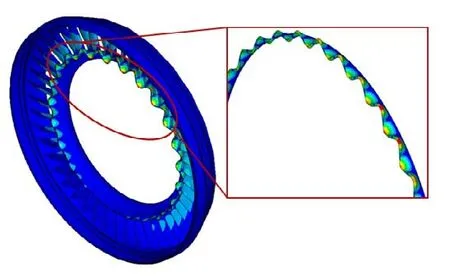
图6 局部屈曲计算Fig.6 Local buckling calculation

受压情况下构件的弹性屈曲被认为已经破坏，屈曲安全系数是判断结构件稳定性是否满足条件的重要参数，其表达式为：

式中：Pk为临界载荷，Pmax为飞行包线内机匣可能发生的最大工作载荷。

根据航空发动机结构设计准则[14]，对于民用发动机，要求发动机机匣的屈曲安全系数大于2.0。

综上看出，防屈曲设计可从改变载荷环境、改变边界条件和优化结构几何外形三个方面实现。若在不改变该结构的条件下对温度场进行优化，可以通过空气系统的设计降低整体结构的温度梯度，但此类做法需对发动机结构进行较大变动。优化导向器结构几何尺寸和在质量允许范围内强化结构则成为优化方向。

3.2 导向器局部结构的优化

结合薄壁圆筒的理论解和有限元计算公式，可将局部结构屈曲安全系数描述为：

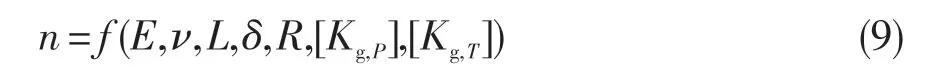
式中：E、ν分别为材料的弹性模量和泊松比。

在不改变载荷和边界条件的情况下，要提高薄壁圆筒件的稳定性，只能通过增加圆筒壁厚度的方法。对比两种增加厚度的方法，即封严唇整体加厚或部分加厚(图7方案1与方案2)。极限状态下整体加厚后的屈曲安全系数见表2，可见整体加厚之后屈曲安全系数可以满足设计准则要求。但屈曲波形没有发生变化，且系数裕度较低，仍存在一定屈曲风险。

图7 局部加厚与整体加厚方法Fig.7 The method of local thickening and integral thickening

表2 整体加厚后的屈曲安全系数Table 2 Buckling safety factor after integral thickening

若考虑局部加厚，即在内环内壁面添加环形加强肋，热应力大幅下降，屈曲安全系数增加到12.21，且屈曲波形发生改变，一阶屈曲波形表现为节径型，很好地解决了此类失效问题。故最终选择在内环内表面添加环形加强肋。

3.3 针对边界条件的优化

根据极限状态点应力计算结果，A 点径向压力与B 点约束边界条件均对热应力产生了较大影响，下面通过有限元计算研究此两个边界变化量对屈曲安全系数的影响。为此，设置如表3所示的7个不同边界条件计算组。其中，1～4组计算研究A点处外机匣对导向器产生的径向压力对结构屈曲的影响，4～7组计算研究B点处导向器外环因热膨胀造成的径向位移对结构屈曲的影响。

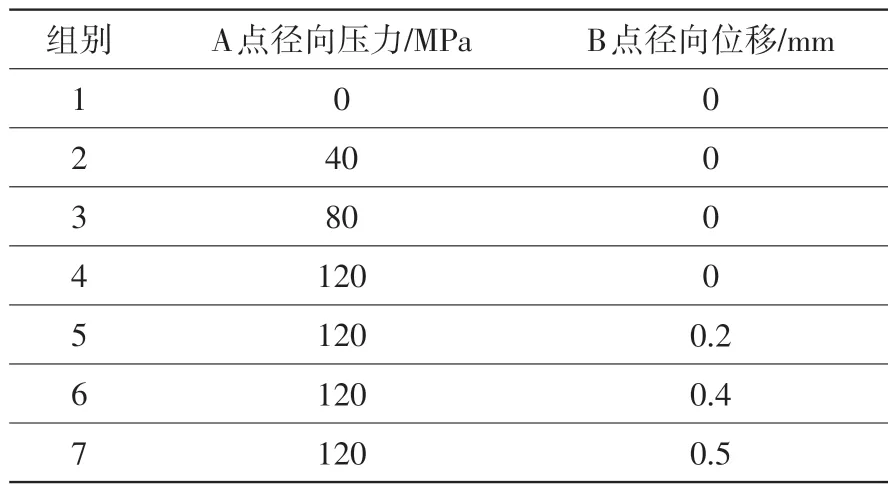
表3 边界条件计算组Table 3 Boundary condition calculation group

首先考虑A 点压力约束对屈曲安全系数的影响。根据1～4 组条件计算的屈曲安全系数随A 点径向压力的变化关系如图8(a)所示，可见随着径向压力的减小屈曲安全系数大幅增加，因此A 点边界可以作为优化目标。其次考虑B点位移约束对屈曲安全系数的影响。根据4～7 组条件计算的屈曲安全系数随B 点径向位移的变化关系如图8(b)所示，可见屈曲安全系数随着径向位移的增加而增大，但其增度低于A 点压力减小时的增度。据此，仅选择A点作为优化对象。将与A点接触的外机匣改为齿形结构，如图9所示。

根据本节分析结果可以看出，除在导向器内环内壁面增加加强筋外，改变与A点接触外机匣结构，将外环与外机匣连接处改为齿形结构，使其不对A点产生径向压力，可以很好地解决此种屈曲失效问题。在后续的发动机试车中未再出现此故障，验证了优化方向的正确性。

4 结论

针对航空发动机试车后发现的导向器屈曲现象开展了相关研究，主要得到下列结论：

(1)试车后出现的导向器内环波瓣形失效，为热载荷与机械载荷联合作用的热屈曲问题。

(2)除边界条件外，影响悬臂圆筒屈曲的重要因素还包括圆筒的半径、厚度和长度。

(3)借助有限元软件可简易快速地提取局部结构的边界条件，以屈曲安全系数为优化目标得到的导向器内环壁面增加加强筋和改变A点接触外机匣边界的优化结构，均可以很好地解决屈曲失效问题。

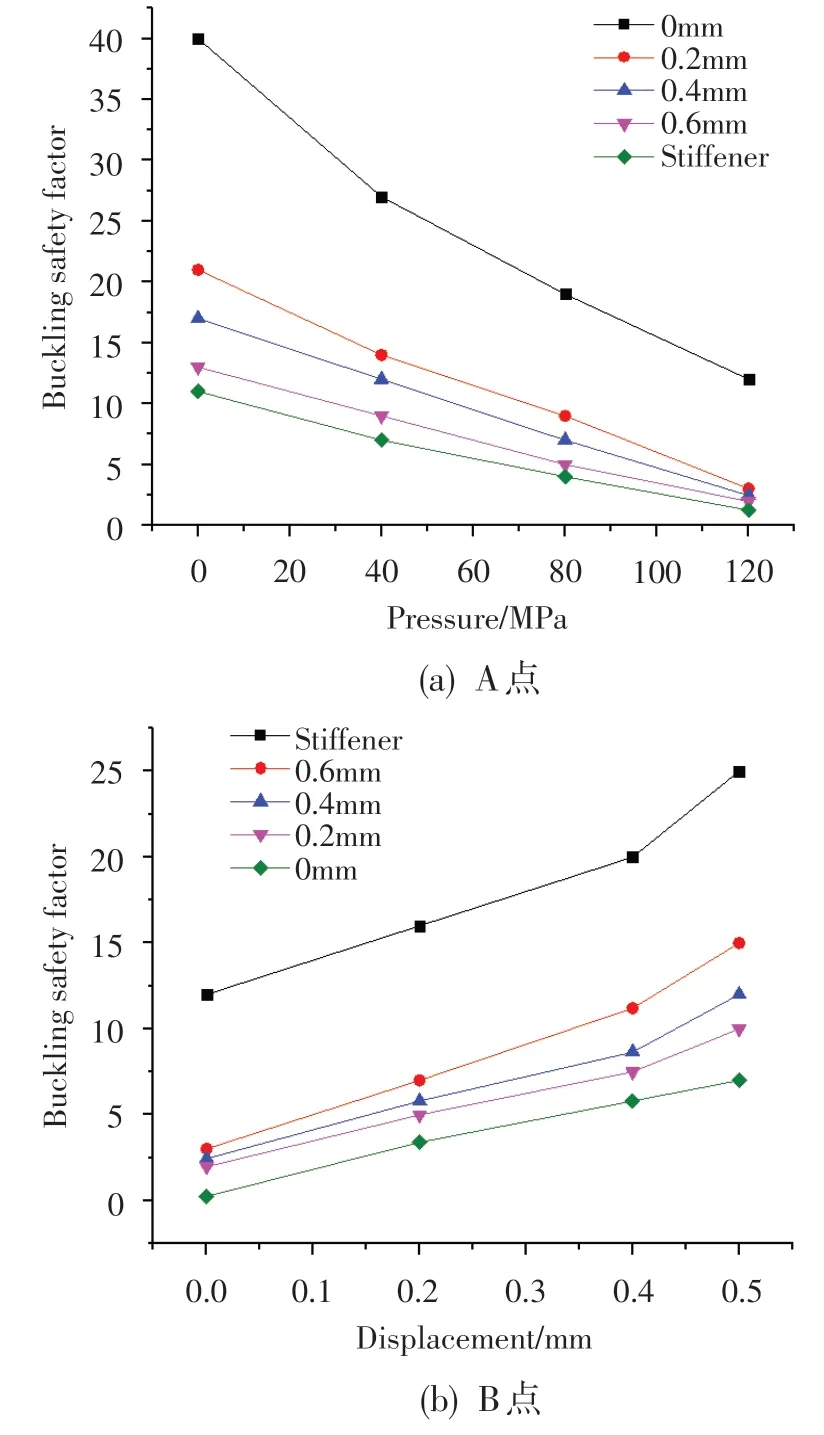
图8 屈曲安全系数随A点径向压力和原有B点径向位移的变化关系Fig.8 Variation of buckling safety factor with radial pressure of A point and radial displacement of B point

图9 导向器齿形结构Fig.9 Tooth structure of turbine nozzle