一种复合材料层合板孔边单层应力计算方法

(中国航发四川燃气涡轮研究院，成都 610500)

1 引言

复合材料层合板是一种重要的工程结构材料，具有比强度高及可设计的优点，在航空航天领域应用广泛。在复合材料层合板构件中，往往会存在结构性或功能性开孔特征，而开孔导致的应力集中使得孔边成为结构的薄弱位置，因此复合材料层合板孔边应力及强度分析是工程设计的重要内容之一。

复合材料层合板是一种典型的非均质各向异性材料，其开孔边应力与均质各向同性材料的有明显区别，但也具有一定的相关性，迄今已有众多学者对此做了大量研究。Wu 等[1]采用各向同性含孔板分析中应力集中因子的概念进行复合材料层合板开孔边应力分析，并提出一个计算正交各向异性含孔板和含孔圆柱壳应力集中因子的经验公式。吴德隆[2]采用保角映射方法，针对板类复合材料开孔问题建立的一般化分析理论，可对任意形状和孔角半径的孔进行分析，确定孔边及其附近的应力和应变分布，进行开孔补强分析和设计。韩小平等[3]将复合材料层合板简化为各向异性板，再利用含孔偏轴单向板的孔边应力计算公式，分析了一般铺层层合板受到复杂载荷作用时孔边的应力集中情况。

工程设计中，复合材料层合板往往会在较复杂的载荷条件下工作，包括面内两个方向的拉伸或压缩、面内剪切应力，甚至有弯曲载荷，而目前复合材料破坏准则主要以复合材料单层的正轴(即纤维方向和垂直方向)应力为基础进行层合板强度计算[4]。因此，含孔复合材料层合板在受到复杂载荷作用时，对其孔边各单层的应力和强度进行估计十分必要。

目前，工程设计人员一般采用ANSYS等商用有限元软件进行复合材料层合板的应力强度计算。对于孔边应力集中问题，为获得可靠的计算精度，必须采用密集网格，而网格划分和后续的有限元计算均需消耗较长时间，工作效率较低。本文探索了一种计算复合材料层合板孔边单层应力的方法，其计算过程相对简单，计算结果与ANSYS软件结果具有相当的计算精度，为工程设计人员提供了一种可选的复合材料层合板及孔边应力及强度分析方法。

2 复合材料层合板上圆形孔边应力计算

复合材料层合板受到面内载荷作用时，其孔边不同铺层角的单层正轴应力计算流程如图1所示。

图1 层合板孔边单层正轴应力计算流程图Fig.1 Calculation flow chart of normal axial monolayer stress at hole edge

复合材料层合板由多个不同铺层角的复合材料单层铺叠而成，其强度和刚度均可由单层强度、刚度性能叠加计算。由单向层合板工程弹性数据(纵向拉伸模量E1，横向拉伸模量E2，剪切强度G12，主泊松比ν1，单层铺层厚度h0)，可计算复合材料单层的正轴刚度模量和全局坐标下的偏轴刚度模量。复合材料层合板的面内刚度矩阵[Aij]可由下式确定[4]：

式中：υα为铺层角为α的单层的层数比例，(i，j=1，2，6)为铺层角为α的单层的模量分量。

将复合材料层合板简化为均匀各向异性板，其工程弹性常数可由层合板的面内柔度系数[Sij]计算得到：

当含圆形孔的各向异性板受到σx、σy、τxy作用(图2)时，孔边仅有周向应力σθ，径向正应力和面内剪切均为0。采用叠加原理，σθ由下式确定[5]：

公式(3)计算的孔边中面平均应力为局部极坐标下的应力，需转化为全局坐标系xOy下的应力，坐标转换矩阵为Tθ。

复合材料层合板单层正轴应力是强度计算的关键。需将全局坐标下的孔边应力转换为在单层局部坐标系下的正轴应力，转换矩阵为Tα，如式(4)所示。

式中：下标L、T分别表示纤维方向和面内垂直纤维方向。

图2 含圆形孔的各向异性板受复杂载荷示意图Fig.2 Anisotropic plates with circular holes subjected to complex loads

因各向异性板为复合材料层合板简化而来，故式(4)中的柔度矩阵[Sij]即为式(2)中的柔度矩阵。得到不同单层孔边正轴应力后，即可进行复合材料层合板孔边强度分析。

3 算例分析

采用有限元软件ANSYS为参考工具，与本文所述方法进行对比分析。假设某一无限大复合材料层合板由单向复合材料铺设而成，单层材料厚度为0.125 mm，铺层数共20 层(0h，8 层；90h，4 层；45h，4层；-45h，4 层)，层合板总厚度为2.5 mm。层合板所受载荷σx=100 MPa、σy=50 MPa、τxy=20 MPa，其中层合板x轴与0h方向一致。

有限元计算模型为20.0 mm 宽的正方形板，其中心有一直径为1.0 mm 的圆形孔洞，对孔边施加相应载荷并进行求解。单层复合材料的力学性能为：E1=136.7 GPa；E2=8.2 GPa；G12=4.5 GPa；ν1=0.294；纵向拉伸强度XT=1 604.9 MPa；纵向压缩强度XC=1 305.7 MPa；横向拉伸强度YT=40.5 MPa；横向压缩强度YC=239.7 MPa；面内剪切强度S=84.0 MPa。

分别使用本文方法和ANSYS 软件计算层合板孔边应力分布，图3 示出了层合板中0h层孔边正轴应力分布。图中，横、纵坐标分别表示应力点所在位置的角度和应力。可看出，两种方法计算结果吻合度较高，从-180h到180h的整个孔边应力的变化趋势均契合良好；但在应力变化的极值位置附近均存在差异，具体表现为本文计算方法在极大值位置应力高于ANSYS软件计算结果，在极小值位置应力低于ANSYS软件计算结果，即本文计算方法结果曲线变化率比ANSYS软件计算结果的大。分析认为，这是因为ANSYS软件计算结果受到其网格密度限制，在应力变化十分剧烈的区域不足以表达所致。

图3 层合板中0h层孔边正轴应力分布Fig.3 Stress distribution of hole edge in 0hlayer in laminated plates

为进一步分析本文计算方法的有效性，对层合板四个不同铺层角的孔边进行强度分析，采用蔡吴失效准则计算蔡吴数，结果如图4所示。可看出，对于0h、90h、45h、-45h四个不同铺层角的子铺层，两种方法计算结果有较好的吻合度，从-180h到180h的整个孔边蔡吴数的变化趋势均十分契合。最大蔡吴数出现在-45h层，ANSYS软件计算结果中最大蔡吴数为0.93，本文方法计算结果中最大蔡吴数为1.06。

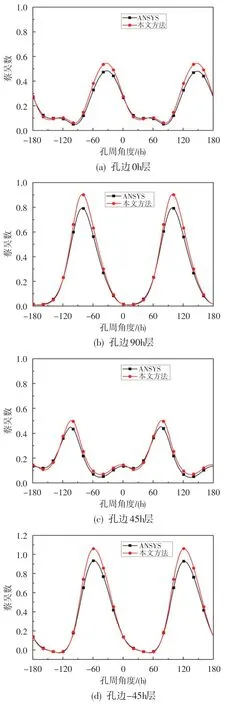
图4 层合板中不同铺层角孔边的蔡吴数Fig.4 Tai-Wu number of hole edge with different angle layers in laminated plates

复合材料层合板开孔问题多采用应力集中系数的概念进行研究[6-11]。通过本文方法计算可明显发现，层合板孔边相同位置不同铺层角的单层正轴应力有明显区别，如图5 所示。铺层角为0h的单层纤维方向应力(σL)的最大绝对值出现在8hi 90h位置，为610 MPa；而铺层角为90h的单层σL的最大绝对值出现在i 90h的位置，为703 MPa；铺层角为45h的单层σL的最大绝对值出现在i 90h位置，为123 MPa；铺层角为-45h的单层σL的最大绝对值出现在90hi 23h和-90hi 23h位置，为117 MPa。

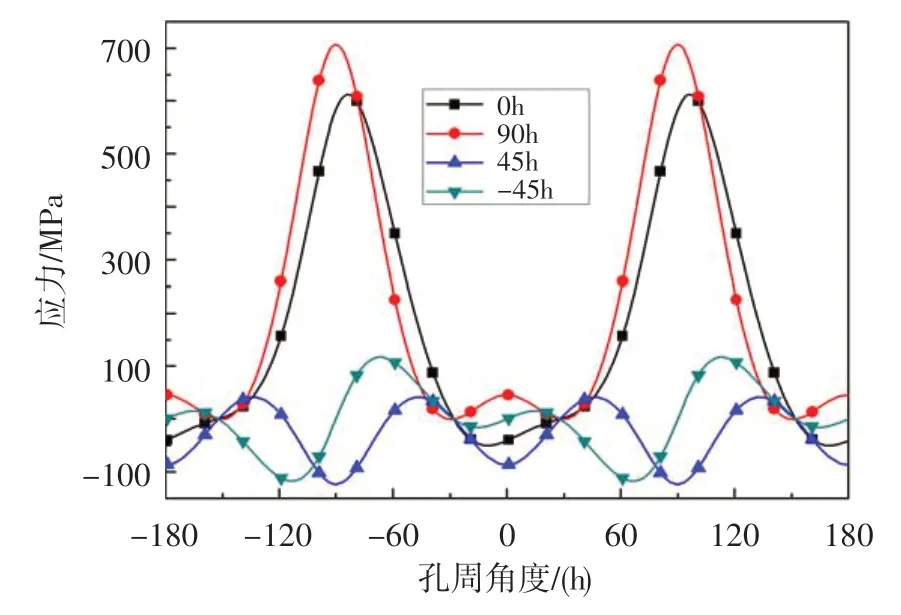
图5 层合板孔边不同铺层角的单层纤维方向应力分布Fig.5 Stress distribution of hole edge with different angles of laminated plates

综合前文的应力计算方法和列举的算例，对于复合材料层合板开孔结构的应力分析，工程设计人员可结合目前使用的有限元方法，在假设无开孔的情况下计算层合板开孔位置的平均应力，然后采用本文方法进行开孔位置孔边单层应力补充计算及强度预估，分析过程相对于直接采用有限元软件明显简化，从而提高工作效率。

4 结论

(1)本文计算方法可较好地反映层合板中圆形孔边不同铺层角的单层正轴应力分布，且应力和强度分析结果与ANSYS软件计算结果的精度相当。

(2)层合板孔边相同位置不同铺层角的单层正轴应力各不相同，需要分别进行应力和强度评估。

(3)本文将层合板孔边应力分析细化到了单层的程度，但对于有限宽层合板的边界对孔边的影响、开孔区层间剪切效应的影响、椭圆及其他形状开孔的计算、层合板受到弯曲载荷作用时孔边应力的计算等几个问题，都影响了本文计算方法的精确性和适用性，需要开展进一步研究予以解决。