高耸结构断裂后倾倒过程的动力学分析1)

牛清勇 曾国伟 郑华升

(武汉科技大学理学院，武汉430065)

问题高耸结构断裂后的倾倒问题可以简化为图1(a) 所示的力学模型。已知结构断裂后分成了相互铰接的两部分，上部结构在重力的倾覆力矩作用下无初速倾倒，下部结构与地面固结始终保持静止。若上部结构倾倒后的位置用其轴线与铅直方向的夹角φ来表征，且上下两段均视作均质细长杆。试分析上部结构倒落至某一位置所需的时间和基础的动约束力。

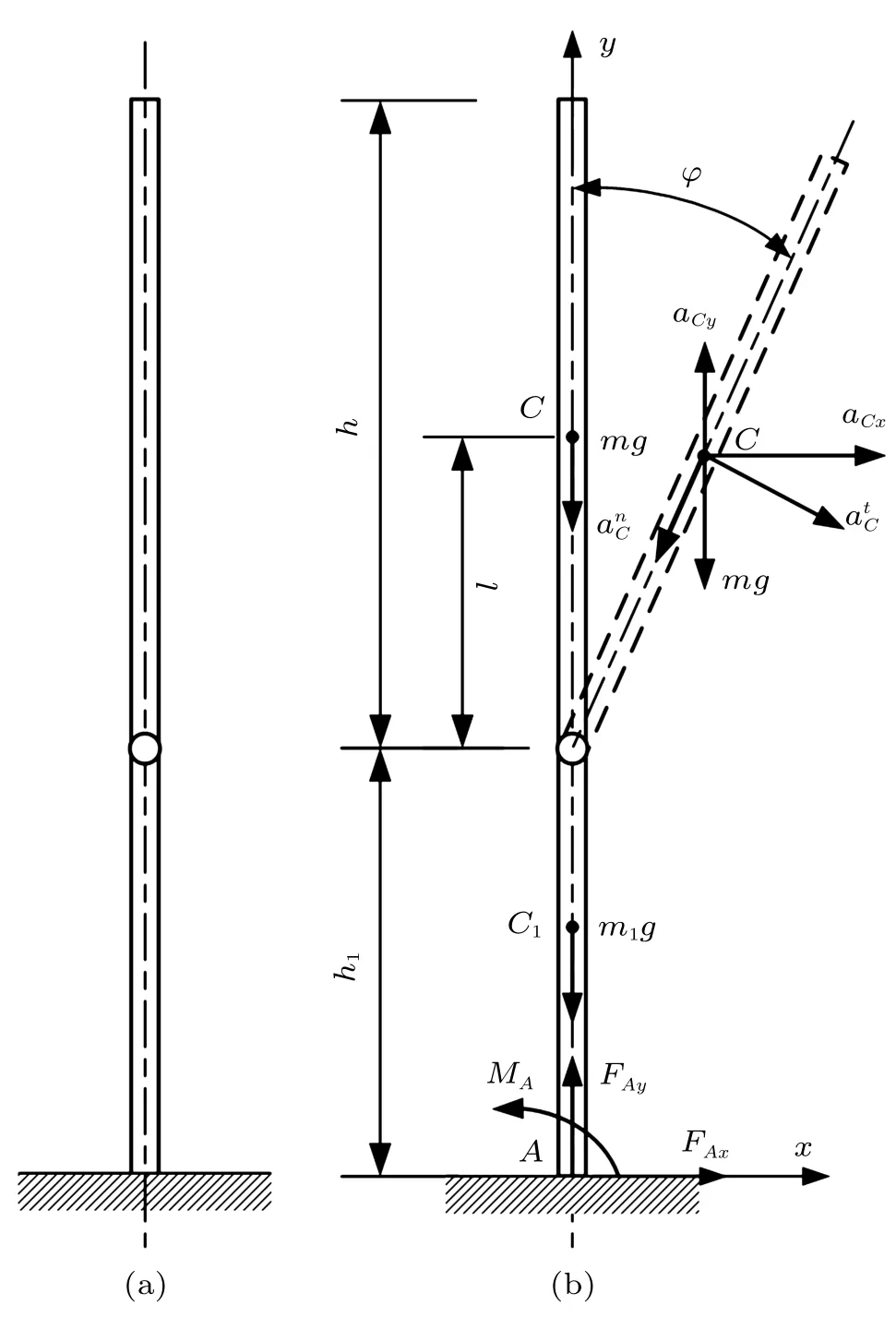
图1 高耸结构倾倒分析模型

解答针对目前理论力学教材[1-3]在动力学部分中还缺少有关细长杆倾倒时间分析的现状，本文试着做一些探讨。高耸结构如水塔、烟囱、桥梁的桥墩或主塔等，在拆除过程中常会遇到中部断裂后的倾倒问题，可将上述过程简化为图1(b) 所示力学模型来分析，其实质上是个特殊的一级倒立摆。上下两段结构的长度、质心位置、上部结构倾倒后的运动分析以及下部结构固定端处的受力分析已在图1(b)中给出。设上部结构绕断口的转动惯量用JO表示，当其从竖直位置(初始倾倒角φ0= 0◦) 无初速倾倒至任一位置φ时，根据动能定理有

利用二倍角公式，式(1) 可以表示为

考虑到角速度为正，整理式(2) 有

由式(3) 可得到关于倾倒时间t的微分表达式

将式(4) 从φ0到φ积分，当0< φ0< φ≥90◦可以得到

注意到∫csc(x)dx= ln(|tan(x/2)|)+ C (此处C 为积分常数)，则可以得到倾倒时间的显式表示

上部结构由竖直状态倾倒至任一位置φ时的角速度ω可由式(1) 推出

将式(2)两边同时对时间求导并消去角速度项，可得到角加速度为

上部结构质心C的加速度可表示为

将式(8) 的切向和法向角加速度分别向x和y轴分解并合成后，得到直角坐标形式的加速度

对系统整体利用动量定理并对断口截面Oz轴应用动量矩定理，可以解出基础的约束力结果

利用式(6) 和式(10) 可以对高耸结构断后的倾倒时间和基础的动约束力进行分析。

(1)固定倾倒末位置φ为某一定值，同时变化初始倾倒位置φ0，可得到结构从不同初始位置φ0倾倒至当前位置φ所需要的时间。如令φ=90◦(即倒至水平位置) 并且将式(6) 无量纲化，则无量纲倾倒时间随初始倾倒角φ0的变化规律如图2 所示。

由图2 可以看出，倾倒至水平位置φ= 90◦所需的时间依赖于倾倒的初始位置φ0。初始倾倒角φ0越小，则倒至水平位置所需的时间越长。当φ0趋于0◦时，倾倒所需的时间也趋于无穷大。这是因为φ0= 0◦位置为上部结构的铅直平衡位置，除非受到干扰平衡被打破，否则上部结构将一直保持平衡不会倾倒。由于结构断口余留截面形心和上部结构质心连线与铅垂方向的夹角通常不等于0◦，因而存在倾覆力矩，所以断裂后的倾倒时间常为一有限值。

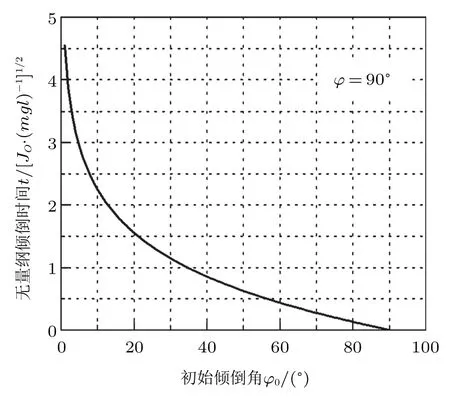
图2 倒至水平位置所需时间与初始倾角的关系

(2) 假设断后的上部结构从铅直位置开始倒落，根据式(10a)∼(10c)，绘制出无量纲形式的动约束力随倾倒角度的变化曲线，如图3 所示。需要指出的是，竖直约束力分量中扣除了结构自重的影响，为附加形式的动约束力。水平动约束力和动约束力偶的变化规律完全相同，数值上仅相差下部结构的高度h1。由式(10a) 和式(10c) 可知，在φ= arccos(2/3)(即48.2◦) 前后，水平动约束力和约束力偶的方向会发生反转，并且此后它们的大小随倾倒角度的增加而增大。竖直附加动约束力的大小随倾倒角度的变化呈现下凹形状，由式(10b)可知在φ=arccos(1/3)(即70.5◦)处，基础的竖直附加动约束力取到极小值。

图3 倾倒过程基础中的附加动约束力