考虑用户偏好的城区电动汽车充电站选址定容优化研究
张轶伦 黄剑秋 戴佳炜
(上海交通大学机械与动力工程学院, 上海 200240)
1 引言与文献综述
众多学者对电动汽车充电站选址定容问题从多个角度展开了研究,此类问题的主要研究方法分为聚类方法、启发式方法和优化类方法。
在聚类方法方面,冯瑛敏等基于给出的上下限,通过层次聚类、中心聚类等方法直接得到选址决策[1]。赵书强等采用Voronoi 图划分每个充电站所服务的负荷区[2];同时,也提出了启发式方法进行充电站选址。作者认为用户可根据最短路计算结果进行就近选择,并在此基础上采用差分进化粒子群方法得到布局规划结果[3]。类似地,Bai X 等以最小化客户行驶和充电时间成本为目标,考虑客户需求在不同站点的分流规律,设计基于NSGA-II和邻域搜索的启发式方法对问题进行求解[4]。
在优化类方法中,熊虎等基于Voronoi 图和排队论,考虑快充站点能力和需求的随机性,分析了电动汽车公共充电站布局规划问题[5]。刘文霞以减少客户等待时间和降低充电站投资成本为目标,建立排队论模型对拥堵地区客户平均队列长度及等待时间进行了分析,提出了快充站点设备优化和容量调整方法[6]。Xie F等同时考虑每个OD(Origin-Destination)对路径和站点的匹配,以及充电的起止点;用排队论描述随机的充电行为,并采用基于仿真的优化框架设计遗传算法[7]。对于此类随机性问题,部分学者采用鲁棒优化方法进行求解[8]。同时,也有学者从多层规划的角度进行建模。段豪翔等采用双层规划方法开展研究,以体现充电站与配电网规划的协同性[9]。Liu H和Wang D Z W建立了三层规划模型,第一层是根据成本来定位;第二是客户根据去充电的金钱成本、时间成本和距离成本,按概率筛选;第三,多客户的均衡[10]。
在建模时有以下几个重要因素值得考虑:成本、客户选择、服务水平。成本的定义是多元化的,主要包括时间和空间等角度[11-12]。例如,Arslan O和Karaan O E同时考虑城区内和道路上的充电站布局问题,以距离成本为目标,建立数学模型并进行求解[13]。客户选择方面,主要通过建立效用函数来衡量客户选择偏好[14]。Li J 等认为,客户的行为包括搜索行为和充电行为。在此基础上,利用贝叶斯推测的方法来预测需求[15]。Yang W 采取了基于OD的需求建模方式,并以此为基础来衡量客户的选择情况[16]。Cavadas J 等定义了与距离负相关的效用值,并认为客户选择的依据是以需求和该效用值相乘,在此基础上建立了静态需求下的选址定容模型[17]。服务水平方面,一类比较常见的方式是以平均充电距离来衡量[18]。
通过上述分析不难看出,目前学界对于该领域问题的研究主要依赖传统的优化方法,缺少从数据中提炼的规律。建模过程中一般假设需求遵循某已知统计分布,进行求解随机规划问题。此外,现有文献较少对客户的特点和行为偏好做全面的刻画,即客户画像;更缺乏基于客户细分的决策优化过程。
因此,本文相比于当前其他研究,将主要在客户行为偏好方面进行探究,并将数据中体现的规律与传统优化模型相融合。首先,对客户进行聚类,基于客户细分来描述不同类型客户的偏好和充电行为规律。在此基础上,发现客户在充电结束后均对充电桩有不同程度的占用,因此提出“能力折扣”的概念,更加贴近现实情况。此外,定义供需比作为给定站点、充电桩种类和时段后的服务水平,方便政府决策者在充电站布局规划时进行参考。本研究以最小化充电站建设成本和最小化客户充电成本为目标,考虑客户细分、能力折扣、桩选择偏好、预算限制、容量限制、服务水平限制等因素,建立混合整数线性规划模型,对单阶段选址定容问题加以求解,得出各备选站点各种充电桩的建设容量。
2 数据分析
由于本文基于实际数据进行研究,故需先对数据集进行探索分析,以此为数学建模提供参考依据。
由于公共类充电站数量远高于其他类别充电站数量(如图1所示),故为方便起见,本研究只关注公共类充电站。
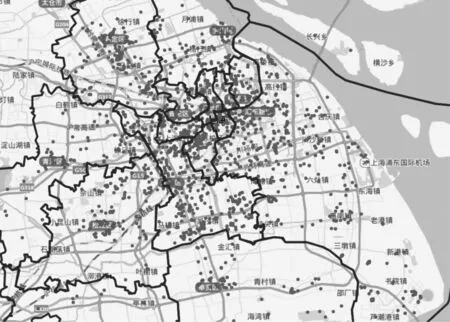
图1 上海市公共类充电站分布图Fig.1 Distribution of public charging stations in Shanghai
而后进行三方面的数据分析:充电设施布局情况、充电站利用率情况、充电行为分析等,下文将分别加以描述。
2.1 充电设施布局情况
主要按行政区对各区域的充电站分布情况进行分析评判。由于浦东新区网点布局规划最为合理和成熟(如图2所示),故这里以浦东新区为例进行展示。

图2 浦东新区充电站分布图Fig.2 Distribution of charging stations of Pudong District
2.2 充电站利用率情况
以某个充电站内每天每根桩的充电次数和充电工作时间这两个指标,来衡量该充电站的利用率情况,大部分充电站不存在排队等待情况,因为其利用率不高。这里展示利用率较高和较低的实例,如表1所示。

表1 站点利用率实例Table 1 Charging station utilization
由此可知,需要考虑站点(或充电桩)的服务水平,该指标应与充电站服务能力和充电需求的比值相关。设置服务水平限制,以避免部分站(或桩)的服务能力在某个时段不满足需求。
2.3 充电行为分析
车辆行驶和充电记录中给出了充电开始时间、充电结束时间、初始SOC、结束SOC、充电量、充电时长;并可以在此基础上计算距离上次充电完成的时间和距离、最大功率、平均功率、所使用的充电桩种类(快充或慢充)。这些特征共同描述了充电行为规律,并可对后续建模提供相关参考和依据。
2.3.1 时段划分
由于需求呈现时变性,则选址定容模型必须考虑时间这个维度。本问题中,以开始充电时间为依据对时段进行划分。为保证使得各时段之间区别较为明显,根据对各个车辆的开始充电时间的频数分布统计,划定时段为:t=1, 22:00-4:00;t=2, 4:00-10:00;t=3, 10:00-16:00;t=4, 16:00-22:00。
2.3.2 能力折扣
对比车辆行驶和充电记录中的充电时长,和充电站使用记录中的充电桩占用时长,可以发现存在充电桩无效占用的情况,即没有充电但是车仍然停放在充电位上。这会严重影响充电站的服务能力,在设计模型时必须对“能力折扣”的现象引起重视。其中,充电桩理论充电能力打折的程度用一个系数表示,定义为有效工作时间/总占用时间。
2.3.3 客户聚类
使用层次聚类方法对纯电动车和混动车分别进行聚类,每类车(客户)的输入特征包括:充电开始时间处于4个时段的频率,初始SOC平均值,使用快充桩频率,充电电量平均值、方差、四分位点,充电时间平均值、方差、四分位点,距离下次充电时间的平均值、最大值,距离下次充电距离的平均值和最大值。层次聚类方法示意如图3所示。
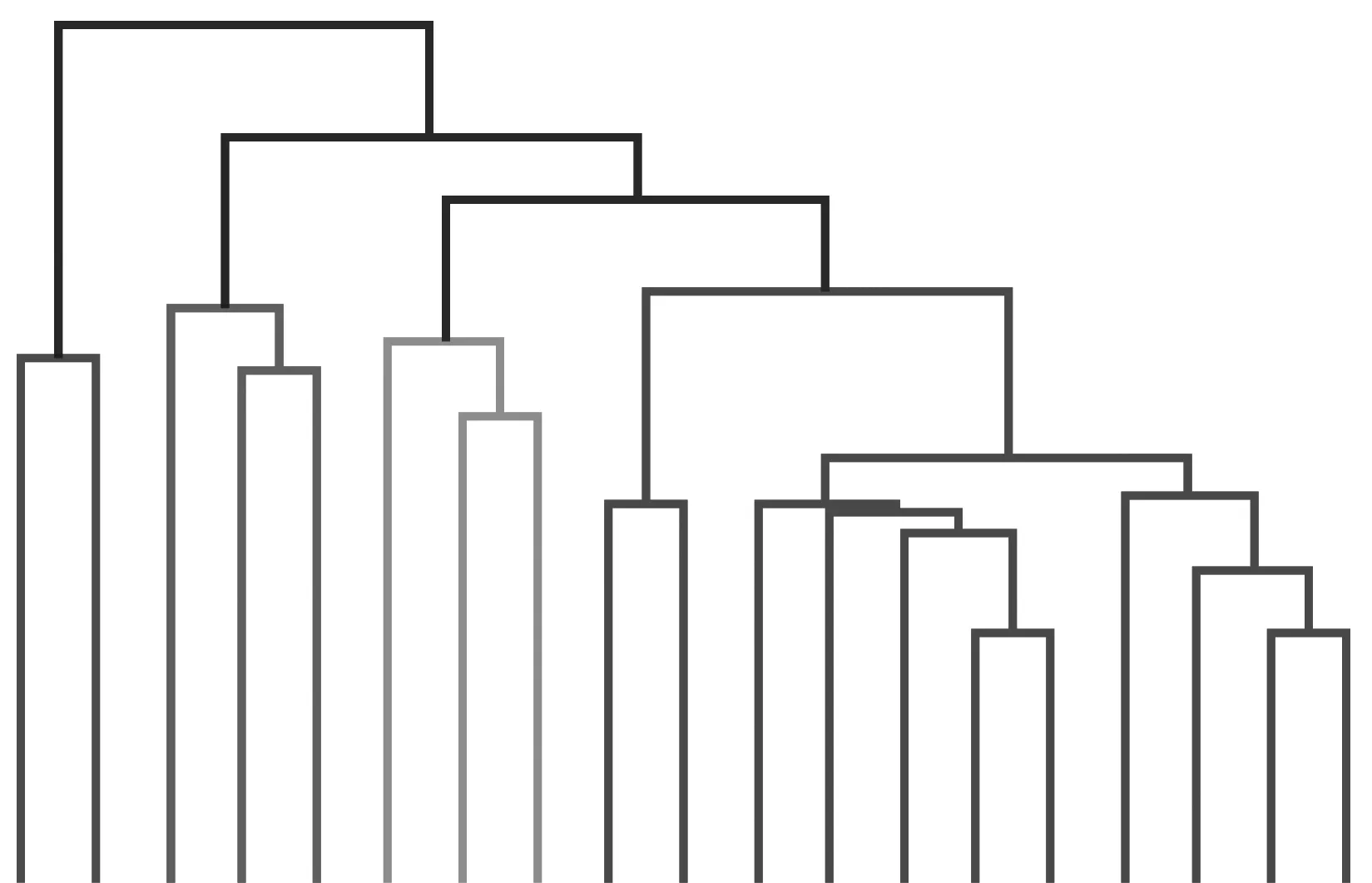
图3 层次聚类示意图Fig.3 Hierarchical clustering
为方便计算,同时保证各类之间的差异性,本研究中纯电车和混动车分别各自聚成4类,聚类结果和数值特征如图4、表2和表3所示。
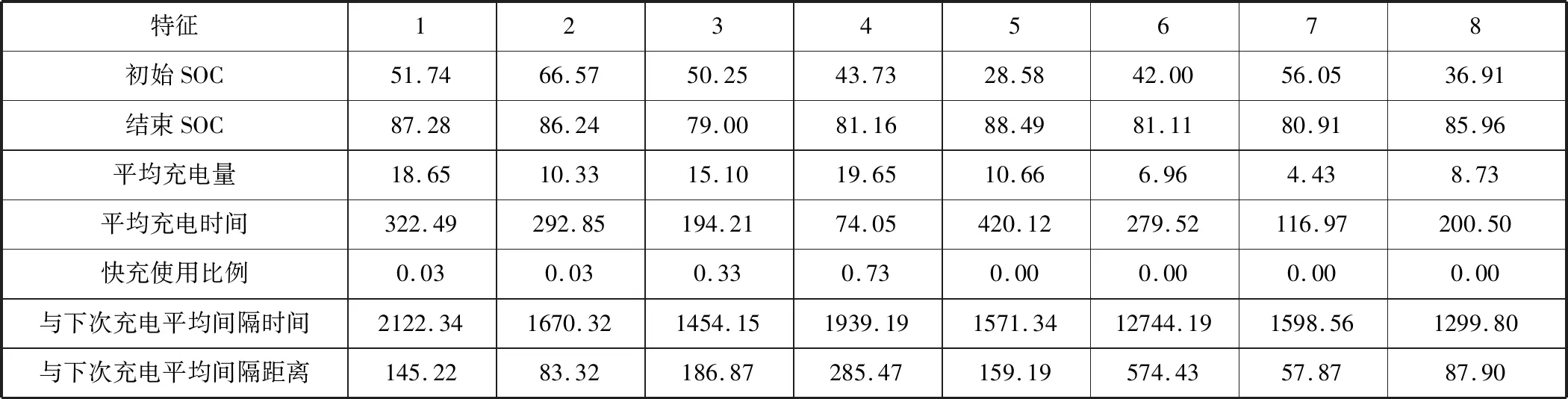
表3 各类客户数值特征Table 3 Numerical characteristics
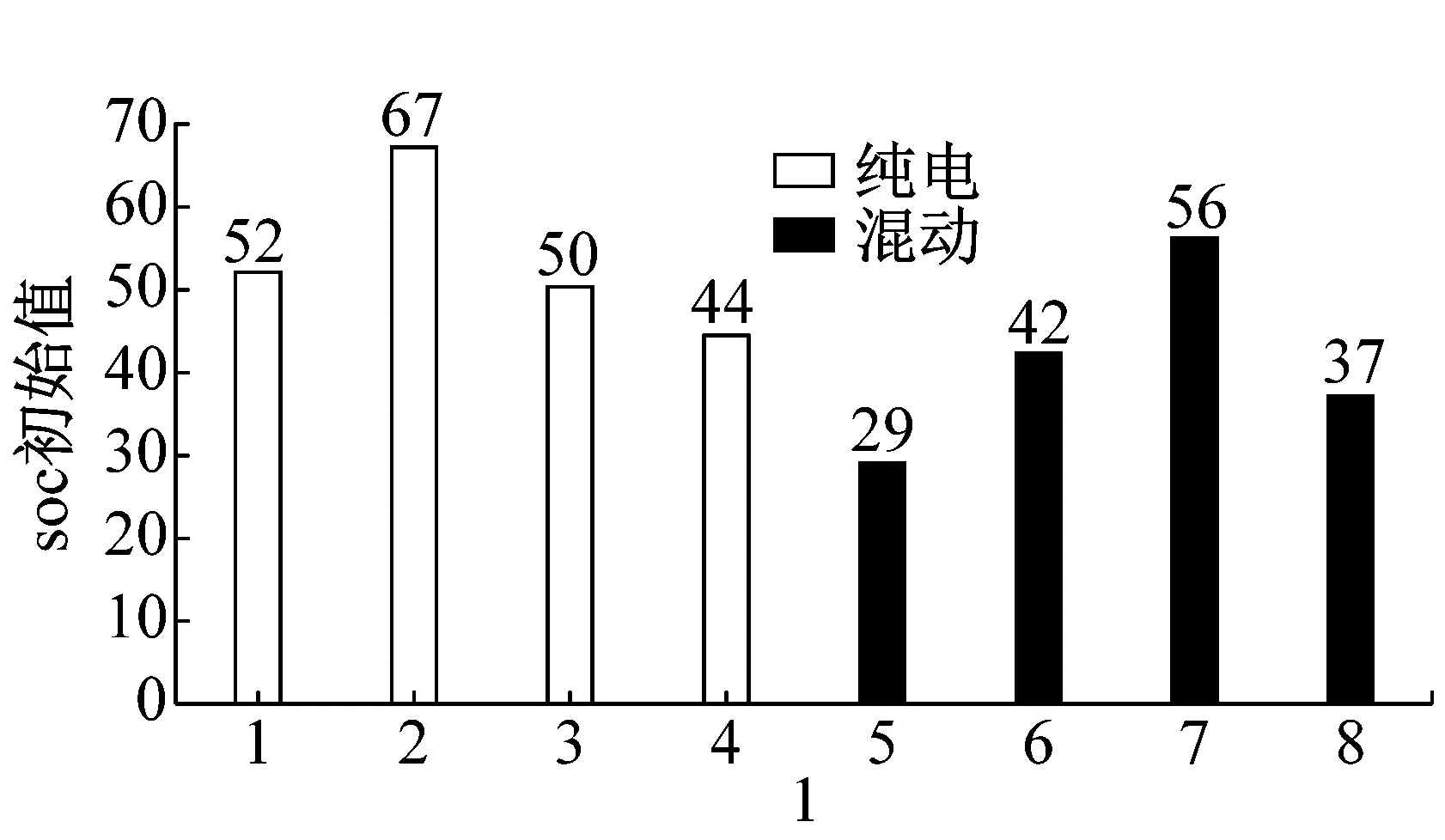
图4 客户聚类结果Fig.4 Customer segmentation result

表2 客户聚类结果Table 2 Customer segmentation result
完成客户聚类后,在数学建模过程中和参数计算时,都应注重各类客户之间的区别,这也是对客户偏好的考虑。
3 数学模型
本章将在文献综述和数据分析的基础上,对充电桩选址定容问题进行具体描述,并介绍数学模型。
3.1 模型参数
首先给出数学模型中所需的各项索引。对于一个给定的区域,根据地理信息划分I个客户聚集区,每个聚集区用i标识,其中i=1, 2, …,I。该区域内有J个备选的站点位置,备选站用j标识,其中j=1, 2, …,J。在任何一个客户聚集区,都可能存在最多K类客户,下标用k标识,其中k=1, 2,…,K。如前文所述,客户类别根据充电行为偏好进行聚类得到;同时所有k组成的集合又可按照纯电车和混动车分为两个子集,分别是Uelectricty和Uhybrid。提供Q种充电桩供客户选择,下标用q标识,其中q=1, 2, …,Q;根据实际情况,仅考虑两种充电桩,q=1表示慢充,q=2表示快充。由于需求具有时变性,故需要引入时段的概念,以下标t标识,其中t=1, 2, …,T。
而后,定义如下参数,如表4所示。

表4 模型参数表Table 4 Model parameters
3.2 决策变量、目标和约束
3.2.1 决策变量
Njq为非负整数,表示第j个备选站中第q种充电桩的数量。同时定义辅助变量Pijkt和Yijk。其中Pijkt为取值为[0,1]的连续变量,表示第t时段第k类客户从聚集区i到备选位置j充电需求,占第t时段在聚集区i的第k类客户充电总需求的比例。Yijk具体定义如下:
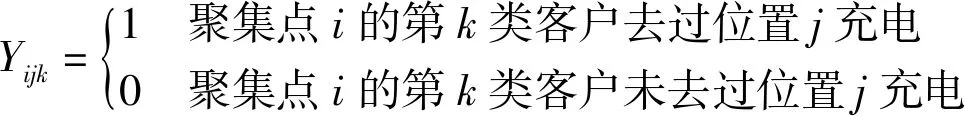
3.2.2 目标函数
(1) 充电站建设成本
成本包括在备选位置j建站的固定成本,和充电站中设置不同种类充电桩的可变成本。
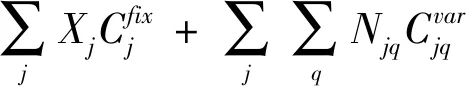
(2) 客户充电成本
本模型中的客户充电成本只和距离相关,该目标具体表示如下:
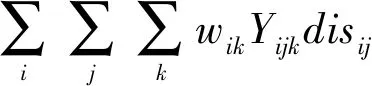
综上,最终目标表达式为:
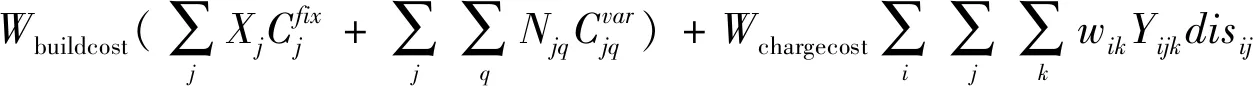
3.2.3 约束条件
(1)Njq与Xj的关系
如果某个位置建设任意一种充电桩,则该地一定建设充电站。反之,如两种充电桩均未建设,则说明此地不建设充电站。

(2)Yijk与Xj的关系
如果对于所有聚集区的各类客户,都没有被分配到某个备选站,则该地不建设充电站;否则,需要建设充电站。
(3)Yijk与Njq的关系
从数据中可以发现,混动车只能使用慢充,因此如果一个站点没有慢充桩,则不能为混动车提供服务。
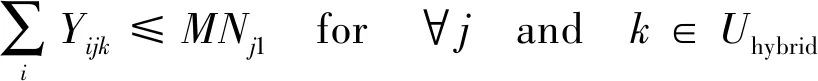
(4)Pijkt与Yijk的关系
指定某个聚集区和客户类型,如果在每个时段都没有需求被分配到备选站j,则说明该聚集区的该类客户不会由备选站j服务,反之亦然。
(5)Pijkt归一化
根据Pijkt定义,需要保证任意时段、某类聚集区的某类客户,被分配到各个备选站的需求比例和为1,即需求总会被分配到充电站。
(6) 服务水平要求
由于在建设规划不是一步到位的,因此在初期不可能满足所有充电需求,因此需对充电能力和充电需求的相对大小关系进行限制,即服务水平要求。
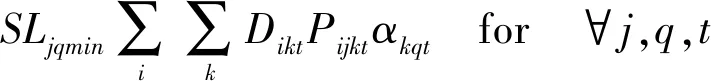
(7) 预算限制
考虑到充电网络布局规划时的经费要求,需设置预算限制,具体如下:
(8) 充电桩容量限制
考虑到城区规划要求、地区面积、电力配套设施和功率上限等方面的要求,应对不同区域不同种类的充电桩的数量加以限制,具体表示如下:
Njq≤capjqfor ∀j,q
(9) 客户聚集区与充电站的最大距离限制
考虑到车辆续航、服务半径要求,和城市基础设施建设对生活质量的影响,有必要限制每个聚集区的客户到充电站的最远距离,具体表示如下:
Yijkdisij≤Maxdiskfor ∀i,j,k
3.3 模型总结
综上所述,建立混合整数线性规划(MILP)模型对充电桩选址定容问题进行建模,数学模型如下:
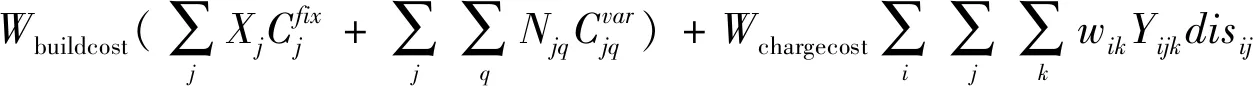
s.t.
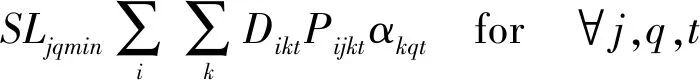
Njq≤capjqfor ∀j,q
Yijkdisij≤Maxdiskfor ∀i,j,k
4 数值实验
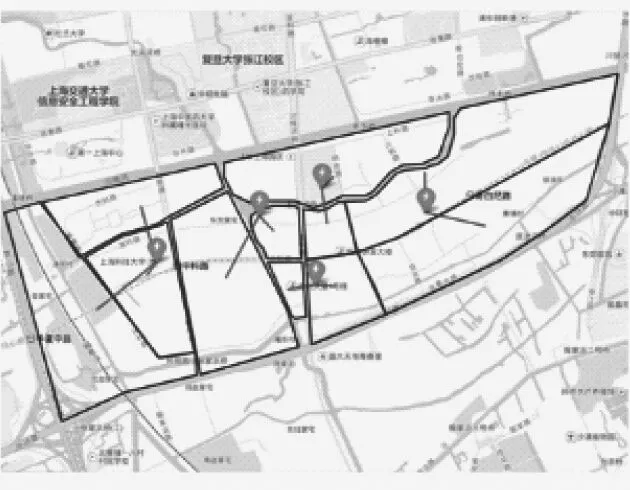
选取浦东新区某一地块进行数值实验,如图5所示。其中,蓝色或红色边框的为客户聚集区,共11个;红绿色同心圆为现有充电站,共11个;蓝色图标为其他备选站址,共38个。注意,在本实验中,备选站址包括现有充电站位置,共计49个,排序为未建站在前、已建站在后。
将随机生成的所有数据输入Gurobi求解器得到全局最优解,实际建设成本为1060.33万元,充电成本为24844米。表5给出了建站位置对应的充电桩数量。
表6给出每个地区每类客户和充电站的对应关系,即Yijk;表7更细致的给出了对应的Pijkt。

表7 每个地区每类客户和充电站的时间分配关系Table 7 Time distribution relationship between customers and charging stations
图6中,其中标红的是原来已有站点,标蓝的是未建站点(备选站址)。带橙色和黑色同心圆的表示本次规划中建站的地方,橙色圈的半径表示慢充桩的个数,黑色圈的半径表示快充桩的个数。
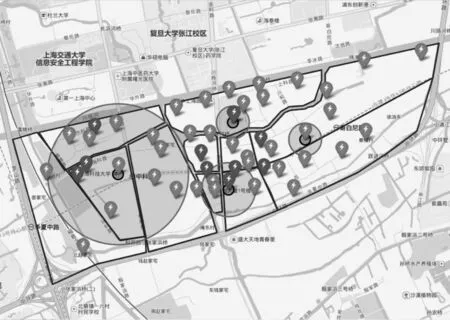
图6 布局规划结果Fig.6 Layout planning result
每个聚集区内的各类客户和充电站对应关系如图7所示。

1
从中可以发现,快充桩建设数量很少,这是因为快充桩选择比例较低,且需求总量较低导致的。为印证这一点,人为增加快充桩选择比例,保证大多数人愿意选择快充桩这个事实,同时将需求总量扩大(考虑五年后的需求),即可得到完全不一样的选址定容结果,如表8-10和图8-9所示。
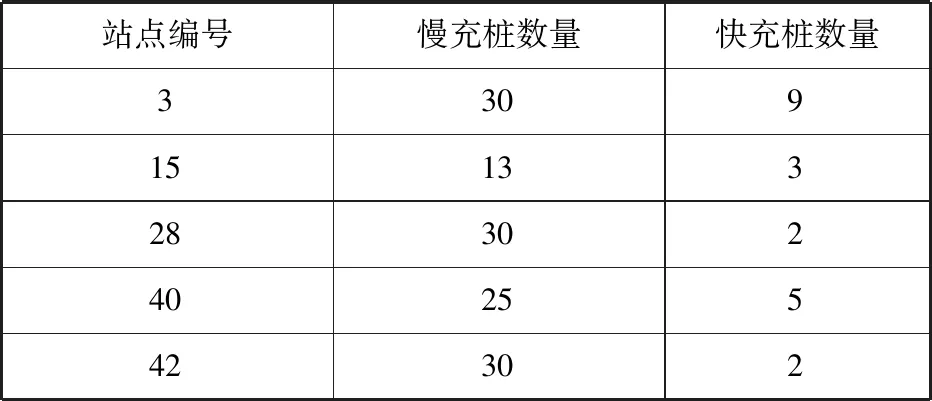
表8 建站容量Table 8 Capacity of charging stations
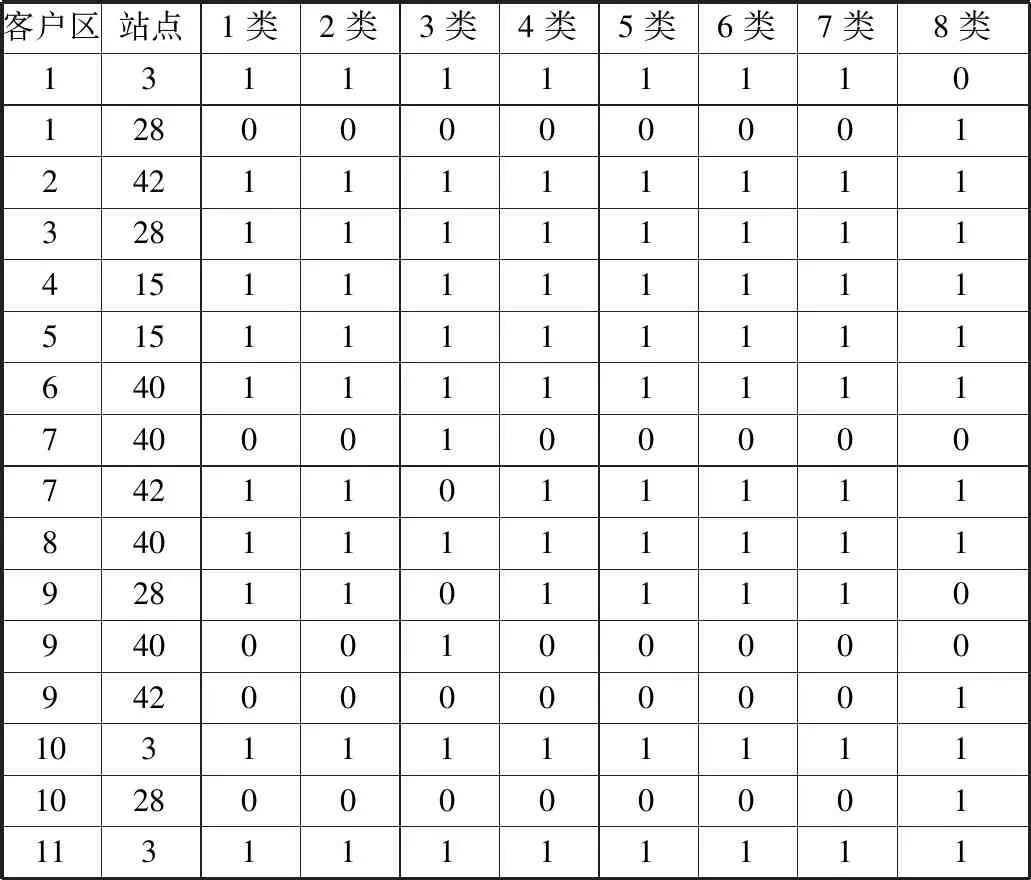
表9 每个地区每类客户和充电站对应关系Table 9 Mapping relationship with customers and charging stations
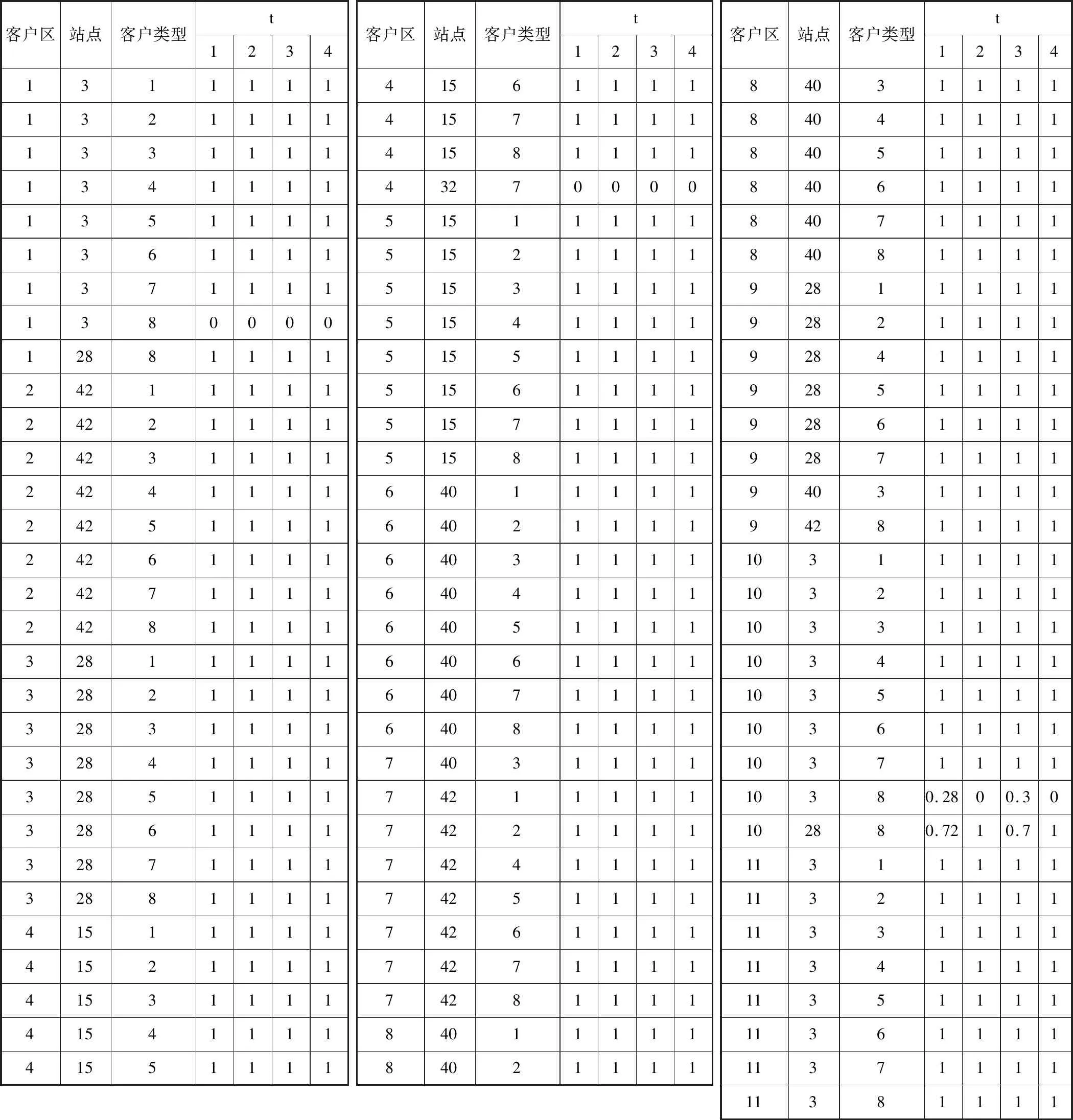
表10 每个地区每类客户和充电站的时间分配关系Table 10 Time distribution relationship between customers and charging stations

图8 布局规划结果Fig.8 Layout planning result
1
5 总结与讨论
本研究针对新能源汽车充电站选址定容问题展开研究,以最小化充电站建设成本和最小化客户充电成本为目标,考虑客户细分、能力折扣、桩选择偏好、预算限制、容量限制、服务水平限制等因素。由数值实验可以发现,在保证服务水平的前提下最大限度的减少了开销,这也体现了在未来实践中的重要价值。此外,本模型具有较好的扩展性,未来可以在多阶段布局规划、考虑随机性的选址定容问题等方面进行更深入的研究,求解更加复杂和多样的选址定容问题。

