基于光谱整形的三角波生成方法①

涂昭阳，文爱军，李祥瑞，李晓阳

(西安电子科技大学 综合业务网理论及其关键技术国家重点实验室，西安 710071)

0 引言

高速三角波波形在无线系统、光信号处理、雷达、液晶显示系统等诸多电子系统中有着重要的应用[1]。然而，受到电子瓶颈影响，当前的电子波形生成技术能支持的带宽一般小于20 GHz[1]。微波光子学是微波和光子学的交叉学科，利用光子技术可以解决微波领域难以解决或无法解决的问题[2]。光子学技术凭借其高频载波的特有优势，将微波信号搬移至光频段，能提供足够大的带宽。基于微波光子技术，研究人员提出了很多三角波波形生成方法。在这些方法中，外调制方法可以在较低的成本下实现全占空比波形，是当前学术界研究的热点[3-8]。

基于外调制法的三角波生成方案其基本思想是利用调制器的非线性现象产生高阶射频谐波，通过合理调控系统配置可以令基波和三次谐波满足一定关系，即可近似的构造出三角波波形。基于外调制法的三角波生成方案主要面临以下三个技术难点：

第一，为了构造谐波间特殊的幅度和相位关系，通常需要使用结构复杂的光调制器和RF电桥，然而宽带射频电桥的幅度和相位不平衡将限制产生的三角波质量，且偏压控制电路复杂；第二，通过调制器的非线性产生高阶谐波要求射频输入功率足够高，一般的RF振荡器需要搭配额外的RF放大器一同使用。此外，为了控制基波和三次谐波的功率关系，系统对输入RF功率敏感，当后续PD电路的幅频响应不平坦时，输入的RF功率需要做校正，而额外的RF功率控制也会增加实现成本和难度；第三，受光纤的色散效应，精细设计的谐波间幅度和相位关系极易被打破，意味着大部分基于外调制的三角波生成方案不支持三角波信号的远距离馈送，无法适用于光纤连接的分布式系统中[8]。

文献[6]提出了一种三角波生成方案，其各边带的幅度关系严格依赖外加射频信号引入的调制指数，且产生的三角波易受调制器偏压影响。文献[7]提出的三角波生成方案基于相位调制器，避免了偏压漂移问题，边带间的相位和幅度关系通过调控级联微环谐振器实现。然而，级联微环谐振器的调谐能力有限，幅度和相位不能独立调整，这意味着射频信号的功率也需要精确控制，增加了调控难度。文献[8]通过调整调制器偏压预补偿光纤色散，使得该方案适用于三角波的长距离馈送。然而，该方案需要采用带宽受限的90度射频电桥，这将限制生成波形的速率。

为了解决以上三个技术难点，在采用外调制技术的基础上，提出了一种基于光谱整形的三角波生成方法，该方案仅需要一个无需偏压控制的相位调制器，产生的RF谐波间幅度和相位关系通过傅里叶域光处理器完成。系统无需额外的RF电桥和RF放大器，且通过编程光处理器可以补偿光纤色散。傅里叶光处理器集成度高，可灵活编程[9]，使得整个三角波生成系统结构紧凑、稳定度高。实验结果表明，该系统可以生成重复率为10 GHz的三角波信号，并支持25 km光纤馈送。

基于光谱整形的三角波生成器的原理图如图1所示，系统包括了一个激光器、一个相位调制器、一个频域光处理器、一段普通单模光纤和一个光电二极管。假定连续波激光器的功率为E0，载频为ωc。激光器的输出光经过一段保偏光纤后送至一个相位调制器，相位调制器由一个单音的RF信号驱动，假定RF信号的频率为ωs。相位调制器输出的已调光信号可以表示为

(1)

其中m为RF信号引入的调制指数，可以看出，相位调制器输出的光信号包含了一系列光边带，这里其充当的角色就是一个简单的光梳生成器。

生成的光梳送至一个傅里叶域光处理器中，它基于硅基液晶(Liquid Crystal on Silicon，LCoS)技术[9]。傅里叶域光处理器通常包括一个光输入和多路光输出。大量的LCoS可以构成一个2维的像素阵列作为处理器的核心，输入光会先经过一段衍射光栅，后根据波差异会照射在不同的LCoS像素点上，每个像素点可以动态的调制光的幅度和相位，同时可以将光信号路由到任意的光出口，从而实现可编程的空间光调制能力。

回到方案本身，利用傅里叶域光处理器的频域处理能力，可以对光梳的各个谱线进行灵活的幅度和相位控制。保留光载波、正一阶边带和负三阶边带，其余光边带全部抑制，得到的光信号可以表示为

Eop=E0ejωct[α0J0(m)ejφ0+α1J1(m)ejωst+jφ1-α3J3(m)e-j3ωst+jφ3]

(2)

其中αi(i=0,1,3)分别为傅里叶域光处理器对载波、正一阶和负三阶边带的幅度调控因子，φi(i=0,1,3)分别为傅里叶域光处理器对载波、正一阶和负三阶边带的相位调控因子。

先忽略光纤带来的影响，直接对这个信号进行光电探测，并忽略直流项，得到的电信号可以表示为

i∞2α0α1J0(m)J1(m)cos(ωt+φ1-φ0)-2α0α3J0(m)J3(m)cos(3ωst+φ0-φ3)

(3)

将理想三角波信号进行泰勒展开，可以将其写作

(4)

可以观察到，三角波信号可以写成一系列正弦谐波信号之和，其中5阶及其他高阶项被忽略。只要一次谐波和3次谐波的相位和幅度满足一定关系，就可以用两个正弦信号叠加近似合成出三角波波形。将式3与式4对比，得到了基于光谱整形的三角波生成器中，傅里叶域光整形器的设置要求

(5)

其中，k取任意整数。现在考虑光纤传输的情况，由于光纤存在群速度色散，光信号经传输后各个频率分量间的相位关系会发生改变。对于三角波生成器来说，产生的三角波会发生波形失真。色散对n阶光边带引入的相位可以表示为[10]

(6)

其中，L为光纤长度，D为光纤色散值。此时，输出的射频信号可以表示为

i∞2α0α1J0(m)J1(m)cos(ωt+φ1-φ0+θ+1-θ0)-

2α1α3J0(m)J3(m)cos(3ωst+φ0-φ3+θ0-θ-3)

(7)

得益于傅里叶域光处理器的幅度和相位控制能力，可以对传输前的信号进行色散预补偿，这与光域色散补偿器的原理是一致的。此时，幅度条件不变，实现三角波传输的设置相位条件可修正为

(8)

其中，k取任意整数。

2 实验结果及讨论

根据图1所示的方案原理，我们搭建了实验系统。可调激光器(Yokogawa, AQ2200-131)输出的光载波波长为1551.2 nm，线宽为3 MHz，功率约为12 dBm。这个激光器的输出光纤不保偏，由于相位调制器对输入的光的偏振态敏感，在激光器输出和相位调制器间放置了一个偏振控制器，令调制器工作在最佳状态。当激光器和调制器的尾纤均设计为保偏时，可以避免这个偏振控制器的使用。调制器(Photline, MPZ-LN-40)的模拟带宽大约为33 GHz，半波电压约为6 V，插入损耗小于3 dB。矢量信号发生器(Rohde & Schwarz SMW200A)当做一个模拟射频源使用，仅输出一个频率为10GHz的单频率的射频信号，经射频线送至调制器的射频驱动口。实验中傅里叶域光处理器的功能由一个商用的产品实现，即菲尼萨公司的Waveshaper 4000A，其同样基于LCoS技术且具有四个可编程的光输出。本次实验只需使用单路输出，其他三口输出口空置。Waveshaper的输出与25km光纤相连，经一个宽带光电探测器后可以得到电信号。电信号的波形由一个80GSa/s的示波器(KEYSIGHT, DSOV334A)观测，它的模拟带宽为33GHz。

首先用光谱仪观测经相位调制器后的信号，光谱如图2中的红色实线所示。可以看出输出信号为包含了一系列的光边带的光频梳，这是符合我们预期的。实验中Waveshaper的分辨率为1 GHz，经测试其最窄处理通带约为10 GHz，这也是选择射频信号为10GHz的原因。经处理后的光信号如图2中的黑色实线所示，可以看出已成功的得到载波、正一阶边带和负三阶边带。这里提到的正负指的是频谱上的正负，因此与图中的方向刚好相反。比较处理前后的光谱可以看出，光信号衰减明显，这是实验仪器光接头的磨损导致。

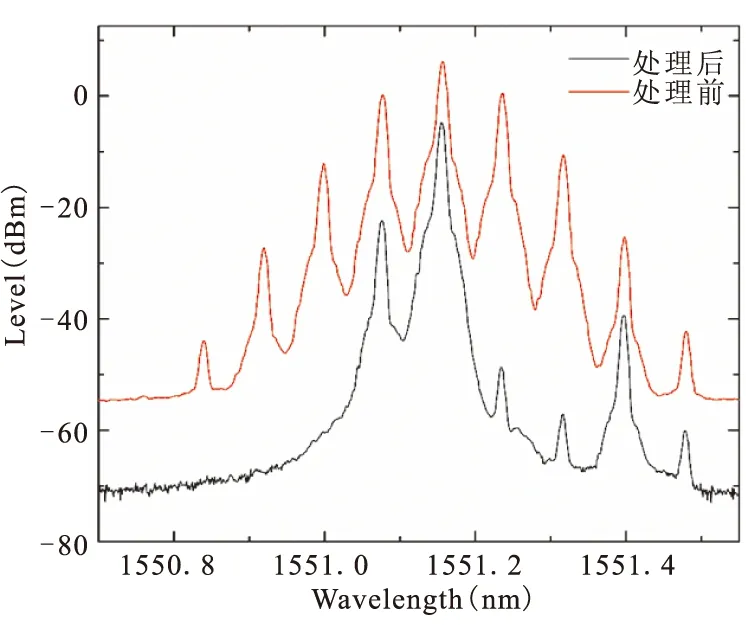
图2 光谱图，红实线表示相位调制器后的光谱图，黑实线表示经傅里叶域光处理器后的光谱图

经PD后可以得到三角波信号，其时域波形如图3所示。对示波器采集的原始数据进行去直流和归一化处理，如图3中的黑实心圆所示。以这组为参考，利用最小二乘法得到三角波的理想曲线。经过计算均方误差(Root-Mean-Square Error,RMSE)为0.057。采集更多的数据，采用Periodogram方法对该数据进行功率谱估计，得到信号的电频谱图，如图4所示，可以观测到一阶和三阶的功率比为19.6 dB，与理论值19.1 dB相近。频谱中同样存在二阶，这是因为光处理器的抑制比受限，不能完全抑制不想要的光边带，这个可以从图2的光谱图中看出。

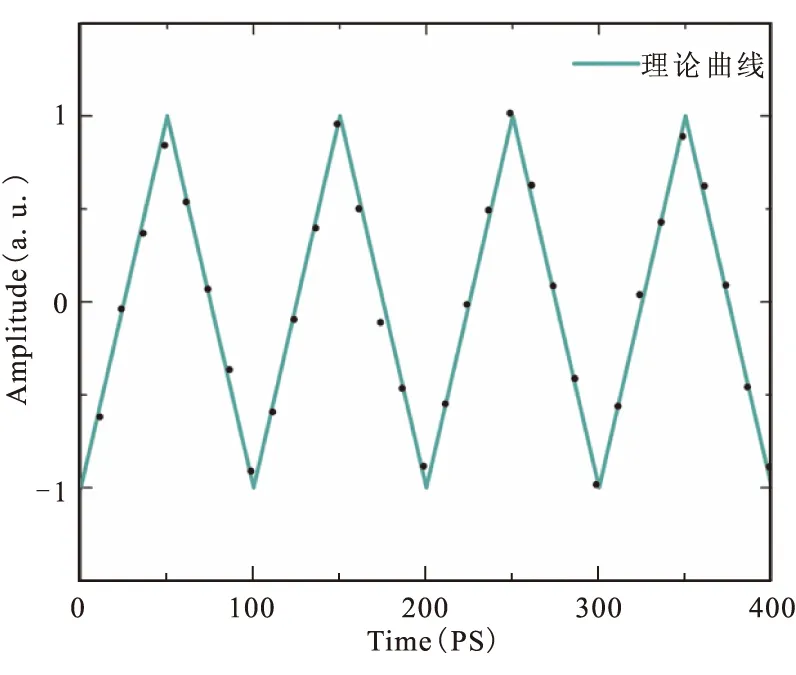
图3 生成的三角波时域波形图，RMSE=0.057

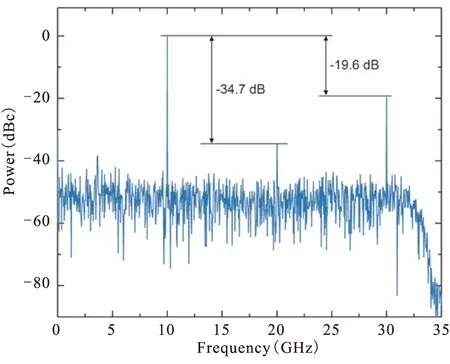
图4 生成的三角波电谱图

接下来测试三角波信号光纤传输的情况，我们在光处理器和PD之间插入25km光纤，但不对其他实验链路做调整。因为光纤距离较短，可以近似看做一个线性系统，根据理论分析，由于存在光纤色散，观测PD恢复出的三角波信号存在明显的失真，如图5(a)所示，经计算RMSE为0.108。

接着对光处理器进行重新编程，光处理引入的幅度响应不做调整，对载波引入的相移,用于补偿光纤引入的相位变化。图5(b)为经过补偿后的三角波信号，可以看出示波器的采集结果与理论曲线具有很好的拟合度，经计算RMSE为0.052，这个结果与不经光纤传输的三角波信号的RMSE结果相当。说明了基于光谱整形的三角波生成方案可以适用于光纤传输的情况。

实验中仅实现了10GHz的三角波信号生成，这是基于光谱整形的三角波生成方案能支持的最小重频，受光处理器的处理分辨率的限制。而更高重频的波形生成则仅受光调制器和PD的限制，本次实验由于示波器的模拟带宽仅为33 GHz，考虑三次谐波，能实现的最高频率为11GHz，这个频率与10GHz相近，故不作展示。

由于可以灵活控制边带的幅度和相位关系，该方案可以预补偿PD或后续电路的响应不平坦，这是其他三角波方案难以做到的。本文采用的Waveshaper为实验室用的LCoS商用仪器，实际工程使用会针对应用采用复杂度更低的LCoS芯片，并与整个光子系统共享一个温控设备，此时三角波产生系统的体积重量和功耗都得到很好的控制。

3 结论

本文给出了基于光谱整形的三角波生成方法，其仅采用一个相位调制器，通过傅里叶域光处理器可以灵活的调控光边带的相位和幅度关系，实测结果表明本方法可以在无需RF电桥和其他复杂RF器件的条件下实现10GHz重频的三角波波形生成，并支持25km光纤馈送。该方案的优点是调控灵活、系统结构紧凑且稳定度高。该方案的不足是，生成的三角波波形重频受傅里叶光处理器分辨率的限制，即最低重频为10GHz。然而，微波光子技术致力于解决大带宽、高重频的三角波信号生成难题，小于10GHz的低速波形完全可以通过传统电域波形合成方法实现。