共同配送中成本分摊问题研究
胡 琪
(北京物资学院,北京101149)
一、 引言
近年来物流行业的发展虽然一定程度上促进了物流设施的完善,但是也带来了物流资源的浪费。 为了降低物流成本,提高物流资源的利用率,共同配送这种模式逐渐兴起,共同配送的本质是将零散的客户聚集在一起进行共同送货,但如何将节约的成本进行合理的分配成为学者们的研究热点。
Göthe-Lundgren 等人在车辆路径成本分配问题中,利用集合覆盖模型计算出博弈的特征值,并运用约束生成方法求解出了核仁。 Engevall 等人将上述文章从单一车型扩展到多车型情况,同样运用约束生成求解核仁进行总成本的分摊。Åsa Hallefjord 等人研究了隐式给出特征函数值的合作博弈,即使是局中人的数量非常多的时候,也可以有效地算出核仁,为求解大规模情况下的核仁提供了有效的方法。 另一些学者对多配送中心的车辆路径成本分摊进行了研究,姜彦宁等学者为求解多仓库路径优化和成本分摊问题建立了一个双层的规划模型,第一层模型优化配送路径;第二层模型利用Shapley 值进行成本分摊。 王勇等人以总成本最小化为目标,运用最小最大费用收益分配模型求解收益分配方案,该方法可以提高联盟的稳定性。 Joen Dahlberg 等人研究了政府参与调控的VRP 模型,文中分别用Shapley 值、核仁和改进的EPM 进行了成本分配。 V.V.Zakharov 等人研究了大规模运输网络中运营商合作下的车辆路径问题,通过联合归纳算法构造了满足次可加性的博弈特征函数,最后利用Shapley 值和次核对成本进行分配。
以上学者的研究虽然比较广泛,也运用了合作博弈理论中的不同解方案,但是更多的学者倾向于使用Shapley 值,其原因可能是Shapley 值更容易计算,且突出了各个成员对联盟的贡献程度,但是Shapley 值有一个缺点就是可能不符合“个人理性”条件。 “个人理性”指的是局中人在联盟中的成本要小于局中人单干的成本,一旦Shapley 值给出的解方案不满足个人理性条件,局中人就有离开联盟的倾向,导致合作失败。 文章以极小化运输成本为目标,利用VRP 模型计算实施共同配送的总成本以及所有可能联盟的最小运输成本,以所有子联盟的运输成本作为特征值进行多种解方案的计算,如Shapley 值、核仁、τ值,并将多种解方案进行比较,选择出最合理的一种解方案。
二、 问题描述
文章考虑一个零售商、若干个顾客的情况。 零售商需要根据顾客的需求量向其供货,每位顾客的需求都是确定的常量。 不考虑零售商的库存能力,即认为其库存无限大,并且认为零售商的车辆数量不限且车辆型号相同,即每辆车的容量都相同。 不考虑顾客的订货成本及零售商的固定成本,以运输成本极小化为目标,对顾客进行分区配送,这实际上是一个车辆路径问题(vehicle routing problem,VRP)。 将每个联盟的极小化的运输成本作为博弈的特征值,计算不同解方案中每个顾客分摊到的成本。 为了简化问题,我们做出如下假定:
(1)顾客需要的商品相同,固定的时间段内需求是确定的。
(2)只有一家零售商,即顾客只能从该零售商订货。
(3)每位顾客的需求不超过车容量,所有顾客的需求量之和大于车容量。
(4)零售商和顾客都是理性人。
三、 模型建立
(一)合作博弈特征值构建
合作博弈中最为关键的就是构造博弈的特征函数,特征函数会对求解方案的结果产生一定影响,文章为了简化计算,用特征值替代特征函数。 首先,定义如下符号:
N={1,2,…,n}为局中人集合;
S表示N的任意一个非空子集,即∀S⊂N,S≠∅;
c({i})表示局中人i单干时的成本,文中简写为c(i);
c({S})表示联盟S形成后的成本,文中简写为c(S);
c({N})表示大联盟N形成后的成本,文中简写为c(N)。
论文博弈的特征值只考虑运输成本(与距离有关),通过建立VRP 模型,计算出顾客组成所有可行联盟的最小总成本即为博弈的特征值。 当局中人个数为N时,共有2N个子联盟,其中包含1 个空联盟,空联盟的特征值定义为c(∅)=0,最终有效的联盟应为2N-1 个。 为了建立VRP 模型,我们定义如下符号和变量:
V表示点集,包括仓库和所有顾客;
cij为点i到点j的运输成本,i=0,1,…,N,j=0,1,…,N;
K表示车辆集合,K=1,2,…,k;
C表示车容量;
qi表示顾客的需求量;
dij表示顾客i到顾客j的距离。
定义如下决策变量:

零售商向顾客供货的VRP 模型表示如下:
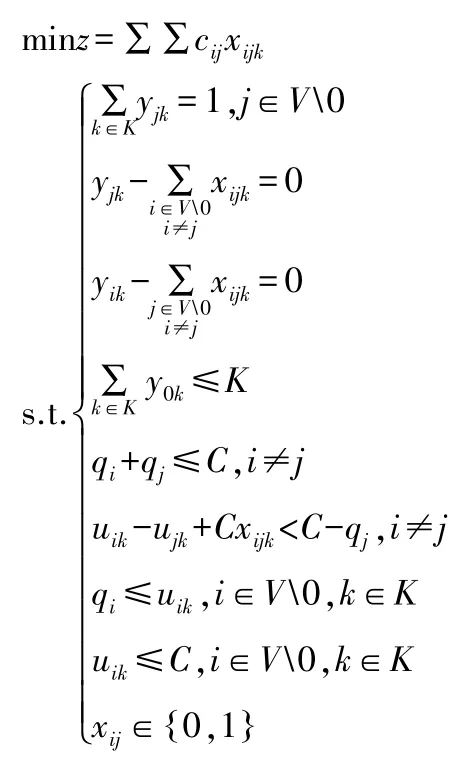
目标函数表示极小化运输成本,前三个约束保证了每位顾客只由一辆车配送,第四个约束表示使用的车辆数不超过给定的车辆数,第五个约束保证了不超过车辆容量,第六到第八个约束避免形成环路,xij为决策变量。
(二)合作博弈的超可加性
超可加博弈指的是任意两个不相交的联盟中的所有局中人组成一个更大的联盟时,他们所创造的利润不小于这两个联盟各自的利润之和,即对于局中人所组成的任意两个联盟S和T,若S∩T=∅,则必有:

若博弈为超可加的,那么大联盟就有可能形成,能够进一步增加利润。 在计算关于成本分摊博弈时,需要在式子两边同时添加负号,验证博弈是否为次可加的,次可加博弈的实质是形成大联盟后总成本更少。
(三)合作博弈解方案
大联盟形成后的成本分配方案可能有无限个,在个体理性的情况下,联盟中的每位零售商都想得到最有利的分配结果,一旦分配不公平,部分零售商就有可能退出大联盟,这种合作不一定能长久持续下去。 因此,要使大联盟稳定,必须保证不存在任何一个子联盟优于大联盟。
1. 核解
在合作博弈中,每个局中人i都有一个对应的分配成本xi,每个局中人分配的成本之和应等于大联盟N的总成本v(N)(即有效性),同时xi又不能劣于其他分配方案(即个人理性),这样博弈的核(Core)就可以定义为:

虽然一般情况下,核的内部有多种解方案,但核也可能为空,因此需要注意博弈是否有非空核。
2. Shapley 值
Shapley 值最早是由罗伊德·夏普利(Lloyd Shapley)在1953 年提出的,该利益分配方法在各个领域都有重要的影响。 Shapley 值是满足有效性、可加性、策略等价的相对不变性、虚拟局中人性和匿名性的单点解,其根据局中人的贡献来进行利益(或成本)的分配,它的具体形式如下:
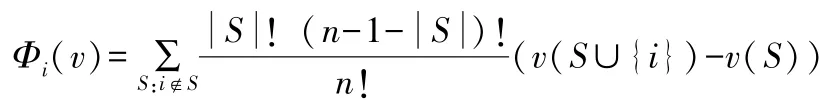
3. 核仁
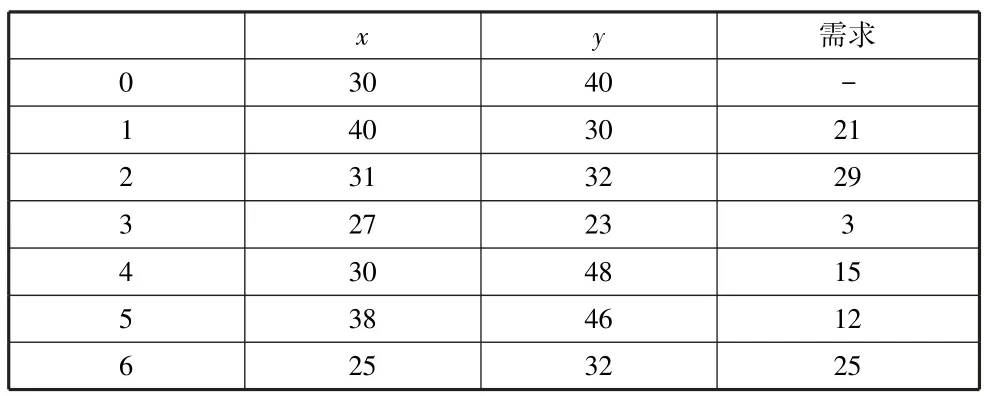
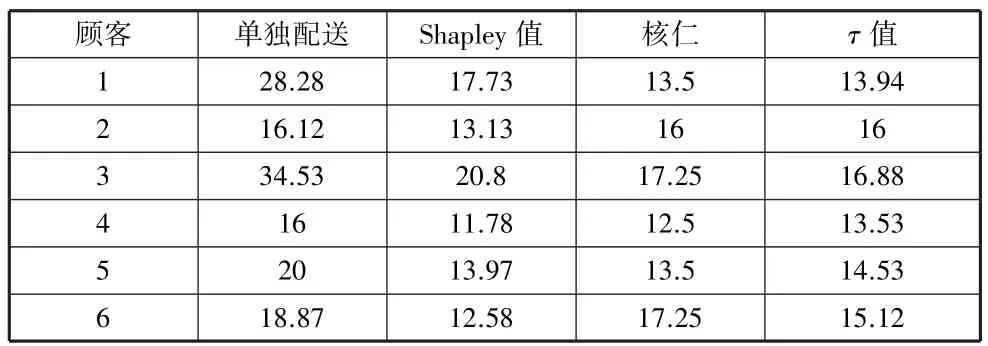
定义核仁,首先要定义联盟S关于x的超额θ(x,S),其中用来衡量联盟S对于该分配的不满意程度,可见,θ(x,S)越小,联盟S的满意程度越高。 在计算核仁的过程中,需要将θ(x,S)按字典序方式排序,即若k 4.τ值 τ值也是合作博弈中的单点解,我们首先定义上向量M(N,v)和下向量m(v)。M(N,v)是局中人的边际贡献,联盟S中局中人i的边际贡献就可以表示为Mi(S,v)=v(S)-v(S\{i})。 定义Pσ(i)为在排列σ里排在局中人i之前的局中人集合,Pσ(i)= {r∈N|σ-1(r)<σ-1(i)},局中人i在排列σ中下向量就可以表示为τ值就可以定义为: τ(v)=αm(v)+(1-α)M(N,v) 文章给出的算例中零售商是唯一的,6 个顾客分散在零售商周围,零售商与顾客坐标、顾客需求如表1 所示,数字0表示零售商,数字1 到6 表示顾客,车容量C=50 单位,单位运输成本为1。 表1 零售商与顾客坐标 本文采用MATLAB 软件进行编程及求解,版本为2015b。由于系统中有6 个顾客,则联盟总数共有26个,我们定义空联盟的特征函数为c(∅)=0,即空联盟的成本为0,根据第三节建立的VRP 模型,通过MATLAB 求解最优路径以及63 个子联盟的成本。 计算结果显示,当零售商单独向6 位顾客递送货物时的总运输成本为133.8,当使用 VRP 模型进行共同配送时,总成本为89.93,成本降低了43.87,说明共同配送确实能够有效减少物流成本,具体送货路径如图1 所示,各条路径的具体线路及成本见表2。 表2 具体路线及成本 图1 具体递送路径 根据图1,由于顾客2 距离零售商最近,且需求量大,因此由零售商单独配送;顾客4 和5 距离较近且总需求量没有超过车容量,因此零售商对其一起送货,顾客1、3、6 形成了一条配送路线。 在确定了最优配送路径后,我们计算所有可能的联盟的运输成本,并将63 个子联盟的成本作为博弈的特征值进行成本分摊。 计算结果如表3 所示: 表3 子联盟成本 通过根据上述博弈的特征值,计算Shapley 值、核仁和τ值,计算结果如表4 所示: 表4 成本分摊结果 图2 可以更直观地反映出进行共同配送时的成本下降程度,根据图2 可以看到每个顾客的成本都有所减少。 由于Shapley 值对成本的分配是根据每个顾客对大联盟贡献的多少来确定的,虽然顾客2 自己形成了一条路径,但是Shapley值认为顾客2 对大联盟也是有贡献的,所以顾客2 的成本也有一定减少,而顾客2 成本的减少势必会带来其他顾客成本的增加。 图2 成本分摊结果对比 核仁的计算原则遵循的是最大化最小超额,也就是找到让最不满意的联盟相对满意的唯一解。 根据核仁的计算结果可以看到,由于顾客2 自己形成了一条线路,它的成本和其单独配送时的成本相差不大,相比于Shapley 值,顾客1、顾客3 和顾客5 的成本有所下降。 τ值的分配方案与核仁相近,顾客2 的成本同样是16,顾客3 和顾客6 的成本较核仁分配方案有所下降。 当特征值满足次可加性时,大联盟才可能形成;核解是满足个人理性、集体理性和有效性的解,当分配方案属于核解时,该联盟更稳定,因此,接下来利用MatTuGames 工具箱验证博弈的次可加性以及Shapley 值、核仁和τ值是否在核中。 通过计算,结果显示该博弈满足次可加性,说明大联盟有形成的可能;但是经过计算,Shapley 值与τ值并不在核中,说明这两种分配方案不满足集体理性,即Shapley 值与τ值的成本分摊结果不能使联盟的合作可持续;而核仁的成本分摊结果在核解中,说明核仁解能够满足核解的一切性质,能够使所有参与合作的顾客都满意。 因此文章的成本分摊结果为顾客1 支付13.5,顾客2 支付16,顾客3 支付17.25,顾客4 支付 12.5,顾客 5 支付 13.5,顾客 6 支付 17.25。 文章考虑了单零售商多顾客的情况,以极小化运输成本(与距离有关)为目标,利用VRP 模型计算了实施共同配送时的总成本,相比于单独配送,合理的共同配送确实可以降低成本,提高货物的配送效率。 进一步的,文章考虑如何对总成本进行合理分摊,将所有子联盟的运输成本作为博弈的特征值,根据特征值进行了多种成本分配方案的计算,并将得出的结果进行了对比,结果显示进行合作时各个顾客的成本相比于单独配送时的成本均有所下降,但是Shapley 值与τ值的分配方案不属于核解,因此若实施这两种分配方案将会使合作失败,而核仁的分配方案在核中,因此这种分配方式能够使联盟稳定,使合作可持续。四、 算例分析




五、 结束语

