深水多梯度钻井井筒温度场

杨宏伟, 李 军, 柳贡慧,2, 高 旭, 王江帅, 骆奎栋

(1.中国石油大学(北京)石油工程学院,北京 102249; 2.北京工业大学,北京 100124;3.中国石油长庆油田分公司第二采气厂,陕西榆林 719000)

随着油气开发逐渐向深水领域进展,深水钻井中面临的问题也越来越突出,如窄安全密度窗口[1]、复杂的井身结构[2]、水合物堵塞井筒[3]等。多梯度钻井是一种解决上述问题的有效手段,该技术由Maurer等[4]于2003年提出。准确预测多梯度钻井中的井筒温度对于井筒流体物性参数确定、井筒压力精确控制以及井壁稳定性分析具有重要意义。国内外学者对于井筒温度的预测已经进行了大量的研究。Raymond[5]建立了第一个数值传热模型预测直井循环过程中的井筒温度。基于该模型,后续学者对其进行了改进,并利用先进的优化算法简化了求解过程,增强了计算结果的稳定性。如Espinosa等[6]基于井筒和地层的热交换原理,建立了循环和停泵过程中的瞬态温度模型,并利用全隐式有限差分法对其进行了求解;Ziabakhsh等[7]建立了一个二维的瞬态传热模型,并评估了利用地热资源产生能量的可行性;高永海等[8]基于传热学基本理论,研究了循环及停止循环条件下的深水钻井井筒温度场;杨谋等[9-10]考虑了钻具组合和井身结构对井筒温度的影响,模拟了井筒流体循环和非循环条件下的井筒-地层的传热过程;李梦博等[11]基于数值传热模型研究了钻柱旋转和热源项对井筒温度的影响;宋洵成等[12-13]采用数值传热模型研究了深水钻井和关井过程中的井筒温度场;王江帅等[14]考虑岩屑对井筒流体性能的影响,建立了一个井筒与周围环境之间的拟稳态传热模型。综上分析可知,这些模型主要是针对不同工况下的单相流体传热,在多梯度钻井中并不适用。笔者基于传热和传质机制,建立一套深水多梯度钻井中的综合温度场模型,并利用有限体积法对该模型进行求解。此外,利用该模型对深水多梯度钻井过程中的井筒温度分布特征以及环空温度对不同参数的敏感性进行分析。

1 数学模型

1.1 瞬态传热模型

多梯度钻井过程中,含有空心球的钻井液由井口注入钻柱内,当钻柱内的混合流体流至旋流分离器时,空心球被分离进入环空。多梯度钻井中井筒流体的循环过程如图1所示。

为了建立数值模型来准确地评估井筒及周围环境的热行为,假设:海水和地层的热物性参数(密度、比热和导热系数)为常数[15];旋流分离器对空心球的分离效率可以控制;忽略空心球进入环空后的加速过程,除分离器处之外的井筒中空心球和钻井液均匀混合。

假设流体流过一个静止的控制体单元,以此建立钻柱和环空内流体同时发生传热与传质时的瞬态传热机制模型。

控制体单元内钻井液和空心球的质量守恒方程分别为

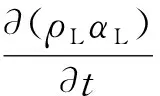
(1)

(2)

式中,ρ为密度,kg/m3;α为体积分数;v为流速,m/s;qs为空心球由钻柱向环空传递的质量流量,kg/(s·m2);t为时间,s;下标L和s分别表示钻井液和空心球。

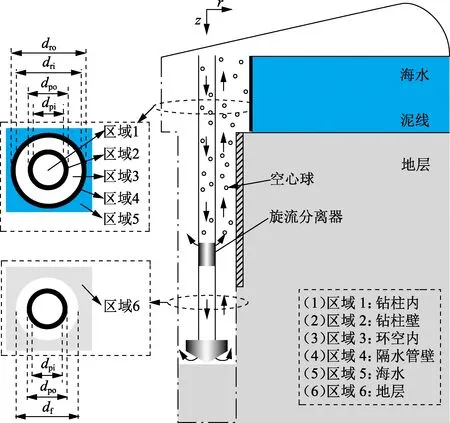
图1 多梯度钻井中井筒流体循环过程示意图Fig.1 Schematic diagram of wellbore fluid circulation in multi-gradient drilling

控制体单元内钻井液和空心球的动量守恒方程可表示为

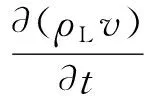
ρLαLgsinθ,

(3)

ρsαsgsinθ.

(4)

式中,p为井筒压力,Pa;F为偏应力,Pa;g为自由落体加速度,m/s2;θ为井斜角,rad。

根据热力学第一定律,控制体单元内钻井液和空心球的混合能量守恒方程可表示为

i=L, s.

(5)

式中,U为内能,J/kg;H为焓,J/kg;Q为热传导项。

根据傅里叶定律,混合流体的热传导项[15]可以表示为

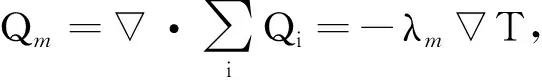
(6)

(7)

式中,λ为热导率,W/(m·℃);下标m表示混合流体。

根据控制单元体内内能、焓与温度的关系[16],将式(1)～(4)和(6)、(7)代入到式(5)中,得

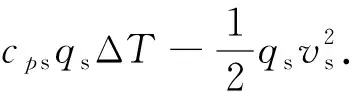
(8)

式中,cp为比定压热容,J/(kg·℃);T为温度,℃;ST为热源项。

式(8)即为考虑空心球传热和传质的通用三维瞬态传热模型。由于钻柱内和环空内的流动过程和传热机制不同,所以需要分别确定井筒流体在不同区域内的具体传热模型。

忽略井筒流体在径向上的温度变化,仅考虑其沿轴向的变化。柱坐标系统下钻柱内的瞬态传热模型为

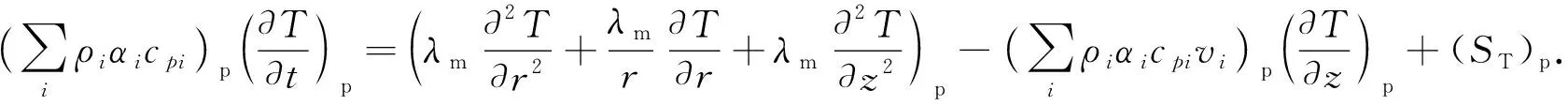
(9)

环空流体的瞬态传热模型为

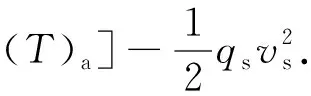
(10)

式中,下标p和a分别表示钻柱内和环空内的流体区域。

深水多梯度钻井中的热区域还包括钻柱壁、隔水管壁、套管壁、水泥环、地层和海水。根据能量守恒方程,固体区域的瞬态传热模型[17]为

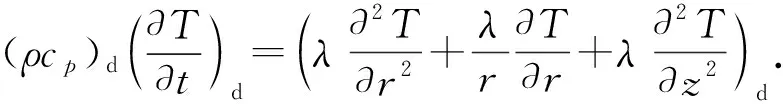
(11)

不考虑隔水管周围海水沿切向的温度变化,根据热力学第一定律,海水的瞬态传热模型为

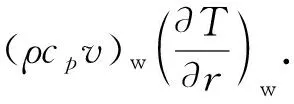
(12)

式中,下标d和w分别表示固体区域和海水区域。

1.2 初始和边界条件

井筒周围环境包括海水和地层区域。海水区域沿垂深的温度分布十分复杂,受多种因素影响,包括纬度、洋流、季节、深度等。不同深度下海水温度可以使用Levitus模型[18]表示为

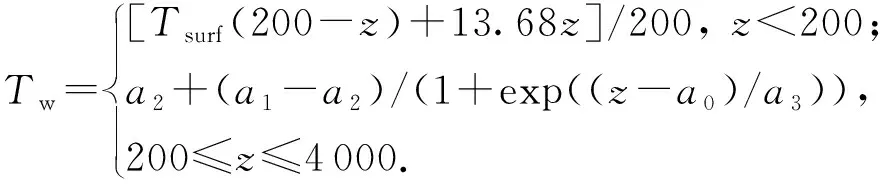
(13)

式中,a0=-130.137,a1=39.398 39,a2=2.307 13,a3=402.731 77;Tsurf为海水表面温度,℃;z为井深,m。

在泥线处,海水温度与地层温度相同,所以地层温度可以表示为

Tf=Twz=zml+Gf(z-zml)sinθ.

(14)

式中,Tf为地层温度,℃;Gf为地温梯度,℃/m;zml为泥线的深度,m。

在井筒-周围环境系统中各个热区域之间的传热过程中,流体区域与固体区域边界上的非稳态传热属于第三类边界条件,因此根据能量守恒原理,固液边界条件[17]可以表示为

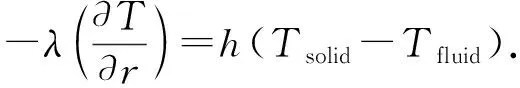
(15)

式中,Tsolid和Tfluid分别为固体壁和流体区域的温度,℃;h为对流换热系数,W/(m2·℃)。

1.3 对流换热系数

钻井过程中,钻柱内流体、环空流体以及海水的流动会引起流体区域和周围固体区域之间的强制对流换热。对流换热系数是关于努塞尔数、热导率和水力直径的方程,即

(16)

式中,Nu为努塞尔数;Dh为水力直径,m。

努塞尔数与流态和流动条件有关,在钻柱内、环空内和海水区域内不同。钻柱内层流和紊流条件下的努塞尔数Nu分别可以通过Petersen等[19]和Rao[20]的关系模型计算:

(17)

式中,Re为雷诺数;Pr为普朗特数;n为流性指数。

环空内考虑钻柱旋转条件下层流和紊流的努塞尔数Nu分别可以通过Sieder等[21]和Fénot等[22]的关系模型计算:

(18)

式中，Reeff为等效雷诺数;L为管柱长度,m;α和γ为系数,通常α=0.8,γ=0.3。

海水横向流过隔水管,努塞尔数Nu[23]可以表示为

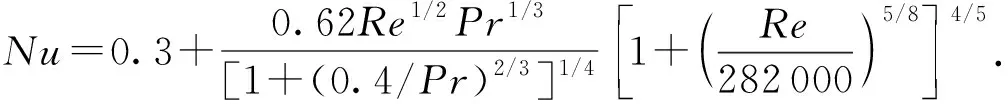
(19)

2 求解方法

井筒-周围环境系统中各个区域内的瞬态传热机制模型均为偏微分方程,因此可以采用有限体积法和全隐式差分格式数值求解整个循环过程中每个时间步长的系统温度[24]。

上述不同热区域内的瞬态传热方程可归纳为一个统一的形式:

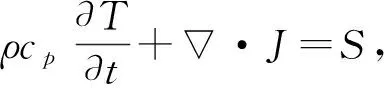
(20)

J=ρcpvT-λT.

(21)

式中,S为与时间和空间无关的项。

图2为有限体积法离散网格原理示意图。为了对方程进行离散和求解,将式(20)对控制体积和时间步长积分,可得:

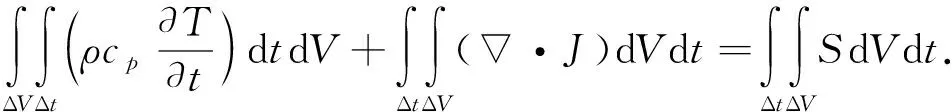
(22)

其中

使用全隐式数值离散格式对式(20)进行离散,可得:

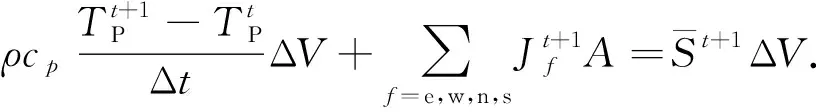
(23)

式(23)中的通量项包括热传导项和热对流项,将通量项展开,可得:

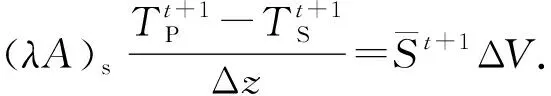
(24)

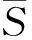
式(24)为瞬态传热模型的统一离散形式。每个热区域内的瞬态传热方程都可以根据其特征代入式(24),得到其最终不同的离散形式。离散后每个节点的方程可以整理成单广义向量的形式:

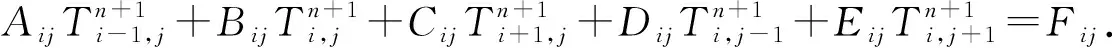
(25)

每个节点的离散方程的矩阵形式可以表示为

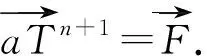
(26)

上述五对角线性方程组可以采用高斯-赛德尔迭代方法进行迭代求解,直到误差范围能够满足精度要求。详细的计算过程如图3所示。

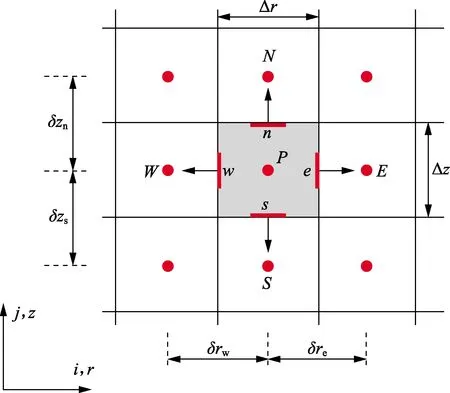
图2 有限体积法离散网格原理示意图Fig.2 Schematic diagram of discrete grid for finite volume method

图3 计算流程Fig.3 Flow chart of calculation process

3 模型验证

在环空流体的瞬态传热模型中,空心球引起的传热与传质项的物理意义明确。如果不考虑空心球的转移,上述模型同样适用于计算常规深水钻井中的井筒温度。因此在缺少多梯度钻井现场实测温度数据的条件下,可以采用常规钻井的现场实测温度数据对该模型进行验证。

X井是中国南海某区域的一口深水井。该井井深5 094 m,海水深度1 521 m;隔水管外径0.508 m,内径0.486 m;表层套管外径0.340 m,内径0.318 m,套管鞋位置深度2 860 m;中间技术套管外径0.244 m,内径0.224 m,套管鞋位置深度4 200 m;钻头直径0.216 m;钻杆外径0.127 m,内径0.111 m;钻井液密度1 200 kg/m3,塑性黏度34 mPa·s,排量0.024 m3/s;海水表面温度20 ℃,钻井液入口温度25 ℃,地温梯度0.024 ℃/m;钻井液热导率1.02 W/(m·K),定压比热容1 647 J/(kg·℃);其他热物性参数请见文献[15]。

当钻头由井深4 454 m钻至5 094 m的过程中,X井中MWD实测的环空温度与本文中模型计算的环空温度如图4所示。由图4可知,当计算温度不再受初始阶段的初始条件影响后,其与实测温度具有相同的变化趋势,而且随着钻进深度的增加,二者的吻合度越来越好。

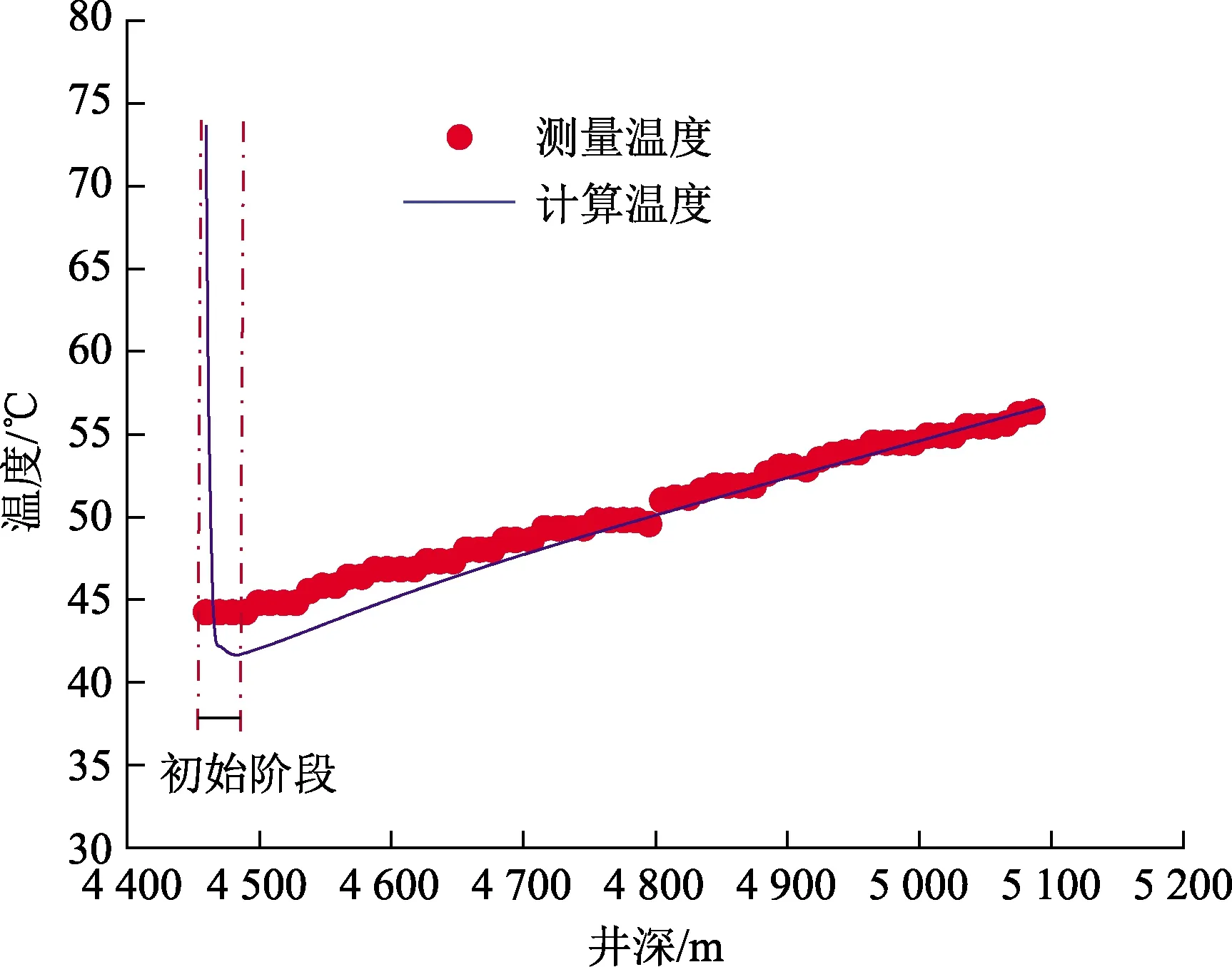
图4 X井的计算温度和测量温度Fig.4 Calculated temperature and measured temperature of well X

Y井是文献[25]中的一口深水井。该井井深1 744 m,海水深度1 152 m;海水作为循环流体,入口温度25 ℃;海水表面温度为25 ℃;井身结构参数请参见文献[25]。在该井的井底和出口处安置了温度测量仪,用来测量循环过程中的井底流体温度和出口流体温度。

图5为Y井循环过程中井底和出口流体的测量温度和基于本文中模型计算的温度随时间的变化。由于海水段和地层段的地温梯度相反,且地层段的井深较小,循环流体内部的热对流使井底温度先降低后逐渐升高,而出口温度逐渐降低。最终井底和出口温度都逐渐趋于稳定。总体而言,本文中模型的计算温度与测量温度的一致性较好,最大温度误差为2 ℃。因此利用本文模型来预测井筒温度可以满足工程要求。

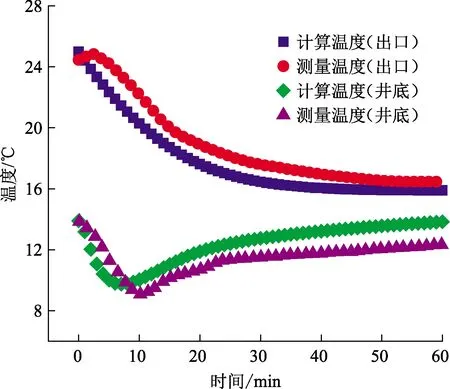
图5 Y井的计算温度和测量温度Fig.5 Calculated temperature and measured temperature of well Y

4 井筒温度变化特征

模型验证之后,仍然选择X井的基础参数进行模拟分析多梯度钻井中的井筒温度分布特征。多梯度钻井的基础参数:空心球密度为350 kg/m3,热导率为0.47 W/(m·K),定压比热容为750 J/(kg· ℃);分离器距钻头的距离为1 100 m;入口钻井液中的空心球质量分数为15%。

图6为不同时刻下环空温度剖面沿井深的变化。由图6可知,由于海水与地层的热物性参数差异较大,所以地层段各区域之间的传热速率要显著高于海水段各区域之间的传热速率,导致地层段环空温度趋于稳定的时间明显小于海水段。此外,空心球由钻柱进入环空的过程中伴随着传热与传质,导致旋流分离器处的环空温度沿流动方向突然降低,形成一个突变点。突变温度主要与空心球传递的质量流量和环空温度与钻柱内温度之差有关。随着时间的增加,环空温度与钻柱内温度之差逐渐减小,导致突变温度也逐渐减小。

图7为不同空心球质量分数条件下的环空温度剖面沿井深的变化。随着空心球质量分数的增加,旋流分离器之上的环空温度逐渐降低,尤其是在旋流分离器处。这主要是由于随着空心球质量分数的增加,环空流体的传热速率降低所致。在旋流分离器之下,环空温度变化不显著,且规律性较差,这主要归结于空心球的转移使该段的流体流速降低所致。流体流速降低导致对流换热系数和黏性耗散减小,但使热交换时间增加,所以该段环空温度的变化趋势要根据流体流速降低的范围确定。

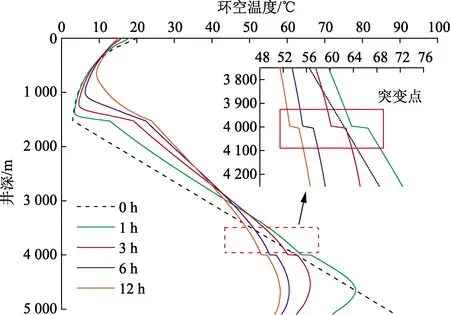
图6 不同时刻下环空温度剖面沿井深的变化Fig.6 Variation of annulus temperature along well depth at different times

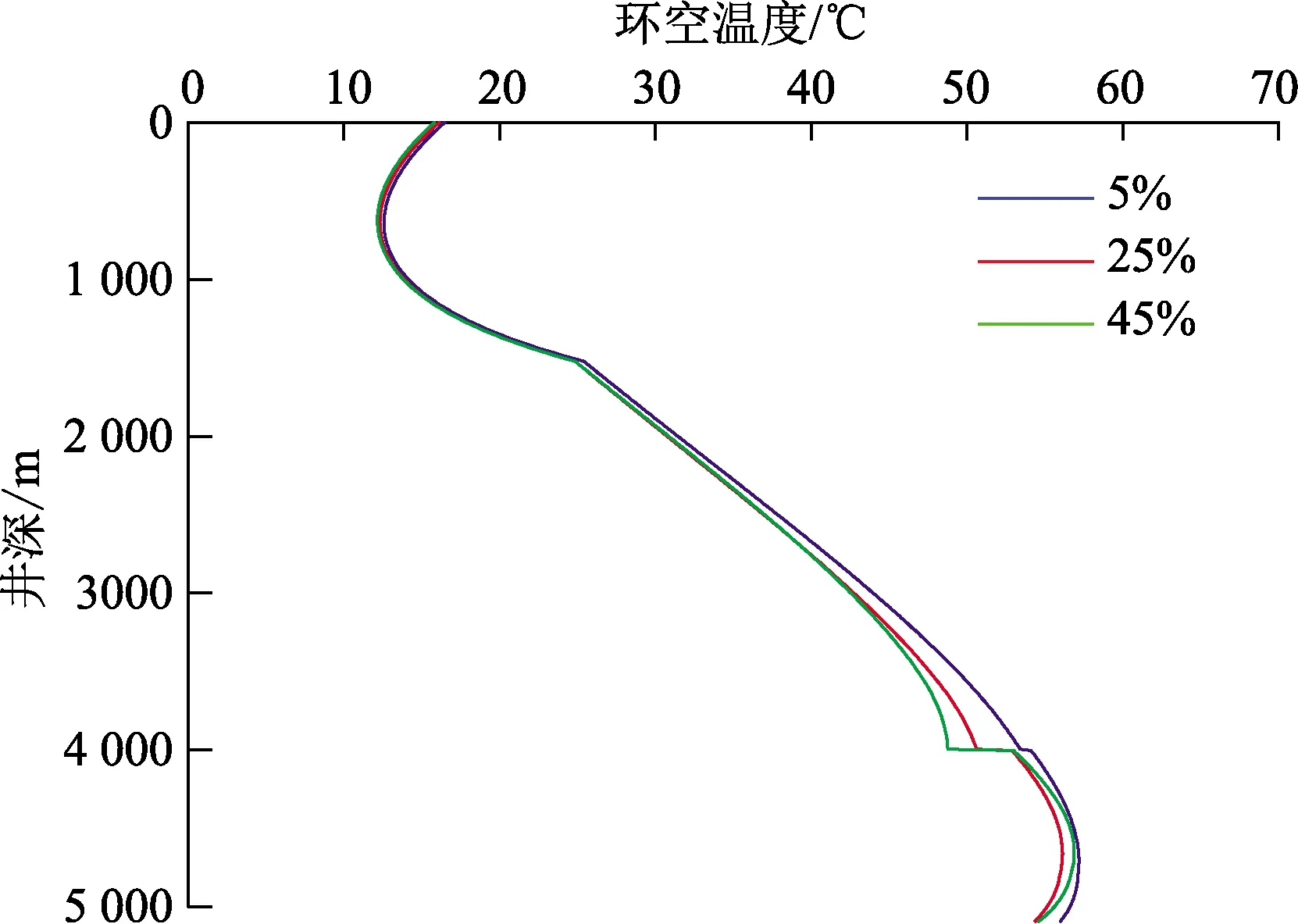
图7 不同空心球质量分数条件下环空温度剖面沿井深的变化Fig.7 Variation of annulus temperature profile along well depth under different hollow ball mass fraction conditions

图8为不同旋流分离器位置条件下的环空温度剖面沿井深的变化。分离器位置的改变使混合流体段和纯钻井液段的分布发生变化,环空流体与周围固体壁之间的热交换以及环空流体内部的热对流使环空温度随着旋流分离器距钻头的距离增加,旋流分离器之上的环空温度逐渐降低,而其之下纯钻井液段的环空温度逐渐升高。

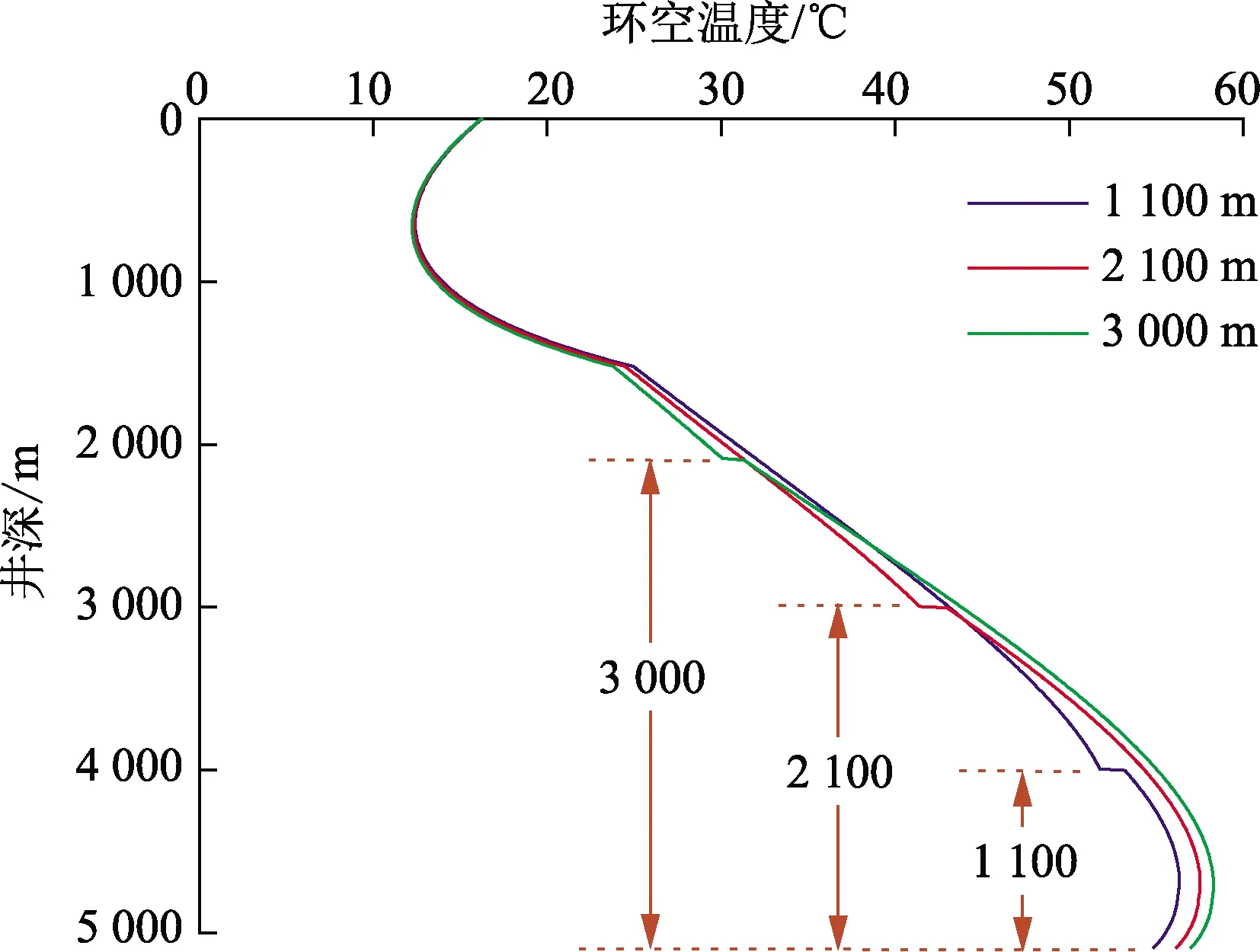
图8 不同旋流分离器位置条件下环空温度剖面沿井深的变化Fig.8 Variation of annulus temperature profile along well depth under different positions of cyclone separators

图9为不同旋流分离器数量条件下的环空温度剖面沿井深的变化。这里假设每个旋流分离器分离的空心球的量占初始空心球质量分数的1/n,n表示旋流分离器的数量。随着旋流分离器的数量自下而上的增加,井筒下部的环空温度逐渐增加,而井筒上部的环空温度变化规律性较差。这主要是由于旋流分离器数量对环空温度的影响是结合了空心球质量分数和分离器位置对环空温度的综合作用所导致的。但是对比图8和图9可知,环空温度对旋流分离器的位置更敏感。

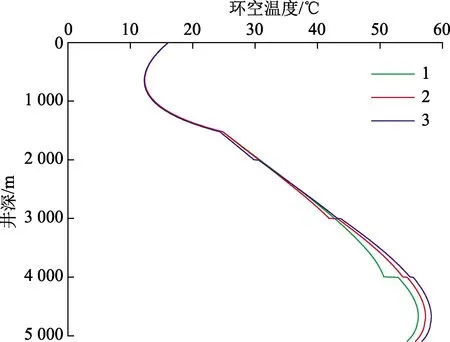
图9 不同旋流分离器数量条件下环空温度剖面沿井深的变化Fig.9 Variation of annulus temperature profile along well depth under different number of cyclone separators

5 结 论

(1)钻柱内的空心球经旋流分离器分离进入环空的过程中伴随着传热和传质,导致旋流分离器处的环空温度沿流动方向突然降低,形成一个突变点。

(2)空心球会使井筒流体的传热速率降低,导致随着空心球质量分数的增加,环空流体的温度逐渐减小,尤其是在旋流分离器处。

(3)旋流分离器的位置和数量的变化使空心球在井筒中的分布发生变化,从而改变环空温度。随着旋流分离器的数量和距钻头的距离的增加,下部环空温度逐渐升高,而上部环空温度变化较小。