单点系泊FPSO艏向角分析方法

张阳，刘波

（海洋石油工程股份有限公司， 天津 300451）

FPSO单点系泊系统与传统扩展式系泊系统的主要差别在于所系泊浮体是否具备风向标效应。风向标效应是指在受到风、浪、流联合作用时，FPSO可绕单点转塔旋转转向所受环境合力最小的位置。在实际环境条件下，由于FPSO单点系泊系统的风向标效应，FPSO艏向不断变化，并趋向于最小环境载荷位置，最终形成相对平衡[1,2]。

假设FPSO对地静止，此时环境波浪入射角及对应的波浪参数可用于FPSO的运动性能及结构强度校核。因此进行FPSO结构设计及运动性能分析，需要将全局坐标系下的环境波浪入射角及对应的波浪参数转化到FPSO局部坐标系[3,4]。鉴于传统扩展式系泊系统的特点，浮体艏向相对固定，全局坐标系中环境波浪入射角及波浪参数可直接用于局部坐标系进行设计分析，即环境波浪极值设计法。单点系泊FPSO由于其风向标特性，FPSO艏向不断变化，即FPSO局部坐标系下船体波浪入射角与整体坐标系下环境波浪入射角不一致。直接采用环境波浪极值设计法进行设计，会导致FPSO结构设计过于保守，提高FPSO建造成本；而FPSO运动性能失真，会提升FPSO设备、设施能力需求，最终增加FPSO总体造价。

本文研究的目的是通过艏向角分析解决风向标效应下，单点系泊FPSO船体波浪入射角求解难题，作为设计输入使FPSO的结构设计及运动性能评估更符合工程实际。

1 单点系泊FPSO艏向角分析理论

单点系泊FPSO平衡艏向求解是艏向角分析的核心内容。建立FPSO单点系泊分析模型后，对每个实际的环境工况，进行3h时域系泊分析，求解每一时间步长下，风、浪、流联合作用的FPSO转塔合力矩M。FPSO转塔合力矩M等于或趋近于0所对应时刻下的FPSO艏向角Ψ即为该环境工况下FPSO的平衡艏向。如在同一个环境工况下，存在多于合力矩M为0的时刻，则选取具有最大静态稳性的时刻下FPSO艏向角作为FPSO的平衡艏向。

图1 船体局部坐标系下环境入射方向定义

时域分析中单点系泊FPSO转塔合力矩M的计算公式：

其中：

Lt-船舯横剖面与单点转塔中心的最短水平距离，m；

Fwiy-FPSO Y轴上的风力分量，kN；

Fwdy-FPSO Y轴上的波浪漂移力分量，kN；

Fcy-FPSO Y轴上的流力分量，kN；

Mwiz-绕FPSO Z轴的风力矩，kN·m；

Mwdz-绕FPSO Z的波浪漂移力矩，kN·m；

Mcz-绕FPSO Z轴的流力矩，kN·m。

进行时域系泊分析时，流力矩应包含由FPSO风向标效应带来的艏摇低频粘性阻尼效应McψMolin/o。

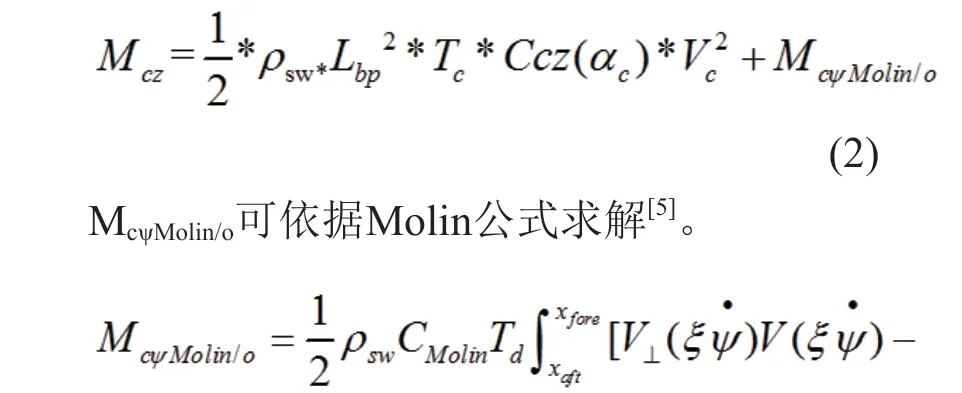
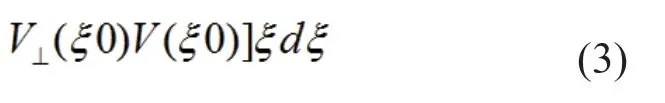
其中CMolin考虑力矩作用点的参数，以Ccy(90°)的百分比表征，可通过水池模型试验获取。

Xaft为FPSO坐标原点至FPSO艉垂线的距离，m；

Xfore为FPSO坐标原点至FPSO艏垂线的距离，m；

ψ为FPSO的艏向角，deg。

2 单点系泊FPSO艏向角分析方法

单点系泊FPSO艏向分析方法以获取实际海洋环境下船体波浪入射角为目的，求解过程主要分三步：

(1)确定单点系泊FPSO目标作业区的环境组合工况。环境数据覆盖的时间跨度越长，计算分析结果越准确，最好选取目标油田多年环境后报数据，如不具备相关数据也可考虑选用FPSO入级船级社建议的环境条件组合方式。

(2)时域系泊分析。以后报数据为例，对每个海况进行3h时域系泊分析计算，获得风、浪、流联合作用下，单点系泊FPSO平衡艏向。

(3)船体波浪入射角包络线。假设FPSO对地静止不动，将环境波浪入射角与单点系泊FPSO平衡艏向角组合，获得船体波浪入射角包络线。

3 计算示例

3.1 选取南海某油田环境后报数据

以目标油田的环境后报数据作为输入，构建后报数据数值模型，见图2至图4。

3.2 选取具有代表性的FPSO装载工况进行系泊分析

选取单点系泊FPSO操作具有代表性的中等装载吃水进行时域系泊分析计算[6,7]，得到实际海洋环境下FPSO平衡艏向，如图5所示。

图2 环境有义波高与环境波浪入射角的联合分布模型

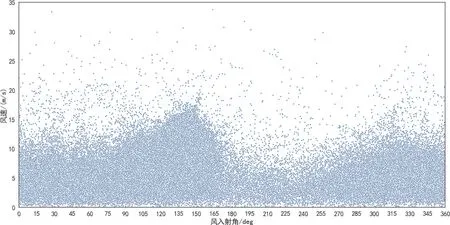
图3 环境风速与风入射角的联合分布模型

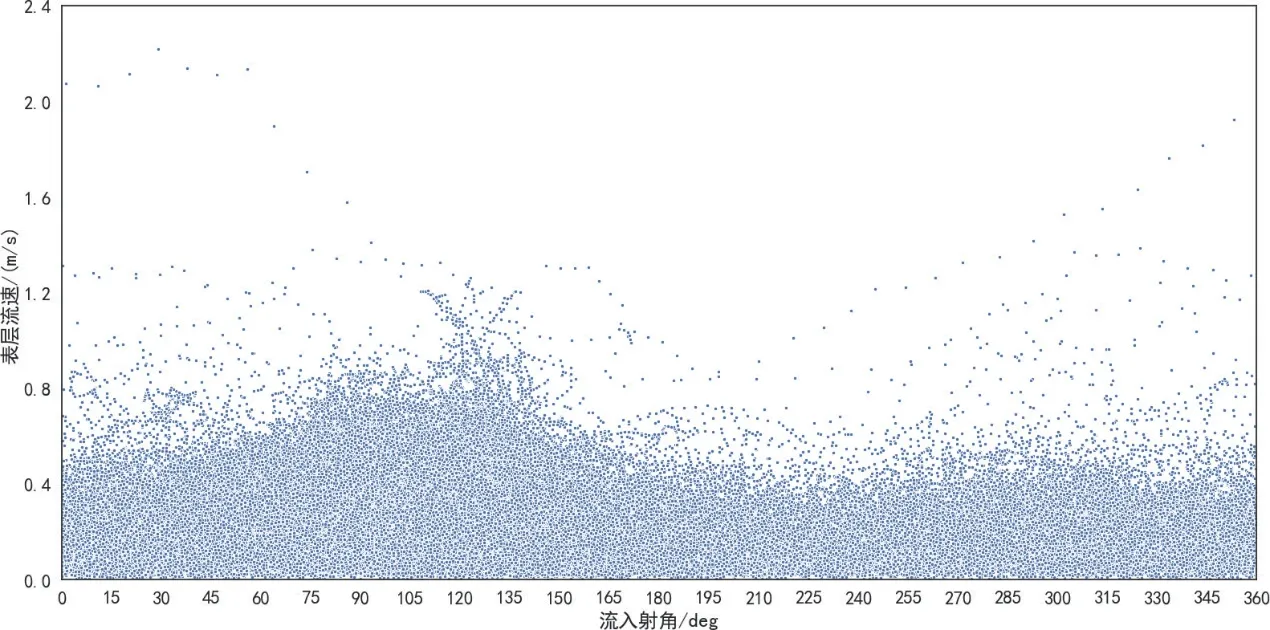
图4 环境流的表层流速与流入射角的联合分布模型

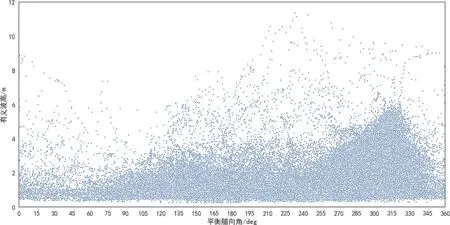
图5 环境有义波高与FPSO平衡艏向联合分布模型

3.3 艏向角分析包络线

将环境波浪入射角与单点系泊FPSO平衡艏向组合，统计船体波浪入射角包络线，并与环境波浪极值包络线进行对比，有义波高沿船体最高降幅达93.22%，如图6所示。

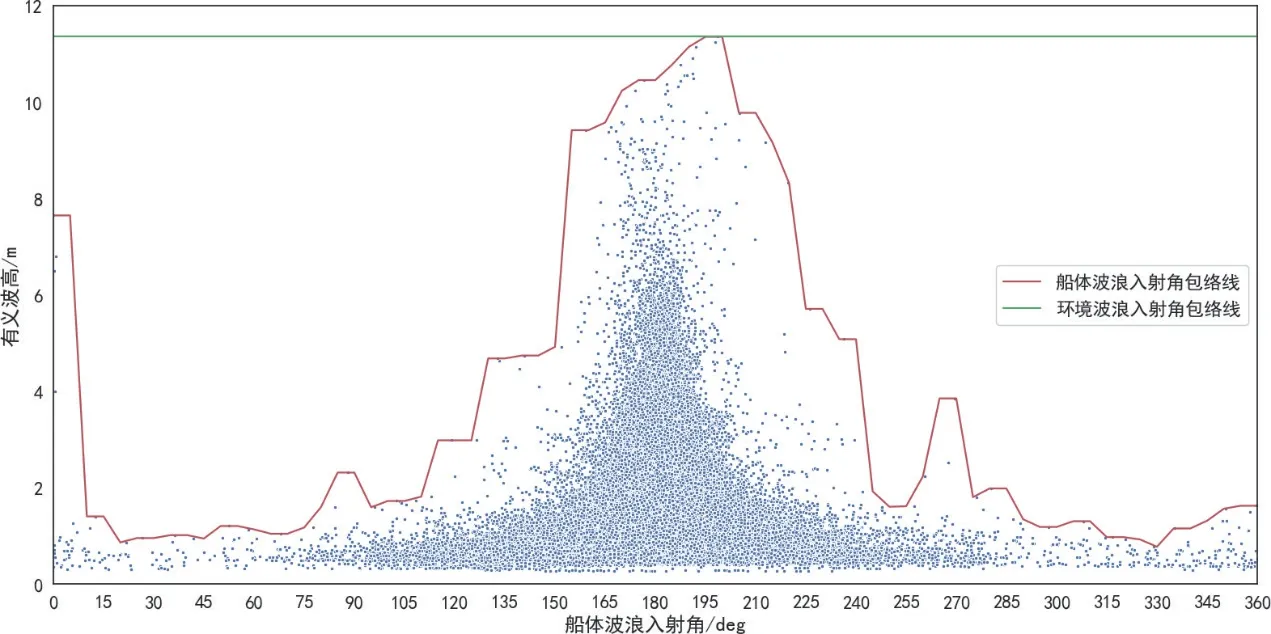
图6 船体波浪入射角包络线与环境波浪入射角包络线对比图

4 结语

对具备风向标效应的单点系泊FPSO应用单点系泊系统艏向角分析方法，相比环境波浪极值设计法，所得船体波浪入射角包络线，更符合工程实际，可有效降低FPSO的结构设计及运动性能评估的设计输入，现已应用于工程实际。

该方法不仅适用于单点系泊FPSO，还可拓展应用于渤海塔架式软钢臂单点FPSO设计，具有十分重要的现实意义。

◆参考文献

[1] 李达，白雪平，王文祥，等. 南海深水FPSO单点系泊系统设计关键技术研究[J].中国海上油气，2018，30(4)：196-202.

[2] 白雪平，李达，范模，等. 内转塔式单点系泊系统设计方法研究[J].海洋工程，2015，33(3)：36-42.

[3] 段雷杰，张少雄，杨洋. 基于设计波法的FPSO全船有限元分析[J].船海工程，2017，46(2)：48-53.

[4] 张海彬，赵耕贤. 水动力分析在海洋结构物设计中的应用[J].中国海洋平台，2008，23(1)：1-6.

[5] Molin B. Second-order Hydrodynamics applied to Moored Structures[M].British Maritime Technology.1994.

[6] 张阳，李卉. 不停产在位更换单点系锚泊系统的设计[J].石油和化工设备，2019，22(10)：67-70.

[7] 杨贵强. FPSO系泊系统设计相关因素分析[J].船海工程，2018，47(2)：123-126.