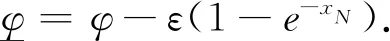一类各向异性椭圆问题的比较定理
朱秀丽
(东北电力大学理学院,吉林 吉林 132012)
考虑下列各向异性椭圆问题
(1)
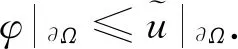
边界条件为

(2)
其中:Ω⊂RN是一个有界开区域,N≥2.
问题(1)-(2)源于在流体力学和假塑性流体的某些应用[1-4],并且受到很多学者的关注[5-9].在此类问题的研究中,比较定理使得我们可以用上下解的方法得到方程解的先验界[7-9],因此比较定理在解的存在性研究中起到非常重要的作用.
1 主要定理和证明
定理1设问题(1)-问题(2)中fi,i=1,2,…,N-1,g,P和f满足以下条件:
(A1)fi:[0,+∞)×Ω→[0,+∞),i=1,2,…,N-1,是连续函数,并且fi(·,x)(i=1,2,…,N-1)对于每一个x∈Ω为单增函数;
(A2)g:(0,+∞)×Ω→(0,+∞)是连续函数,并且g(·,x)对于每一个x∈Ω为单减函数;
(A3)K:[0,+∞)→[0,+∞)是连续函数;

(A5)f:(0,+∞)×Ω→(0,+∞)是连续函数,并且f(·,x)对于每一个x∈Ω为严格递减函数.
进一步假设:
(3)
φxixi≤0,i=1,2,…,N-1,
(4)
(5)
Φxixi≤0,i=1,2,…,N-1,
(6)

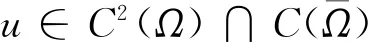

用公式(5)减去公式(1),得到

g(Φ,x0)K(|Φ|)-g(u,x0)K(|u|)=(g(Φ,x0)-g(u,x0))K(|u|)≥0.
由(A4)与(A5),有P(x0)(f(u,x0)-f(Φ,x0))<0.
从而


用公式(3)减去公式(1),得到
-g(u,x)K(|u|)≥P(x)(f(u,x)-f(φ,x)).
当x=x0时,经过类似的讨论,可以得到

2 主要定理的说明
1.条件(A1)、(A2)与(A5)可以分别用以下条件代替:
(B1)fi:R×Ω→[0,+∞),i=1,2,…,N-1,是连续函数,并且fi(·,x)(i=1,2,…,N-1)对于每一个x∈Ω为单增函数;
(B2)g:R×Ω→(0,+∞)是连续函数,并且g(·,x)对于每一个x∈Ω为单减函数;
(B3)f:R×Ω→(0,+∞)是连续函数,并且f(·,x)对于每一个x∈Ω为严格递减函数.

3.若公式(3)和公式(5)为严格不等式,则(A5)中f只需满足单减函数,不需要严格单调性,定理结论也成立.
4.考虑更一般的形式,如下
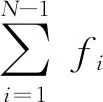
边界条件为(2).在(A1)中添加条件:对于任意u∈[0,+∞),x∈Ω,满足fi(u,·,x)∈C1(i=1,2,…,N-1).定理结论成立.
并且可以在uxNxN项前添加系数函数fN(u,u,x),fN的约束条件与fi(i=1,2,…,N-1)类似,并且添加条件φxNxN≤0和ΦxNxN≤0,此系统定理结论也成立.
5.如果方程不含有梯度项,即方程中g≡0,那么f约束条件不需要具有严格单调性.文献[7]讨论了2维情况,下面我们给出更一般的N维形式.
定理2设Ω⊂RN是一个有界开区域,
(7)
边界条件为
(8)

设fi,i=1,2,…,N-1,P分别满足(A1)和(A4),f满足以下条件:
(C)f:(0,+)×Ω→(0,+)是连续函数,并且f(·,x)对于每一个x∈Ω为单调减函数.
进一步假设:
(9)
φxixi≤0,i=1,2,…,N-1,
(10)


(11)
Φxixi≤0,i=1,2,…,N-1,
(12)

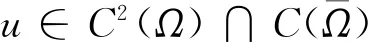
证明:不失一般性,假设xN≥0.