例谈模型构造法在解直角三角形中的应用

2020-10-26 10:14

（漳浦达志中学福建·漳州 363209）

模型构造法是分析实际问题中的数量关系，构造模型，转化为数学问题，利用相应的数学知识解决问题，它是一种有效的数学思考方法和解题策略。

1 锐角三角函数概念的理解是模型构造法的前提

锐角三角函数边的比值随角度的变化而变化，依托于直角三角形，不同的两边比值采用不同的符号。从勾股定理的掌握到锐角三角函数的概念的理解，全面地认识直角三角形，这是解直角三角形中模型构造法的前提。

例1：当梯子与地面所成的∠A满足50°≤∠A≤75°时，梯子可以安全攀登。现有一个把6m的梯子，问：（1）这个梯子最高可以安全攀上多高的墙?

（精确到 0.1m，sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）

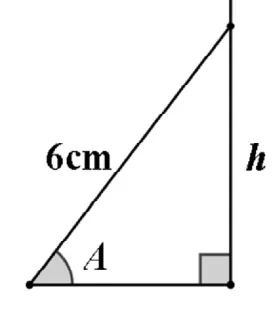
图1

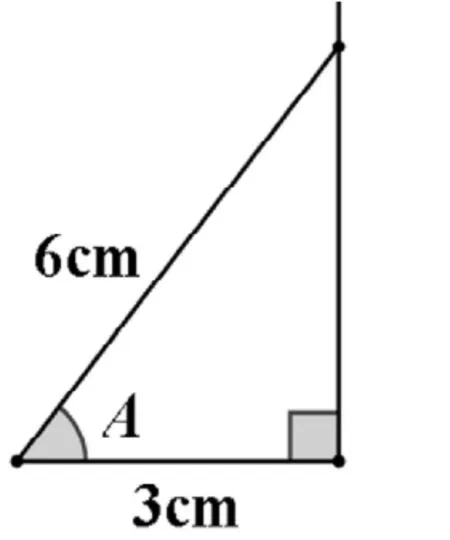
图2

（2）当梯子底端距离墙面3m时，梯子与地面所成的∠A等于多少？这时人是否能够安全使用这个梯子？

分析：从实际问题构造出基本模形，由斜边和∠A的取值范围，探讨梯子可以到达的高度范围，体现了直角三角形两边比值随角度变化而变化，蕴含了函数本质。正确理解锐角三角函数的概念有助于学生快速构造模型，利用模型解决问题。

不上高山，能测山高；不下湖泊，能测河宽。解直角三角形中测量问题种类较多，但模型构造主要为以下几类。

当观测点在被测物的异侧时，为异侧模型（背靠背型），解题策略为：作垂直，构造直角背靠背型，采用异侧求和法列方程解题。

例2：热气球的探测器显示，从热气球看一栋大楼顶部的仰角为30°，看大楼底部的俯角为60°，大楼高为，此时热气球与大楼的水平距离有多远？

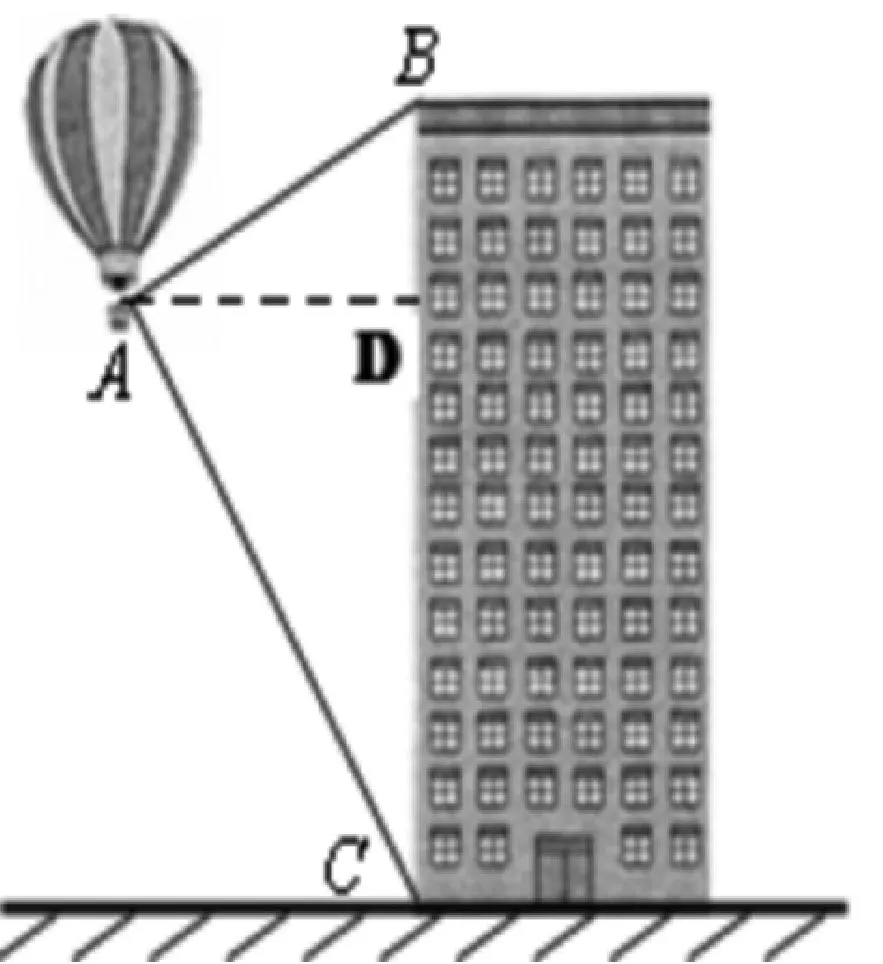
分析：本题被测物两端在观测点的异侧。解题策略：异侧模型，作垂直，构造直角背靠背型，采用异侧求和法解题。作垂线构造基本模型；以公共边设元是解决本题的关键，选择合适的关系式，构造方程解决问题。

当观测点在被测物的同侧时，为同侧模型（母抱子型），解题策略为：作垂直，构造直角母抱子型，采用同侧作差法列方程解题。

例3：某小岛P的周围海18里内有暗礁，一只小船由西向东航行，在点A测得小岛P在北偏东60°方向上，航行12海里到达B点，又测得小岛P在北偏东方向45°上。如果小船不改变航线继续向东航行，有没有触礁危险？请说明理由。

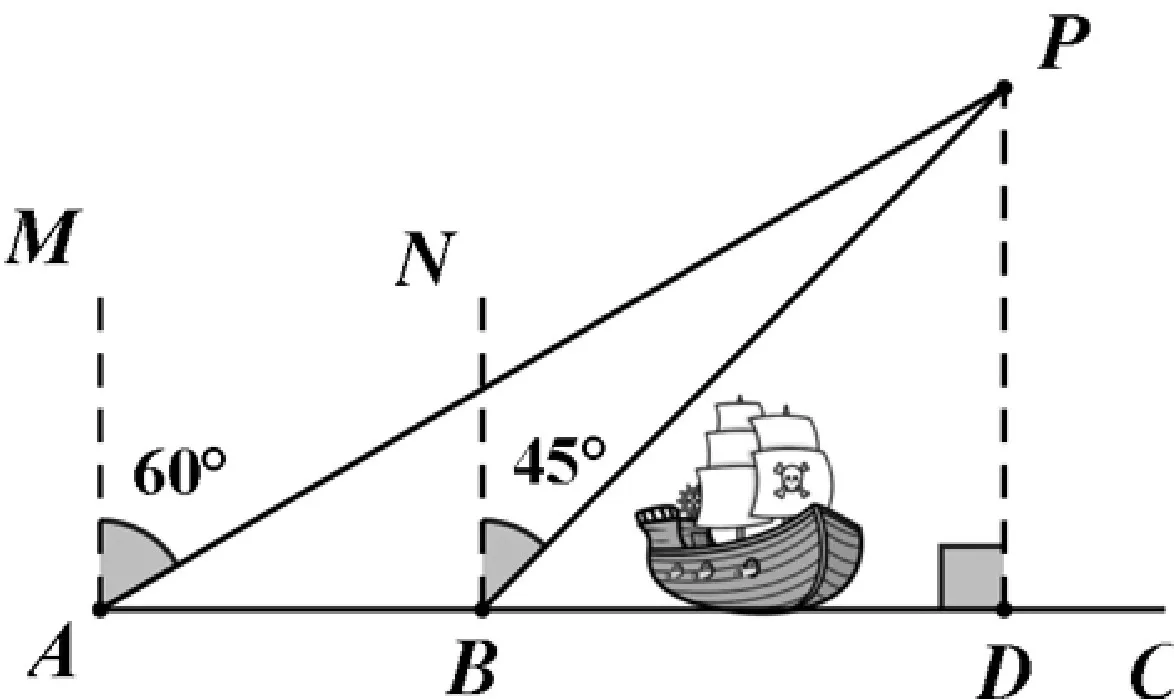
分析：本题被测物的两端在观测点的同侧。解题策略：同侧模型，作垂直，构造直角母抱子型，采用同侧作差法解题。作垂线构造基本模型；紧扣公共边是解题的关键。

当观测点较多且处于同一观测平面时，可结合实际构造同侧或异侧模型，化难为简。寻找不同平面的交集，即找到构成不同直角三角形的公共元素，如公共边或公共角，使不同平面的图形得以联系，此类题型多为中考的创新题。

例4：龙文塔是漳州古城的标志性建筑，巍峨秀丽，俯瞰西溪。学习小组在点A处测得龙文塔顶C的仰角为45°，塔底D的仰角为30°，前进20米到点B，此时测得塔顶C的仰角为60°，求龙文塔的高？

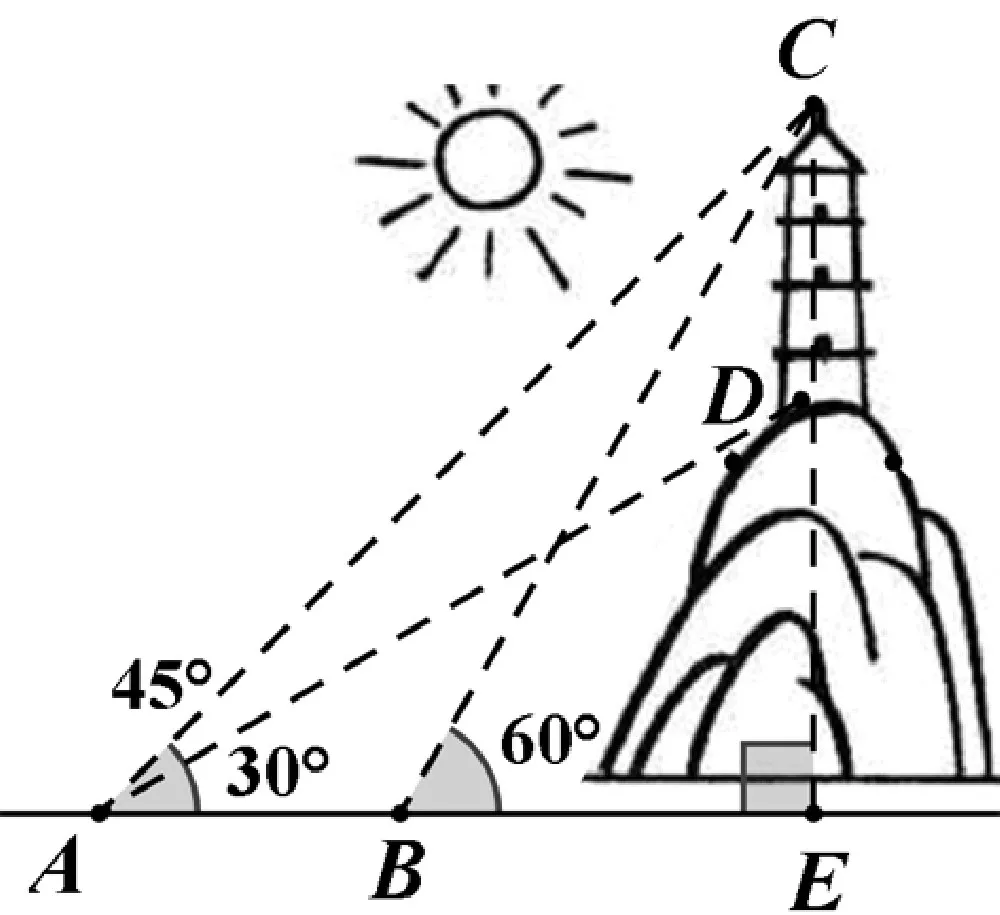
分析：本题有两处观测点，都在被测物两端的同侧，条件较多，图形较散，作出垂直，可使分散的条件联系在一起，解题策略：同侧母抱子，作差列方程，紧扣公共边设元，使分散的已知条件联系起来。

从不同的情境中抽象出合理的数学结构，转化为图形边角问题，用规范的符号语言表述，就能把复杂的问题简化，快速寻找到解决问题的方法和策略。

当有多个不同的观测点时，观测平面可能会有多个，这是多点测量模型（空间转换型），解题策略为：寻找不同平面的交集，即找到构成不同直角三角形的公共元素，如公共边或公共角，使不同平面的图形得以联系。

例5：小颖想测量河对岸树AB的高，在树底B的正对岸C 处，测得∠ACB=30°，河的两岸平行。（1）若河宽 BC=60米，求树AB的高；（2）若河宽BC的长度无法直接测量，她从点C出发，沿河岸前进20米到达点D处，测得∠BDC=60°，求树AB的高。

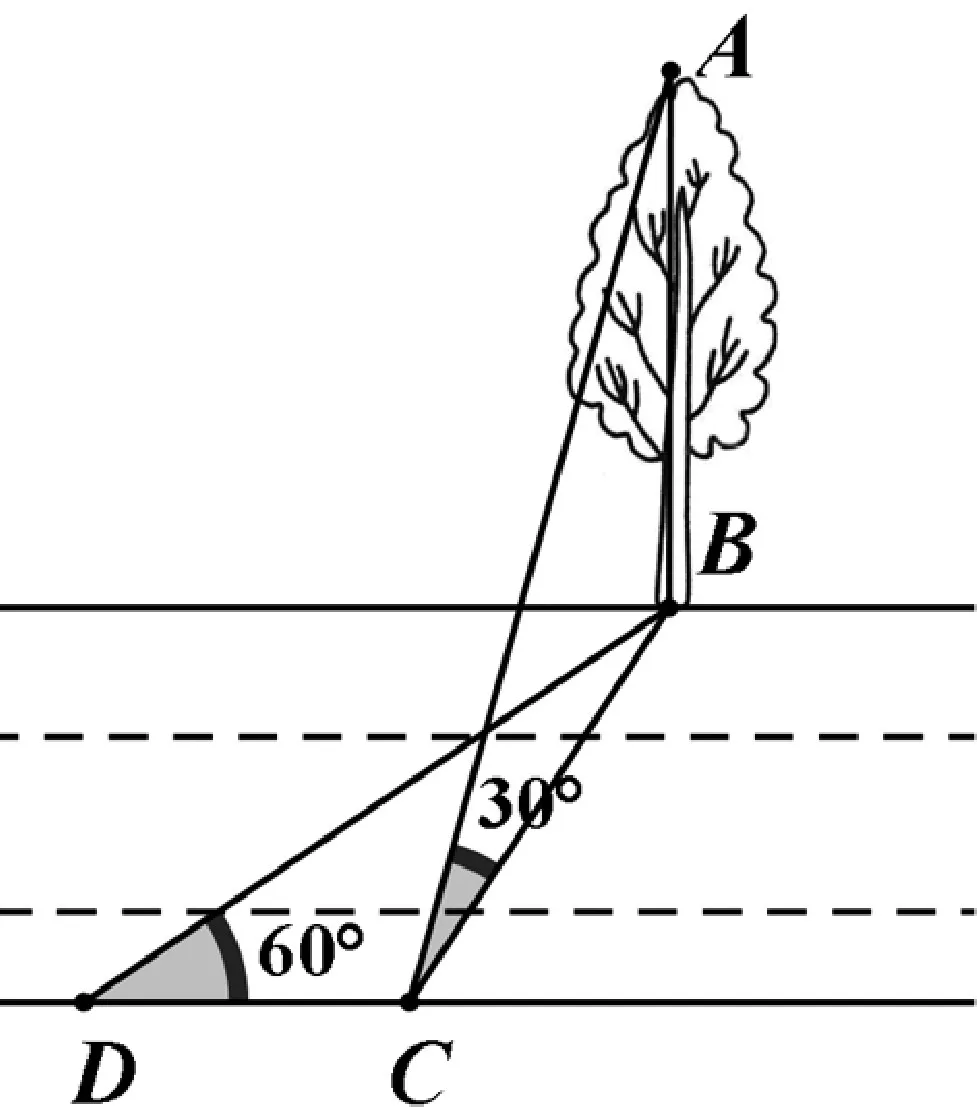
分析：本题的观测点有两处，在测量中形成了两个不同的平面，需要学生有一定的空间想象力，关键是抓住不同平面的交集，两个不同平面直角三角形的公共边，进行空间转换。

几何计算三法为勾股定理、锐角三角函数和运用相似比。数学解模要注重巧思细算，宁乘勿除是减少计算失误的有效方法。

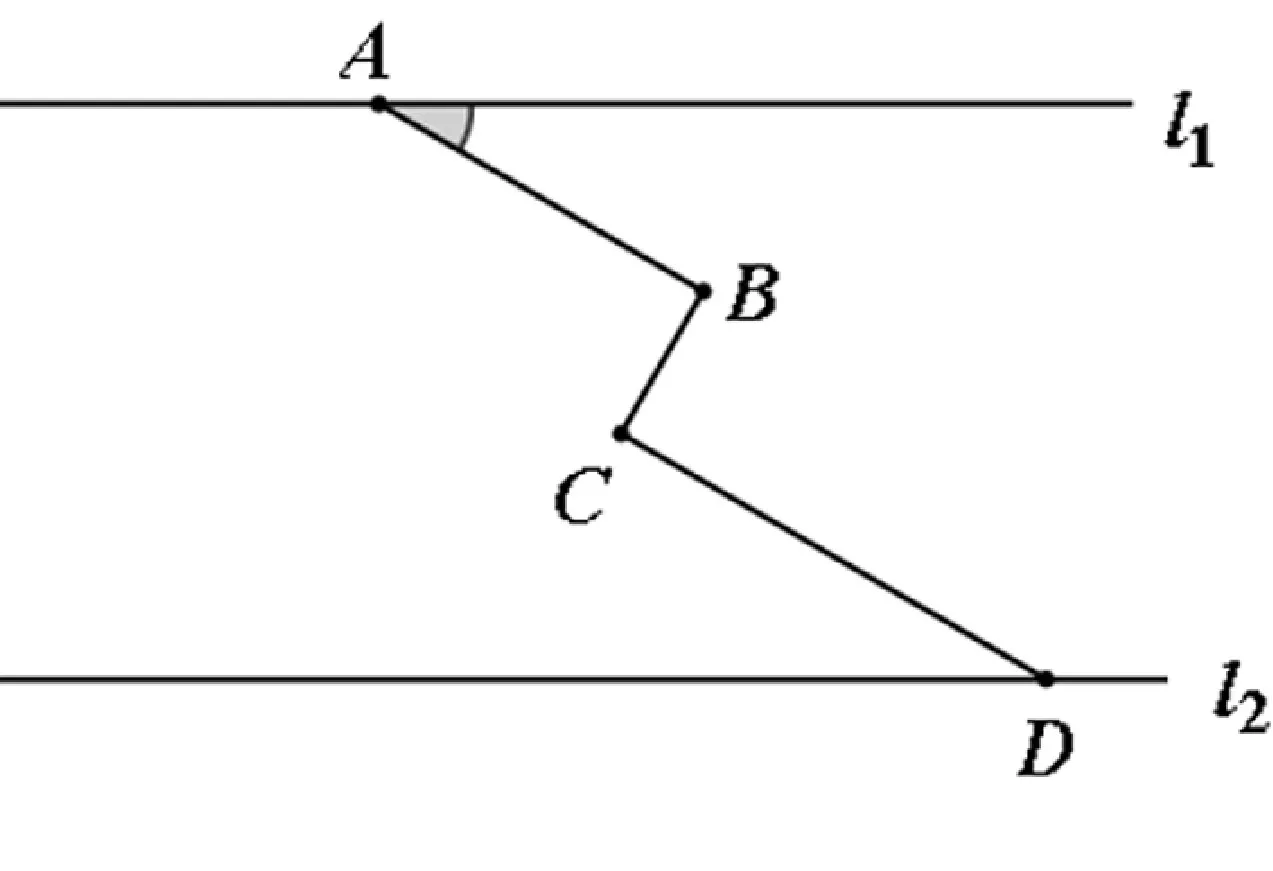
图3

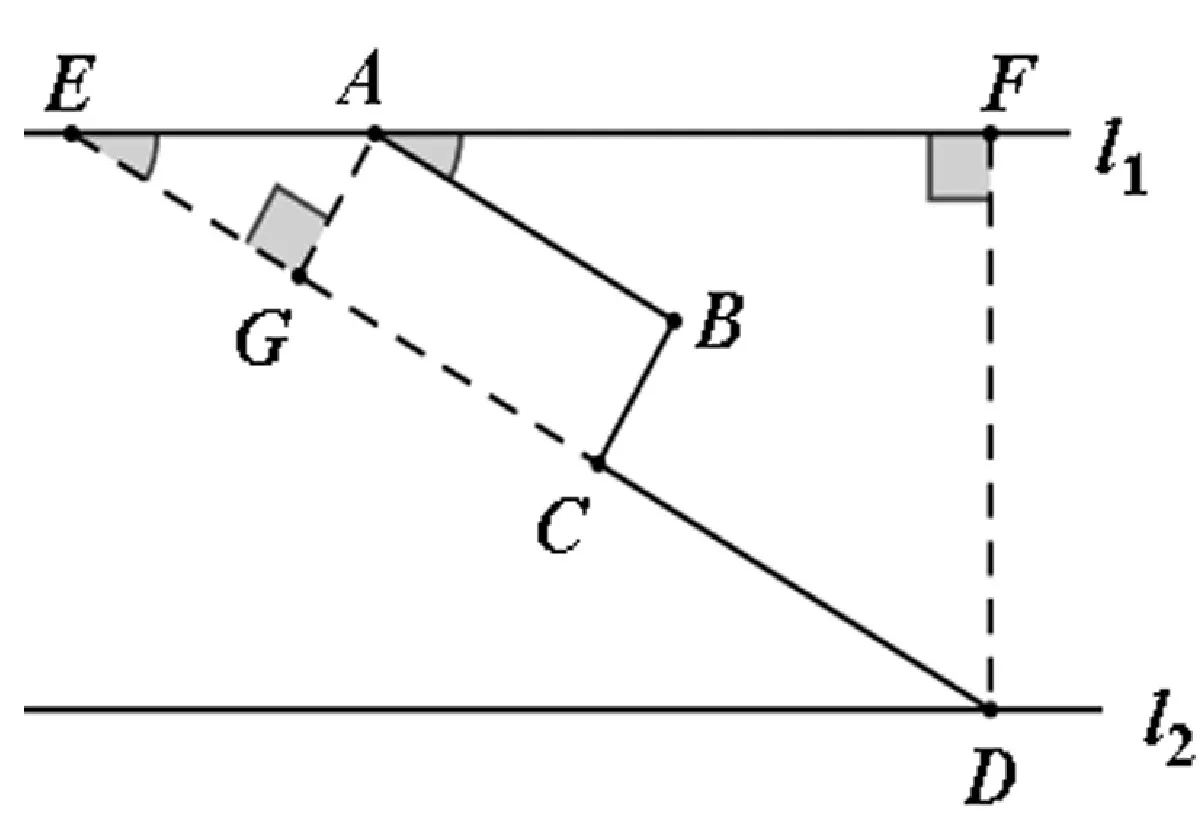
图4

分析：不同的直角三角形构造可以产生不同的解法，但各种解法计算的繁易程度不同。合造的构造，能使分散的已知条件集中，化折为直，使计算更简便，有利于更快解决问题。

解直角三角形的模型构造，蕴含多种数学思想方法。将实际问题抽象出数学问题，画出图形，使之转化为解直角三角形的计算、推理问题；从图形分析数量关系，以公共边设元（解题关键），用三角函数表述边角关系、列方程求解；解方程并检验解的合理性，从而使实际问题得到解决。