基于组合赋权法和未确知测度模型的发动机健康状况评估

韩亚娟, 杨玉琪

(上海大学 管理学院，上海 200444)

0 引言

发动机是飞机的“心脏”，其健康状况直接决定了飞机的安全性与可靠性。据美国空军材料实验室统计，1963～1975年间，美国空军战斗机共发生飞行事故3824起，其中由发动机故障引起的事故有1664起，占总数的43.5%[1]。据中国航空工业部质量司统计，1952～1983年间，在中国空军发生的战机等级事故中由发动机引起的事故占48.3%；而在其中的一等事故中，由发动机引起的事故约占38%[2]。2003～2013年间，我国民航事故中由机械和机务原因引起的占25%，在这些机械和机务原因中，发动机故障所占比例则高达60%[3]。由此可见，发动机的安全问题已成为航空业普遍存在且突出的问题。对航空发动机进行健康状况评估，能为后期有区别地、有针对性地对不同发动机制定不同的维修、更换或报废的管理决策提供依据，对降低发动机的故障发生率，提高飞机的安全性具有重要意义。

目前，关于飞机健康状况评估的方法有很多，如灰色聚类法、模糊综合评判法、人工神经网络法和支持向量机等。崔建国等提出了基于模糊灰色聚类和组合赋权法的飞机健康状况评估方法，将健康状况分为5个等级，利用模糊灰色聚类得到飞机健康状况等级隶属度，根据隶属度最大原则确定飞机的健康等级[4]。Lv等利用多层次灰色综合评价方法，按照5分制规则，自下向上得到控制系统的质量评分，以此确定控制系统的健康水平[5]。陈俊洵等采用经验模态分解和奇异值分解提取特征变量，并运用马田系统对特征变量进行筛选，最后基于马氏距离得到滚动轴承的健康指数[6]。丰世林等针对民航飞机健康状况评估过程的模糊性和不确定性问题，构建了基于层次分析法和T-S模糊神经网络相结合的评估方法对飞机的健康状况进行评估[7]。Diez-Olivan等利用支持向量机对柴油机进行健康状况评估，由柴油机子系统到超平面距离的对数标准化值得到子系统的健康评分，结合子系统的权重，最终得到柴油机的健康评分[8]。上述评估方法在确定评价指标权重方面或是只考虑了主观与客观赋权法中的一种，或是主客观组合赋权法的可解释性较弱。另一方面，上述评估方法得到的评估结果，一种是健康等级，不同等级的评价对象之间健康状况得以区分，但是相同等级不同评价对象之间却无法进一步区分；另一种是健康评分，不同对象的评分不同，因而所有对象间可相互区分，但是得到的健康评分因为在数值上相差不大，因而评价对象的区分度不是很高。基于此，本文拟采用一种基于组合赋权法和未确知测度模型的评估方法，从指标赋权和评价模型两个方面，实现对发动机健康状况的有效评估和区分。

1 基于逼近理想点的组合赋权法

1.1 赋权方法的选择

指标权重是一个评估系统的重要组成部分，是指评价指标对整个评估系统的重要程度或价值高低，对评价指标合理赋权关系到最终评估结果的准确性。现有的赋权方法可分为主观赋权法、客观赋权法和组合赋权法三种。常用的主观赋权法有德尔菲法、层次分析法、序关系分析法(G1法)[9]、专家排序法等。主观赋权法根据专家自身的经验和知识对评价指标进行重要性排序和主观赋权，体现的是专家对评价指标重要性的主观意愿，得到的权重可解释性较强。然而，主观权重并不能体现评价指标的数据信息。客观赋权法可分为三类：(1)基于指标间相关关系的客观赋权法，如复相关系数法[10]；(2)基于指标值提高难度的客观赋权法，如指标难度赋权法[11]；(3)基于指标差异程度的客观赋权法，如熵权法、变异系数法、双基点法(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)[12]、基尼系数赋权法[13]等。客观权重反映了评价指标的数据信息，然而其会随着评价对象集的变化而变化，即稳定性要弱于主观权重；同时，客观权重无法体现评价指标自身的重要性，且解释性弱于主观权重。

基于主客观赋权法各自的优点与不足，很多学者开始对组合赋权法进行研究，希望通过组合赋权，既保留主客观赋权法的优点，又克服主客观赋权法的不足。现有的组合赋权法包括乘法合成法[14,15]和加法合成法[16～19]。乘法合成法会引起“倍增效应”，且当评价指标个数较少时，这种“倍增效应”尤为突出。因此，乘法合成法一般适合指标个数较多，指标权重分配较均匀的场合，应用范围有限。加法合成法相对来说应用更广，研究也更多，其关键是确定指标的权重系数。崔建国等在对飞机液压系统进行健康状况评估时，直接给出评价指标的权重系数，并没有对其进行解释[4]。王明涛根据主客观权重的排序，将评价指标权重系数的确定分为5种情况，组合权重的最终结果或是主观权重或是客观权重或是主客观的平均组合权重[16]。该方法虽然考虑了指标组合权重与重要性一致的问题，但是指标权重系数的确定不够灵活，且未考虑评价对象的区分度。沈阳武等基于矩估计理论以组合权重与主客观权重偏差最小为目标函数，构建规划模型得到指标组合权重[17]。该方法得到的组合权重最大程度地发挥了主客观权重的优点，但其既没有考虑评价对象的区分度，也忽视了指标组合权重与重要性的一致性问题。迟国泰等以非违约企业的数据到正理想点的距离与以违约企业的数据到负理想点的距离的代数和最小为目标函数，构建规划模型得到指标组合权重[18]；孙莹等以所有指标对所有评价对象的总方差最大为目标函数，构建规划模型得到指标组合权重[19]。这两种组合赋权法，前者增加的是不同类别的评价对象之间的区分度，后者增加的是所有评价对象之间的区分度，两者均未考虑指标组合权重与重要性的一致性问题。

本文拟采用基于逼近理想点的加法合成组合赋权方法，首先利用G1法、指标相关性赋权(Criteria Importance Though Intercrieria Correlation，CRITIC)法和指标难度赋权法求得评价指标的单一权重，然后在指标权重与指标重要性一致的前提下，以正常评价对象到正理想点的距离和以异常评价对象到负理想点的距离之和最小为目标函数，建立规划模型，求得主客观权重系数，最后得到评价指标的组合权重。该组合赋权法既能反映专家的主观经验，又能反映数据的客观信息；同时消除了组合赋权方法中指标权重可能与指标重要性相悖的弊端，使组合权重更加科学合理；而且，可提高不同类别的评价对象的区分度。

1.2 G1法

G1法是由郭亚军教授提出的一种主观赋权方法[20]。该方法通过在指标间建立序关系确定指标重要性的大小关系，从而得到指标的主观权重。其具体步骤如下：

(1)根据专家经验确定评价指标的序关系

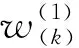
(2)确定相邻指标间相对重要程度的比值

设r(k)为指标x(k-1)与指标x(k)的相对重要程度的比值，表1为r(k)的赋值参考表。

(3)计算排序最末位指标的权重

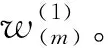
(1)

(4)逆序计算剩余指标的权重

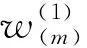
(2)

表1 r(k)的赋值参考表

1.3 CRITIC法

CRITIC法是由Diakoul提出的一种客观赋权法[21]，以“对比强度”和“冲突性”为基础计算指标权重。其中，对比强度是指同一个指标在不同评价对象之间取值差异的大小，用标准差来表示；冲突性通过指标之间的相关关系计算得到。其具体步骤如下：

(1)指标规范化

设有n个评价对象，m个评价指标，xij表示第i个评价对象第j个评价指标的原始数据，yij表示第i个评价对象第j个评价指标的规范化数据。

对于越大越优的指标，即效益型指标，规范化公式如下：

(3)

对于越小越优的指标，即成本型指标，规范化公式如下：

(4)

对于越接近某个目标值越优的指标，即固定型指标，规范化公式如下：

(5)

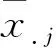
(6)

(2)利用规范化数据计算第j个指标的标准差σj，

(7)

(3)利用规范化数据计算第j个指标与第j′个指标的相关系数rjj′，

(8)

(4)计算第j个指标与所有指标之间的总冲突性fj，

(9)

(5)计算第j个指标包含的信息量cj，

cj=σjfj

(10)

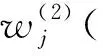
(11)

1.4 指标难度赋权法

指标难度赋权法以指标的提高难度为基础，提高难度用指标的极大值与均值的偏离程度来表示。一般来说，关键指标的提高难度相对较大。其具体步骤如下：

(1)计算第j个指标的极大值与均值的偏离程度zj，

(12)

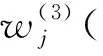
(13)

1.5 基于逼近理想点的组合赋权法

组合赋权法的基本原则是保证最终的权重与评价指标的重要性一致，目的是要将不同种类的评价对象最大程度地区分开。本文在遵守赋权的基本原则下，以正常评价对象规范化后的加权数据与正理想点的距离和以异常评价对象规范化后的加权数据与负理想点的距离之和最小为目标函数，建立规划模型，求解最优组合权重，以最大程度地对评价对象进行区分。

(1)正理想点与负理想点

正理想点是指评价对象各个指标加权后的规范化数据都达到最大值；负理想点即为评价对象各个指标加权后的规范化数据都达到最小值。

1)加权规范化后的数据

设第j个指标的组合权重为wj，由公式(3)～(5)可得到第i个评价对象第j个评价指标的规范化数据yij，则加权后的规范化数据sij为

sij=wjyij

(14)

2)确定正理想点

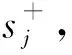
(15)

当评价对象状况最佳时，任何一个指标规范化后都达到最大值1，则正理想点S+可表示为

(16)

3)确定负理想点

(17)

当评价对象状况最差时，任何一个指标规范化后都达到最小值0，则负理想点S-可表示为

(18)

(2)规划模型的建立

1)评价对象的向量表示

将每个评价对象看成一个点，用各个评价指标加权后的规范化数据元素构成的向量来表示评价对象，则第i个评价对象Ei可表示为

Ei={si1,si2,…sim}={w1yi1,w2yi2,…,wmyim}

(19)

2)计算正常评价对象到正理想点的距离

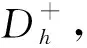
(20)

3)计算异常评价对象到负理想点的距离

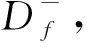
(21)

4)建立规划模型

(22)

s.t.w(k-1)≥w(k),k=m,m-1,…,2

(23)

θ1+θ2+θ3=1

(24)

θ1≥0,θ2≥0,θ3≥0

(25)

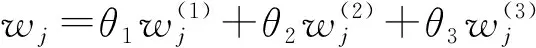
(26)

式(23)表示评价指标最终的组合权重需与指标的重要性保持一致，w(k)表示按照G1法重要性排序后，第k位指标的组合权重。

(3)确定指标组合权重

1)对规划模型进行求解，得到最优组合权重系数θ1、θ2和θ3。

2)根据式(26)，得到最优组合权重wj。

2 基于未确知测度健康状况评估模型的构建

未确知测度模型作为未确知数学的重要内容，其测度函数构造严谨，评价结果精细可靠。该模型通过将评价指标分成若干等级，建立测度函数，得到各个评价指标属于不同等级的未确知测度；结合指标权重得到不同评价对象属于不同等级的综合测度；根据评分准则，实现对评价对象的优劣排序。以往对评价指标进行等级划分时，分成的是若干个互补的等级，这种划分方法会导致等级间信息的重叠，降低等级间的区分度。本文拟将指标分成正常和异常两个对立等级，并在同一等级内部再细分为两个互补小等级，这样既加大了不同类别评价对象的区分度，又保证了相同类别评价对象的区分度，由此减少信息的重叠。其具体步骤如下：

(1)建立测度函数

设有n个评价对象，构成评价空间X={X1,X2,…,Xn}；每个评价对象有m个评价指标；yij为第i个评价对象第j个评价指标的规范化数据，每个指标分为正常和异常2个对立等级，每个对立等级分为2个互补小等级，共形成4个小等级，构成评价空间V={V1,V2}={v1,v2,v3,v4}，其中V1、V2，v1、v2、v3、v4是有序的，满足V1>V2，v1>v2>v3>v4。

yij属于第L个对立等级的未确知测度UijL=U(yij∈VL),L=1,2。因为正常等级和异常等级为对立等级，两等级间无重叠信息，则

(27)

yij属于第l个小等级的未确知测度uijl=u(yij∈vl),l=1,2,3,4。设dj为第j个指标正常与异常等级的分界点，则

a.yij∈V1时，

(28)

b.yij∈V2时，

(29)

UijL与uijl的关系满足：(1)Uij1=uij1+uij2；(2)Uij2=uij3+uij4。同时，UijL和uijl都满足“非负有界性”、“可加性”和“归一性”三条测量准则[22]。

(2)计算综合测度值

由指标权重wj与指标的未确知测度uijl，计算第i个评价对象属于第l个小等级的综合测度uil：

(30)

(3)计算评价对象的健康评分

利用评分准则计算其健康评分，其计算公式如下：

(31)

其中，nl按等差递减数列取值。最终，根据健康评分q(Xi)的大小可对所有评价对象进行健康排序。

3 航空发动机健康状况评估实例

本实例选取某型军用航空发动机地面定检加力状态的22组数据为样本数据[23]。其中，健康发动机样本数据有10组(编号为13～22)，故障发动机样本数据有12组(编号为1～12)。评估发动机健康状况的指标包括：高压压气机静子叶片转角(x1)、进口总温(x2)、滑油压力(x3)、低转子转速(x4)和机匣振动值(x5)。接下来将应用上述评估方法对发动机的健康状况进行评估。

3.1 指标权重的确定

(1)基于G1法的指标主观权重的确定

1)确定评价指标的序关系以及相邻指标的重要性比值

根据专家经验，对以上5个评价指标的重要性进行排序，结果如表2第1～2列所示。其中，序号从小到大，相应指标重要性逐次降低。按照表1的指标重要性比值的说明，得到相邻指标之间的重要性比值，如表2第3列所示。

2)指标权重的确定

根据公式(1)～(2)，得到各评价指标的主观权重，如表2第4列所示。

表2 基于G1法的指标主观权重

(2)基于CRITIC法的指标客观权重的确定

1)原始数据规范化处理

5个评价指标均为固定型指标，则根据公式(5)，得到指标规范化数据。

2)指标所包含信息量的确定

根据公式(7)～(10)得到各评价指标的对比强度、冲突性以及所包含的信息量，如表3第2～4列所示。

3)指标权重的确定根据公式(11)，得到各指标基于CRITIC法的客观权重，如表3第5列所示。

表3 基于CRITIC法的指标客观权重

(3)基于指标难度赋权法的指标客观权重的确定

(4)基于逼近理想点的指标组合权重的确定

将实例中的数据带入规划模型(22)～(26)，化简后的结果如下：

minz=7.2706(w1)2+5.5185(w2)2+

6.7362(w3)2+6.0807(w4)2+5.9657(w5)2

s.t.w3≥w1

w1≥w5

w5≥w2

w2≥w4

θ1+θ2+θ3=1

θ1,θ2,θ3≥0

其中，w1=0.2293θ1+0.2061θ2+0.1568θ3

w2=0.1638θ1+0.2028θ2+0.2799θ3

w3=0.2752θ1+0.1949θ2+0.1880θ3

w4=0.1024θ1+0.2133θ2+0.1688θ3

w5=0.2293θ1+0.1830θ2+0.2065θ3

通过Excel软件求解上述规划模型，得到最优指标权重系数[θ1,θ2,θ3]=[0.2502,0.7220,0.0279]，以及5个评价指标的组合权重[w1,w2,w3,w4,w5]=[0.2105,0.1952,0.2148,0.1843,0.1952]。

3.2 未确知测度模型的建立

(1)测度函数的建立

针对发动机将其评价指标分为健康和故障两个对立等级，形成评价空间V={V1,V2}={健康，故障}。本文利用SPSS软件对各个评价指标进行K-means聚类，得到各评价指标的等级划分，该聚类方法相对于等宽或等频率划分，分类质量和近似精度要更高。等级划分结果如表4所示。

表4 评价指标等级划分

每个等级细分为两个互补的小等级，形成评价空间V={v1,v2,v3,v4}={健康，亚健康，故障，严重故障}。根据公式(28)～(29)，可得到22台发动机各项指标的未确知测度uijl，部分结果如表5所示。

(2)综合测度的确定

由公式(30)得到22台发动机的综合测度uil，部分结果如表6所示。

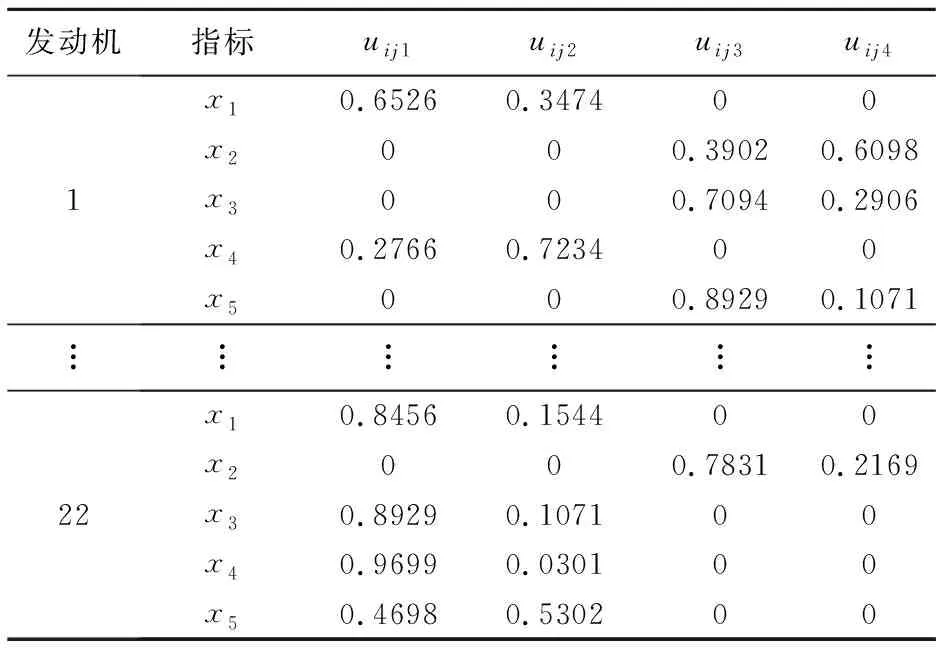
表5 22台发动机各项指标的未确知测度

表6 22台发动机的综合测度

(3)发动机健康评分的确定

4个小等级按照状况最佳10分，状况最差0分的等差数列打分，根据公式(31)得到22台发动机的健康评分，按照健康评分由大到下对发动机进行排序，结果如表7所示。

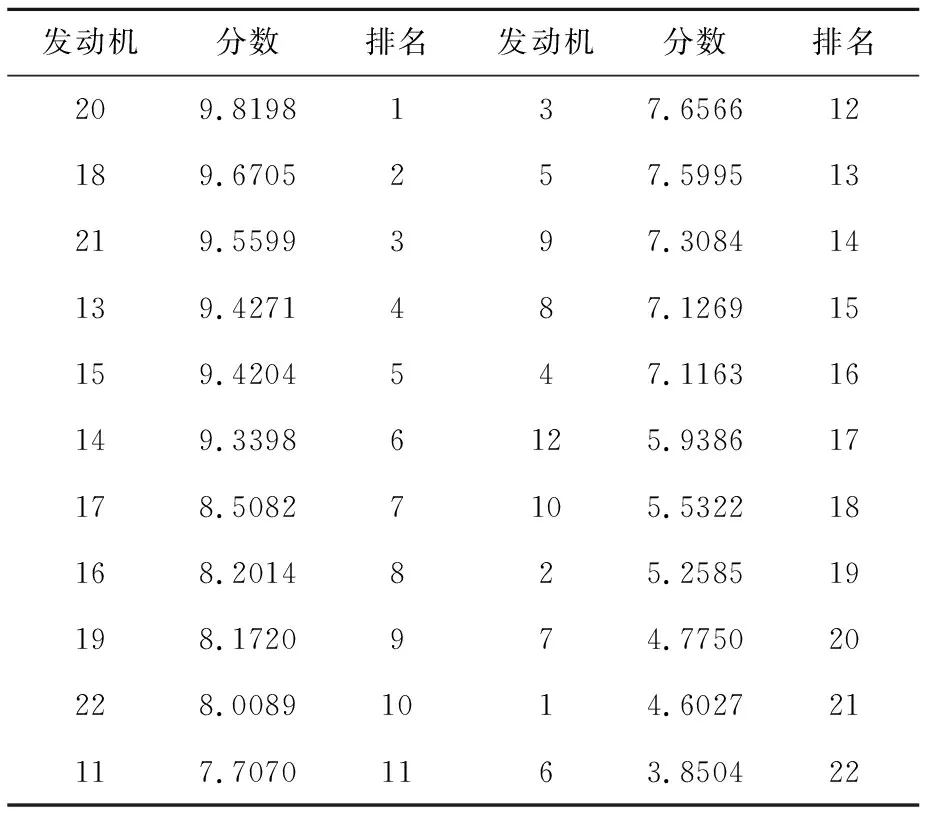
表7 发动机健康状况排序

由表7可知：根据健康评分，健康发动机均排在故障发动机前面。同时，对于22号发动机，尽管排序健康发动机的最末位，但其进口总温(4.744)与机匣振动值(6.27)均明显低于其他正常运行的发动机，说明该发动机性能已经开始衰退，出现故障的概率较大；对于6号发动机，根据健康评分，排序所有发动机的最末位，其进口总温(28)比其他大部分的发动机都要高，滑油压力(1.4)与机匣振动值(50)分别达到了最小极限值和最大极限值，说明该发动机性能已经衰退非常严重。由此可见，发动机的排序与原始数据提供的信息基本一致，即本文对发动机进行健康状况评估的方法具有一定的合理性。

3.3 不同方法的对比

为了进一步说明本文提出方法在评估区分度方面的优势，选择3种组合赋权法——基于逼近理想点的组合赋权法、基于偏差最小的组合赋权法[17]、基于方差最大的组合赋权法[19]和2种评价模型——未确知测度模型、灰色综合评价[17]，将组合赋权法和评价模型相互结合，得到6种不同的评估方法，分别对22台发动机进行综合评估，以健康发动机与故障发动机最终得分的平均值之差为评价指标进行对比分析，结果如表8所示。

表8 不同方法评估结果的对比

由表8可知：在赋权方法上，基于逼近理想点的组合赋权法相比于其他两种组合赋权法，评价对象的区分度更高；在评价模型上，2种评价模型与相同组合赋权法结合时，未确知测度模型相比于灰色综合评价，评价对象的区分度大大提高；在赋权方法和评价模型的结合上，基于逼近理想点的组合赋权法+未确知测度模型相比于其他5种结合方法，评价对象的区分度更高。由此可见，本文所提出的评估方法能够很好地区分健康发动机和故障发动机。

4 小结

在指标赋权方法上，本文通过G1法、CRITIC法、指标难度赋权法分别得到发动机评价指标的主客观单一权重；利用逼近理想点的组合赋权方法得到指标的组合权重。该赋权方法既能发挥主客观赋权方法的优点，又能克服主客观赋权方法的不足，同时在遵守指标权重与指标重要性一致的原则下，提高了健康发动机与故障发动机的区分度。在评价模型上，运用未确知测度模型，对指标进行等级划分时，将指标划分成两个对立等级，同时在每个等级内部，细分为两个互补小等级；基于指标的未确知测度、指标的组合权重和评分准则得到所有评价对象的健康评分。该评估模型通过健康评分区分所有评价对象，另外，通过对等级划分的改进，提高了健康发动机与故障发动机的区分度。通过航空发动机实例分析和方法对比，验证了本文所提出方法对发动机健康评估的合理性以及对健康发动机和故障发动机的高区分性。