起伏非线性振动下倾斜上升管内气液两相流流型转变分析
周云龙,汪俊超,刘起超
(东北电力大学 能源与动力工程学院,吉林省 吉林市 132012)
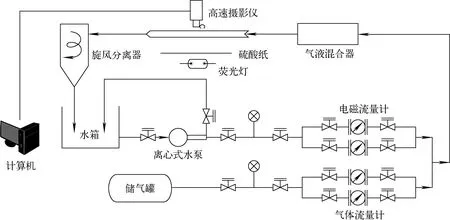
图1 实验系统Fig.1 Experimental system
气液两相流广泛存在于自然界和现代工业生产中,与人类的生活生产息息相关[1]。近年来核动力船舶、漂浮式核能海水淡化设备等迅速发展,这些设备受海浪的作用会发生倾斜、摇摆及周期性起伏振动等状况,影响装置中两相流的流动特性及设备的稳定运行,如摇摆引起的附加惯性力会使气液两相流流型及摩擦阻力改变[2-7]。起伏振动是指向上倾斜管道在竖直方向上做满足正弦函数的往复运动,研究表明振动状态下管内两相流流动特性与非振动条件下有一定区别[8]。
秦梓钧等[9]研究了非振动条件下30°管道内的气液两相流,绘制出流型图。马俊等[10]对非振动条件下大倾角管道的两相流动进行了实验研究,研究表明不同流型对倾角变化的敏感程度有差异。韩洪升等[11]研究了非振动条件下倾角对气液两相流流型变化的影响,绘制流型图并比较流型转换边界的变化趋势。荆建刚等[12]研究了非振动条件下倾斜管道气液两相流流型分类,绘制流型图分析各流型的分布及其变化趋势。周云龙等[13]研究了起伏振动下25°及以下管道内气液两相流流型及其转变边界,分析不同振动条件对流型及其转变边界的影响。
本文对不同起伏非线性振动下不同角度的倾斜上升管内气液两相流流型分布及其转变边界进行研究,揭示振动参数对倾斜上升管内流型转变边界的影响规律,建立振动条件下弥散泡状流-起伏弹状流和准弹状流-液环式环状流转变准则关系式。
1 实验系统
本实验将两相流实验回路与振动装置相连接,实验段固定在振动台上,由电磁式振动台提供非线性起伏振动条件,实验系统及振动装置如图1、2所示。实验段管径为20 mm,两个压力测点间距为800 mm,振动台做频率和振幅可调的正弦运动,振动台上设置振动传感器,测量瞬时加速度。
实验参数设置如下。常温下,设定气体表压为0.125 MPa,气相折算流速Jg为0.1~30 m/s;液相表压为0.1 MPa,液相折算流速Jw为0.1~3.0 m/s。实验设定管道倾角β为20°、30°和45°,振动频率f为2、5和8 Hz,振幅A为2、5和8 mm。
2 实验流型分类
参照Xiao等[14]研究倾角对两相流流型影响的实验及Bhagwat等[15]绘制出的不同倾斜角度下管道内气液两相流的流型图,在间歇性比较显著的起伏弹状流和准弹状流区域内,没有详细划分其他流型,如波环流[15],以免因流型差别不显著对流型的客观辨别产生影响[16]。实验观察到的流型有:弥散泡状流、起伏弹状流、准弹状流和液环式环状流,液环式环状流是本实验条件下新发现并定义的流型。
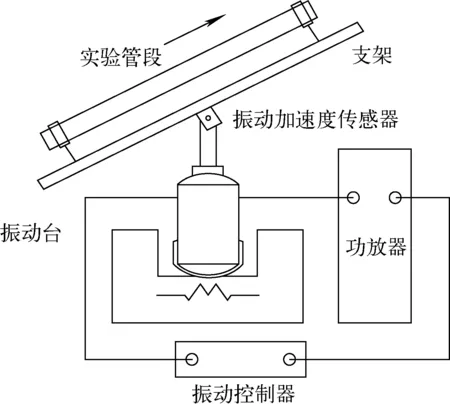
图2 振动装置Fig.2 Vibration device
2.1 弥散泡状流

a——β=30°,Jg=0.1 m/s,Jw=2.6 m/s;b——β=30°,f=5 Hz,A=5 mm,Jg=0.1 m/s,Jw=2.6 m/s图3 弥散泡状流对比Fig.3 Comparison of diffuse bubble flow
气、液相折算流速比值较小时,可观察到弥散泡状流。弥散泡状流气泡密度的大小、分布状况与管道的几何形状、倾角等密切相关[15]。弥散泡状流如图3所示,气相以气泡的形式弥散地分布在连续的液相中。图3a是稳定工况下的弥散泡状流,气泡集中分布在管道顶部且气泡尺寸的变化不明显;图3b是振动工况下的弥散泡状流,绝大多数气泡分布在管道顶部,部分较大的气泡分布在管道中央轴线附近,且气泡尺寸有较为明显的变化。管道作周期性起伏振动,管壁压迫气泡做轴向和径向运动,增大气泡间的挤压作用力,使相邻气泡更容易破裂融合形成较大尺寸的气泡。
2.2 起伏弹状流
气、液相折算流速比值约等于1时,可观察到起伏弹状流,如图4所示,很少一部分气相仍以弥散形式分布,另一部分以长条状的气弹形式存在。周云龙等[13]对起伏弹状流的形成机理、基本特征及流动特点进行了详细分析、描述。由于起伏振动的影响,与图4a相比图4b中气泡较大且气泡中有明显的液相波峰存在。

a——β=30°,Jg=0.6 m/s,Jw=1.2 m/s;b——β=30°,f=5 Hz,A=5 mm,Jg=0.6 m/s,Jw=1.2 m/s图4 起伏弹状流对比Fig.4 Comparison of fluctuant slug flow
2.3 准弹状流
在中等气、液相折算流速比值时[15],可观测到准弹状流,如图5所示。准弹状流位于起伏弹状流向液环式环状流转变的过渡区域,在相当大的气液两相流量范围内存在[17]。准弹状流具有混沌、脉动和相位不确定等的特性。如图5a所示,稳定工况下准弹状流的形成主要受气、液相折算流速比值的影响,液相波峰较为单一且含有大量的弥散气泡;图5b所示振动工况下的准弹状流有多个明显的连续液相波峰,弥散气泡含量较少。

a——β=30°,Jg=1.45 m/s,Jw=0.8 m/s;b——β=30°,f=5 Hz,A=5 mm,Jg=1.45 m/s,Jw=0.8 m/s图5 准弹状流对比Fig.5 Comparison of proto slug flow
2.4 液环式环状流
在气、液相折算流速比值大于42.5~46.3时,可观测到液环式环状流。液环式环状流是实验新发现、定义的一种流型,如图6所示,其主要特点是气相在管道中央轴线附近高速流动,液相分为紧贴壁面的薄层流动和紧贴壁面明显的液环流动。在实验中,液环式环状流占据了环状流的分布区域,具有高流速和间歇特性。如图6a、b所示的稳定和振动工况下的液环式环状流,由于气、液相折算流速比值很大,倾角和起伏振动参数对液环式环状流流型的影响不明显,因此气、液相折算流速比值是液环式环状流的主要影响因素。

a——β=30°,Jg=25.0 m/s,Jw=0.2 m/s;b——β=30°,f=5 Hz,A=5 mm,Jg=25.0 m/s,Jw=0.2 m/s图6 液环式环状流对比Fig.6 Comparison of liquid-ring annular flow
3 实验结果分析
3.1 弥散泡状流-起伏弹状流的转变机理分析
弥散泡状流-起伏弹状流转变的过程中,大量弥散分布的气泡碰撞、破裂、融合形成较大的长条状气弹,且由于管道倾角和起伏振动的存在,气相的存在形式会发生较大变化,流型转变前后气泡的宏观尺度也有较明显的变化。荆建刚等[12]和谢添舟等[18]先后对稳定条件下倾斜管内弥散泡状流-弹状流转变机理进行了详细分析,谢添舟等[18]同时指出气泡所受径向浮力、表面张力和湍流力是决定流型转变的关键因素。基于荆建刚等[12]和谢添舟等[18]有关稳定条件下倾斜管道内弥散泡状流-弹状流转变机理的研究,本文对起伏振动下倾斜管道内弥散泡状流-起伏弹状流转变机理进行分析。
气泡受到的湍流力使气弹破裂分散形成小气泡,湍流力计算方法如下:
(1)
式中:Fgt为湍流力,N;dsg为气泡直径,m;ρw为液相密度,kg/m3;μw为液相摩擦系数,计算式如下[18]:
(2)
式中,Rew为液相雷诺数,计算式如下:
(3)
式中:D为管道直径,m;uw为液相流速,m/s;νw为液相动力黏度,N·s/m2。
气泡所受浮力在管道径向上的分力为:
(4)
式中:Fsg为浮力的管道径向分力,N;ρg为气相密度,kg/m3;g为重力加速度,m/s2。
气泡所受起伏振动附加力在管道径向上的分力为:
(5)
式中:Fsgf为振动附加力的管道径向分力,N;a为起伏振动加速度,m/s2。
当Fsg+Fsgf≥Fgt时,弥散的气泡开始碰撞、破裂、融合形成起伏弹状流,则有:
(6)
Barnea[19]提出了一个在临界状态下单个气泡直径的计算公式:
(7)
式中:α为含气率;σ为表面张力,N/m。
联立式(6)、(7)可得起伏振动下弥散泡状流-起伏弹状流转变关系式:
(8)
式(8)适用范围为:管道倾角为20°~45°、振动频率为2~8 Hz、振幅为2~8 mm。
根据式(8)计算的弥散泡状流-起伏弹状流转变边界与采用荆建刚等[12]关系式的计算值及实验值相比较,结果如图7所示。由图7可见,两种计算方法的计算值均比实验值偏大,但修正关系式所得计算结果与实验值符合更好。
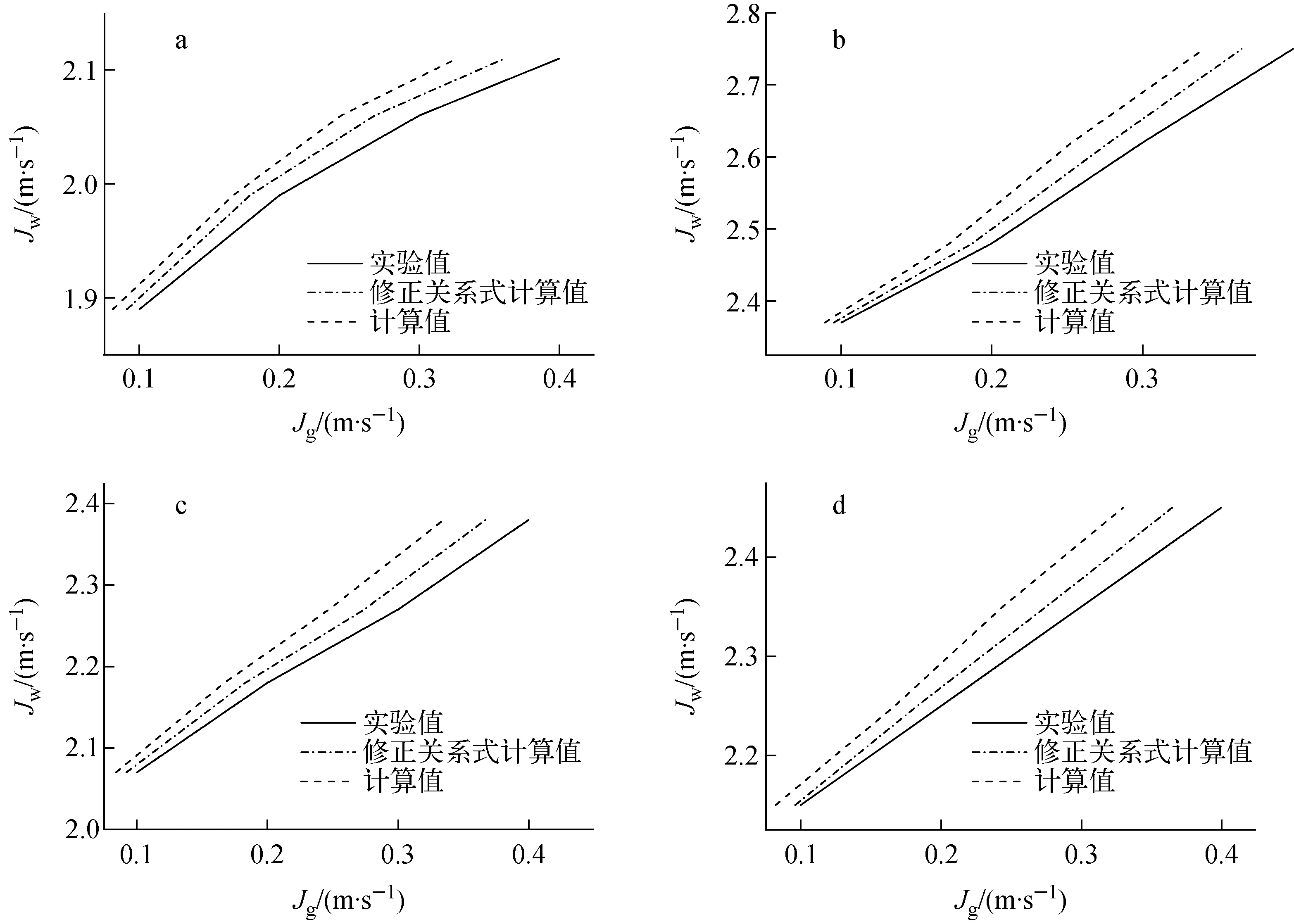
a——β=30°,f=2 Hz,A=5 mm;b——β=30°,f=8 Hz,A=5 mm;c——β=20°,f=5 Hz,A=5 mm;d——β=45°,f=5 Hz,A=5 mm图7 弥散泡状流-起伏弹状流转变边界实验值与两种计算方法结果的对比Fig.7 Comparison between experimental value of transition boundary of proto diffuse bubble flow and fluctuant slug flow and result of two computational methods
3.2 准弹状流-液环式环状流的转变机理分析
在准弹状流-液环式环状流转变区域,当气、液相折算流速比值增大时,液相界面的剪切力不断增大,以至克服液相自身重力,使液相紧贴管壁流动形成液膜;由于倾角和起伏振动,气、液相界面液膜发生滑移,在剪切力、倾角和起伏振动的综合作用达到动态平衡时形成液环,转变为液环式环状流。
气液流速、倾角、界面剪切力、壁面切应力和起伏振动等对液环式环状流的形成有重要影响,借鉴Barnea[19]提出的理想环状流模型,并在曹夏昕等[17]提出的倾斜管内理想环状流模型的基础上,对起伏振动下液环式环状流的形成进行分析。
理想状态下,忽略液环式环状流液膜和液环厚度差异,简化为理想稳定的环状流,对气、液两相进行力的平衡分析。
对液相:
ρwAwgsinβ+ρwAwasinβ=0
(9)
对气相:
ρgAgasinβ=0
(10)
式中:Aw、Ag分别为液相、气相截面积,m2;p为压强,Pa;z为管道轴向距离,m;τw、τg分别为液相、气相壁面剪切应力,N/m2;sw、sg分别为液相、气相湿周,m。
联立式(9)、(10):
(11)
其中:
(12)
(13)
(14)
(15)
式中:fw为壁面摩擦系数;uw为液相流速,m/s;Qw为液相体积流量,m3/s;A为管道横截面积,m2;Cw为修正系数;δ为液膜厚度,m。
由式(11)~(15),可得:
(16)
式中,n为指数。
采用Wallis[20]计算界面剪切力系数fi的关系式:
(17)
式中,fg为不存在液膜时的气相摩擦系数:
(18)
式中:Cg为修正系数;m为指数;νg为气相动力黏度。
气、液两相都处于层流状态时,Cg=Cw=16,n=m=1.0;湍流状态时,Cg=Cw=0.046,n=m=0.2。
根据曹夏昕等[17]和谢添舟等[18]的研究,气相壁面剪切应力τg可用下式计算:
(19)
由式(16)、(19)得:
(20)
式(20)适用范围为:管道倾角为20°~45°、振动频率为2~8 Hz、振幅为2~8 mm。
根据式(20)计算出准弹状流-液环式环状流转变边界,并与曹夏昕等[17]关系式的计算值及实验值相比较,结果如图8所示。由图8可见:两种计算方法的计算值均比实验值大;修正关系式的计算结果更接近实验值,误差相对更小,且频率和倾角越大修正关系式计算值与实验值的相对误差越小。

a——β=30°,f=2 Hz,A=5 mm;b——β=30°,f=8 Hz,A=5 mm;c——β=20°,f=5 Hz,A=5 mm;d——β=45°,f=5 Hz,A=5 mm图8 准弹状流-液环式环状流转变边界实验值与两种计算方法结果的对比Fig.8 Comparison between experimental value of transition boundary of proto slug flow and liquid-ring annular flow and result of two computational methods
本文修正关系式是基于理想稳定的环状流模型,液膜光滑、厚度均匀。而液环式环状流既有液膜又有液环,且实验中的气液分界面呈不规则的起伏状,管道上、下内壁液相厚度也不同,稳定和振动条件下,气、液相摩擦系数也有差别。因此,实验值与两种计算模型的计算值之间会有不同程度的差异。
4 结论
1) 实验工况下,倾斜上升管内气液两相流流型为弥散泡状流、起伏弹状流、准弹状流和液环式环状流。液环式环状流是实验新发现、定义的流型,具有高流速和间歇特征。气、液相折算流速比值大于42.5~46.3时,可观测到液环式环状流。
2) 考虑附加振动的影响,建立了适用于起伏振动下弥散泡状流-起伏弹状流和准弹状流-液环式环状流转变关系式。相对于原关系式,修正关系式的计算结果相对误差更小,与实验值符合得更好。
3) 两种修正关系式的计算结果与实验值均有一定的差别。首先,含气率是影响两种转变关系式符合效果的重要因素,鉴于气液两相流动的不稳定性,实验测得的含气率有一定的误差。此外,对于修正的弥散泡状流-起伏弹状流转变关系式,起伏非线性振动下临界气泡直径的计算模型仍需进一步研究改进;对于修正的准弹状流-液环式环状流转变关系式,则是忽略了液环与液膜的差别及液膜厚度的变化。

