高温、高流速氢气在圆管内流动换热特性研究
房玉良,秦 浩,王成龙,苏光辉,田文喜,秋穗正
(西安交通大学 动力工程多相流国家重点实验室,核科学与技术学院,陕西 西安 710049)
核热推进技术是利用反应堆产生热能将推进剂加热到高温状态,高温工质从喷管膨胀产生高速气流形成推力的新型推进技术,具有比冲高、推力大等优点[1-2]。核热推进系统采用氢气作为推进剂并将其加热到2 500 K以上,产生与化学推进相媲美的推力,比冲可达到化学推进的两倍。核热推进技术研究起源于20世纪50年代,经过美、俄(苏)等60多年的研究,固态堆芯核热推进技术逐渐成熟。美国宇航局在载人火星探测报告DRA 5.0中明确提出将核热推进火箭作为太空摆渡车的首选方案[3]。固态堆芯核热推进反应堆冷却通道可分为轴向型、径向型,其中轴向型通道具结构简单、易于加工制造等优点使其应用更为广泛,如NERVA型堆芯、CERMET型堆芯等[4]。但由于轴向型通道具有很大的长径比,加上堆芯的热流密度、温度很高,因此通道内的物性变化很大,换热特性随之变化。为避免换热特性变差威胁堆芯热工安全,有必要对大长径比通道内冷却剂流动换热特性进行研究。
基于美俄开展的核热推进计划,研究人员开展了大量的氢气流动换热特性理论和实验研究,获取了丰富的研究资料。McCarthy等[5]、Taylor[6-7]、Petukhov等[8]、Perkins[9]、McEligot等[10]开展了涵盖反应堆热工参数的氢气流动换热实验研究,获取了相关的实验关联式。Hess与Kunz[11]对超临界氢气流动换热特性开展理论分析并与实验数据进行了对比,绝大多数数据误差在±20%之内。Sajan[12]针对典型核热推进反应堆堆芯单通道进行了参数敏感性分析。受限于当时实验研究条件的落后和核热推进计划的终止,氢气在反应堆通道内热工水力行为的研究仍存在着一定的缺陷,此外,高温、高流速、高热流密度等特殊环境下的氢气流动换热特性的研究资料较少,相关数值计算模型还不完善。本研究采用数值计算方法开展高温、高流速氢气在圆管内流动换热特性研究,并验证模型及算法计算的正确可行性。
1 数学物理模型与计算方法
1.1 控制方程
本研究基于圆管流道采用二维轴对称模型进行数值模拟,模型假设如下:稳态无内热源,忽略辐射换热、化学反应等。质量、动量、能量守恒方程如下:
(1)
(2)
(3)
div(λ·grad(T))+Φdissipation
(4)
式中:ρ为密度,kg·m-3;u、v分别为轴向速度、径向速度,m/s;x、r分别为轴向位置、径向位置,m;p为压力,Pa;T为温度,K;μ为动力黏度,Pa·s;cp为比定压热容,J/(kg·K);λ为导热系数,W/(m·K);Φdissipation为黏性耗散项。
1.2 数值计算方法
本研究采用商用CFD软件ANSYS FLUENT,求解器为基于压力的耦合方法,同时求解质量、动量方程后再进行能量、湍流方程等标量方程的求解,收敛速度更快,更适合用于控制方程存在较强依赖关系的高速领域。空间离散采用二阶迎风格式。湍流模型采用SSTk-ω模型,并考虑压缩效应和黏性加热效应。
1.3 边界条件
本研究计算模型几何结构如图1所示,其中圆管内径2.95 mm,粗糙度0.44 μm,入口段长度41.25 mm,加热段长度228.60 mm。不计算壁面固体域。计算域边界条件如下。1) 入口:质量流量、温度;2) 出口:压力;3) 入口段壁面:绝热、无滑移壁面、给定壁面粗糙度;4) 加热段壁面:第2类边界条件、无滑移壁面、给定壁面粗糙度。

图1 计算模型几何结构Fig.1 Structure of calculation model
1.4 网格无关性验证
以质量流量m=0.870 6 g/s、入口流体温度Tb,in=315.56 K、出口压力pout,abs=147.33 kPa、壁面热流密度q=1 849 864 W/m2为基础工况进行网格无关性验证,本研究共给出了5套网格,网格信息列于表1。
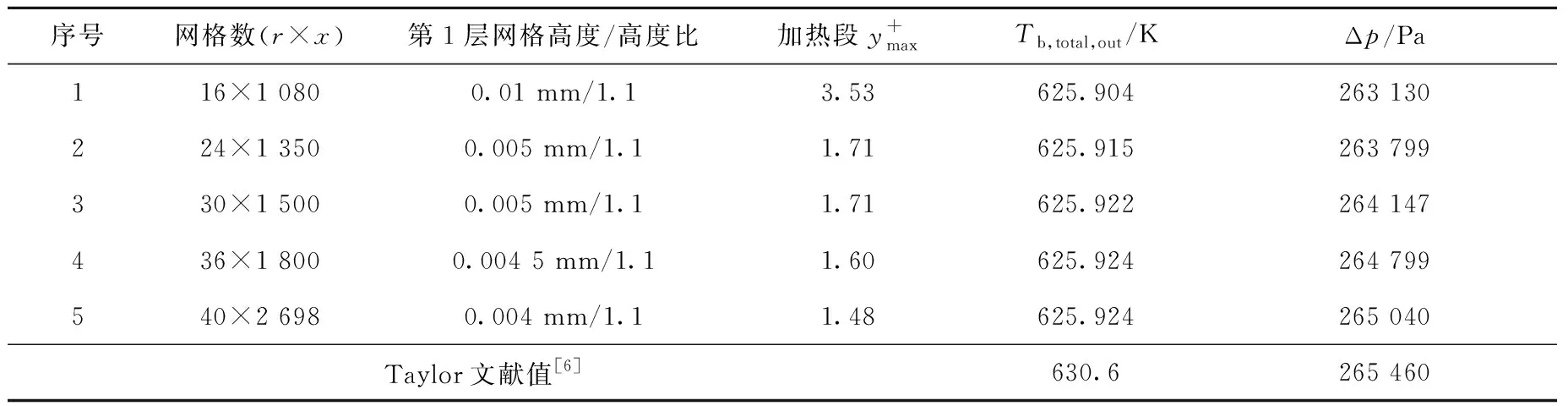
表1 网格无关性验证Table 1 Grid independency verification
以出口主流总温Tb,total,out、进出口压差Δp作为参考量,网格无关性验证结果表明,在节省计算资源和保证计算精度的条件下,选用网格36×1 800即可满足需要。
2 氢气物性模型
氢气属于小分子量(摩尔质量Mmole=2.015 9 g/mol)轻气体,存在两种自旋异构体形态:正氢(Ortho-hydrogen)和仲氢(Para-hydrogen),两者物理性质有所差异,化学性质相同并可相互转化。在室温环境中,处于平衡状态的氢气称为标准氢(normal hydrogen),其中正氢与仲氢体积之比为3∶1。标准氢的临界压力为1.296 4 MPa,临界温度为33.145 K,临界密度为31.262 kg/m3。本研究采用标准氢作为冷却工质进行数值计算,在计算工况范围内,氢气物性变化很大,物性变化对流动换热影响很大,因此本研究采用变物性模型。
2.1 状态方程
计算工况范围温度远超过氢气的临界温度、压力低于临界压力,氢气作为实际气体考虑,状态方程采用Aungier-Redlich-Kwong(ARK)模型:
(5)

2.2 热物理与输运性质
气体分子随温度的升高裂解成更简单的分子或原子,这种现象称为热解或热离(thermal dissociation or atomization)。在足够高的温度下,气体分子可全部热解成原子。在更高的温度下,气体还会发生电离过程,电子从原子中分离逃逸形成等离子体。
常压状态下,氢气H2的热解温度约为1 500 K[13-14],在温度达到5 000 K以上时,H2分子几乎全部热解变成原子氢气体。在核热推进反应堆中,堆芯温度很高且伴有各类放射性射线和高能带电粒子,这导致了氢气分子的电离和热解[15]。
研究结果表明,温度、压力以及堆芯中能量沉积均对氢气热解有重要影响,图2为不同温度、压力下的氢气热解份额[13-14],处于热解平衡状态下的分子氢与原子氢热物性与输运性质发生了很大的变化[16]。物性变化使冷却剂流动换热特性发生变化,欲真实模拟氢气在管内热工水力行为,须考虑高温氢气热解对物性的影响。

图2 氢气热解份额Fig.2 Degree of thermal dissociation of hydrogen
流体的热物理与输运特性取决于温度和密度(或压力),为简化计算过程、节省计算资源,通常拟合为温度和压力的多项式形式。由于工况计算范围内物性受温度变化影响程度远大于压力,本研究忽略压力变化对物性的影响,将物性简化为温度的单值函数。NIST(National Institute of Standards and Technology)给出了氢气物性计算数据库,但温度适用范围上限仅为1 000 K且未考虑高温热解对物性的影响,无法满足计算需要。在相应高温条件下,氢工质为热解平衡状态下的氢原子和氢分子的混合物。本文根据NASA(National Aeronautics and Space Administration)和NBS(National Bureau of Standards)推荐的热平衡条件下氢气物性数据[17]拟合了多项式函数,更适合本文研究。
(6)
式中:Y代表cp、λ、μ等变量;N为系数。
热物理与输运特性列于表2。

表2 氢气低压条件下的热物理与输运特性Table 2 Thermo-physical and transport property of low pressure hydrogen
3 模型验证与换热特性分析
3.1 验证实验
Taylor[6]研究了氢气、氦气在钨金属圆管内流动换热特性,其中热流密度由实验段电阻加热提供,实验段结构与尺寸参数如1.3节所述。实验范围雷诺数Re=7 600~39 500,实验段入口压力0.27~0.70 MPa,Tw/Tb最大值为5.6。
Taylor实验采用电阻式加热方式,即在实验段两侧直接加载电流,由于钨金属圆管材料的电阻率随温度的升高而增大,实验中轴向上的热流密度并不均匀。由式(7)可知,加热段轴向热流密度分布实际为壁面温度的函数。
(7)

本研究选取验证工况列于表3[6]。图3为验证工况热流密度qe和壁温Tw分布[6]。

表3 验证工况Table 3 Verification case
由图3可知,壁温分布与热流密度分布基本一致。在较低热流密度时,如Run1、3、7,实验段前半部分热流密度、壁温分布近似线性,在较高热流密度时迅速上升达到峰值。如Run19、20、21,质量流量基本相同,而随功率输入的增加,两个因素导致加热段入口部分壁面温升较大。首先,Tw/Tb增加伴随着传热系数降低,进一步提高了壁面温度。其次,在较高温度下钨电阻率增加放大了提高Tw/Tb的效果。连接部件传导损耗使加热段入口处和出口处的轴向温度梯度较大。
3.2 结果对比
本研究基于Taylor实验进行验证分析,研究湍流模型对壁温分布的影响。Taylor实验结果处理中考虑了辐射散热、轴向导热等,利用热平衡计算得到了等效热流密度分布,本研究将得到的热流密度分布作为边界条件输入,对比了Standard(标准)k-ε、Realizable(可实现)k-ε以及SSTk-ω等3种湍流模型的适用性,计算值与实验工况值对比结果如图4所示,其中实验工况值的误差带为±10%。结果表明,SSTk-ω模型的适用性较其他两种模型要好得多。这主要是在研究范围内近壁面处温度、速度、物性等变化非常剧烈,湍流动能、比耗散率等很大,而SSTk-ω模型直接穿过黏性底层应用于壁面[18],在近壁面处的处理要优于k-ε模型,因此计算值更接近于实验值。在实验加热段的进出口处,计算值与实验值相差较大,主要原因是计算工况未考虑轴向导热、实验加热段有连接部件传导损耗。此外,实验中还存在测量位置误差、测量仪器误差等。本研究认为,采用SSTk-ω湍流模型计算高温、高流速氢气圆管内流动换热特性是合理可靠的。
3.3 换热特性分析
本文以质量流量m=0.870 6 g/s、入口流体温度Tb,in=315.56 K、出口压力pout,abs=147.33 kPa、壁面热流密度q=1 849 864 W/m2为基础工况,进行热流密度加热条件下变物性可压缩高温氢气流动换热特性分析。通过改变边界条件,研究质量流量和壁面热流密度等热工参数对换热特性的敏感性影响。
1) 流场与温度场分布
本研究对基础工况进行流道内的流场与温度场分布情况分析。由于流道直径较小,氢气密度较低,因此即使入口质量流量很低,入口的速度量级也相当可观。氢气流场与温度场分布示于图5。

图3 验证工况热流密度和壁温分布Fig.3 Heat flux and wall temperature distributions of verification cases
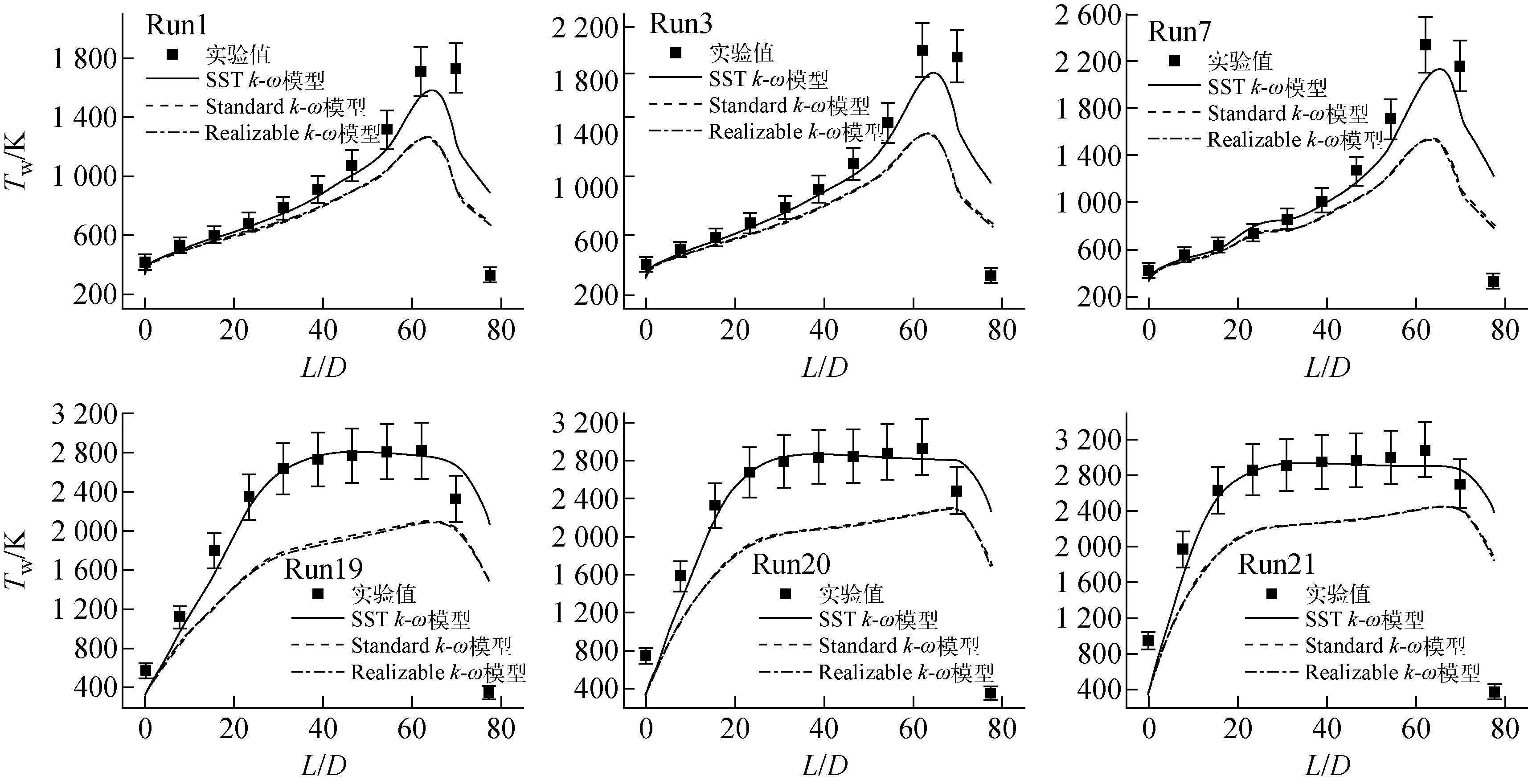
图4 不同湍流模型计算值与实验值对比结果Fig.4 Comparison of calculation values and experiment data under different turbulent models

图5 氢气流场与温度场分布Fig.5 Distributions of flow and temperature fields of hydrogen
由图5可知,随轴向压力的降低、温度的升高,流道内的氢气膨胀密度降低、速度升高,并在靠近出口位置处马赫数Ma>1,实现了跨声速流动。由于入口段效应,壁温与主流温度之比也出现先增大后减小的趋势。此外,黏度、比热、导热系数等物性随轴向主流温度的升高而升高,轴向雷诺数Re、努塞尔数Nu均降低,即管内氢气流动换热变差。近壁面的氢气密度较小、黏度很大形成黏滞力,阻碍了径向传热并加剧了壁温升高,进一步造成壁面与主流温差增大形成正反馈,因此,导致氢气换热特性变差。轴向不同位置处的径向速度与径向温度分布如图6所示,出口位置处的近壁面与中心线温差可达500 K以上。

图6 轴向不同位置处速度与温度径向分布Fig.6 Radial distributions of velocity and temperature at different axial positions

图7 热工参数对流动换热特性的敏感性分析Fig.7 Sensitive analysis of flow and heat transfer characteristics under different thermal parameters
2) 参数敏感性分析
为探究热工参数对氢气在圆管内的流动换热影响情况,将基础工况的入口流量、壁面热流密度分别变化±10%、±20%,进行了参数敏感性分析。其中摩擦因子计算如下。
Δp=pin-pout=Δpa+Δpf
(8)
(9)
(10)
式中:Δp压降,Pa;G为质量流速,kg/(m2·s);f为摩擦因子;下标in、out、a、f、av分别为入口、出口、加速值、摩擦值、平均值。
图7为热工参数对流动换热特性的敏感性分析。结果表明,随入口流量的增大,Nu增大、f减小,即增大入口流量起到了强化换热的效果。入口流量每增大10%,Nu增大10%~11%、f减小约4%。随热流密度的增加,Nu与f均呈下降趋势,即增大热流密度对氢气在圆管内换热不利。热流密度每增大10%,Nu减小3%~4%、f减小不足1%。
当传热壁面与流动气体之间存在较大温差时,流动截面与流动方向上物性变化很大,管内气体传热不再符合一般的定常物性传热关系式。近壁面处的气体温度近似等于壁温,径向上的物性随气体温度变化而变化,而影响气体密度的压力在垂直于流动的横截面上通常是恒定的。因此,考虑变物性、适合于定壁温或定热流条件的气体流动换热关系式采用温度、热入口段修正,即:
(11)
文献中常用的适用于氢气流动换热的实验关联式列于表4[19]。
为研究不同实验关联式的适用性,本研究将计算工况结果与表4的实验关联式展开对比,计算工况Nu[20-21]为:
(12)

表4 氢气流动换热实验关联式Table 4 Heat transfer correlation of hydrogen
式中:Pr为普朗特数;h为对流换热系数,W/(m2·K);下标w、b表示壁面、主流。
图8为计算值与换热模型对比。由图8可知,计算值与实验关联式相对误差均在±6%以内,本研究范围内计算工况符合实验关联式模型的。此外,考虑了温度修正的Miller-Taylor实验关联式与计算值偏差最小,因此本研究推荐该关联式评价圆管内变物性、高温、高流速气体流动换热特性。

图8 计算值与换热模型对比Fig.8 Comparison of calculation value and result of heat transfer model
4 小结
核热推进技术是未来深空探测、载人航天最有竞争力的技术之一,反应堆热工设计又是最关键问题。本文采用数值计算方法开展高温、高流速氢气圆管内流动换热特性研究,可得出以下结论。
1) 采用压力基耦合算法、SSTk-ω湍流模型以及物性模型研究高温、高流速氢气圆管内流动换热特性合理可行,壁温计算结果与实验值符合较好,验证了数值计算模型的选择是正确的。
2) 由于轴向壁温升高,近壁面氢气黏度变大、密度变小,径向传热较差使换热变差,进一步提升了壁温,形成正反馈,因此热工设计时要着重考虑变物性对换热特性的影响。
3) 通过进行入口流量、壁面热流密度等热工参数敏感性分析发现,随入口流量的增加,换热效果增强,随热流密度的增加换热效果变差。研究范围内,本文推荐修正Miller-Taylor实验关联式评价圆管内变物性、高温、高流速气体流动换热特性。

