带有随机订货点的两阶段报童模型
闵 杰, 李 瑶, 刘 斌, 欧 剑
(1.安徽建筑大学 数理学院,安徽 合肥 230601; 2.安徽建筑大学 经管学院,安徽 合肥 230601)
0 引言
在实际生产运营中,由于消费者需求随机性的存在,零售商对某类商品实行一次订购策略往往导致库存不足或库存积压。订货不足会导致商品缺货损失;反之,若一次订购量太多,为减少库存成本,快速回笼资金,零售商在销售期末只能将积压的库存商品以一个低于成本价的售价清仓处理。所以,传统的一次订购策略可能导致供货服务水平降低和零售商利润受损。针对一次订购的缺点,一些零售商采取了在销售周期内实行二次订购的策略来规避市场风险,提升利润。
然而,由于工艺、产能、原材料或管理等因素的限制,当零售商进行第二次订货时,上游商品制造商可能无法及时满足零售商的采购需求,只有当上游制造商生产的商品库存满足零售商二次订购的需求时才能保证商品的及时供应。所以,零售商第二次订货成功的时间点存在不确定性,本文将其称为“随机订货点”。这种现象普遍存在于现实生活中,如“国货之光”小米手机在每次新品发售之前会根据预测的市场需求进行第一次订货,但是在整个销售期内仍会出现新款售罄的情况,当零售商根据市场空缺再次补货时,上游制造商可能因为产能或者原材料不足等原因无法准确把握供货时间,因此,小米零售部门的第二次订货时间也就存在随机性。这种现象在很多行业的供应链运作中很常见,如服装行业的某种爆款服装、章丘铁锅等,这些热销商品都会出现因断货而导致第二次供货时间不确定的情况。本文依据这些实际情况,研究了第二次订货时间点不确定的报童问题。
对于报童问题,很多学者进行了深入研究,从单周期到多阶段[1,2],甚至到整个供应链问题[3~6],从一次订购拓展到可追加订购问题[7~11]。Lau等[12]研究了带有二次订购的单周期报童模型,分析了零售商在两次订购机会下的最优订购量和整个销售期的最优期望利润。王圣东等[13]考虑了有缺货损失情况下的两阶段需求独立的报童模型,并在此基础上延伸了两阶段需求相关的报童模型,给出了零售商的最优订购量,使得其获得最大的期望利润。侯云章等[14]研究了只有一个零售商和一个供应商的二级逆向供应链系统,在两个阶段的需求均服从正态分布的情况下,采用信息不共享的二次订购策略时,零售商和整个供应链的总收益,并与一次订购模型进行比较分析,通过数值算例说明二次订购策略可以优化整个逆向供应链系统。王圣东等[15]考虑了两次订货机会下由单个制造商和多个销售商组成的供应链生产、销售易逝品的协调模型, 给出了模型的解析解。宋海涛等[16]只考虑第一次销售需求量,研究了带有两次订购、两次销售的报童模型。在宋海涛等人的研究基础上,文献[17]基于需求分布的不同,通过假设两次需求独立且服从不同分布,建立了订购量与企业收入之间的映射关系,最后详细探讨了需求服从均匀分布时的特殊情况。以上文章都研究了二次订购的报童模型,但是均假设第二次订货时间点是确定的,而未考虑到时间因素的影响。
另外一些文章分析了时间因素对报童模型的影响,如蔡清波等[18]考虑了带有采购时间的一般报童模型,假设市场需求预测值的方差是采购时间的线性函数,当需求量服从均匀分布时,零售商应如何确定采购时间和最优的订购量,使得自己在销售期内获得最大的期望利润。李明琨等[19]在传统报童模型中加入了提前采购的天数,并分析了需求量服从不同分布,且能够采购到的货物量、采购成功的概率和进货价格三个因素分别为时间函数时,零售商的最优订购量和最小的期望损失。贺勇等[20]分析了带有提前订货期的传统一次订购模型,利用计算机仿真的方法求得在订购时间、库存成本和最高订购数量具有时变性质下的最优订购时间和最佳订货量,并以一个实例进行了计算分析。但是这些模型并没有将时间因素体现在销售期的两个阶段上,未考虑第二次订货时间点不确定的两阶段订货情形,然而在实际中普遍存在零售商二次补货且补货时间不确定的现象[21]。
本文站在零售商的角度,为了让零售商获得最大的期望利润,以联系实际和研究以上文献为基础,构建了含有随机订货点的两阶段报童模型,在满足随机订货点和需求率同时服从均匀分布的情况下,所决策最优的订货量。通过具体案例对模型进行讨论,并对比分析了传统一次订购报童模型和订货点具有随机性的二次订购报童模型的期望总利润,得出相应的理论贡献与管理启示。
1 模型符号与假设
为便于表述,将本文所用符号与假设描述如下:
(1)对销售周期归一化处理,将整个销售期假设为[0,1];
(2)若上游生产商货源充足,则及时供货;
(3)假设零售商第二次订购时刻为t,且t为服从均匀分布的随机变量,即随机订货点t~U(0,1);
(4)将销售周期内的市场需求率表述为r,假设单位时间的随机需求量r~U[a,a+h],其中,a≥0,h>0,且整个销售期内各时刻的需求率相同;D为整个销售期间的总需求量,Di(i=1,2)分别为第一阶段和第二阶段的需求量,且D=r·1=r,D1=rt,D2=r(1-t);
(5)Qi(i=1,2)分别表示前后两次的订货数量;
(6)将c表示单位商品的采购成本,p表示为单位商品的零售价格,s表示单位商品的缺货所造成的损失成本,v表示单位商品的回收处理价格,也即商品的残值。根据实际,不难看出p>c>v。
2 模型的构建
我们考虑在单周期情况下带有二次订货的报童模型,并且在该模型中,只有一个零售商和一个生产商。在销售期开始(即0时刻)时,零售商采购第一批数量为Q1的商品;然后根据市场实际需求,在随机的t时刻订购第二批数量为Q2的商品。根据两个阶段的需求率与销售时长,得出第一阶段的需求量D1=rt,第二阶段的需求量D2=r(1-t)。所以,在一个完整销售周期内的市场总需求量D=r·1=r。
销售期内的事件顺序图如下:

图1 考虑订货点随机性的两阶段报童模型事件顺序
基于模型中市场需求率r在一个销售期内保持不变的假设,零售商在销售期内可获得市场的需求信息。然而,在第一次订货时,销售期未开始,需求率r和二次订货时间t对零售商来说是不确定信息,即第一阶段的需求量D1=rt存在随机性,在第一阶段末,商品的剩余量为(Q1-rt)+,这里(a)+=max{a,0},缺货量为(rt-Q1)+;零售商在t时刻进行第二次订货时,此时需求率r和第二阶段的长度1-t已经确定,故第二阶段的需求量D2=r(1-t)是确定的,那么零售商的第二次订货定会满足市场的需求,此时订货量Q2=max{r(1-t)-(Q1-rt)+,0},缺货量为0。因此,整个销售期的销售量为min{Q1+r(1-t),r},订货总量为Q1+max{r(1-t)-(Q1-rt)+,0},缺货量为(rt-Q1)+,销售期末剩余量为(Q1-r)+。

π=π(r,t)
=p·min{Q1+r(1-t),r}-
c(Q1+max{r(1-t)-(Q1-rt)+,0})-
s(rt-Q1)++v(Q1-r)+
(1)
式(1)应分成三种情况考虑:
①当Q1 ②当rt≤Q1 ③当Q1>r时,零售商在第一次的订货量可满足一个完整销售周期的总需求,第二阶段不仅无需补货,且销售期末仍有剩余库存。 用EΠ表示零售商在一个销售期内的期望利润,则当第一阶段订货量为Q1时,零售商的期望利润为 EΠ(Q1)=E(π)=∬π(r,t)f(r,t)drdt 由于r~U[a,a+h],t~U(0,1),且r与t相互独立,所以r与t的联合概率密度函数为 根据Q1的范围,应考虑三种不同的情形: 情形10 图2 情形1下的r-t取值范围的划分 则整个销售期的期望利润为 (2) 情形2a 则整个销售期的期望利润为 (3) 图3 情形2下r-t取值范围的划分 情形3Q1>a+h。 综上所述,零售商在一个销售周期内的期望利润为 (4) 当Q1在区间(0,a]时,为求出φ1(Q1)的最大值,首先对其求一阶导函数: (5) 再考虑Q1在区间(a,a+h]时φ2(Q1)的最大值。由于一阶导函数 (6) (7) (8) 因此,整个销售期内的最优期望总订购量为 (9) 某超市以p=200的销售价格出售某款电子商品,每件商品的采购成本c=100元。如果在一个销售周期结束该商品仍未售完,则零售商以每件商品v=50元清仓处理;若在销售期内缺货,则每件商品的缺货损失为s=120;该商品在销售期内的需求率,即r~U[50,120]a=50,h=70;机会订货点t~U(0,1)。 如果只进行一次订购的话,通过计算可得零售商的最优订货量为Q*=107.037,整个销售期的期望利润为Eπ*=7074.074。 以上例为基础,通过设置v和s分别变化,研究带有随机订货点的二次订购报童模型(以下简称二次订购模型)与传统一次订购报童模型(以下简称一次订购模型)的最优订货量和期望总利润的变化。具体数值结果如表一、表二和图四所示,其中p>c>v。 表1 当p=200,c=100,s=120时,二次订购模型与一次订购模型随v变化的比较 表2 当p=200,c=100,v=50时,二次订购模型与一次订购模型随s变化的比较 图4 在不同成本下期望利润关于v和s的变化曲线 结合图4和表1、表2我们发现,在订货点具有随机性的二次订购报童模型中,零售商的期望利润与商品残值v成正比,与缺货成本s成反比。通过对图4的分析,我们可以得到三个结论:第一,当c固定时,期望总利润的增速与v成正比,其降速与s成反比。这意味着,零售商期望利润对折价损失v的变化比缺货损失s更加敏感。因此,在成本有限的情况下,追求更高利润的零售商在实行二次订货策略时应当全面考虑缺货损失和折价损失。第二,当s不变时,c越低,零售商的期望总利润对v的变化越敏感,说明对于成本较低的商品,残值对期望总利润影响较大。第三,当v不变时,c越高,零售商的期望总利润对s变化的敏感度也随之升高。这一结果表明商品的采购成本越高,则因该商品库存不足导致的缺货损失对零售商利润的负面影响也就越大。 本文基于单周期两阶段报童模型,将研究拓展到第二次订货时间点具有随机性的情形中。通过考虑订货时间点和市场需求都服从均匀分布来构建二次订购的报童模型,最后结合实际案例对比分析了该模型与传统报童模型的优劣。研究结果表明具有二次订购能力且订购点随机的零售商能获得更高利润。对于某类采购成本较小的商品,由商品缺货带来的利润损失影响较小,而由库存剩余导致的折价损失对零售商利润的影响较大。因此,零售商若追求自身利润最大化,必须对成本、缺货损失和折价损失的变化情况进行综合考虑以选择合理的订货量。本文只考虑了随机订货点和需求率为均匀分布的情况,进一步可以考虑随机订货点和需求率服从一般分布的情况,另外,在很多情况下两次订货的成本并不相同,这也是下一步的研究方向。





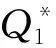
3 销售期的最优订货量
3.1 第一阶段的最优订货量


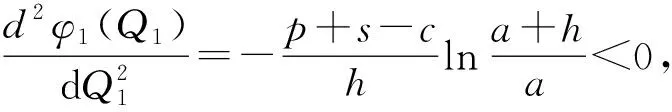
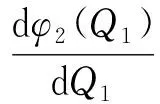


3.2 第二阶段的期望订货量




4 数值算例





5 结束语

