交货期差异下的双渠道订货与协调优化策略

徐 飞, 王红蕾

(贵州大学 管理学院,贵州 贵阳 550025 )

0 引言

互联网+的兴起颠覆了传统多级分销体系，使得消费者不受时空限制而有更大的商品选择范围，也促进了电子商务市场的高速发展。例如，根据市场研究公司Adobe Analytics的数据显示2018年黑色星期五当天，全美在线销售创下62.2亿美元的纪录，同比增长23.6%[1]。中国仅仅天猫在“双十一”当天的成交额高达2135亿人民币[2]。由此可见，电子商务经济在经济全球化中所发挥的作用愈发显著。然而尽管国内互联网红利使得零售电商经历了高速增长期，但是，艾瑞咨询报告显示线上对线下零售市场的渗透率仍未超过20%[3]。尤其是随着纯电商模式平台推广成本持续上涨，线上的价格优势将逐步失去。因此，价格方面所导致的渠道冲突问题将进一步弱化，转而是营销、服务等竞争将导致新一轮的渠道冲突[4]。然而，营销、服务等往往具有较强的外部性，供应链成员通常通过合作解决外部性问题，继而可以解决线上线下渠道的冲突问题，因此线上与线下渠道的合作将成为双渠道供应链的主流范式。

供应链成员通过互惠的合作关系以实现长期利益最大化，很多文献对此进行了研究。例如，肖剑等考虑制造商在电子渠道领域和零售商进行合作，把电子渠道的订单全部交由零售商来完成，通过收益共享建立了基于Stackelberg博弈的理论模型，发现某些情形下制造商线上渠道和零售商合作是最优策略[5]。Chen 和Chang 分析了供应链成员的合作策略，该策略不仅增强了合作成员的竞争优势，而且给供应链带来更多的收益[6]。在此基础上，但斌等构建了由一个制造商与一个零售商组成的双渠道供应链模型，从电子渠道与传统渠道合作的角度出发，研究了双渠道供应链协调的补偿策略，论证了这种补偿策略能够实现双渠道供应链协调[7]。Chen等研究了双渠道供应链中基于Stackelberg博弈的定价及契约问题，提出了使双渠道供应链协调的收益共享契约[8]。Ryan等对价格敏感性的产品探讨了渠道间的合作问题[9]。赵连霞等研究了制造商考虑不开辟网络直销与开辟网络直销渠道同时执行利润共享的定价策略，研究表明制造商在开通网络直销渠道时,有必要通过适当的利润共享与相关零售商实现供应链共赢[10]。林贵华等通过Stackelberg博弈方法研究了供应链中双渠道制造商参与下不同合作策略对供应链中企业的定价和利润的影响，其研究表明合作策略不仅增加了合作联盟的利润，而且也能够增加合作联盟外其他成员的利润[11]。Yan等建立了一个理论框架去研究制造商和线上零售商是否开辟市场渠道问题，建立了二者合作双赢的区域参数[12]。

上述文献主要从最优化理论的角度去考虑合作问题，其并未涉及具体的合作方式。现实中，其合作方式一般通过一定的载体去进行合作，例如从广告、服务、顾客以及渠道等角度去研究线上线下合作的问题。Li等在供应链合作广告模型中研究了合作对投资效率水平的影响[13]。Xie等在一个闭环供应链中通过合作广告研究了线上与线下的合作问题，设计了收入共享契约实现了二者协调[14]。Zhang和Wang在双渠道供应链中考了服务水平和动态定价的合作策略，设计了一个两部制契约进行协调[15]。Feng等将顾客的行为纳入到了双渠道供应链中，设计了契约机制[16]。Sadeghi等则从渠道差异化的角度去研究了合作问题[17]。

上述文献以具体的合作方式研究了线上线上的合作问题，然而其未涉及交货期的问题。现仅有四篇文献研究了双渠道供应链含有交货期的合作问题。Xiao研究了由单个制造商和单个零售商组成的供应链与一个集成供应链(制造商)的价格承诺交货期竞争决策并分别设计了承诺交货期内生和价格内生情况下的供应链协调机制[18]。Modak等研究了销售价格与交货期共同影响需求的线上线下系统，分别分析了集中与分散决策情形下的最优决策，并设计了协调契约[19]。Nekoiemehr等在一个动态环境下研究了制造商与零售商组成的系统，通过对虑交货期的决策实现了对订单的跨期分配[20]。Yang等研究了双渠道中制造商与零售商的合作问题，其合作方式是通过订单的转移来实现。在交货期与销售价格共同影响需求的情形下，研究了零售商与制造商相互合作下的最优交货期以及销售价格，并设计了相应的协调契约[21]。然而，该文献通过交货期影响需求函数方式来实现对需求影响，并且在双方合作时并未体现交货期的影响。

基于此，本文以一个开辟线上渠道的制造商和一个线下零售商组成的双渠道供应链为研究对象，通过考查不同的交货期对订单转移的内生影响，探讨制造商开辟的线上渠道与线下零售商订货与协调机制，并进一步研究交货期差异率如何影响订货等问题。

1 模型定义与假设

考虑一个制造商(M )与线下零售商(R )组成的供应链系统，其中制造商开辟了线上渠道，如图1所示。制造商以单位生产成本c生产一种产品，并以批发价格w(w≥c)销售给线下零售商(以下简称线下渠道)。线下渠道根据需求预测，在需求实现之前进行订货，其订货量为Qr；同时线上渠道根据需求预测进行订货，其货量为Qe，制造商根据二者订货量Q(Q=Qe+Qr)进行生产。线上与线下渠道的销售价格分别为re和rr，销售期末的单位残值为si，单位缺货损失为pi。线上顾客与线下顾客的需求分别为De和Dr并且服从累积分布F(·)和G(·)，其密度函数分别为f(·)和g(·)，且相互独立。

图1 双渠道供应链结构图

按照Xing等对顾客的分类，线下顾客由于其具有较短的交货期要求不会到线上渠道进行购买，而线上顾客可以忍受较长的交货期[22]。所以，当线上渠道不能满足顾客交货期需求时，制造商可以选择与线下零售商合作，将部分不能满足需求的顾客转移给线下零售商，这样可以使得双方互惠：制造商收取服务费而获益，线下零售商获得额外订单而获益。也就是说，由于交货期的差异，制造商的线上渠道可以将其未满足需求的订单转移给零售商的线下渠道，而反之则不行。因此，当线上渠道将线上订单转移给线下渠道时，线上渠道收取服务费τ。然而，由于外部替代性，并非每个线上顾客都愿意被转移给线下渠道。参照文献[23～27]对交货期的刻画，顾客需求与自身交货期呈反向关系，与对方交货期成正向关系。因此本文假设线上与线下渠道交货期差异越大，由线上顾客转为线下顾客比例的越大。所以在此定义交货期差异率θ，0≤θ≤1，进一步假设由此导致未满足需求的顾客有kθ的比例由线上渠道转为线下渠道，其中k为顾客对交货期敏感系数。为了进一步简化后续模型，假设k=1，也就是说，θ表示由于线上渠道交货期的差异使得未满足需求的线上顾客有θ的比例愿意被转移到线下渠道。

从上述流程可知，线上渠道将订单转移给线下渠道将获利为τ，而线下渠道将获利rr-τ。如果线下渠道有多余库存，且满足rr-τ≥sr，线下渠道才会受利益驱动接受线上渠道转移的订单。

2 双渠道供应链基准决策模型

2.1 不考虑合作行为时基准模型

当考虑线上渠道与线下渠道独立决策时，制造商不会将未满足需求的顾客订单转移给线下渠道，此时θ=0，线下渠道的订货行为为经典报童模型，其期望利润函数为:

(1)

对式(1)进行优化得到其最优订货量为：

(2)

当不考虑合作行为时，线上渠道的订货行为也为经典报童模型。我们假定制造商批发产品给线下渠道时，其批发价格为外生参数w，而且二者同时决策，因此其期望利润函数为：

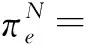
wQr-c(Qe+Qr)

(3)

对式(2)进行优化得到其最优订货量为：

(4)

2.2 考虑合作时分散决策下基准模型

当考虑线上渠道与线下渠道进行合作时，当线上顾客的需求不能满足时，此时制造商可以选择与线下渠道进行合作，即将未满足需求的线上顾客转移给线下渠道，则其未满足需求顾客订单转移量为Ter=min{(Qr-Dr)+,θ(De-Qe)+}，并且线下渠道每个转移订单需要付给线上渠道服务费τ，从而分别建立线上渠道与线下渠道的利润函数:

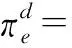
wQr-c(Qe+Qr)

(5)

等式右边分别为期望销售收益、服务费收益、期望残值、期望缺货损失、批发收益，以及生产成本。

sr(Qr-Dr-Ter)+-pr(Dr-Qr)+]-wQr

(6)

等式右边分别为期望销售收益、期望合作收益、期望残值、期望缺货损失以及订货成本。

图2 线上渠道与线下渠道订货与需求

为了方便的对式(5)、(6)进行分析，需要将未满足需求顾客订单转移量Ter=min{(Qr-Dr)+,Q(De-Qe)+}分类进行讨论。因此按照线上渠道与线下渠道的订货量与需求量，可以分为五类情形，分别如图2所示。

线上渠道与线下渠道在情形1、2、3均不会产生合作行为，在情形4、5会产生合作行为。情形4与情形5均表示线上渠道需求过大，而线下渠道库存有剩余，均需要将未满足需求顾客订单转移给线下渠道。但是，二者又有所差别。情形4表示线上需求过大，导致线下渠道的剩余库存Qr-Dr未能满足线上转移的顾客需求θ(De-Qe)，那么其实际转移量为Qr-Dr。而情形5表示线下渠道剩余库存过大，剩余库存能够完全满足线上渠道转移的顾客需求，其实际转移量为θ(De-Qe)。具体需求与订货量情况如表1所示。

表1 不同情形下的订单转移量

结合图2以及表1顾客订单转移量的5种情形，进一步由式(5)和(6)得到制造商与线下渠道的期望利润函数:

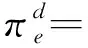
(7)

等式右端第一项代表情形1与2的利润函数，第二、三、四项分别代表情形3、4与5的利润函数,第五、六项分别是批发收益和生产成本。

在本文提出的2个认证阶段中，群组轻量级认证阶段用预先设置随机数的方式，将秘密值提前安全存储在用户移动端和传感器端，并借助发起验证时的时间戳，对用户和传感器群组进行身份认证。无论用户还是传感器群组都无法在自身硬件中篡改或伪造随机数，即使恶意用户对时间戳进行成功伪造，也仅能完成单向认证过程。在该阶段中，用户和传感器群组需要完成双向认证才能证明其身份的真实性。

(8)

等式右端第一项代表情形1的利润函数，第二项代表情形2、3的利润函数，第三、四项分别代表情形5、4的利润函数，第五项是订货成本。

由于差异交货期的存在，使得线上渠道与线下渠道之间的订货行为存在一定利益依存与对抗关系。也就是说，由于线上渠道可以将订单转移给线下渠道而提高收益，因此，线上渠道可以通过订货量控制转移给线下渠道订单的数量，这也必将影响到线下渠道的订货策略。同样，线下渠道也可以通过控制订货量来控制接受线上渠道转移的订单量，从而影响线上渠道的收益，进而影响其订货量。因此为了考查二者的订货行为，就首先必须要保证订货纳什均衡的存在性。定理1给出了二者订货数量纳什均衡的存在性与唯一性。

定理1在线上渠道与线下渠道合作的情形下，当满足rr-τ≥sr时，线上渠道与线下渠道订货数量存在唯一的纳什均衡。

证明通过分别对式(7)、(8)对Qe，Qr进行优化得到：

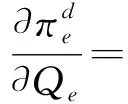
θ(τ+pe)βe(Qe,Qr)+re+pe-c

(9)

(rr-τ-sr)βr(Qe,Qr)+rr+pr-w

(10)

定理1表明由于线上渠道与线下渠道的合作关系，二者的订货数量存在一种替代关系，这也是二者通过订单转移合作的价值所在。这种订货数量纳什均衡的策略性替代关系使线上渠道与线下渠道之间实现了订货数量的“共享”合作行为，从而平衡了二者在销售季节初期的订货量。

为了探讨交货期差异率θ对线上渠道与线下渠道订货的影响机制，首先要得到线上渠道与线下渠道的最优订货量，然后考查对交货期差异率对订货量的影响机制。

(11)

(12)

然后采用隐函数定理分别对式(11)、(12)对求θ导，并且整理得到式(13)、(14)：

(13)

(14)

在式(13)、(14)中，其中

由上式以及上述假设可判定

命题1表明，当线上渠道与线下渠道之间不存在通过订单转移合作时，式(11)、(12)退化为式(2)、(4)。因此，报童模型为有合作行为情形下的特殊形式。

命题1还表明了制造商和线下零售商的互惠行为，制造商的利他行为体现在：交货期差异率越大，则未满足需求的顾客由线上渠道转移到线下渠道的概率越大，因此对线下渠道库存的需求也就越大，导致了其订货量也就越大；线下零售商的利他行为体现在：对于线上渠道而言，由于线下渠道订货量加大，这也提高了线上渠道的服务收益。所以在顾客需求不确定的情形下，线上渠道为了避免期末过高的剩余库存，采取减少订货量而通过提高服务费收益的方式提高其总收益。

定理1与命题1考虑了线上渠道与线下渠道独立决策情形的订货行为，下面考虑集中最优决策情形下的最优化问题，以便为第三部分的协调机制设计提供依据。

2.3 考虑合作行为时集中最优决策下基准模型

证明参照图2及表1对订单转移的分析，由此建立线上渠道与线下渠道组成的整个系统的利润函数:

πc(Qe,Qr)=E[remin{De,Qe}+rrmin{Dr,Qr}+

rrTer+sr(Qr-Dr-Ter)+]+

E[se(Qe-De)+-pe(De-Qe-Ter)+-

pr(Dr-Qr)+]-c(Qe+Qr)

(15)

等式右边第一、二项分别为线上渠道与线下渠道期望销售收益，第三项为线下渠道订单合作期望销售收益，第四、五项分别为线上与线下渠道残值处理收益，第六、七项分别为线上与线下渠道缺货损失，第八项为生产成本。对式(15)进行优化得到:

βe(Qe,Qr)+re+pe-c

(16)

sr(βe(Qe,Qr)+G(Qr)F(Qe))+rr+pr-c

(17)

可以判定二阶海瑟矩阵负半定，即πc(Qe,Qr)是关于(Qe,Qr)的联合凹函数，因此系统存在最优订货量 。由于利润函数为连续函数，因此通过分解总可以得到

w=(sr-rr-pr)(G(Qr)-G(Qr)F(Qe)-βe(Qe,Qr))+c

=(sr-rr-pr)βr(Qe,Qr)+c≤c

由命题2得知，由线上渠道与线下渠道组成的整个系统的利润要大于独立决策时的二者利润之和。其原因在于双重边际效应的存在，即线上渠道与线下渠道独立决策订货时，并未考虑到二者订货量的替代效应，忽视了订货决策时对对方订货量的影响。这就需要设计一定的契约消除独立决策时存在的双重边际效应，从而达到线上渠道与线下渠道的双赢。

3 供应链合作协调机制设计

命题3在线上渠道与线下渠道合作的情形下，当满足ri-τ≥si及w≥c时，无法实现线上渠道与线下渠道的协调。

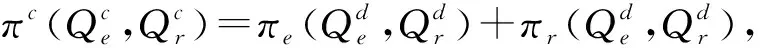
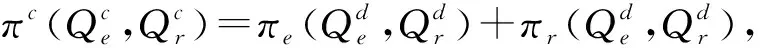
定理2表明，在线上渠道主导下，两部定价协调机制实现了线上渠道与线下渠道的共赢。现实中往往是线上渠道处于强势地位，通过向线下渠道支付固定费用，从而弥补收取的过高的服务费，这样可以使得线下渠道的利润增加，也愿意接受线上渠道提供的激励机制。同理，线上渠道通过支付给线下渠道固定费用，从而将未满足需求的订单转移到线下去销售，避免了顾客的流失，本定理为现实中的企业进行带竞争行为的合作提供了有力的理论依据。

4 算例

为了得到更直观的结果，在数值试验中进一步探讨交货期差异率θ、服务费τ对线上渠道与线下渠道订货量的影响，以及服务费τ对线上渠道与线下渠道订货纳什均衡的影响。假设线上渠道与线下渠道的需求服从Di～U[0,100]，其它参数re=rr=40，se=sr=5，pe=pr=10，w=20，c=10。结合上述参数，根据第2、3节中的理论分析进行求解，并运用MATLAB 9.0软件编写程序绘出图3～图6。当需求服从Di～U[0,100]时，为了便于计算，首先得到以下计算式:

首先，我们考查交货期差异率θ对分散决策情形下订货量的影响。从图3与图4中可以看到，线上渠道订货对交货期差异率递减，而线下渠道订货对交货期差异率递增。这与命题1是一致的。另外，可以从图3、图4中得到，线上渠道收取的服务费越高，线上渠道订货量越小，这与我们直觉是不一致的。其原因在于，在交货期差异率不变的情形下，由于需求的随机性导致了线上渠道通过减少订货量来增加服务费的收益，体现了线上渠道与线下渠道的互惠效应。对于线下渠道而言，线上渠道收取的服务费越高，其订货量越大，其原因在于对于线下渠道而言，服务费越高，其得到一个订单的成本越大。所以，在交货期差异率不变的情形下，其最优决策是增加订货量。

图3 线上渠道订货与θ关系

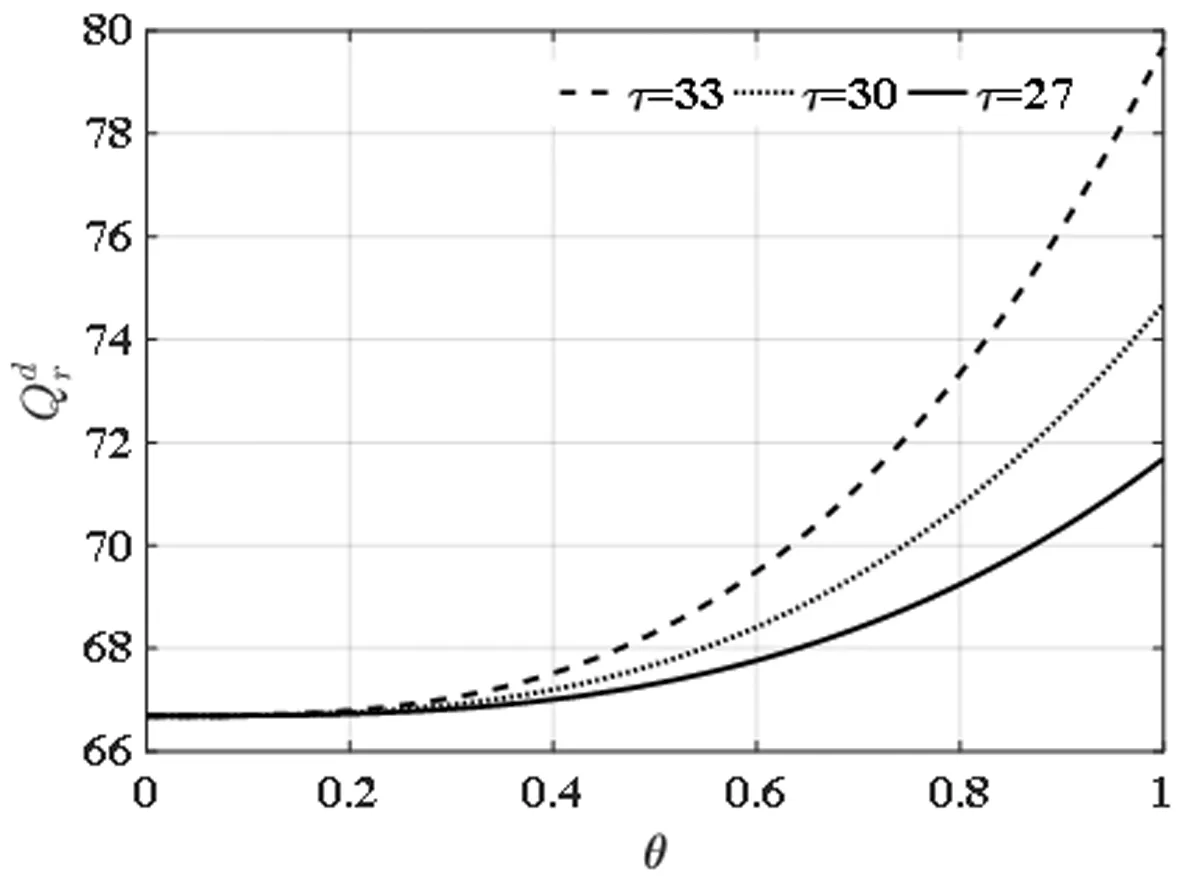
图4 线下渠道订货与θ关系

其次，考查线上渠道与线下渠道订货纳什均衡的存在性。在τ=27，τ=30的情形下我们得到二者分散决策下的反应函数曲线，分别如图5、6所示。最优反应函数的斜率为负，这也反映出了线上渠道与线下渠道订货量存在着一定的替代关系，从而验证了定理1的存在性。另外，从图5、6中还可以看出反应曲线的交点变动不大，即订货纳什均衡对服务费用不敏感，其原因在于，随着线上渠道收取的服务费用的增加，线下渠道为了提高收益而增加订货量，此时会产生两种效应，一是线上渠道商由于预测线下渠道会增加订货量，于是为了增加收益也提高订货量；二是会进一步的通过提高服务费的收益而降低订货量。第二种效应虽然会大于第一种效应，但是在一定程度了却阻碍了线下渠道提高订货量的程度，因此导致了线下渠道订货对服务费用的敏感性。

图5 最优反应函数(τ=27)

图6 最优反应函数(τ=30)

5 结论

本文针对顾客转移导致的双渠道冲突问题， 以一个开辟线上渠道的制造商和一个线下渠道组成的双渠道供应链为研究对象，探讨了二者的订货与协调机制，并进一步研究交货期差异率如何影响订货等问题，其主要结论如下：

(1)在服务费用满足一定的条件下，线上渠道与线下渠道的订货存在唯一的纳什均衡，其原因在于二者订货量存在一定的替代关系；

(2)线上渠道与线下渠道订货量与交货期差异率分别存在单调非增与单调非减关系；

(3)设计了两部定价协调机制实现了线上渠道与线下渠道的双赢，为现实中开辟线上渠道的制造企业与线下渠道进行带竞争行为的合作提供了理论依据。

由于本文仅仅针对一个线下渠道去研究，在实践中往往存在多个线下渠道，而多个线下渠道之间往往存在一定的合作关系，从而会对开辟线上渠道的制造商产生直接与间接抵制作用影响，这也是下一步的研究方向。