政府补贴下闭环供应链回收渠道的选择策略
林贵华, 单仁邦, 陈拼博
(上海大学 管理学院,上海 200444)
0 引言
近年来,各级政府和企业在追求正向供应链效益的同时,也越来越重视废旧产品的回收再利用。伴随着低碳环保、绿色发展理念的提倡以及《废弃电器电子产品回收处理管理条例》的颁布,废旧品回收已然成为一种环保趋势。通过废旧产品的回收、拆解、有用零部件的提取等一系列流程来减少资源浪费,提高资源的重复利用率。我国废旧产品回收再利用正处于起步阶段,亟需政府参与,通过政府制定优惠或补助政策来激励相关企业参与废旧品回收,从而促进社会和国家的可持续健康发展。
众多学者研究了单一回收渠道供应链中不同主体负责回收的最优策略问题。其中,Savaskan等讨论了如何选择反向渠道回收废旧产品的问题,并通过研究以制造商为领导者的Stacklberg博弈,指出零售商负责回收是最好的选择[1]。魏洁和李军基于EPR约束建立并对比分析了EPR下的三种物流回收模型,结果表明产品回收模式相较于传统模式发生了根本性的变化[2]。Wei和Zhao建立了三种不同主体负责回收的博弈模型,对模糊闭环供应链中逆向渠道选择的决策问题进行了研究,并结合模糊理论分析了三种模式下策略的不同[3]。付小勇等在两个回收商回收价格竞争下,运用演化博弈对回收渠道的决策进行了分析,研究表明两个处理商都会选择直接回收方式进行回收[4]。聂佳佳和邓东方认为产品质量对回收存在影响,建立了制造商和零售商分别负责回收的闭环供应链模型,通过求解和对比分析,指出在一定条件下制造商和零售商会倾向于同一种回收模式[5]。付小勇等针对废旧电子产品回收市场中回收渠道选择的问题,构建了双链竞争下处理商回收渠道选择的博弈模型[6]。Shi等基于零售商、制造商和第三方物流服务提供商构成的再制造闭环供应链系统,构建了三种不同回收的再制造模式,通过分析三种模型的结果,指出不同主体的回收模式的选择是有所不同的[7]。舒秘和聂佳佳认为制造商存在产能约束,利用博弈模型研究了制造商的生产能力对回收渠道决策的影响,结果表明,当存在产能约束时,制造商回收渠道中的回收率总是最高的[8]。卢荣花和李南从电子产品本身特性出发,基于零售商竞争,建立了制造商回收和零售商回收的闭环供应链模型,并对均衡解进行了分析,给出了不同主体的最优回收渠道选择策略[9]。李晓静等基于供应链竞争,以集中决策下的结果为参照,分析了分散决策下不同回收渠道的均衡解,并从回收率和不同主体共赢角度讨论了最优回收渠道的选择[10]。Giri等基于线上线下同时销售产品,在五个不同的场景下,对供应链定价和产品回收决策进行了分析,结果表明,零售商负责回收比其他回收模式带来了更多的利润[11]。
近年来,随着废旧电器电子产品回收政策的颁布,多回收渠道供应链受到越来越多的重视,不少学者开始研究政府干预对回收渠道选择的影响。其中,熊中楷等对三种不同主体回收的模式进行了分析,通过引入政府奖励条件,对三种模式进行了深入研究和比较,并分析了政府奖励对不同主体回收的影响[12]。Ma等研究了消费补贴对双渠道闭环供应链的影响,分别分析了政府资助项目实施前后渠道成员的决策,并从消费者、供应链系统和企业角度考虑了消费补贴的影响[13]。安彤和周海云建立了政府干涉下制造商和零售商分别负责回收及混合回收的决策模型,基于求解结果,从消费者、政府、制造商、零售商和供应链整体五个角度研究了回收渠道的选择策略[14]。杨春苗和戴更新以零售商回收的闭环供应链为研究对象,首先对有无政府补贴下的最优解进行了比较,其次研究了政府补贴对零售商回收努力程度的影响[15]。Xie和Ma基于彩电双寡头市场,考虑了政府对回收商进行补贴时两个回收商和一个处理商之间的博弈关系[16]。Liu等以WEEE回收市场为研究对象,考虑了政府对正规部门的补贴情形下,在质量基础上正规部门回收和不正规部门回收的定价模型[17]。Heydari等考虑了由一个制造商和一个零售商组成的二级逆向供应链,分析了政府对供应链成员的不同激励机制(免税和补贴),研究结果表明,政府对制造商的激励优于零售商[18]。Gu等在市场需求不确定情况下,研究了政府补贴和电池回收下电动汽车制造商的最优生产策略,结果表明,补贴的增加可提高制造商的最佳生产量和预期效用[19]。赵敬华和林杰针对政府采取不同补贴对象策略的情况,分别建立了定价模型,并对比研究了不同补贴对象下的销售、回收渠道定价及利润,分析了不同补贴对象的影响系数对定价决策的影响[20]。程发新等基于废旧产品回收质量的不确定性,建立了政府差别补贴下的闭环供应链定价决策模型,对比分析了政府补贴第三方回收商和制造商的两种补贴方式,探讨了政府差别补贴和回收质量不确定对闭环供应链定价决策的影响[21]。胡强等以逆向供应链为研究对象,设计了政府与制造商及回收商之间的两种激励契约,分析了各相关参数对契约设计及企业选择的影响,并指出政府的激励契约对再制造产业的发展具有重要作用[22]。周蕊等建立了无政府参与、政府补贴和政府奖惩机制下的三种决策模型,对比分析不同机制的结果,研究表明补贴和奖惩机制均能起到激励作用,能够调动回收商的回收积极性[23]。Li等考虑了再制造供应链的两期竞争模型,在第二阶段中对竞争中有无政府补贴及税收进行研究,而该文的政府补贴是指对再制造产品进行补贴,通过研究表明政府补贴对制造商和再制造决策存在不对称影响[24]。Zhao等考虑了消费者对再制造产品的偏好和政府补贴的影响,研究发现,如果再制造商与消费者分享一定比例的补贴,则它可以因市场增加而获利更多[25]。Huang等研究了政府对节能产品的最优补贴,研究发现,如果补贴太低,低成本企业可能会生产未经认证的产品,而高成本企业则会生产认证产品[26]。
值得一提的是,上述有关政府因素的研究中,文献[14,20,21]讨论了政府对制造商的回收补贴;文献[15,18]则讨论了政府对零售商的补贴问题,并以一定的补贴系数作为研究基础;文献[13,16,17,22,24,25]分别对消费补贴、政府补贴正规非正规回收商和再制造商等问题进行了探索。然而,尚没有文献考虑政府对间接回收者的补贴、以及不同主体回收下政府补贴对决策者策略选择的影响。本文将政府这一角色融入闭环供应链系统中,在回收过程中给予不同主体一定的补贴扶持,即同时补贴间接回收和直接回收的主体。通过分析三种不同主体回收模式,从不同的决策主体角度,给出相应的回收渠道的选择建议,以期为闭环供应链实际的发展和有效运行提供参考。
1 问题描述
本文以单一制造商、零售商和第三方构成的闭环供应链系统为研究对象。在正向供应链中,制造商以单位生产成本cm生产新产品和单位生产成本cr对废旧产品进行再制造,并以批发价ω批发给零售商,零售商则以零售价p向消费者销售产品。在逆向供应链中,制造商直接对废旧产品进行回收,则政府给予制造商补贴。当制造商对废旧产品进行间接回收时,以不同的转移价格bR和bT从零售商或第三方处回收废旧产品。此时,政府不仅给予零售商或第三方(直接回收)补贴,还会对制造商(间接回收)进行补贴。如图1所示,其中实线表示正向供应链,虚线表示逆向供应链。
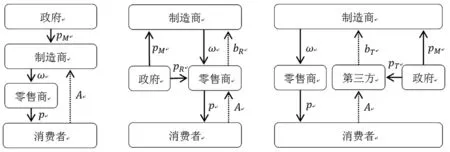
图1 模型结构图
1.1 符号定义
基于上述问题描述,本文将研究所涉及的变量和参数及上下标描述见表1。

表1 变量和参数含义说明
特别,bR表示制造商从零售商处回收废旧产品的转移价格,bT表示制造商从第三方处回收废旧产品的转移价格;pM表示政府对制造商单位回收产品的补贴,pR表示政府对零售商单位回收产品的补贴,pT表示政府对第三方单位回收产品的补贴。
1.2 基本假设
(1)再造品和新产品在质量、大小、外观等方面无明显差异。
(2)制造商、零售商及第三方保证信息共享,即信息对称。
(3)新产品的单位生产成本大于再造品的生产成本,即cm>cr>0。
(4)单位回收节约成本大于单位回收成本,即Δ>A>0。
(5)闭环供应链中所有成员均参与其中,并且有p>w>0。
(6) 制造商、零售商及第三方在回收上均有利可图,即Δ≥bR>A>0,Δ≥bT>A>0。
(7)市场需求为价格的线性函数,即q=φ-βp,其中β>0。
(8)期望回收率与回收投入的关系式为I=CLτ2(见文献[1]),其中0≤τ≤1。这意味着,期望回收率越高,回收投入越多。
2 回收模型的建立与求解
2.1 集中决策情形
(1)制造商的回收模型
在集中决策下,所有供应链成员被看作一个整体。供应链整体以总利润最大化为目标来决定零售价和期望回收率,其模型为
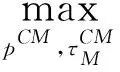
s.t.βpCM<φ
pCM>cm
(1)
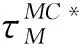
此时,最优利润函数值为
(2)零售商的回收模型
同上,供应链整体以总利润最大化为目标来决定零售价和期望回收率,其模型为
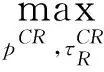
s.t.pCR>cm
βpCR<φ
(2)

此时,最优利润函数值为
(3)第三方的回收模型
同上,供应链整体以总利润最大化为目标来决定零售价和期望回收率,其模型为
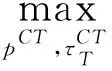
s.t.pCT>cm
βpCT<φ
(3)

此时,最优利润函数值为
2.2 分散决策情形
(1)制造商的回收模型
在分散决策下,制造商和零售商都是独立决策者,且均追求自身利润最大化。假设Stackelberg博弈发生在制造商和零售商之间,其中制造商作为Stackelberg领导者L主导供应链系统,而零售商是追随者F1。零售商与制造商的最优决策模型分别为

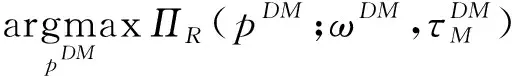
ωDM≥cm
(4)
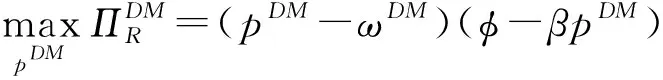
s.t.pDM>ωDM
βpDM<φ
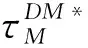
此时,各自的最优利润函数值分别为
(2)零售商的回收模型
同上,零售商与制造商的最优决策模型分别为
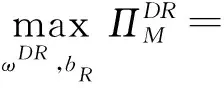

ωDR≥cm
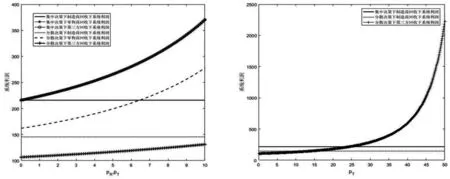
A (5) s.t.pDR>ωDR βpDR<φ 此时,各自的最优利润函数值分别为 (3)第三方的回收模型 假设Stackelberg博弈发生在制造商和其他代理商之间,其中制造商作为Stackelberg领导者L主导供应链系统,而零售商和第三方则是追随者F1,F2。三者的最优决策模型分别为 ωDT≥cm A (6) s.t.pDT>ωDT βpDT<φ 此时,各自的最优利润函数值分别为 基于2.1和2.2小节集中决策和分散决策的结果,分别比较零售价、期望回收率和系统利润的大小关系,可得到如下结论。 证明同上,此处省略该比较证明。 证明同上,此处省略该比较证明。 当满足条件4CL>β(Δ-A+pM+pR)2和4CL>β(Δ-A+pM+pT)2时,对三种不同回收渠道下的最优策略进行比较,见表2。 表2 集中决策下不同主体回收的最优策略 为简便起见,在下述命题中,令t=Δ-A+pM。 命题7已知集中决策下制造商回收、零售商回收和第三方回收的最优期望回收率,当政府对零售商的回收补贴大于政府对第三方的回收补贴时,零售商回收下的最优期望回收率更高;反之,第三方回收下的最优期望回收率更高。双回收(零售商或第三方直接回收,制造商间接回收)补贴下的最优期望回收率明显优于单回收(制造商直接回收)补贴下的最优期望回收率。即制造商回收、零售商回收和第三方回收下的最优期望回收率之间的关系为: 命题8已知集中决策下制造商回收、零售商回收和第三方回收的最优零售价,当政府对零售商的回收补贴大于政府对第三方的回收补贴时,第三方回收下的最优零售价更高;反之,零售商回收下的最优零售价更高。双回收(零售商或第三方直接回收,制造商间接回收)补贴下的最优期望回收率明显劣于单回收(制造商直接回收)补贴下的最优零售价。即制造商回收、零售商回收和第三方回收下的最优零售价之间的关系为: (1)若pR>pT,则pCR* (2)若pR=pT,则pCT*=pCR* (3)若pR 命题9已知集中决策下制造商回收、零售商回收和第三方回收的最优期望回收率,当政府对零售商的回收补贴大于政府对第三方的回收补贴时,零售商回收下的系统利润更高;反之,第三方回收下的系统利润更高。双回收(零售商或第三方直接回收,制造商间接回收)补贴下的系统利润明显优于单回收(制造商直接回收)补贴下的系统利润。即制造商回收、零售商回收和第三方回收下的系统利润之间的关系为: 当4CL>β(Δ-A+pM+pR)2和4CL>β(Δ-A+pM+pT)2时,对三种不同回收渠道下的最优策略进行比较,见表3。 表3 分散决策下不同主体回收的最优策略 为简便起见,在下述命题中,令t=Δ-A+pM。 (1)若pT>2pR+t,则pDT* (2)若pT=2pR+t,则pDT*=pDR* 本节运用Matlab软件分析集中决策和分散决策情形下政府补贴对不同主体回收渠道的零售价、期望回收率、系统利润等方面的影响,并从不同主体角度分析回收渠道的策略选择。以下假定CL=800,φ=100,β=2,cm=32,Δ=30,A=15,pM=5 。 由第2节知,零售商回收和第三方回收下的最优期望回收率分别是关于政府补贴pR和pT的函数,且随着政府补贴的增加而增加,亦即政府补贴越多期望回收率越高。如图2所示,在集中决策下,零售商回收和第三方回收下的期望回收率明显高于制造商回收下的期望回收率。在这种情形下,政府会偏向于选择零售商或第三方进行废旧产品回收。当政府对零售商回收的补贴小于政府对第三方回收的补贴,即pR 图2 期望回收率与政府补贴的关系 在集中决策下,零售价与政府补贴之间的关系如图3所示。从图中容易看出,制造商回收下的零售价明显高于零售商和第三方回收下的零售价,且零售商和第三方回收下的零售价随着政府补贴的增加呈现下降趋势。此时,对于消费者而言,零售价越低越好,故消费者会偏向于选择零售商回收或第三方回收下购买商品。当政府对零售商回收的补贴小于政府对第三方回收的补贴,即pR 图3 零售价与政府补贴的关系 在分散决策下,受政府补贴pR的影响,如图3左图所示,当政府补贴pR和pT皆小于8.28时,第三方回收下的零售价明显高于制造商和零售商回收下的零售价。而不论pR如何变化,零售商回收下的零售价始终小于制造商回收下的零售价,即pDT*>pDM*>pDR*,此时消费者会选择在零售商回收下购买商品。当8.28 在集中决策下,图4描述了系统利润和政府补贴的关系。由此图可知,零售商和第三方回收下的系统利润随着政府补贴的增加而增加,且制造商回收下的系统利润明显低于零售商和第三方回收下的系统利润,即对于政策制定者而言,选择零售商或第三方对废旧产品进行回收才是更为明智的选择。当政府对零售商回收的补贴小于政府对第三方回收的补贴,即pR 图4 系统利润与政府补贴的关系 本文主要针对单一制造商、零售商和第三方构成的闭环供应链系统,讨论了政府对直接回收和间接回收的补贴政策,比较分析了不同主体回收下的最优策略,并分析了政府补贴对不同回收主体下的最优策略的影响。同时,从不同的决策主体角度,分析了回收渠道的选择策略。研究结果表明,在集中决策和分散决策下,当三种不同主体回收同时存在时,若政府补贴越少,则政府、消费者和政策制定者越会倾向于选择零售商对废旧产品进行回收;反之,则政府、消费者和政策制定者会选择第三方对废旧产品进行回收。 未来,结合政府角色的闭环供应链回收渠道策略选择的研究可以从单回收渠道延伸到混合回收渠道。此外,可尝试用非线性需求函数替代线性需求函数,亦可考虑随机因素对需求的影响,进而对回收渠道进行深入研究。
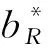
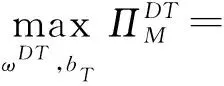
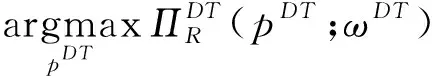
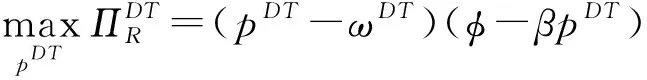

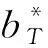
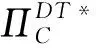
2.3 集中与分散结果对比

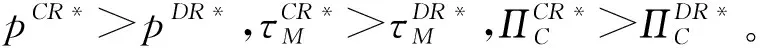
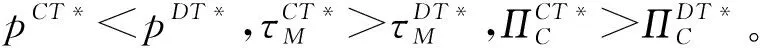
3 对比分析
3.1 集中决策情形


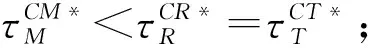
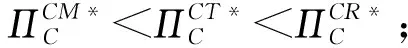
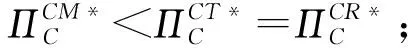
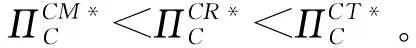
3.2 分散决策情形

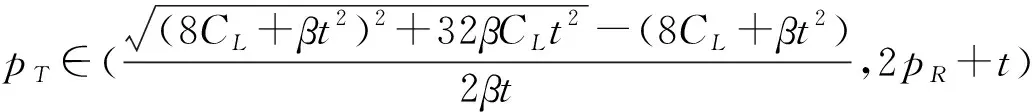
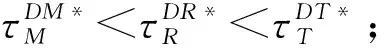
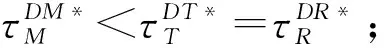
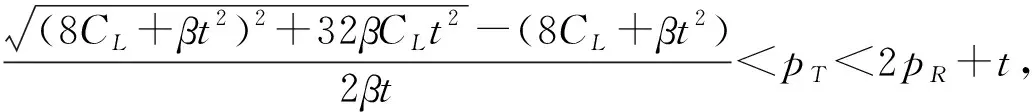
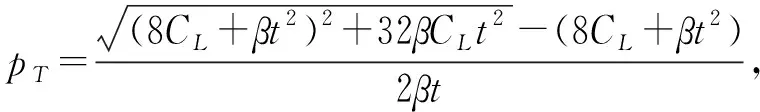
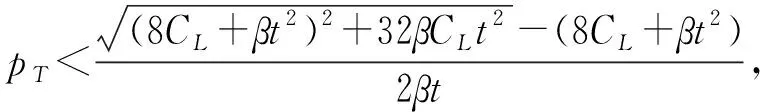
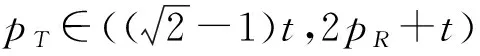
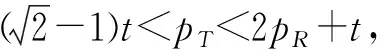
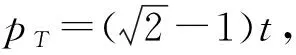

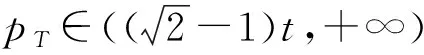
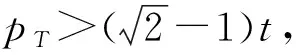
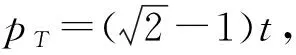

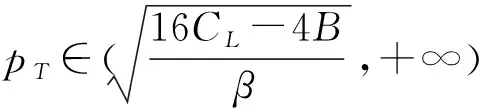
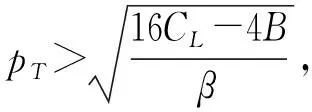

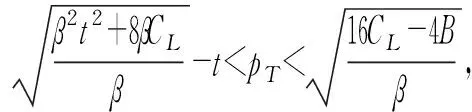
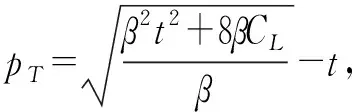
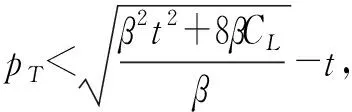
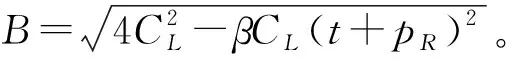
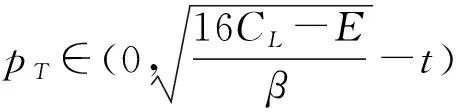
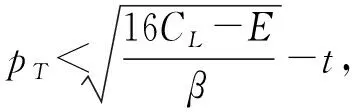

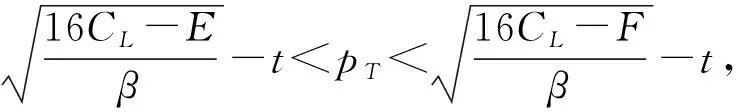
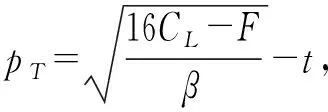

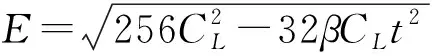
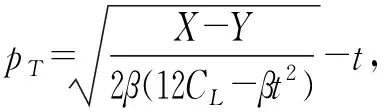
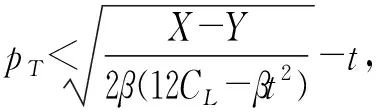

4 数值分析
4.1 从政府角度选择回收渠道的策略
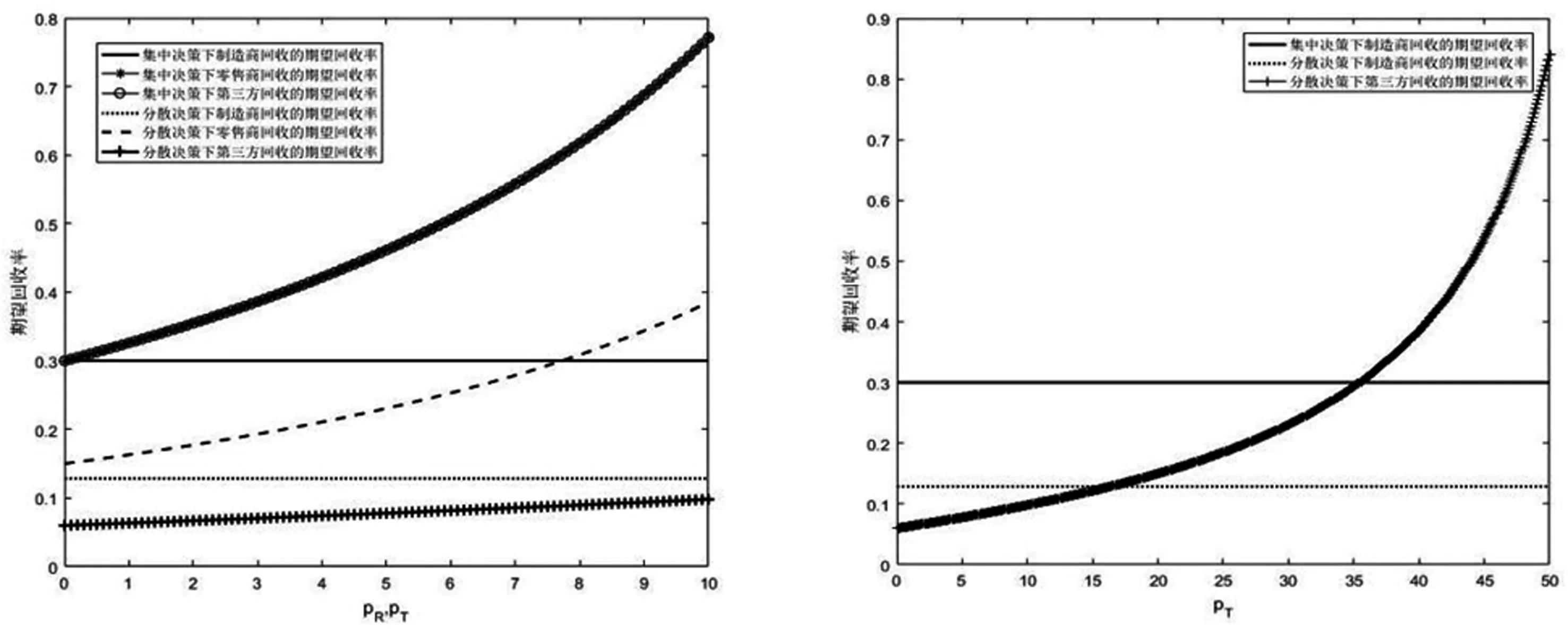
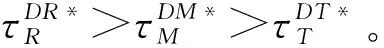
4.2 从消费者角度选择回收渠道的策略

4.3 从政策制定者角度选择回收渠道的策略
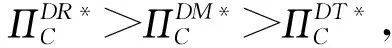
5 结论

