基于Ansys Workbench的螺栓连接模拟方法对比分析
杨应坡,冀永曼
(1.许昌电气职业学院,河南 许昌461000;2.新乡职业技术学院,河南 新乡453000)
螺栓作为标准件,连接简单可靠、价格低廉,是大型装配体中最为常见的一种连接形式,广泛应用于各类复杂的机械结构中.螺栓连接的详细仿真模型,一方面几何建模较复杂,另一方面网格划分、模型前处理也较困难,分析计算的成本也会较高[1-4].因此,关注螺纹或者需要很精细的考虑螺栓表面的应力分布、接触状态、疲劳特性时,才会使用真实螺栓几何模型[1-4].
螺栓连接主要用来传递力和力矩.大型装配体中包含的螺栓数目可能达到几十个、几百个甚至更多,相对被连接结构,螺栓尺寸较小.仿真计算工程应用中,综合考虑模型规模、计算效率、仿真精度、收敛调试难度等方面的因素,使用真实的螺栓几何模型的场合较少.零件数量多,准确的几何细节和精细的网格模型,可能导致计算模型的规模大,而实际取得的精度提升及其有限,所以螺栓的模型简化往往是必需的[5-7].常用的结构仿真软件,如Ansys[2]、NASTRAN[8]、HyperMesh[9]都有相应的针对螺栓连接的模拟.针对不同的应用场合,不同的模拟方法[9-13],虽然都有相应的研究,但是很少有文章能够全面研究不同的模拟方法的特点,以及不同接触方式、受力位置的情况之间的差异.所以针对具体的应用场合,选择何种模拟方法、接触方式、受力位置来进行螺栓连接的模拟,还需要进行进一步的仿真计算对比,本文基于Ansys Workbench软件对各种不同螺栓模拟方法进行对比.
1 装配体几何模型
进行仿真计算的装配体几何模型如图1所示,为两块平板,中间采用两个螺栓连接,其中一块平板的端面固定支撑.平板尺寸为200 mm×40 mm×5 mm,采用M6螺栓连接,连接处的通孔为Φ6.5 mm,螺栓头或螺母的端面和平板的接触圆直径约为10 mm,也即是相应的垫片接触直径.平板和螺栓均使用软件默认的Structural Steel材料.对应的坐标系如图中所示,X轴沿平板的长轴方向,Z轴沿平板厚度方向.

图1 装配体几何模型Fig.1 Assembly geometric model
根据不同接触方式、受力位置的情况,进行仿真分析的常用受力位置如图2所示,分别为螺栓接触面,通孔柱面,通孔边线.常见的方式为螺栓接触面,也就是垫片的接触区域;通孔柱面和通孔边线往往在过渡配合、承受剪切作用才会在此区域受力.
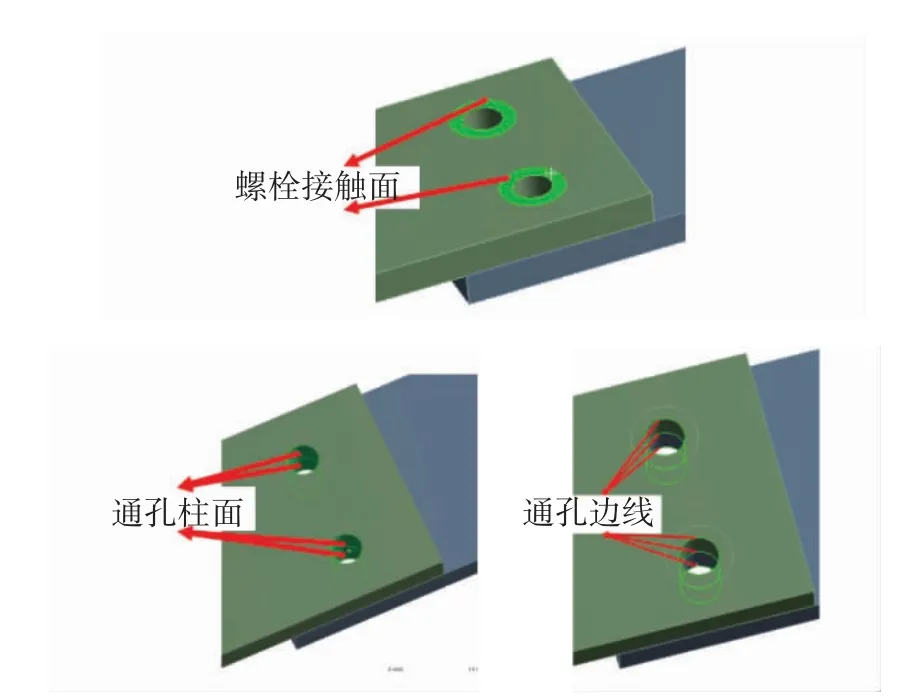
图2 螺栓连接的不同受力位置Fig.2 Different forced position of bolt connection
2 有限元前处理
划分网格后的模型如图3所示,对左边平板的侧面采用固定约束.

图3 装配体的有限元网格模型Fig.3 Finite element mesh model of assembly
分别对螺栓连接采用以下方式进行模拟:(1)螺栓模型去螺纹实体模型,进行连接模拟;(2)螺栓使用圆柱简化,进行连接模拟;(3)螺栓使用线体简化,进行连接模拟;(4)螺栓使用Beam单元简化,进行连接模拟;(5)螺栓连接使用关节连接简化模拟.真实的螺栓模型[1,3],以及通过Ansys软件接触→几何修正→螺纹接触,可以不建立螺纹模型但是可以模拟螺纹接触的应力分布[10,13],这两种方式很少用于大型装配体,本文不再进行详细讨论.
每种模拟方法,根据接触或者受力位置的不同,进行模态分析对比.主要对比前六阶振动振型和固有频率,分别从模型规模、计算效率、仿真精度的角度,对各模拟方法的结果进行评估.
3 不同模拟方法的仿真分析
对图1所示螺栓连接的装配体应用上述五种模拟方法,进行模态分析和固有频率的计算.各种模拟方法得到的振型是一致的,只是固有频率的值存在一定的差异.
该装配体的各阶振型如图4所示,一阶振型为沿Z向的一阶振动;二阶振型为沿Z向的二阶振动;三阶振型为绕Z轴转动的振动;四阶振型为绕X轴转动的振动;五阶振型为沿Z向的三阶振动;六阶振型为沿Z向的四阶振动.

图4 螺栓连接装配体各阶振型Fig.4 Vibration modes of bolt connection assembly
3.1 螺栓模型去螺纹实体模型
该模拟方法中,针对螺栓接触面力的传递方式采用Bonded接触对和接触面节点合并(Node Merge),进行仿真分析.去掉螺纹,螺栓头和螺母均简化成圆柱状,如图5所示.
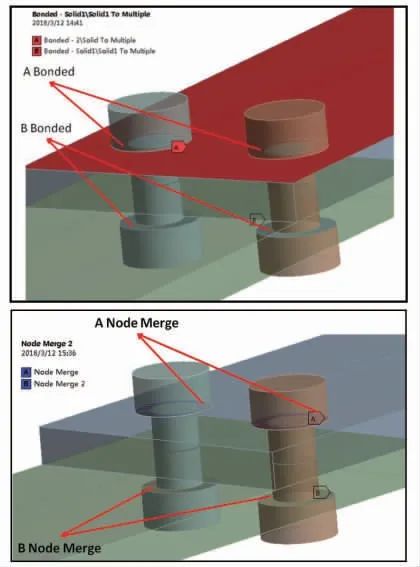
图5 螺栓去螺纹实体装配体模型Fig.5 Solid assembly model of bolt without thread
Bonded接触对形式不要接触面上的网格一致,而进行节点合并,接触面网格一致.
3.2 螺栓使用实体圆柱简化
螺栓和螺母仅用和螺杆外径相同的圆柱体简化(如果关注螺栓的强度或者应力分析,还需考虑外径、中径、内径的差异),如图6所示.该模拟方法中,针对螺栓接触面力的传递方式采用Bonded接触对和接触面节点合并,进行仿真分析.

图6 实体圆柱简化螺栓的装配体模型Fig.6 Assembly model of a solid cylindrical simplified bolt
3.3 螺栓使用线体简化
如图7所示,将螺栓简化为截面为6 mm直径圆的线体,线体的两个端点分别和其邻近的螺栓接触面添加bonded接触,接触区域半径5 mm,刚好覆盖螺栓接触面的区域.接触算法分别选择Beam和MPC进行对比.

图7 螺栓使用线体简化的装配体模型Fig.7 Simplified assembly model of bolt using line body
3.4 Beam单元模拟螺栓连接
如图8所示,在每对螺栓孔的圆柱面之间添加Body-Body-->Beam连接,来对螺栓连接进行模拟,分别选择使用通孔柱面连接、通孔边线连接、螺栓接触面连接来进行受力的传递.有限元模型及其连接关系如下图所示.
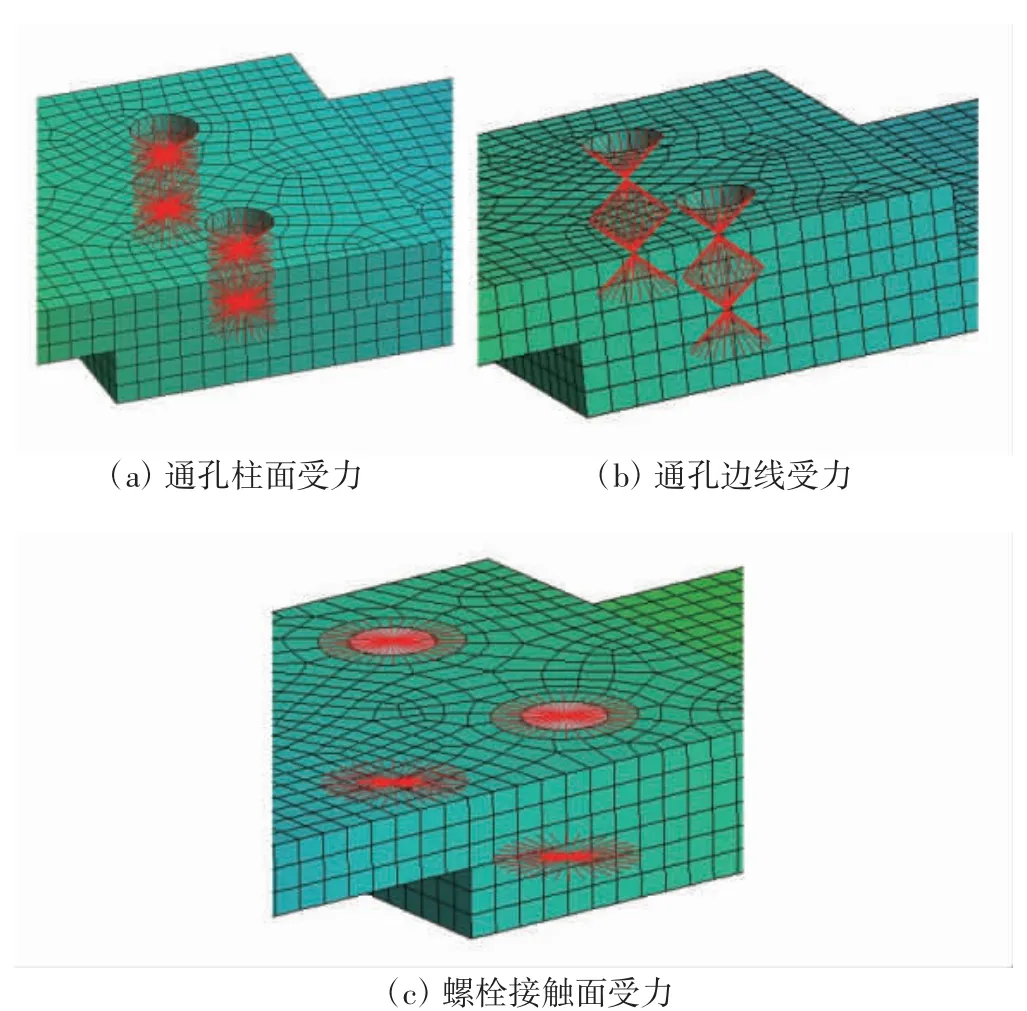
图8 螺栓使用线体简化的有限元模型Fig.8 Simplified finite element model of bolt using line body
图8可以看出,不同的受力面连接,最终体现在和线体连接的节点不同,也就是力的传递路径有差异.
3.5 关节连接模拟螺栓连接
如图9所示,在每对通孔柱面之间添加Body-Body-->Fixed关节连接,来对螺栓连接进行模拟,分别选择使用通孔柱面连接、通孔边线连接、螺栓接触面连接来进行受力的传递.几何模型、有限元模型及其连接关系如图9所示.

图9 关节连接模拟螺栓连接图Fig.9 Joint connection simulation bolt connection
4 结果对比
上文中,对5种螺栓连接模拟方法,以及不同接触方式、受力位置的情况进行了仿真计算,下面从模型规模、计算效率、仿真精度的角度,对各模拟方法的结果进行评估,如表1所示.
表中的最大相对误差,以螺栓模型去螺纹实体模型Bonded接触为基准,进行相对误差的计算.当螺栓较多,模型规模大时,单元数量和计算时间的差异将比上表中要大得多,对实际计算的影响将会很大.
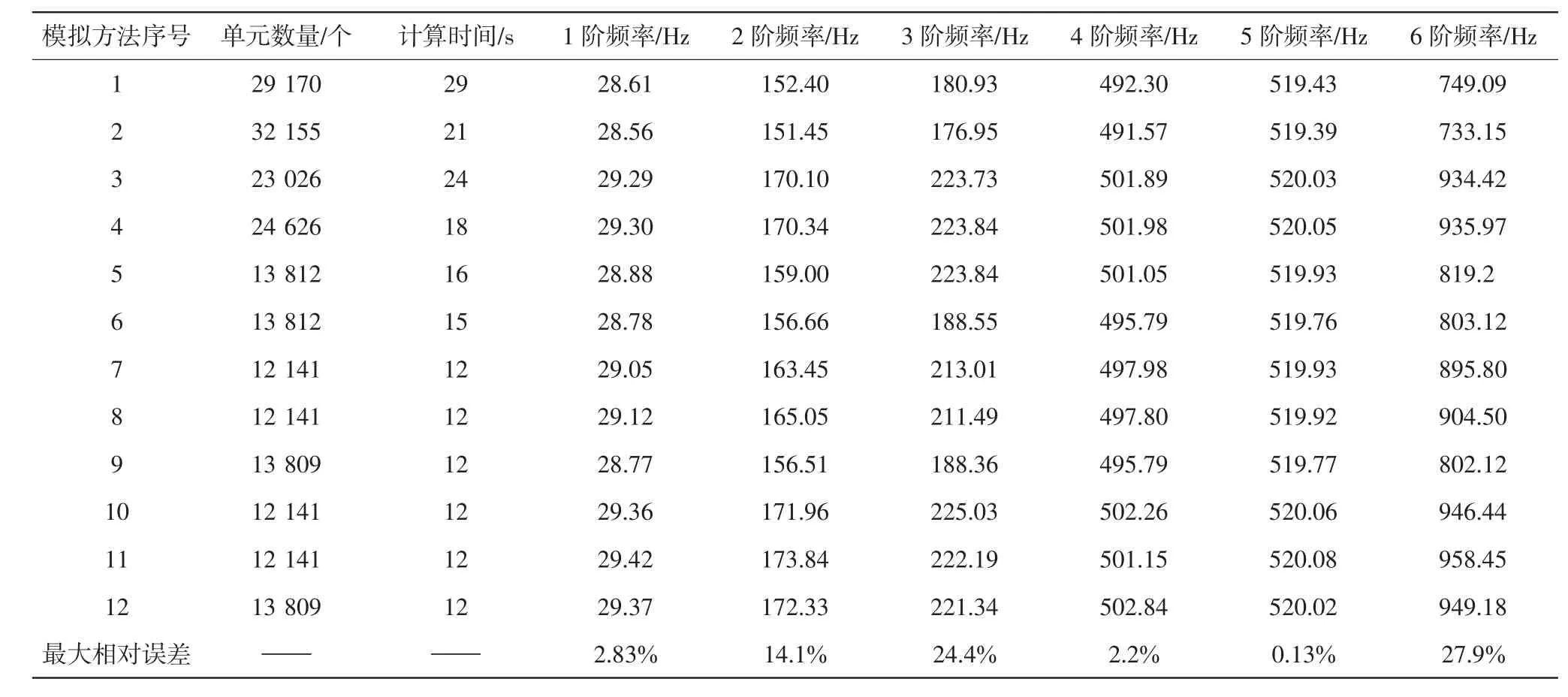
表1 各模拟方法的仿真计算结果Tab.1 Simulation calculation results of various simulation methods
其中,模拟方法序号分别表示如下:1为螺栓模型去螺纹实体模型,Bonded接触;2为螺栓模型去螺纹实体模型,接触面节点合并;3为螺栓实体圆柱简化,Bonded接触;4为螺栓实体圆柱简化,接触面节点合并;5为螺栓线体简化,接触算法分Beam;6为螺栓线体简化,接触算法MPC;7为Beam单元模拟,通孔柱面受力;8为Beam单元模拟,通孔边线受力;9为Beam单元模拟,螺栓接触面受力;10为关节连接模拟,通孔柱面受力;11为关节连接模拟,通孔边线受力;12为关节连接模拟,螺栓接触面受力.
5 结论
分别对螺栓连接采用5种模拟方法进行仿真计算,得到以下结论:
1)从表1可以看到,螺栓采用实体模型,网格规模要大多,尤其是螺栓较多时,网格规模增大显著得多,而网格规模直接决定了计算效率.
2)通过表中模拟方法序号1和2、3和4的对比可以发现,网格规模相当的情况下,采用接触对处理比节点合并的计算效率要低,接触对很多时将表现更为明显.
3)共振时,螺栓连接的位置位移较大时,不同模拟方法的固有频率数值差异较大.其中一、四、五阶不同模拟方法的相对误差明显要小.
4)螺栓使用线体简化和Beam单元简化,螺栓接触面为受力面,计算得到的固有频率误差较小,更符合实际的受力情况.
5)线体简化和Beam单元简化,螺栓接触面为受力面,可以减小有限元模型规模、提高计算效率、仿真精度较高,各阶固有频率相对误差均在10%以内,更适用于大型复杂装配体的螺栓连接模拟.

